Volume 2014, Issue 1 159198

Research Article

Open Access

Stabilization with Internal Loop for Infinite-Dimensional Discrete Time-Varying Systems

Nai-feng Gan,

Corresponding Author

Nai-feng Gan

[email protected]

School of Mathematical Sciences, Dalian University of Technology, Dalian 116027, China dlut.edu.cn

College of Mathematics and Information Science, Anshan Normal University, Anshan 114007, China asnc.edu.cn

Search for more papers by this author

Yu-feng LU,

Yu-feng LU

School of Mathematical Sciences, Dalian University of Technology, Dalian 116027, China dlut.edu.cn

Search for more papers by this author

Ting Gong,

Ting Gong

School of Mathematical Sciences, Dalian University of Technology, Dalian 116027, China dlut.edu.cn

Search for more papers by this author

Nai-feng Gan,

Corresponding Author

Nai-feng Gan

[email protected]

School of Mathematical Sciences, Dalian University of Technology, Dalian 116027, China dlut.edu.cn

College of Mathematics and Information Science, Anshan Normal University, Anshan 114007, China asnc.edu.cn

Search for more papers by this author

Yu-feng LU,

Yu-feng LU

School of Mathematical Sciences, Dalian University of Technology, Dalian 116027, China dlut.edu.cn

Search for more papers by this author

Ting Gong,

Ting Gong

School of Mathematical Sciences, Dalian University of Technology, Dalian 116027, China dlut.edu.cn

Search for more papers by this author

First published: 28 April 2014

https://doi.org/10.1155/2014/159198

Citations: 1

Academic Editor: Manuel De la Sen

Share a link

Email
Wechat
Bluesky

Abstract

The concepts of stabilization with internal loop are analyzed for well-posed transfer functions. We obtain some sufficient and necessary conditions such that a stabilizing controller with internal loop stabilizes plant L. We also analyze two special subclasses of stabilizing controllers with internal loop, called canonical and dual canonical controllers, and show that all stabilizing controllers can be parameterized by a doubly coprime factorization of the original transfer function.

1. Introduction

Control Theory is a relevant field from the mathematical theoretical point of view as well as in many applications (see [1–6]). What is important, in particular, is the closed-loop stabilization of dynamic system under appropriate feedback control as a minimum requirement to design a well-posed feedback system. In the last twenty years, the closed-loop system whose stability is achieved by the controller with internal loop has attracted the attention of many authors (see [7, 8]). While extending the theory of dynamic stabilization to regular linear systems (a subclass of the well-posed linear systems), it was shown in [7, Example 2.3] that even the standard observer-based controller is not a well-posed linear system and its transfer function is not well-posed. To overcome this, paper [8] proposed another definition of a stabilizing controller which is more general than that has been defined earlier, the so-called stabilizing controller with internal loop. The concept enabled a simple Youla parameterization and has some advantages which turn out to be very important for infinite-dimensional systems. It makes the theory of dynamic stabilization simpler and more natural [8].

Recently, the study of time-varying systems using modern mathematical methods has come into its own. This is a scientific necessity. After all, many common physical systems are time varying (see [9–14]). Paper [15] studied the concept of stabilization with internal loop for infinite-dimensional discrete time-varying systems and gave a parameterization of all stabilizing controllers with internal loop if I − K₂₂ has a well-posed inverse in the framework of nest algebra. But in many cases, the controller C = K₁₁ + K₁₂(I − K₂₂) ⁻¹K₂₁ will not be well-posed, but C perhaps stabilizes L.

In this paper, we study the stabilization with internal loop for the linear time-varying system under the framework of nest algebra. We extend our study of controllers with internal loop to more general use and give a parameterization of all stabilizing controllers with internal loop even if I − K₂₂ = 0. It is found that the stabilization with internal loop for the linear time-varying system obtained in [15] can be viewed as a special case of that obtained here. As we know, if the plant is not strictly proper, it is difficult to choose the parameter in such way that the resulting controller will be well-posed. Even if we choose to ignore well-posedness, we still have to ensure that the denominator in the Youla parameterization is invertible. This makes it awkward to use this parameterization to solve the practical problems, while the controller with internal loop overcomes this awkwardness. We obtain canonical and dual canonical controllers and show that all stabilizing controllers can be parameterized by a doubly coprime factorization of the original transfer function.

The rest of this paper is organized as follows. Mathematical background material and notation are introduced in Section 2. In Section 3, we give some sufficient and necessary conditions that a stabilizing controller with internal loop stabilizes plant L. In Section 4, we introduce canonical and dual canonical controllers. We show that a plant L is stabilizable with internal loop by a canonical (dual canonical) controller if and only if L has a right coprime (left coprime) factorization. We give a complete parameterization of all (dual) canonical stabilizing controllers with internal loop. Some conclusions are drawn in Section 5.

2. Preliminaries

We denote by ℤ₊ the nonnegative integers and by ℂ the complex numbers. Let H be the complex infinite-dimensional Hilbert sequence space:

()

where |·| denotes the standard Euclidean norm on ℂ. H_e will denote the extended space:

()

Definition 1 (see [3].)A family N of closed subspaces of the Hilbert space H is a complete nest if

(1)
{0}, H ∈ N.
(2)
For N₁, N₂, either N₁⊆N₂ or N₂⊆N₁.
(3)
If {N_α} is a subfamily in N, then ∩_αN_α and ∨_αN_α are also in N.

Every subspace N of H is identifiable with the orthogonal projection P_n

()

Properties (1) to (3) can be reformulated as follows.

(1^′) 0, I ∈ N.
(2^′) For P₁, P₂ ∈ N, either P₁ ≤ P₂ or P₂ ≤ P₁.
(3^′) If {P_α} is a nest in N which converges weakly (equivalently, strongly) to P, then P ∈ N.

Definition 2 (see [3].)If N is a nest and P is its associated family of orthogonal projections,

()

is called a nest algebra, where £(H) is the algebra of all bounded linear operators on H.

A linear transformation T on H_e is causal if P_nT = P_nTP_n for n ≥ 0.

Lemma 3 (see [3].)The following are equivalent:

(1)
T on H_e is stable.
(2)
T is causal and T∣H is a bound operator.
(3)
T is the extension to H_e of an operator in AlgR.

This lemma allow us to identify the algebra S of stable operators on H_e with the nest algebra AlgR. The restriction of T ∈ S to H is in AlgR and the extension of S ∈ AlgR to H_e is in S. AlgR and S are identical.

For L, K ∈ £, the operator matrix defined on H_e ⊕ H_e is called the feedback system with plant L and compensator K.

In Figure 1, L represents a given plant (system) and a compensator or controller; e₁, e₂ denote the externally applied inputs; u_L, u_K denote the inputs to the plant and compensator, respectively; and y_L, y_K denote the outputs of the compensator and plant, respectively.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The standard feedback system.

The closed-loop system equation are

()

The system is well-posed if the internal input u can be expressed as a causal function of the external input e. This is equivalent to requiring that

be invertible. The inverse is easily computed formally and is given by the matrix as follows:

()

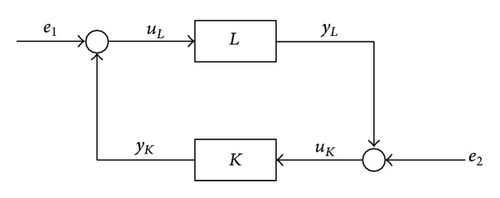
The closed-loop system {L, K} is stable if has a bound causal inverse defined on H ⊕ H. The stability of the closed-loop system is equivalent to requiring that the four elements of the 2 × 2 matrix H(L, K) be in S. L ∈ £ is stabilizable if there exists K ∈ £ such that {L, K} is stable.

3. Stabilization with Internal Loop

In this section, a new type of controller is introduced, the so-called stabilizing controller with internal loop; see [16–18].

The intuitive interpretation of Figure 2 is as follows: L represents the plant and K is the transfer function of the controller from to , when all the connections are open. The connection from ξ₀ to ξ_i is the so-called internal loop.

Partitioning K into

where K_ij ∈ £, i, j = 1,2, …,

()

is the transfer function of the closed-loop system from

Suppose I − K₂₂ is invertible in £; a parameterization of all stabilizing controllers with internal loop is given in [15]. If I − K₂₂ has a well-posed inverse, the internal loop can be closed first and the transfer function from y_k to u_k is

()

But in many cases, the expression (8) is not defined at all (this can happen if I − K₂₂ is nowhere invertible).

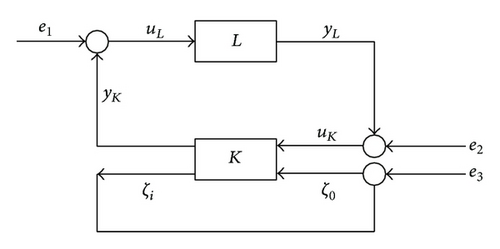
Example 4. Suppose L = I,

()

It is easy to see that the transfer function (8) of the controller is undefined since I − K₂₂ = 0. It is not difficult to check that K stabilizes L with internal loop (this verification can be simplified considerably by using Lemma 10).

In the following, we give some sufficient and necessary conditions such that a stabilizing controller with internal loop stabilizes plant L avoiding the condition that I − K₂₂ is invertible.

Theorem 5. Suppose that K₁₁ is an admissible feedback transfer function for L. Then F(K, L) has a well-posed inverse if and only if I − M is invertible in £, where M = K₂₂ + K₂₁L(I − K₁₁L) ⁻¹K₁₂.

Proof. Consider the following

()

where

, S₂₂ = I − K₂₂,

Since is invertible in M₂(£), thus is invertible in M₃(£) if and only if

()

is invertible in £.

Further, the condition that F(K, L) has a well-posed inverse is equivalent to that K is an admissible feedback transfer function with internal loop for L [7], so we have the following result.

Theorem 6. Suppose that K₁₁ is a stabilizing controller for L; then is a stabilizing controller with internal loop for L if and only if

(i)
(I − M) ⁻¹ ∈ S, where M = K₂₂ + K₂₁L(I − K₁₁L) ⁻¹K₁₂,
(ii)
there exist E₁, E₂ ∈ S such that LE₁ ∈ S, E₂L ∈ S, E₁(I − M)E₂L ∈ S, E₁(I − M)E₂ ∈ S, LE₁(I − M)E₂ ∈ S, LE₁(I − M)E₂L ∈ S,
(iii)
K₁₂ = (I − K₁₁L)E₁(I − M),
(iv)
K₂₁ = (I − M)E₂(I − LK₁₁).

Proof. K₁₁ stabilizes L if and only if .

If there exist E₁, E₂ ∈ S that satisfy (i)–(iv), all components in H(L, K) = F(K, L) ⁻¹ are

()

Thus, H(L, K) ∈ M₃(S), {L, K} is stable.

Conversely, H(L, K) = F(K, L) ⁻¹, and all components are

()

where M = K₂₂ + K₂₁L(I − K₁₁L) ⁻¹K₁₂. If H(L, K) ∈ M₃(S), then (I − M) ⁻¹ ∈ S. Let (I − K₁₁L) ⁻¹K₁₂(I − M) ⁻¹ = E₁ ∈ S, (I − M) ⁻¹K₂₁(I − LK₁₁) ⁻¹ = E₂ ∈ S; then K₁₂ = (I − K₁₁L)E₁(I − M), K₂₁ = (I − M)E₂(I − LK₁₁). From (3,1) ∈ S and (2,3) ∈ S, we have E₂L ∈ S and LE₁ ∈ S. Consider (1,1) ∈ S, (1,2) ∈ S, (2,1) ∈ S, (2,2) ∈ S, and {L, K₁₁} are stable; thus all other conditions in (ii) hold.

Remark 7. {L, K₁₁} stable is only sufficient condition for {L, K} stable, but not a necessary condition.

Theorem 8. If K₁₁ is an admissible controller for P, then {L, K} is stable if and only if

(i)
Δ⁻¹ = [I − K₂₂ − K₂₁L(I − K₁₁L) ⁻¹K₁₂] ⁻¹ ∈ S,
(ii)
A = (I − K₁₁L) ⁻¹K₁₂Δ⁻¹K₂₁(I − LK₁₁) ⁻¹ + K₁₁(I − LK₁₁) ⁻¹ = (I − K₁₁L) ⁻¹(K₁₂Δ⁻¹K₂₁ + K₁₁ − K₁₁LK₁₁)(I − LK₁₁) ⁻¹ ∈ S,
(iii)
AL ∈ S, LA ∈ S, LAL + L ∈ S, K₂₁(I − LK₁₁) ⁻¹L ∈ S, L(I − K₁₁L) ⁻¹K₁₂ ∈ S, K₂₁(I − LK₁₁) ⁻¹ ∈ S, (I − K₁₁L) ⁻¹K₁₂ ∈ S.

In fact, the conditions of Theorem 8 are weaker than those of Theorem 6. From the proof of Theorem 6, it is easy to obtain the result of Theorem 8.

We extend the plant , and L and C are parallel connection. as a feedback operator of G, so we have the following result.

Theorem 9. K is a stabilizing controller with internal loop for L if and only if I − FG is invertible in M₃(S).

Proof. F is a stabilizing controller for G if and only if

()

If (I − FG) ⁻¹ ∈ M₃(S), then F(I − GF) ⁻¹ = (I − FG) ⁻¹F ∈ M₃(S). Since (I − GF) ⁻¹ = I + G(I − FG) ⁻¹F, thus we only need to prove G(I − FG) ⁻¹ ∈ M₃(S). Consider F² = I; thus G(I − FG) ⁻¹ = F²G(I − FG) ⁻¹ = F[FG(I − FG) ⁻¹] = F[(I − FG) ⁻¹ − (I − FG)(I − FG) ⁻¹] = F(I − FG) ⁻¹ − F. If (I − FG) ⁻¹ ∈ M₃(S), then G(I − FG) ⁻¹ ∈ M₃(S).

Conversely, it is obvious.

4. Canonical and Dual Canonical Controllers

Another motivation for introducing controllers with internal loop is to obtain Youla parameterization. If the plant is not strictly proper, it is difficult to choose the parameter in such way that the resulting controller will be well-posed. Even if we choose to ignore well-posedness, we still have to ensure that the denominator in the Youla parameterization is invertible. By contrast, we can obtain a parameterization for all stabilizing canonical or dual canonical controllers.

The transfer functions of the controllers obtained there were of the form

()

We call the controllers of form (15) canonical controllers. Analogously, controllers of the form

()

will be called dual canonical controllers.

In following, we analyze the properties of (dual) canonical controllers in some detail. First, we recall Lemma 10 from [15].

Lemma 10 (see [15].)The canonical controller stabilizes L ∈ £ with internal loop if and only if

()

is invertible in S and LΔ⁻¹ ∈ S.

If L ∈ £ has a right-coprime factorization L = NM⁻¹, then K stabilizes L with internal loop if and only if

()

is invertible in S.

We now turn to the problem of simultaneous stabilization. Given L₀ ∈ S and L₁ ∈ £, the following Corollaries 11 and 12 give the conditions that L₁ − L₀ can be stabilized by some canonical controller.

Corollary 11. If L₀ ∈ S and L₁ ∈ £ can be simultaneously stabilized by canonical controller , then L₁ − L₀ can be strongly stabilized by some canonical controller.

Proof. If is a strong right representation of L₁, then is a strong right representation of L₁ − L₀, since

()

for L₀ ∈ S.

Suppose stabilizes L₁ − L₀; then by Lemma 10,

()

is invertible in S. By Lemma 10, Δ and D are invertible in S:

()

Define

()

Thus D^′ is invertible in S, and

stabilizes L₁ − L₀.

Corollary 12. Suppose L₀ ∈ S, L₁ ∈ £, and is a strong right representation of L₁. If L₁ can be stabilized by canonical controller , then L₁ − L₀ can be stabilized by some canonical controller.

Proof. Since L₀ ∈ S, then is a strong right representation of L₁ − L₀. By Lemma 10, stabilizes L₁ if and only if D = M₁ − K₂₂M₁ − K₂₁N₁ is invertible in S. Suppose stabilizes L₁ − L₀; then by Lemma 10,

()

is invertible in S. Define R₂₁ = K₂₁ ∈ S, R₂₂ = K₂₂ + K₂₁L₀ ∈ S; thus D^′ is invertible in S, and

stabilizes L₁ − L₀.

The conditions of Corollary 12 are weaker than those of Corollary 11. In following, we will discuss the stabilization of {L, K} with coprime factorizations.

Theorem 13. The canonical controller stabilizes L if and only if Δ = I − K₂₂ − K₂₁L ∈ £ is invertible in S and LΔ⁻¹ ∈ S.

Proof. Let K₁₁ = 0, K₁₂ = I, K₂₁, K₂₂ ∈ S; from Theorem 8, we have that Δ = I − K₂₂ − K₂₁L ∈ £ is invertible in S and LΔ⁻¹ ∈ S.

Remark 14. When K₁₁ = 0, , thus K₁₁ = 0 is an admissible controller for L; we do not need to emphasize this in Theorem 13.

Remark 15. By Remark 14, L ∈ £, but , K₁₁ = 0 is not a stabilizing controller for L, but is a stabilizing controller with internal loop for L.

Theorem 16. If L has right coprime factorization NM⁻¹, then L can be stabilized by canonical controller if and only if M − K₂₂M − K₂₁N is invertible in S.

Proof. By Theorem 13, {L, K} is stable if and only if Δ⁻¹, LΔ⁻¹ ∈ S. Consider L = NM⁻¹; then Δ⁻¹ = M(M − K₂₂M − K₂₁N) ⁻¹, LΔ⁻¹ = N(M − K₂₂M − K₂₁N) ⁻¹. If M − K₂₂M − K₂₁N ∈ S, then Δ⁻¹, LΔ⁻¹ ∈ S. Conversely, if Δ⁻¹, LΔ⁻¹ ∈ S and , then .

Theorem 17. If L has right coprime factorization NM⁻¹ if and only if L can be stabilized by some canonical controller.

Proof. If NM⁻¹ is right coprime factorization of L, there exist Y, X ∈ S such that . Take K₂₁ = −X ∈ S, K₂₂ = I − Y ∈ S; then M − K₂₂M − K₂₁N = YM + XN = I is invertible in S. By Theorem 13, stabilizes L.

Conversely, If stabilizes L, by Theorem 13, Δ⁻¹ ∈ S, LΔ⁻¹ ∈ S. Take M = Δ⁻¹, N = LΔ⁻¹, Y = I − K₂₂ ∈ S, X = −K₂₁ ∈ S; then YM + XN = (I − K₂₂)Δ⁻¹ − K₂₁LΔ⁻¹ = I; thus, NM⁻¹ is right coprime factorization of L.

We expect a strong relationship between stabilization with internal loop and the usual concept of stabilization by the parameterization of all stabilizing (dual) canonical controllers.

Theorem 18. Suppose that L has a doubly coprime factorization; then all canonical controllers that stabilize L with internal loop are parameterized by

()

where Q ∈ S, E ∈ S∩S⁻¹.

Proof. Take , , where E ∈ S∩S⁻¹, Q ∈ S; then ; by Theorem 17, K stabilizes L.

Conversely, if K stabilizes L, by Theorem 16, D = M − K₂₂M − K₂₁N is invertible in S. Consider I = D⁻¹(I − K₂₂)M − D⁻¹K₂₁N; thus is a left inverse of . By Theorem 17, there exist Q ∈ S such that , , rewrite these as , .

The following Theorem contains the dual statements of Theorems 13, 16, 17 and 18.

Theorem 19. (a) The dual canonical controller stabilizes L if and only if is invertible in S and .

(b) If L has left coprime factorization , then L can be stabilized by canonical controller if and only if is invertible in S.

(d) Suppose that L has a doubly coprime factorization, then all dual canonical controllers that stabilize L with internal loop are parameterized by

()

where Q ∈ S, E ∈ S∩S⁻¹.

The Proof of (c). Suppose , there exist such that . Let , , then , L can be stabilized by .

Conversely, if L can be stabilized by , by (1), , . Let , , , , then , , thus is a left coprime factorization of L.

Theorem 20. If the canonical controller stabilizes L, then L can be stabilized by the dual canonical controller .

Proof. If L can be stabilized by the canonical controller , by Theorems 13 and 17, Δ⁻¹ = (I − K₂₂ − K₂₁L) ⁻¹ ∈ S, LΔ⁻¹ ∈ S, and L has a right coprime factorization. From [17], we known that L has a left coprime factorization and there exist such that . Let , . In the following, we need to prove (1) and (2) stabilizes L.

= = = .

Since = + + , so .

− is invertible in S, = . By Theorem 19(a), stabilizes L.

Notice that if a canonical K stabilizes L with internal loop, then K₂₁ and I − K₂₂ are left coprime, since (I − K₂₂Δ⁻¹) − K₂₁LΔ⁻¹ = I. Theorem 20 has a dual statement for right-coprime factorizations K.

There is a similar result for the dual canonical controller.

Theorem 21. If the dual canonical controller stabilizes L, then L can be stabilized by the dual canonical controller .

The proof of Theorem 21 is similar to that of Theorem 20, and we omit it.

5. Conclusion

In this paper, we investigate the dynamic stabilization of a large class of transfer functions in the framework of nest algebra. To obtain a natural generalization of dynamic stabilization, we introduce a new concept of stabilization by a controller with internal loop. The concept enables a simple Youla parameterization and has some advantages which turn out to be very important for infinite-dimensional systems. It makes the theory of dynamic stabilization simpler and more natural.

We also analyze canonical and dual canonical controllers, which are controllers with internal loop of a special (simple) structure. We have found that these are closely related to (doubly) coprime factorization, and we have given a complete parameterization of all stabilizing controllers with internal loop which are (dual) canonical.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

References

1 De la Sen M., Stability of switched feedback time-varying dynamic system based on the properties of the gap metric for operators, Abstract and Applied Analysis. (2012) 2012, 17, 612198, https://doi.org/10.1155/2012/612198.
10.1155/2012/612198
Google Scholar
2 De La Sen M., On the characterization of hankel and toeplitz operators describing switched linear dynamic systems with point delays, Abstract and Applied Analysis. (2009) 2009, 34, 2-s2.0-69449101809, https://doi.org/10.1155/2009/670314, 670314, ZBL1200.37019.
10.1155/2009/670314
Google Scholar
3 Feintuch A., Robust Control Theory in Hilbert Space, 1998, Springer, New York, NY, USA.
10.1007/978-1-4612-0591-3
Google Scholar
4 Dullerud G. E. and Paganini F., A Course in Robust Control Theory, 2000, Springer.
10.1007/978-1-4757-3290-0
Web of Science® Google Scholar
5 Pastravanu O. and Matcovschi M.-H., Stability of matrix polytopes with a dominant vertex and implications for system dynamics, Abstract and Applied Analysis. (2013) 2013, 11, 396759, https://doi.org/10.1155/2013/396759.
10.1155/2013/396759
Google Scholar
6 Li S.-Y., Yang C.-H., Ko L.-W. et al., Implementation on electronic circuits and RTR pragmatical adaptive synchronization: time-reversed uncertain dynamical systems′ analysis and applications, Abstract and Applied Analysis. (2013) 2013, 10, 909721, https://doi.org/10.1155/2013/909721, ZBL06209492.
10.1155/2013/909721
Google Scholar
7 Curtain R. F., Weiss G., and Weiss M., A. A. Borichev and N. K. Nikolski, Stabilization of irrational transfer functions by controllers with in- ternal loop, System, approximation, singular integral operators and related topics, International Workshop on Operator Theory and Applications, IWOTA, Advances in Operator Theory and Applications, 2000, Birkhäuser, Basel, Switzerland, 179–207.
Google Scholar
8 Weiss G. and Curtain R. F., Dynamic stabilization of regular linear systems, IEEE Transactions on Automatic Control. (1997) 42, no. 1, 4–21, 2-s2.0-0030785154, https://doi.org/10.1109/9.553684, ZBL0876.93074.
10.1109/9.553684
Web of Science® Google Scholar
9 Ma L., Wang Z., Bo Y., and Guo Z., A game theory approach to mixed H₂/H_∞ control for a class of stochastic time-varying systems with randomly occurring nonlinearities, Systems and Control Letters. (2011) 60, no. 12, 1009–1015, 2-s2.0-80054077895, https://doi.org/10.1016/j.sysconle.2011.08.009.
10.1016/j.sysconle.2011.08.009
Web of Science® Google Scholar
10 Hu J., Wang Z., Gao H., and Stergioulas L. K., Probability-guaranteed H_∞ finite-horizon filtering for a class of nonlinear time-varying systems with sensor saturations, Systems and Control Letters. (2012) 61, no. 4, 477–484, 2-s2.0-84859559079, https://doi.org/10.1016/j.sysconle.2012.01.005.
10.1016/j.sysconle.2012.01.005
Web of Science® Google Scholar
11 Wei G., Wang Z., and Shen B., Error-constrained finite-horizon tracking control with incomplete measurements and bounded noises, International Journal of Robust and Nonlinear Control. (2012) 22, no. 2, 223–238, 2-s2.0-84855320493, https://doi.org/10.1002/rnc.1728, ZBL1244.93083.
10.1002/rnc.1728
Web of Science® Google Scholar
12 Shen B., Wang Z., Shu H., and Wei G., H_∞ filtering for uncertain time-varying systems with multiple randomly occurred nonlinearities and successive packet dropouts, International Journal of Robust and Nonlinear Control. (2011) 21, no. 14, 1693–1709, 2-s2.0-80051638477, https://doi.org/10.1002/rnc.1662.
10.1002/rnc.1662
Web of Science® Google Scholar
13 Chen Y., Bi W., and Li W., New delay-dependent absolute stability criteria for Lur′e systems with time-varying delay, International Journal of Systems Science. (2011) 42, no. 7, 1105–1113, 2-s2.0-79959551140, https://doi.org/10.1080/00207720903308348, ZBL1235.34193.
10.1080/00207720903308348
Web of Science® Google Scholar
14 de la Sen M. and Ibeas A., On the global asymptotic stability of switched linear time-varying systems with constant point delays, Discrete Dynamics in Nature and Society. (2008) 2008, 31, 2-s2.0-60549106700, https://doi.org/10.1155/2008/231710, 231710.
10.1155/2008/231710
Web of Science® Google Scholar
15 Lu Y. and Shi C., Stabilization of time-varying system by controller with internal loop, Mathematical Problems in Engineering. (2012) 2012, 16, 132597, https://doi.org/10.1155/2012/132597.
10.1155/2012/132597
Web of Science® Google Scholar
16 Baras J. S., Frequency domain design of linear distributed system, Proceedings of the 19th IEEE Decision and Control Conference, December 1980, 728–732, 2-s2.0-0019240916.
Google Scholar
17 Curtain R., Weiss G., and Weiss M., Coprime factorization for regular linear systems, Automatica. (1996) 32, no. 11, 1519–1531, 2-s2.0-0030284751, https://doi.org/10.1016/S0005-1098(96)00102-1.
10.1016/S0005-1098(96)00102-1
Web of Science® Google Scholar
18 Townley S., Weiss G., and Yamamoto Y., Diseretizing continuous-time controllers for infinite-dimensional linear systems, Proceedings of the MTNS Symposium, July 1998, Padova, Italy, 547–550.
Google Scholar

Citing Literature

All articles

Stabilization with Internal Loop for Infinite-Dimensional Discrete Time-Varying Systems

Abstract

1. Introduction

2. Preliminaries

3. Stabilization with Internal Loop

4. Canonical and Dual Canonical Controllers

5. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Stabilization with Internal Loop for Infinite-Dimensional Discrete Time-Varying Systems

Abstract

1. Introduction

2. Preliminaries

3. Stabilization with Internal Loop

4. Canonical and Dual Canonical Controllers

5. Conclusion

Conflict of Interests

References

Citing Literature

Figures

References

Related

Information