We present a probabilistic analysis on conditions of the exact recovery of block-sparse signals whose nonzero elements appear in fixed blocks. We mainly derive a simple lower bound on the necessary number of Gaussian measurements for exact recovery of such block-sparse signals via the mixed l₂/l_q (0 < q ≤ 1) norm minimization method. In addition, we present numerical examples to partially support the correctness of the theoretical results. The obtained results extend those known for the standard l_q minimization and the mixed l₂/l₁ minimization methods to the mixed l₂/l_q (0 < q ≤ 1) minimization method in the context of block-sparse signal recovery.

1. Introduction and Main Results

The problem of block-sparse signal recovery naturally arises in a number of genetics, image processing, and machine learning tasks. Prominent examples include DNA microarrays [1], wavelet sparsity modeling [2], color imaging [3], and wideband spectrum sensing [4]. In these contexts, we often require to recover an unknown signal

from an underdetermined system of linear equations y = Φx, where

are available measurements and Φ is a M × N (M < N) measurement matrix. Unlike previous works in compressed sensing (CS) [5–7], the unknown signal x not only is sparse but also exhibits additional structure in the form where the nonzero coefficients appear in some fixed blocks. We refer to such a structured sparse vector as block-sparse signal in this paper. Following [8–11], we only consider the nonoverlapping case in the present study. Thus, from mathematical point, a block signal

can be viewed as concatenation of x in m blocks of length d; that is,

(1)

where x[i] denotes the ith block of x and N = md (m, d ∈ Z⁺). In these terms, we say that x is block k-sparse if x[i] has nonzero Euclidean norm for at most k blocks. In this paper, we furthermore assume that each element in these k nonzero blocks has nonzero coefficient. Obviously, if d = 1, the block-sparse signal degenerates to the conventional sparse signal well studied in compressed sensing.

Denote

(2)

where I(∥x[i]∥₂ > 0) is an indicator function; that is, I(‖x[i]‖₂ > 0) = 1, if ‖x[i]‖₂ > 0; I(‖x[i]‖₂ > 0) = 0, otherwise. Thus a block k-sparse signal x can be defined as a signal that satisfies ‖x‖_2,0 ≤ k. It is known that, under certain conditions on measurement matrix Φ (i.e., [8]), there is a unique block-sparse signal that obeys the observation y = Φx and can be exactly recovered by solving the problem

(3)

Similar to the standard l₀ minimization problem, (3) is NP-hard and computationally intractable except for very small size. Motivated by the study of CS, one then commonly uses the strategy to replace the l₂/l₀ norm with its closest convex surrogate l₂/l₁ norm, thus to solve a mixed l₂/l₁ norm minimization problem:

(4)

where

. This model can be treated as a second-order cone program (SOCP) problem and many standard software packages can be used for the solutions very efficiently. In many practical cases, the measurements y are corrupted by bounded noise; then we can apply the modified SOCP or the group version of basis pursuit denoising (BPDN, [12]) program as the following:

(5)

where λ is a tuning parameter, which controls the tolerance of the noise term. There are also many methods to solve this optimization problem efficiently, such as the block-coordinate descent technique [13] and the Landweber iterations technique [14]. Conditions under which solving problem (4) can successfully recover a block-sparse signal x have been extensively studied [8, 10, 15]. For example, Eldar and Mishali [8] generalized the conventional RIP notion to the block-sparse setting and showed that if Φ satisfies the block-RIP (see Definition 1) with constant δ_2k < 0.414, solving (4) can accurately get any block-sparse solution of y = Φx.

Among the latest researches in compressed sensing, many authors [16–21] have showed that l_q minimization with 0 < q < 1 allows the exact recovery of conventional sparse signals from much fewer linear measurements than that by l₁ minimization. Naturally, it would be interesting to make an ongoing effort to extend l_q (0 < q < 1) minimization to the setting of block-sparsity. Specifically, the following mixed l₂/l_q (0 < q ≤ 1) norm minimization problem is proposed (see [11])

(6)

for block-sparse signal recovery, as a generalization of the standard l_q minimization, where . Similar to the standard l_q minimization problem, (6) is also a nonconvex problem for any 0 < q < 1, and finding its global minimizer is in general computationally impossible. However, it is well known that there are several efficient heuristic methods to compute local minimizers of the standard l_q (0 < q ≤ 1) minimization problem; say, for example, [18, 22]. One can generalize those approaches to solve the mixed l₂/l_q minimization problem (6). In particular, we will adopt the iteratively reweighted least squares techniques in this paper.

In [17], Chartrand and Staneva conducted a detailed analysis of the l_q (0 < q ≤ 1) minimization approach for the nonblock sparse recovery problem. They derived a lower bound of Gaussian measurement for exact recovery of a nonblock sparse signal. Furthermore, Eldar and Mishali [8] also provided a lower bound on block-sparse signal recovery in the Gaussian measurement ensemble for the mixed l₂/l₁ minimization. Along this line, we will provide in this paper a lower bound of Gaussian measurements for exact recovery of block-sparse signal through the mixed l₂/l_q (0 < q ≤ 1) norm minimization. The obtained results will complement the results of [8, 17] and demonstrate particularly that the block version of l_q (0 < q ≤ 1) minimization can reduce the number of Gaussian measurements necessary for the exact recovery as q decreases.

To introduce our results, we first state the definition of block-RIP [8] as follows.

Definition 1 (see [8].)Let be an M × N measurement matrix. One says that Φ has the block-RIP over (then N = md) with constant if for every block k-sparse signal over such that

(7)

This new definition of block-RIP is crucial for our analysis of the mixed l₂/l_q (0 < q ≤ 1) minimization method. For convenience, we still use δ_k instead of , henceforth to represent the block-RIP constant of order k. With this notion, we can prove the following sufficient condition for exact recovery of a block k-sparse signal.

Theorem 2. Let be an arbitrary block k-sparse signal. For any given q ∈ (0,1], if the measurement matrix has the block-RIP (7) with constant

(8)

then the mixed l₂/l_q minimization problem (6) has a unique solution, given by the original signal x.

Condition (8) generalizes the condition of the mixed l₂/l₁ case in [8] to the mixed l₂/l_q (0 < q ≤ 1) case. Note that the right-hand side of (8) is monotonically decreasing with q, which shows that decreasing q can get weaker recovery condition. This shows further that fewer measurements might be needed to recover a block k-sparse signal whenever the mixed l₂/l_q (0 < q < 1) minimization methods are used instead of the mixed l₂/l₁ minimization method. For clarifying this issue more precisely, we can adopt a similar probabilistic method of [17] to derive a simple lower bound on how many random Gaussian measurements are sufficient for (8) to hold with high probability. The result to be verified is in Section 3.

Theorem 3. Let Φ be a M × N matrix with i.i.d. zero-mean unit variance Gaussian entries and N = md for some integer m. For any given q ∈ (0,1], if

(9)

then the subsequent conclusion is true with probability exceeding : Φ satisfies (8); therefore, any block k-sparse signal can be recovered exactly by the solution of the mixed l₂/l_q minimization problem (6).

Theorem 3 shows that a block k-sparse signal x can be recovered exactly with high probability by solving the mixed l₂/l_q minimization (6) provided the number of Gaussian measurements M satisfies

(10)

More detailed remarks on this bound will be presented in Section 3.

The rest of the paper is organized as follows. In Section 2, we present several key lemmas needed for the proofs of our main results. All these lemmas can be regarded as generalizations of the standard non-block-sparse case to the block-sparse case. The proofs of Theorems 2 and 3 are given in Section 3. Numerical experiments are provided in Section 4 to demonstrate the correctness of the theoretical results. We conclude the paper then in Section 5 with some useful remarks.

2. Fundamental Lemmas

In this section, we establish several lemmas necessary for the proofs of the main results.

Lemma 4 (see [8].)Consider

(11)

for all x, x^′ supported on disjoint subsets T, T^′⊆{1,2, …, N} with |T | < k, |T^′ | < k^′.

In the next lemma, we show that the probability that block restricted isometry constant δ_k exceeds a certain scope decays exponentially in certain length of x.

Lemma 5 (see [8].)Suppose Φ is an M × N matrix from the Gaussian ensemble; namely, Φ_ij ~ N(0, 1/M). Let be the smallest value satisfying the block-RIP of Φ over I = {d₁ = d, d₂ = d, …, d_m = d} and N = md for some integer m. Then, for every ϵ > 0, the block restricted isometry constant satisfies the following inequality:

(12)

which holds with high probability 2e^{−mH(kd/N)ϵ}, where H(p) = −plog⁡(p)−(1 − p)log⁡(1 − p) (0 < p < 1).

Lemma 6. Suppose Φ is an M × N matrix from the Gaussian ensemble; namely, Φ_ij ~ N(0, 1/M). For any 0 < δ < 1, the following estimation

(13)

holds uniformly for with probability exceeding 1 − 2(12/δ) ^Le^{−M(1 + δ/2)mH(k/m)/k}.

Proof. Note that [23] has verified the subsequent conclusion: if Φ is a random matrix of size M × N drawn according to a distribution that satisfies the concentration inequality , where c₀(β) is a constant dependent only on β such that c₀(β) > 0 for 0 < β < 1, then, for any set T with |T | = k < n and any 0 < δ < 1, there holds the estimation

(14)

with probability exceeding . By Lemma 5, the concentration inequality is clearly true for Gaussian measurement matrix. Thus Lemma 6 follows.

We also need the following inequality.

Lemma 7 (see [24].)For any fixed q ∈ (0,1) and ,

(15)

3. Proofs of Theorems

With the preparations made in the last section, we now prove the main results of the paper. Henceforth, we let Φ denote an M × N matrix whose elements are i.i.d. random variables; specifically, Φ_ij ~ N(0, 1/M). We prove Theorem 2 by using the block-RIP and Lemmas 4 and 7.

Proof of Theorem 2. First notice that assumption (8) implies δ_2k < 1 and further implies the uniqueness of x satisfying the observation y = Φx. Let x^* = x + h be a solution of (6). Our goal is then to show that h = 0. For this purpose, we let x_T be the signal that is identical to x on the index set T and to zero elsewhere. Let T₀ be the block index set over the k nonzero blocks of x, and we decompose h into a series of vectors such that

(16)

Here is the restriction of h onto the set T_i and each T_i consists of k blocks (except possibly T_J). Rearrange the block indices such that , for any j ≥ 1.

From [9], x^* is the unique sparse solution of (6) being equal to x if and only if

(17)

for all nonzero signal h in the null space of Φ. This is the so-called the null space property (NSP). In order to characterize the NSP more precisely, we consider the following equivalent form: there exists a constant γ(h, q) satisfying 0 < γ(h, q) < 1 such that

(18)

We proceed by showing that γ(h, q) < 1 under the assumption of Theorem 2.

In effect, we observe that

(19)

For any j ≥ 2, if we denote , , , then we have

(20)

By Lemma 7, we thus have

(21)

that is,

(22)

On the other hand, let

(23)

It is easy to see that

(24)

Since Φx = Φx^*, we have Φh = 0, which means . By the definition of block-RIP, Lemma 4, (22), and (24), it then follows that

(25)

By the definition of block-RIP δ_2k and by using Hölder’s equality, we then get

(26)

This together with (24) and (25) implies

(27)

Through a straightforward calculation, one can check that the maximum of f(t) occurs at t₀ = (1 − q/2)/(2 − δ_2k) and

(28)

If f(t₀) < 1, then we clearly have γ(h, q) < 1 and finish the proof. However, f(t₀) < 1 gives that

(29)

or, equivalently,

(30)

Note that (30) implies 0 < δ_2k < 1/2 and

(31)

By simple calculations, we can check that, for any given q ∈ (0,1], inequality (30) is true as long as

(32)

that is, condition (8) is satisfied. With this, the proof of Theorem 2 is completed.

Now we adopt the probabilistic methods to analyze how condition (8) can be satisfied; particularly, how many measurements are needed for exact recovery of a block k-sparse signal.

Proof of Theorem 3. From Theorem 2, we only need to show that, under condition (9), (8) holds with high probability. In particular, we will proceed to determine how random Gaussian measurements are sufficient for exact recovery of block k-sparse signals with a failure probability at most . To this end, we let L = 2kd. Then by Lemma 6, an upper bound for the probability that any M × L submatrix of Φ fails to satisfy the block-RIP (30) is

(33)

By inequality , it suffices to show that we can have the following estimation:

(34)

So by a simple calculation,

(35)

where C₁(q) = (3 − log⁡2 + dlog⁡(12/(1/2 − (q/4)(2/3 − q/3) ^2/q−1)))/(1 + 1/4 − (q/8)(2/3 − q/3)^2/q−1)(m/k)H(k/m), C₂(q) = 3/(1 + 1/4 − (q/8)(2/3 − q/3)^2/q−1)(m/k)H(k/m). That is, (35) is satisfied as long as (9) is met. This justifies Theorem 3.

Remark 8. From the right-hand side of (35), we can further see that, except the first term related to m/k, other terms in the numerator are only related to k and d, that is, to the numbers of nonzero blocks and the block size. Obviously, those terms have a smaller contribution to the number of measurements. Basically, Theorem 3 shows that the signal x with block-sparsity ‖x‖_2,0 ≤ k can be recovered exactly by the solution of the mixed l₂/l_q minimization (6) with high probability provided roughly

(36)

Obviously, this result generalizes the well-known result in [8] on the Gaussian ensemble for the mixed l₂/l₁ minimization. We can further see from Theorem 3 that, when specified to q = 1, the bound (36) has the same order as Eldar’s result (O(klog⁡(m/k)), see [8]). It is also obvious that C(q) is monotonically increasing with respect to q ∈ (0,1], which then implies that decreasing q allows fewer necessary measurements for exact recovery of block-sparse signals by the mixed l₂/l_q minimization method. Since, when block size d = 1, the mixed l₂/l_q minimization method degenerates to the standard l_q minimization method, the presented result then provides a theoretical support to such experimental observation reported in the following section.

4. Numerical Experiments

In this section, we conduct two numerical experiments to support the correctness of the obtained theoretical results. Iteratively reweighted least squares (IRLS) method has been proved to be very efficient for the standard l_q minimization. Thus, in the experiments, we adopted IRLS method to solve the following unconstrained smoothed version of (6):

(37)

where τ is a regularization parameter and

. Note that, through defining a diagonal weighting matrix W as

, (37) can be transformed to the following weighted least squares minimization problem:

(38)

With this, the IRLS algorithm we used can be summarized as follows (more details can be found in [11]).

Step 1. Set the iteration count t to zero and ϵ₀ = 1. Initialize .

Step 2. Let

(39)

and update

(40)

Step 3. Terminate the iteration on convergence or when t attains a specified maximum number t_max⁡.

Otherwise, set t = t + 1 and go to Step 2.

The above algorithm can be seen as a natural generalization of general sparse signal recovery algorithm to the block-sparse setting, which alternates between estimating x and redefining the weighting matrix W. Though this algorithm is for the unconstrained penalized problem (37), it can still give a good estimation on the minimum of the constrained problem (6) when we choose a sufficient small τ (such as τ = 10⁻⁶). In the following experiments, we set τ = 10⁻⁶ and terminate the algorithm if ϵ < 10⁻⁷ or .

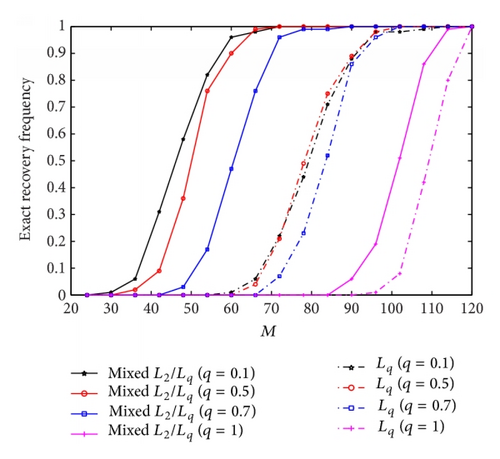
In our first experiment, we took the signal length N = 128, the block size d = 4, and the block-sparsity k = 6. For independent 100 trails, we first randomly generated the block-sparse signal x with values from a Gaussian distribution of mean 0 and standard deviation 1, and then we randomly drew a measurement matrix Φ from Gaussian ensemble. We also took the number of measurements varying from 24 to 124. The purpose of the experiment was then to check the correctness of Theorem 3. We considered four different values of q = 0.1,0.5,0.7,1 for both the mixed l₂/l_q minimization method and the standard l_q minimization method.

The experiment result is shown in Figure 1. It is seen from Figure 1 that, for all the experiment runs, the smaller q requires the smaller number of measurements for exact recovery of block sparse signals. This observation is consistent with Theorem 3. On the other hand, for a fixed q, the mixed l₂/l_q method is clearly superior to the standard l_q method in this block-sparse setting. For instance, the mixed l₂/l_q method with q = 0.1 only uses 50 Gaussian measurements for the exact recovery, while the number of measurements needed for l_q method is around 90. This observation also partially supports the theoretical assertion of Theorem 3, namely, that incorporating the block structure into recovery method requires fewer measurements for exact recovery.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Plots of the exact recovery frequency versus the number of measurements, for the use of the mixed l₂/l_q and the standard l_q minimization methods with different values of q.

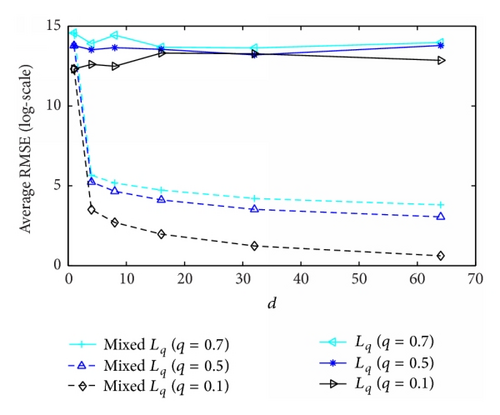
In our second experiment, we further studied the effect of block size d for block-sparse signal recovery. We set N = 256 and drew a measurement matrix of size 128 × 256 from Gaussian ensemble. In this experiment, the block size d was changed while keeping the total sparsity kd = 64 fixed. Figure 2 shows the average root mean squares error (RMSE). Here RMSR is defined as in the logarithmic scale over 100 independent random runs. One can easily see from Figure 2 that the recovery performance for the standard l_q method is independent of the active block number k, while the recovery errors for the mixed l₂/l_q method are significantly better than the standard l_q method when the active block number k is far smaller than the total signal sparsity kd. Since the total sparsity kd is fixed and larger d leads to smaller k, as predicted by Theorem 3, the necessary measurement number needed for exact recovery of a block k-sparse signal by the mixed method is also reduced. This also demonstrates the advantage of the mixed l₂/l_q method over the standard l_q method.

5. Conclusion

In this paper, the number of Gaussian measurements necessary for the exact recovery of a block-sparse signal by the mixed l₂/l_q (0 < q ≤ 1) norm minimization has been studied. The main contribution is the derivation of a lower bound on the necessary number of Gaussian measurements for the exact recovery based on a probabilistic analysis with block-RIP. The obtained results are helpful for understanding the recovery capability and algorithm development of the mixed l₂/l_q norm minimization approach for sparse recovery and, particularly, facilitate the applications in the development of block-sparse information processing.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This work has been supported by the Natural Science Foundation of China under Grant nos. 61303168, 61273020, and 11171272.

References

1 Parvaresh F., Vikalo H., Misra S., and Hassibi B., Recovering sparse signals using sparse measurement matrices in compressed DNA microarrays, IEEE Journal on Selected Topics in Signal Processing. (2008) 2, no. 3, 275–285, https://doi.org/10.1109/JSTSP.2008.924384, 2-s2.0-47049098617.
10.1109/JSTSP.2008.924384
Web of Science® Google Scholar
2 Rao N. S., Nowak R. D., Wright S. J., and Kingsbury N. G., Convex approaches to model wavelet sparsity patterns, Proceedings of the 18th IEEE International Conference on Image Processing (ICIP ′11), September 2011, 1917–1920, https://doi.org/10.1109/ICIP.2011.6115845, 2-s2.0-84856264699.
10.1109/ICIP.2011.6115845
Google Scholar
3 Majumdar A. and Ward R. K., Compressed sensing of color images, Signal Processing. (2010) 90, no. 12, 3122–3127, https://doi.org/10.1016/j.sigpro.2010.05.016, ZBL1197.94089, 2-s2.0-77955414367.
10.1016/j.sigpro.2010.05.016
Web of Science® Google Scholar
4 Mishali M. and Eldar Y. C., Blind multiband signal reconstruction: compressed sensing for analog signals, IEEE Transactions on Signal Processing. (2009) 57, no. 3, 993–1009, https://doi.org/10.1109/TSP.2009.2012791, MR3027782, 2-s2.0-61549103040.
10.1109/TSP.2009.2012791
Web of Science® Google Scholar
5 Donoho D. L., Compressed sensing, IEEE Transactions on Information Theory. (2006) 52, no. 4, 1289–1306, https://doi.org/10.1109/TIT.2006.871582, MR2241189, 2-s2.0-33645712892.
10.1109/TIT.2006.871582
Web of Science® Google Scholar
6 Candès E. J., Romberg J., and Tao T., Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information, IEEE Transactions on Information Theory. (2006) 52, no. 2, 489–509, https://doi.org/10.1109/TIT.2005.862083, MR2236170, 2-s2.0-31744440684.
10.1109/TIT.2005.862083
Web of Science® Google Scholar
7 Candes E. J. and Tao T., Near-optimal signal recovery from random projections: universal encoding strategies?, IEEE Transactions on Information Theory. (2006) 52, no. 12, 5406–5425, https://doi.org/10.1109/TIT.2006.885507, MR2300700, 2-s2.0-33947416035.
10.1109/TIT.2006.885507
Web of Science® Google Scholar
8 Eldar Y. C. and Mishali M., Robust recovery of signals from a structured union of subspaces, IEEE Transactions on Information Theory. (2009) 55, no. 11, 5302–5316, https://doi.org/10.1109/TIT.2009.2030471, MR2596977, 2-s2.0-70350743173.
10.1109/TIT.2009.2030471
Web of Science® Google Scholar
9 Stojnic M., Parvaresh F., and Hassibi B., On the reconstruction of block-sparse signals with an optimal number of measurements, IEEE Transactions on Signal Processing. (2009) 57, no. 8, 3075–3085, https://doi.org/10.1109/TSP.2009.2020754, MR2723043, 2-s2.0-68249141421.
10.1109/TSP.2009.2020754
Web of Science® Google Scholar
10 Eldar Y. C., Kuppinger P., and Bolcskei H., Block-sparse signals: uncertainty relations and efficient recovery, IEEE Transactions on Signal Processing. (2010) 58, no. 6, 3042–3054, https://doi.org/10.1109/TSP.2010.2044837, MR2730246, 2-s2.0-77952576986.
10.1109/TSP.2010.2044837
Web of Science® Google Scholar
11 Wang Y., Wang J., and Xu Z., On recovery of block-sparse signals via mixed l₂ = lq(0 < q ≤ 1) norm minimization, Eurasip Journal on Advances in Signal Processing. (2013) 2013, no. 1, article 76, https://doi.org/10.1186/1687-6180-2013-76, 2-s2.0-84886711132.
10.1186/1687-6180-2013-76
Google Scholar
12 Chen S. S., Donoho D. L., and Saunders M. A., Atomic decomposition by basis pursuit, SIAM Journal on Scientific Computing. (1998) 20, no. 1, 33–61, https://doi.org/10.1137/S1064827596304010, MR1639094, 2-s2.0-0032131292.
10.1137/S1064827596304010
CAS Web of Science® Google Scholar
13 Yuan M. and Lin Y., Model selection and estimation in regression with grouped variables, Journal of the Royal Statistical Society B. (2006) 68, no. 1, 49–67, https://doi.org/10.1111/j.1467-9868.2005.00532.x, MR2212574, 2-s2.0-33645035051.
10.1111/j.1467-9868.2005.00532.x
Web of Science® Google Scholar
14 Fornasier M. and Rauhut H., Recovery algorithms for vector-valued data with joint sparsity constraints, SIAM Journal on Numerical Analysis. (2008) 46, no. 2, 577–613, https://doi.org/10.1137/0606668909, MR2383204, 2-s2.0-36749019495.
10.1137/0606668909
Web of Science® Google Scholar
15 Huang J. and Zhang T., The benefit of group sparsity, The Annals of Statistics. (2010) 38, no. 4, 1978–2004, https://doi.org/10.1214/09-AOS778, MR2676881, 2-s2.0-77955136689.
10.1214/09-AOS778
Web of Science® Google Scholar
16 Chartrand R., Exact reconstruction of sparse signals via nonconvex minimization, IEEE Signal Processing Letters. (2007) 14, no. 10, 707–710, https://doi.org/10.1109/LSP.2007.898300, 2-s2.0-34548724437.
10.1109/LSP.2007.898300
Web of Science® Google Scholar
17 Chartrand R. and Staneva V., Restricted isometry properties and nonconvex compressive sensing, Inverse Problems. (2008) 24, no. 3, 14, 035020, https://doi.org/10.1088/0266-5611/24/3/035020, MR2421974, 2-s2.0-44449127493.
10.1088/0266-5611/24/3/035020
Web of Science® Google Scholar
18 Foucart S. and Lai M. J., Sparsest solutions of underdetermined linear systems via l_q-minimization for 0 < q ≤ 1, Applied and Computational Harmonic Analysis. (2009) 26, no. 3, 395–407.
10.1016/j.acha.2008.09.001
Web of Science® Google Scholar
19 Xu Z., Zhang H., Wang Y., Chang X., and Liang Y., L_1/2 regularization, Science China. Information Sciences. (2010) 53, no. 6, 1159–1169, https://doi.org/10.1007/s11432-010-0090-0, MR2671451, 2-s2.0-84860280270.
10.1007/s11432-010-0090-0
Web of Science® Google Scholar
20 Xu Z., Chang X., Xu F., and Zhang H., L_1/2 regularization: a thresholding representation theory and a fast solver, IEEE Transactions on Neural Networks and Learning Systems. (2012) 23, no. 7, 1013–1027, https://doi.org/10.1109/TNNLS.2012.2197412, 2-s2.0-84871085657.
10.1109/TNNLS.2012.2197412
PubMed Web of Science® Google Scholar
21 Sun Q., Recovery of sparsest signals via ℓq-minimization, Applied and Computational Harmonic Analysis. (2012) 32, no. 3, 329–341, https://doi.org/10.1016/j.acha.2011.07.001, MR2892737, 2-s2.0-84857781336.
10.1016/j.acha.2011.07.001
Web of Science® Google Scholar
22 Daubechies I., DeVore R., Fornasier M., and Güntürk C. S., Iteratively reweighted least squares minimization for sparse recovery, Communications on Pure and Applied Mathematics. (2010) 63, no. 1, 1–38, https://doi.org/10.1002/cpa.20303, MR2588385, 2-s2.0-77949704355.
10.1002/cpa.20303
Web of Science® Google Scholar
23 Baraniuk R., Davenport M., DeVore R., and Wakin M., A simple proof of the restricted isometry property for random matrices, Constructive Approximation. (2008) 28, no. 3, 253–263, https://doi.org/10.1007/s00365-007-9003-x, MR2453366, 2-s2.0-55649115527.
10.1007/s00365-007-9003-x
Web of Science® Google Scholar
24 Lai M. J. and Liu L. Y., A new estimate of restricted isometry constants for sparse solutions, Applied and Computational Harmonic Analysis. (2011) 30, 402–406, https://doi.org/10.1016/j.acha.2010.11.002.
10.1016/j.acha.2010.11.002
Google Scholar

Citing Literature

All articles

A Simple Gaussian Measurement Bound for Exact Recovery of Block-Sparse Signals

Abstract

1. Introduction and Main Results

2. Fundamental Lemmas

3. Proofs of Theorems

4. Numerical Experiments

5. Conclusion

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Simple Gaussian Measurement Bound for Exact Recovery of Block-Sparse Signals

Abstract

1. Introduction and Main Results

2. Fundamental Lemmas

3. Proofs of Theorems

4. Numerical Experiments

5. Conclusion

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Related

Information