The sensitivity of the main characteristics of baroclinically unstable waves with respect to fundamental parameters of the atmosphere (the static stability parameter σ₀ and vertical shear of a zonal wind Λ) is theoretically explored. Two types of waves are considered: synoptic scale waves and planetary scale (ultralong) waves based on an Eady-type model and model with vertically averaged primitive equations. Sensitivity functions are obtained that estimate the impact of variations in σ₀ and Λ on the growth rate and other characteristics of unstable waves and demonstrate that waves belonging to the short-wave part of the spectrum of unstable waves are more sensitive to changes in the static stability parameter than waves belonging to the long-wave part of the spectrum. The obtained theoretical results show that the increase of the static stability and decrease of the meridional temperature gradient in midlatitude baroclinic zones in some areas of the southern hemisphere lead to a slowing of the growth rate of baroclinic unstable waves and an increasing wavelength of baroclinic unstable wave maximum growth rate, that is, a spectrum shift of unstable waves towards longer wavelengths. These might affect the favorable conditions for the development of baroclinic instability and, therefore, the intensity of cyclone generation activity.

1. Introduction

Static stability and the meridional temperature gradient (MTG) are among the most important fundamental parameters characterizing the state of the atmosphere and, in particular, midlatitude large-scale eddy dynamics [1, 2]. Static stability and MTG play a significant role in the development of baroclinic instability which is the dominant mechanism for generating large-scale atmospheric eddies (cyclones) that form the storm tracks in midlatitudes. The physical nature of baroclinic instability is well understood and explained in the scientific literature, including text books on dynamic meteorology (e.g., [1–4]). Baroclinic instability can be viewed as sloping convection where growing perturbations draw upon the available potential energy which is proportional to a meridional temperature gradient. Since the publication of the pioneering theoretical works of Charney [5] and Eady [6], in which the fundamental baroclinic mechanism of the atmospheric large-scale instability was first described, many scientific papers have been published that examine the growth of initially infinitesimal perturbations in the atmosphere and ocean caused by baroclinic effects. Both linear theory for the onset of baroclinic instability and its nonlinear saturation have been explored in many research articles. A thorough review of baroclinic instability is presented in [7] and to some extent in [8, 9]. Theoretical models of baroclinic instability typically represent linearized dynamics equations and the instability problem is examined as an eigenvalue problem. The nonmodal instability analysis in both linear and nonlinear formulations is more general than eigenanalysis. This technique suggests the solution of a Cauchy (initial value) problem (e.g., [10–12]). Analytical weakly nonlinear theories of baroclinic instability represent a further extension of research (e.g., [13–16]) which focuses on the finite-amplitude behaviour of unstable baroclinic waves. Other areas of studies have explored the life-cycle behaviour of baroclinic unstable waves to understand how initially infinitesimal perturbations grow to large but finite amplitude modifying the mean flow. This kind of research requires numerical integration of the atmospheric nonlinear model equations (e.g., [17–20]).

It is important to underline the significant role of the two-layer model of Philips [21, 22] and its modifications (e.g., [13, 23–28]) in developing baroclinic instability theories. However, for this purpose a two-layer model was usually used in the quasigeostrophic approximation. A generalized baroclinic instability analysis based on two-level primitive-equation model has been described in [29] and applied to detailed consideration of the baroclinic instability mechanism.

There is evidence of an increase over the past decades of the static stability in the extratropics [30] and a pole-ward movement of the midlatitude precipitation zones and storm tracks which are uniquely linked to zones with strong MTG-baroclinic zones (e.g., [31–35]). Recent studies have also indicated an increase in intensity of extratropical cyclones and a decrease in frequency [36–44]. Changes in geographical locations and intensity of storm tracks are more distinct in the southern hemisphere (SH) (e.g., [45]) affecting the essential features of weather patterns over large territories such as Australia [46–54] and indicating a change of favourable conditions for baroclinic instability because the key role of baroclinic instability in the development of midlatitude cyclones is well established.

To study how baroclinic instability has changed in the SH in recent decades, a comparative analysis of climates for periods 1949–1968 and 1975–1994 has been carried out in [50, 54] using National Centres for Environmental Prediction (NCEP) reanalyses and the European Centre for Medium-Range Weather Forecasting (ECMWF) Reanalysis (ERA40) data. As a measure of the baroclinic instability the Phillips criterion [55] adapted to spherical geometry was chosen:

(1)

where

and

are the zonal wind velocities at 300 hPa and 700 hPa isobaric levels, respectively,

is the static stability measure for a given reference state, c_p is the specific heat of air at constant pressure, Ω is the angular rotation speed of the earth, a₀ is the earth’s radius, b_k is a dimensionless constant, and φ is a latitude. J. S. Frederiksen and C. S. Frederiksen [50] obtained a significant decreasing trend in baroclinic instability over the middle latitudes of the SH. The most significant negative trend is localized between 30S and 40S. For instance, the difference between the two periods, 1949–1968 and 1975–1994, reached a maximum of 17% in the SH subtropical jet stream (for the July climate). In addition it was found that further poleward the baroclinic instability intensified creating favourable conditions for cyclogenesis. Using a two-level linearized primitive equation model, Frederiksen et al. [51] studied the growth rate of unstable modes for the July reference state averaged over the above mentioned periods. They identified a 30% reduction in the growth rate of cyclone-scale modes between the two periods.

It should be pointed out that, since the beginning of the 1980s, exploration of the essential features of the atmospheric general circulation in the SH has been facilitated by the availability of plentiful satellite upper-air data. In particular, the importance of baroclinic instability and large-scale eddies in the formation of zonal wind characteristics, such as a tropospheric double-jet phenomenon, was studied in [56, 57].

Taking into account the significant role of baroclinic instability in the development of midlatitude cyclones and the intensity changes of baroclinic instability in some areas of the SH in recent decades, this paper examines the sensitivity of the main characteristics of baroclinically unstable waves (e.g., the growth rates of unstable waves as function of wavelength) to fundamental atmospheric parameters: the static stability parameter σ₀ which is characterized by temperature lapse rate Γ = −∂T/∂z, and zonal wind vertical shear Λ which, by thermal wind balance, characterizes the meridional temperature gradient. Two classes of waves [55] are considered. The first one is characterized by the Rossby number Ro ≡ U/(fL) ~ 0.1 and the representative horizontal length scale L which is smaller than the Earth’s radius a₀, that is, L/a₀ ~ 0.1. Here U is a horizontal velocity scale and f is the Coriolis parameter. For this class of waves ζ ≫ D, where ζ is the vertical component of relative vorticity and D is the horizontal divergence. Synoptic scale waves belong to this type of motion [58]. The second class, which includes planetary, or ultralong, waves [59], is characterized by Ro ~ 0.01 and L/a₀ ~ 1. For these waves the magnitude of horizontal divergence is comparable with the vertical component of vorticity; that is, ζ ≈ D. To study synoptic scale waves, the Eady-type model is used with uniform zonal wind shear between upper and lower boundaries on an f-plane. In this context parameters σ₀ and Λ are considered to be variables that control the development of baroclinic instability in the atmosphere. Ultralong waves are investigated based on a model with vertically averaged equations [60, 61] with a β-plane approximation. Simplified models such as the Eady model of baroclinic instability and models with vertically averaged equations, despite their simplicity, allow solutions to be obtained that clearly illustrate real physical processes in the atmosphere.

2. Synoptic Scale Baroclinically Unstable Waves

2.1. The Model Equations

We consider the inviscid primitive equation atmospheric model in normalized isobaric coordinates (x, y, ξ) on an f-plane in the following form:

(2)

The state variables of the model are the horizontal velocity vector u = (u,v)^T, the vertical pressure velocity ω ≡ dp/dt, where p is pressure, the geopotential Φ, and the temperature T. The operator ∇≡(∂/∂x, ∂/∂y) is applied to the horizontal coordinates x and y, directed eastward and northward, respectively. The normalized pressure ξ = p/P₀, where P₀ = 1000 hPa is a “standard” pressure approximately equal to the surface pressure, is taken as the vertical coordinate, while the time is denoted by t. Other notations are the diabatic heating rate per unit time per unit mass Q, the gas constant R, the unit vector in the vertical direction k, and the reference state static stability measure S_ξ in the normalized isobaric coordinate system:

(3)

where

is a reference temperature, g is the gravity acceleration, Γ_d is the dry adiabatic lapse rate, and Γ is the reference state lapse rate. We employ the f-plane approximation so that the Coriolis parameter f is a constant f = f₀ = 2Ωsin φ₀ with φ₀ being the latitude of interest. Hereafter we consider only adiabatic process and thus assume zero heating rate Q. The following boundary conditions are used for the pressure velocity:

(4)

The atmospheric reference state, defined by

, and

, is steady and satisfies the following relations:

(5)

where

. By substituting (5) into the set of (2), one can see that (5) is a solution of (2) that describes the zonal flow:

(6)

which matches the specified distribution of the zonally averaged temperature

and represents thermal wind balance. To consider only the baroclinic mechanism of the atmospheric instability, meridional variability of the basic zonal flow is excluded. In other words the barotropic impact on the instability of the basic zonal flow is not taken into account. Therefore we assume that the velocity of the basic zonal flow does not depend on the horizontal y-coordinate; that is,

. Thus, the problem now is the study of the instability of the basic zonal flow (6) with respect to infinitesimal perturbations. For this purpose the system (2) is linearized around the basic state (5). Representing the state variables as

, where

is a basic state and ψ^′ is an infinitesimal perturbation, and taking into account the hydrostatic equations and the thermal wind relationship (6), the linearized system can be written as

(7)

The static stability parameter σ₀ is expressed as

(8)

where α is a specific volume and

is a reference potential temperature. Suppose that

. Applying the method of separation of variables, we assume the solutions of the form

(9)

where

is a function of ξ only, k is a wave number, and c is a phase velocity of perturbations which in general is a complex value: c = c_r + ic_i. After substituting (9) into (7), we can finally obtain the following single equation for

(10)

Similar equations were considered in a number of publications (e.g., [4, 62, 63]). The analytical solution of this equation can be obtained by eliminating gravity waves from the consideration and assuming that σ₀ = const. For this particular case, (10) can be transformed into

(11)

The boundary conditions for

are specified as

(12)

Equation (11), together with boundary conditions (12), represents the eigenvalue problem for the complex phase speed c. The fundamental solutions of (11) are expressed through the Bessel functions of the first and second kinds. With the homogeneous boundary conditions (12), the following two discrete eigenvalues can be obtained [4]:

(13)

where

(14)

The phase velocity c will amplify exponentially if c has an imaginary part c_i. From (13) we can see that this will occur if the discriminant in (13) is less than zero:

(15)

which gives by the Newton’s iteration algorithm the necessary condition for instability: η < η_c ≈ 2.3994. Besides two discrete eigenvalues (13), the eigenvalue problem (11)-(12) has a continuous spectrum of eigenvalues

that are real and therefore can be neglected in the problem of baroclinic instability [4]. The growth rate of unstable waves χ_k ≡ kc_i is calculated by the following expression:

(16)

As we can see from (16), at a given latitude the growth rate χ_k is a function of σ₀ (static stability), Λ_ξ (wind shear), and quantity η that depends on the horizontal wavenumber k and σ₀.

2.2. Impact of Static Stability and Vertical Wind Shear on Baroclinic Instability

Within the Eady problem framework, the static stability parameter σ₀ and the vertical wind shear Λ_ξ represent the main control variables. By varying σ₀ and Λ_ξ, one can obtain estimates of the impact of these parameters on the development of baroclinic instability in the atmosphere. In this research, parameters corresponding to the basic state are given the following values: Λ_ξ = 40 ms⁻¹ [50] and σ₀ = 2 × 10⁻⁶ m² Pa⁻² s⁻² [1]. These parameter values can be used as an approximation to describe the zonal-averaged atmospheric conditions for JJA (June, July, and August) in the SH [50]. The latitude of interest is assumed to be φ₀ = 45 S which gives f₀ = −1.028 × 10⁻⁴ s⁻¹.

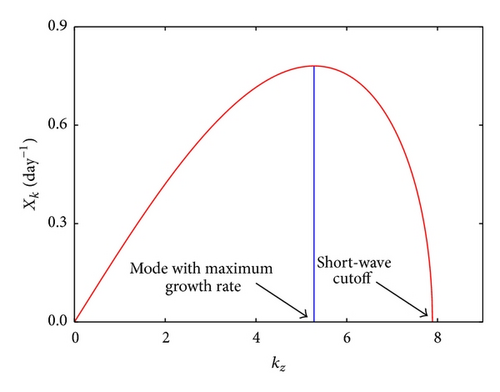
Figure 1 shows plot of Eady growth rate versus zonal wavenumber obtained with (16). The growth rate has a short-wave instability cutoff beyond which waves are stable. Let L_min be the wavelength that corresponds to a short-wave cutoff. Value of L_min can be obtained from (14) when η = η_c which gives L_min = 3592 km. To calculate the wavelength of maximum growth rate L_χmax, one can take ∂χ_k/∂k and set the result equal to zero which gives η = η_m ≈ 1.6061. Then by using (14) we can obtain L_χmax = 5366 km.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Growth rate χ_k versus zonal wavenumber k_z for σ₀ = 2 × 10⁻⁶ m² Pa⁻² s⁻² and Δ_ξ = 40 m s⁻¹.

The influence of the static stability parameter on the wavelength of maximum growth rate L_χmax and the short wave cut-off L_min are shown in Figure 2. In general, an increase in the parameter σ₀ leads to an increase in both L_kcmax and L_min. The functional dependences between L_min and σ₀, and between L_kcmax and σ₀ are almost linear: ±10% departure of static stability parameter Δσ₀ from its nominal value σ₀ = 2.0 × 10⁻⁶ m² Pa⁻² s⁻² results in about ±5% change for both L_kcmax and L_min with respect to the nominal value σ₀. For instance, if Δσ = 0.1 × σ₀, then L_kcmax = 5628 and L_min = 3768 km, and if Δσ = −0.1σ₀, then L_kcmax = 5091 and L_min = 3408 km.

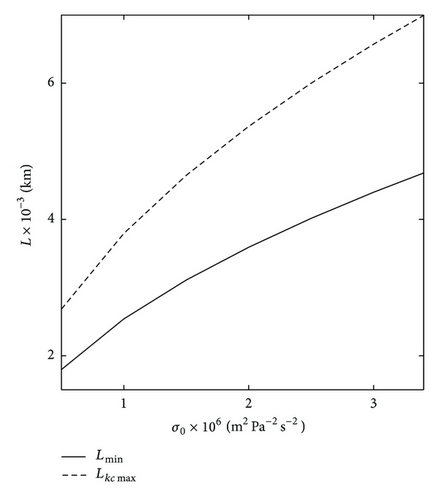
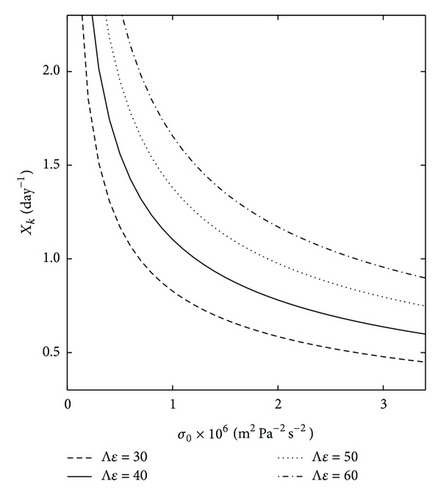
Figure 3 illustrates the growth rate of unstable waves versus the static stability parameter at different values of Λ_ξ. Parameters σ₀ and Λ_ξ influence the growth rate χ_k in the opposite direction: growth rate decreases if σ₀ increases and if Λ_ξ decreases. Note that the decrease of the parameter Λ_ξ indicates the weakening of the intensity of the baroclinic zone, that is, reduction of the MTG. In nature both of these processes take place, which leads to a synergistic effect. For instance, if Λ_ξ decreases by 10% and the static stability parameter increases by 10%, the growth rate χ_k decreases by 14%.

Since χ_k is a nonlinear function of σ₀ (16), to estimate the influence of infinitesimal perturbations in σ₀ on variations in χ_k, the sensitivity function

(17)

and the relative sensitivity function

(18)

can be used. The function S_σ shows changes in χ_k due to variations in σ₀. The relative sensitivity function

is used to compare model parameters to find out what parameter is the most important for a certain percent change in the parameters. Sensitivity functions (17) and (18) are evaluated in the vicinity of some nominal value of the parameter σ₀. We can select several nominal values to cover some range of changes in σ₀. Differentiating (16) with respect to control parameter σ₀, we can obtain the expression for S_σ

(19)

Sensitivity S_σ versus zonal wavenumbers for different values of σ₀ with Λ_ξ = 40 m s⁻¹ are shown in Figure 4. The absolute value of the sensitivity of χ_k with respect to σ₀ exponentially increases with decreasing wavelength. For planetary scale waves (zonal wave numbers 1–4), the absolute value of the sensitivity of χ_k with respect to σ₀ is palpably less than sensitivity for synoptic scale waves (zonal wave numbers ≥5). Absolute and relative sensitivity functions S_σ and

calculated for different values of σ₀ for various zonal wave numbers are shown in Tables 1 and 2, respectively.

Table 1. Absolute sensitivity S_σ as a function of zonal wavenumber k_z for different values of static stability parameter σ₀.

σ₀ m² Pa⁻² s⁻²	Zonal wave number k_z
σ₀ m² Pa⁻² s⁻²	1	2	3	4	5	6	7
1.0 × 10⁻⁶	−0.0157	−0.1251	−0.4175	−0.9772	−1.8879	−3.2470	−5.2005
1.5 × 10⁻⁶	−0.0157	−0.1245	−0.4139	−0.9675	−1.8794	−3.3014	−5.5927
2.0 × 10⁻⁶	−0.0157	−0.1240	−0.4110	−0.9626	−1.8979	−3.4964	−6.9371
2.5 × 10⁻⁶	−0.0157	−0.1234	−0.4088	−0.9629	−1.9509	−3.9665	−23.0031
3.0 × 10⁻⁶	−0.0157	−0.1230	−0.4071	−0.9691	−2.0540	−5.3057

Table 2. Relative sensitivity

as a function of zonal wavenumber k_z for different values of static stability parameter σ₀.

σ₀ m² Pa⁻² s⁻²	Zonal wave number k_z
σ₀ m² Pa⁻² s⁻²	1	2	3	4	5	6	7
1.0 × 10⁻⁶	−0.0062	−0.0250	−0.0575	−0.1057	−0.1735	−0.2692	−0.4095
1.5 × 10⁻⁶	−0.0093	−0.0379	−0.0881	−0.1656	−0.2837	−0.4749	−0.8371
2.0 × 10⁻⁶	−0.0124	−0.0509	−0.1201	−0.2375	−0.4220	−0.8004	−1.9939
2.5 × 10⁻⁶	−0.0156	−0.0642	−0.1539	−0.3087	−0.6071	−1.4399	−31.4243
3.0 × 10⁻⁶	−0.0187	−0.0777	−0.1898	−0.3974	−0.8759	−3.4322

The expression for sensitivity function S_Λ can be easily obtained by differentiating (16) with respect to control parameter Λ_ξ:

(20)

The function S_Λ versus zonal wave number k_z for different σ₀ is plotted in Figure 5. It is clear to see that for a given value of the parameter σ₀ the graph of function S_Λ(k_z) is very much like the classic picture of the growth rates χ_k versus zonal wavenumber k_z [5]. It is interesting that the relative sensitivity function

does not depend on the wavelength (wavenumber) and for all of the unstable waves is equal to unity:

(21)

Since relative sensitivity functions allow direct comparison of the importance of model parameters on the growth rate χ_k, we can see that because

the parameter Λ_ξ (i.e., the meridional temperature gradient) is more important than the static stability parameter σ₀ except for σ₀ > 2 × 10⁻⁶ m² Pa⁻² s⁻² for waves with k_z ≥ 6 (see Table 2). Wherever the midlatitude values in Table 2 are less than one, the growth rate is more sensitive to the meridional temperature gradient (i.e., Λ_ξ) than the static stability (σ₀).

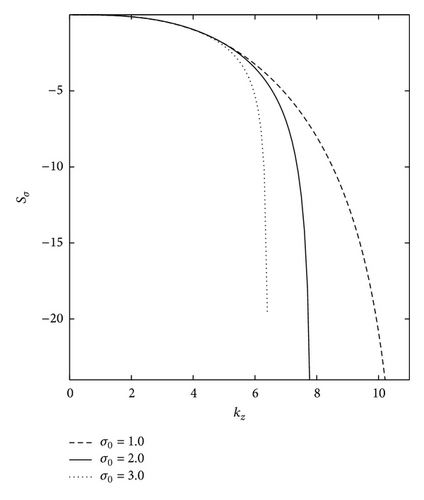
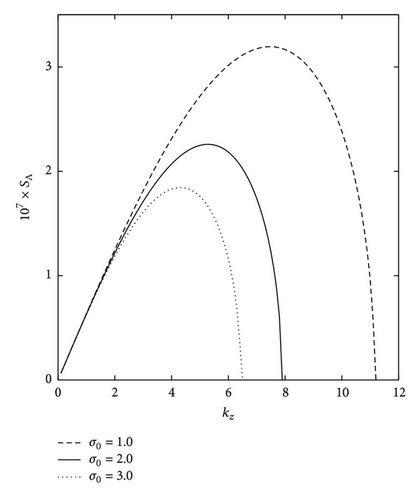
The obtained results are consistent with observations [50, 51, 54]: an increase in static stability and a decrease of the MTG have occurred over the past few decades in some areas of the SH, which has led to a decrease in the growth rate of baroclinic unstable waves, a shift of the spectrum of unstable waves in the long wavelength part of spectrum, and a weakened intensity of cyclogenesis. Naturally, these changes affect favourable conditions for the development of baroclinic instability and the essential features of weather patterns over large territories, particularly over Australia.

3. Planetary Scale Waves

To study the influence of the static stability parameter on the dynamics of planetary scale (ultralong) waves, a thin film approximation is applied. This approximation employs a specific averaging technique over the vertical coordinate to the system of primitive equations [60]. As a result, a two-dimensional set of equations can be obtained that describes the dynamics of a two-dimensional baroclinic film. These equations reproduce all the wavelike solutions that correspond to the main weather-forming modes of three-dimensional models and therefore can be used in theoretical studies of large-scale dynamic processes in the atmosphere. The system of vertically averaged equations can be written as [60]

(22)

where π = p_s/P₀. For instance, if the original primitive equations are written in the Phillips’ vertical coordinate system σ = p/p_s [64], the operator for vertical averaging is introduced as

and state variables are represented as

. Equations (22) are obtained by neglecting the orography and terms

, and

[65]. A detailed linear analysis of the vertically averaged equation (22) is represented in [60]. In particular, two types of wave solutions were found: fast waves that propagate westward and slow waves that move eastward. Within the framework of this model, ultralong waves are always neutral for any vertically averaged zonal wind velocity. Indeed, linearizing (22) around the following basic state:

(23)

and assuming the beta plane approximation f = f₀ + βy, where β = (2Ω/a₀)cos φ₀, and representing the solution in the form (9), one can finally obtain under different asymptotics the following expressions for four wave solutions [60]:

(a)
acoustic waves
(24)
(b)
Rossby wave
(25)
(c)
baroclinic wave
(26)

Here

and κ = R/c_p. These results however are valid only for the specific case of a neutral atmosphere with Γ = Γ_d [60, 61]. To take into account the atmospheric static stability on the behaviour of ultralong waves the polytropic model of the atmosphere can be used for which

(27)

where T₀ is the temperature at the surface and Γ is a vertical temperature gradient. Integrating (27) with respect to vertical coordinate, we can obtain

[60]. Assuming the geostrophic approximation on a β-plane, the set of vertically averaged equations can be written as [61]

(28)

Here α₁ = 1 + R(Γ/g), α₂ = 1 + 2R(Γ/g), α₃ = R(Γ/g), α₄ = 1 − (Γ/Γ_d), and the operator (A, B) = (∂A/∂x)(∂B/∂y) − (∂A/∂y)(∂B/∂x). The basic state is defined as a stationary solution of system (28) for which

(29)

or in other words

(30)

Linearizing (28) around the basic state (30), the following cubic characteristic equation can be obtained in which the second order terms are neglected [61]:

(31)

where

and

. If the discriminant of this equation is positive, then the wave solution is unstable. The domain of zonal flow instability can be found numerically (see diagram in [61]). In Figure 6, we reproduce only for the 1st quadrant of a Cartesian plane the domain of instability calculated as a function of vertically averaged zonal wind velocity u₀ and dimensionless temperature lapse rate Γ/Γ_d.

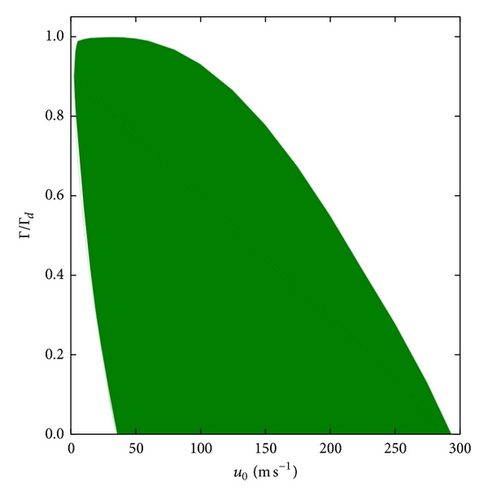
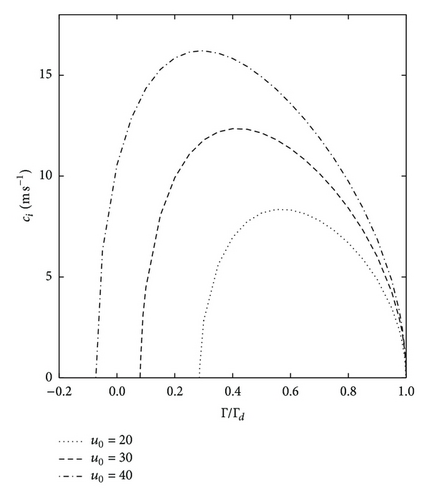
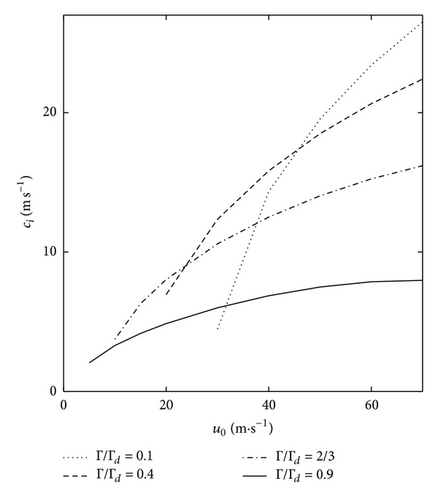
The imaginary part of phase velocity c_i which characterises the growth rate of unstable waves χ_k ≡ kc_i is displayed in Figure 7 as a function of dimensionless temperature lapse rate Γ/Γ_d for different values of vertically averaged zonal wind velocity u₀. A maximum phase velocity c_i exists for given values of u₀; that is, dependent on the ratio of Γ/Γ_d. For instance, if u₀ = 20 m s⁻¹ then the maximum value (c_i) _max ≈ 8.34 m s⁻¹ is reached at Γ/Γ_d ≈ 0.55. Figure 6 shows that increasing vertically averaged zonal wind u₀ is associated with increasing c_i. This is further evident in Figure 8, which shows c_i as a function of u₀ for a range of Γ/Γ_d values. The lower Γ/Γ_d and the larger c_i, that is, c_i, increases with decreasing static stability.

4. Concluding Remarks

We have studied theoretically the impact of variations in the static stability parameter σ₀ and zonal wind shear Λ_ξ on the characteristics of baroclinically unstable waves of synoptic scales using Eady-type model with the uniform Λ_ξ between upper and lower boundaries on an f-plane. Quantitative estimates of variations in σ₀ and Λ_ξ on the growth rate χ_k, wavelength of maximum growth rate L_χmax, and short-wave cutoff L_min were obtained.

Analytical expressions are derived for sensitivity functions for the growth rate χ_k with respect to variations in static stability parameter and wind shear velocity. These expressions allow estimating to a first-order approximation the influence of changes in σ₀ and Λ_ξ on χ_k. Analytical expressions for relative sensitivity functions allow estimating the significance of variations in σ₀ and Λ_ξ on the growth rate of baroclinically unstable waves with a given zonal wave number.

To study the impact of variations in atmospheric static stability and zonal wind velocity on the instability of planetary scale waves, the model with vertically averaged primitive equations with β-plane approximation was applied. As control parameters, we have used dimensionless temperature lapse rate Γ/Γ_d and vertically averaged zonal wind velocity u₀. We have estimated the influence of Γ/Γ_d and u₀ on the imaginary part of phase speed c_i, which was used as a measure of instability.

The obtained results are qualitatively consistent with changes in the essential weather patterns that occurred over the last several decades in some areas of the SH and, in particular, over Australia (e.g., [49, 50, 52–54]). Climate change results suggest SH midlatitude static stability σ₀ may increase and the MTG (the vertical wind shear Λ_ξ) may decrease, which according to our linear theoretical models leads to a slowing of the growth rate of baroclinic unstable waves χ_k and an increasing wavelength of baroclinic unstable wave with maximum growth rate L_χmax, that is, a spectrum shift of unstable waves towards longer wavelengths. These might affect the favourable conditions for the development of baroclinic instability and, therefore, the rate of cyclogenesis and a reduction in cyclone intensity. The obtained sensitivity functions demonstrate that waves belonging to the short-wave part of the spectrum of unstable waves are more sensitive to changes in the static stability parameter than waves belonging to the long-wave part of the spectrum.

To obtain more realistic estimates of the sensitivity of the growth rate of unstable waves with respect to static stability parameter and MTG, numerical modeling based on a full GCM is required. It is hoped to carry out such work in the future.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

The authors thank Dr. I. Pisnichenko for clarification of certain questions relevant to this paper.

References

1 Holton J. R., An Introduction to Dynamic Meteorology, 1992, 3rd edition, Academic Press.
Google Scholar
2 Vallis G. K., Atmospheric and Oceanic Fluid Dynamics, 2006, Cambridge University Press.
Google Scholar
3 Mak M., Atmospheric Dynamics, 2011, Cambridge University Press.
Google Scholar
4 Dymnikov V. P., Stability and Predictability of the Large Scale Atmospheric Processes, 2007, Institute of Numerical Mathematics of the Russian Academy of Sciences, Moscow, Russia.
Google Scholar
5 Charney J. G., The dynamics of long waves in baroclinic westerly current, Journal of Meteorology. (1947) 4, 135–162.
Google Scholar
6 Eady E. T., Long waves and cyclone waves, Tellus. (1949) 1, 33–52.
Google Scholar
7 Pierrehumbert R. T. and Swanson K. L., Baroclinic instability, Annual Review of Fluid Mechanics. (1995) 27, no. 1, 419–467, 2-s2.0-0028797583.
Google Scholar
8 Gall R., A comparison of linear instability theory with the eddy statistics of a general circulation model, Journal of the Atmospheric Sciences. (1976) 33, no. 3, 349–373, 2-s2.0-0016926285.
Google Scholar
9 Held I. M., T. Schneider and A. Sobel, Progress and problems in large-scale atmospheric dynamics, The Global Circulation of the Atmosphere, 2007, Princeton University Press, Princeton, NJ, USA, 1–21.
Google Scholar
10 Farrell B., Modal and non-modal baroclinic waves, Journal of the Atmospheric Sciences. (1984) 41, no. 4, 668–673, 2-s2.0-0021639725.
Google Scholar
11 Tippett M. K., Transient moist baroclinic instability, Tellus A. (1999) 51, no. 2, 273–288, 2-s2.0-0032766976.
Google Scholar
12 Hodyss D. and Grotjahn R., Nonmodal and unstable normal mode baroclinic growth as a function of horizontal scale, Dynamics of Atmospheres and Oceans. (2003) 37, no. 1, 1–24, 2-s2.0-0037677517.
Google Scholar
13 Pedlosky J., Finite amplitude baroclinic waves, Journal of the Atmospheric Sciences. (1970) 27, no. 1, 15–30, 2-s2.0-0014718485.
Google Scholar
14 Romea R. D., The effects of friction and beta on finite amplitude baroclinic waves, Journal of the Atmospheric Sciences. (1977) 34, 1689–1695.
Google Scholar
15 Pedlosky J., Finite-amplitude baroclinic waves at minimum critical shear, Journal of the Atmospheric Sciences. (1982) 39, no. 3, 555–562, 2-s2.0-0020379896.
Google Scholar
16 Warn T. and Gauthier P., Potential vorticity mixing by marginally unstable baroclinic disturbances, Tellus A. (1989) 41, no. 2, 115–131, 2-s2.0-0024568217.
Google Scholar
17 Simmons A. J. and Hoskins B. J., The lifecycles of some nonlinear waves, Journal of the Atmospheric Sciences. (1978) 35, 414–432.
Google Scholar
18 Simmons A. J. and Hoskins B. J., Barotropic influences of the growth and decay of nonlinear baroclinic waves, Journal of the Atmospheric Sciences. (1980) 37, 1679–1684.
Google Scholar
19 Feldstein S. B. and Held I. M., Barotropic decay of baroclinic waves, Journal of the Atmospheric Sciences. (1989) 46, 1679–1684, 2-s2.0-0024903432.
Google Scholar
20 Thorncroft C. D., Hoskins B. J., and McIntyre M. E., Two paradigms of baroclinic-wave life-cycle behaviour, Quaterly Journal. (1993) 119, no. 509, 17–55, 2-s2.0-0027444406.
Google Scholar
21 Phillips N. A., A simple three-dimensional model for the study of largescale extratropical flow patterns, Journal of Meteorology. (1951) 8, 381–394.
Google Scholar
22 Phillips N. A., Energy transformations and meridional circulations associated with simple baroclinic waves in a two-level, quasi-geostrophic model, Tellus. (1954) 6, 273–286.
Google Scholar
23 Polvani L. M. and Pedlosky J., The effect of dissipation on spatially growing nonlinear baroclinic waves, Journal of the Atmospheric Sciences. (1988) 45, no. 14, 1977–1989, 2-s2.0-0024190980.
Google Scholar
24 Shepherd T. G., Nonlinear saturation of baroclinic instability. Part I: the two-layer model, Journal of the Atmospheric Sciences. (1988) 45, no. 14, 2014–2025, 2-s2.0-0024191536.
Google Scholar
25 Balasubramanian G. and Yau M. K., Baroclinic instability in a two-layer model with parameterized slantwise convection, Journal of the Atmospheric Sciences. (1994) 51, no. 7, 971–990, 2-s2.0-0028582405.
Google Scholar
26 Wiin-Nielsen A., On the structure of atmospheric waves in middle latitudes, Atmosfera. (2003) 16, no. 2, 83–102, 2-s2.0-0041471438.
Google Scholar
27 Holm D. D. and Wingate B. A., Baroclinic instabilities of the two-layer quasigeostrophic alpha model, Journal of Physical Oceanography. (2005) 35, no. 7, 1287–1296, 2-s2.0-24944522299, https://doi.org/10.1175/JPO2741.1.
Google Scholar
28 Egger J., Baroclinic instability in the two-layer model: interpretations, Meteorologische Zeitschrift. (2009) 18, no. 5, 559–565, 2-s2.0-77949346599, https://doi.org/10.1127/0941-2948/2009/0405.
Google Scholar
29 Lamberts J., Lapeyre G., and Zeitlin V., Moist versus dry baroclinic instability in a simplified two-layer atmospheric model with condensation and latent heat release, Journal of the Atmospheric Sciences. (2012) 69, 1405–1426.
Google Scholar
30 Frierson D. M. W., Robust increases in midlatitude static stability in simulations of global warming, Geophysical Research Letters. (2006) 33, no. 24, 2-s2.0-34548016274, https://doi.org/10.1029/2006GL027504, L24816.
Google Scholar
31 Hall N. M. J., Hoskins B. J., Valdes P. J., and Senior C. A., Storm tracks in a high-resolution GCM with doubled carbon dioxide, Quarterly Journal. (1994) 120, no. 519, 1209–1230, 2-s2.0-0028667313.
Google Scholar
32 Feldstein S. B., The recent trend and variance increase of the annular mode, Journal of Climate. (2002) 15, no. 3, 88–94, 2-s2.0-0036464981.
Google Scholar
33 Marshall G. J., Trends in the southern annular mode from observations and reanalyses, Journal of Climate. (2003) 16, 4134–4143.
Web of Science® Google Scholar
34 Ostermeier G. M. and Wallace J. M., Trends in the North Atlantic Oscillation-Northern Hemisphere annular mode during the twentieth century, Journal of Climate. (2003) 16, no. 2, 336–341, 2-s2.0-0141453104.
Google Scholar
35 Thompson D. W. J. and Solomon S., Interpretation of recent Southern Hemisphere climate change, Science. (2002) 296, no. 5569, 895–899, 2-s2.0-0037012924, https://doi.org/10.1126/science.1069270.
Google Scholar
36 Lambert S. J., The effect of enhanced greenhouse warming on winter cyclone frequencies and strengths, Journal of Climate. (1995) 8, no. 5, 1447–1462, 2-s2.0-0029537410.
Google Scholar
37 Lunkeit F., Fraedrich K., and Bauer S. E., Storm tracks in a warmer climate: sensitivity studies with a simplified global circulation model, Climate Dynamics. (1998) 14, no. 11, 813–826, 2-s2.0-0032468740, https://doi.org/10.1007/s003820050257.
Google Scholar
38 Lorenz D. J. and Hartmann D. L., Eddy-zonal flow feedback in the Southern Hemisphere, Journal of the Atmospheric Sciences. (2001) 58, no. 21, 3312–3327, 2-s2.0-0035513347.
Google Scholar
39 Geng Q. and Sugi M., Possible change of extratropical cyclone activity due to enhanced greenhouse gases and sulphate aerosols: study with a high-resolution AGCM, Journal of Climate. (2003) 16, 2262–2274.
Google Scholar
40 Fyfe J. C., Extratropical Southern Hemisphere cyclones: harbingers of climate change, Journal of Climate. (2003) 16, 2802–2805.
Google Scholar
41 Yin J. H., A consistent poleward shift of the storm tracks in simulations of 21st century climate, Geophysical Research Letters. (2005) 32, no. 18, 1–4, 2-s2.0-27744475160, https://doi.org/10.1029/2005GL023684, L18701.
Google Scholar
42 Lambert S. J. and Fyfe J. C., Changes in winter cyclone frequencies and strengths simulated in enhanced greenhouse warming experiments: results from the models participating in the IPCC diagnostic exercise, Climate Dynamics. (2006) 26, no. 7-8, 713–728, 2-s2.0-33645990919, https://doi.org/10.1007/s00382-006-0110-3.
Google Scholar
43 Gastineau G. and Soden B. J., Model projected changes of extreme wind events in response to global warming, Geophysical Research Letters. (2009) 36, no. 10, L10810, 2-s2.0-67651098659, https://doi.org/10.1029/2009GL037500.
Google Scholar
44 Wu Y., Ting M., Seager R., Huang H.-P., and Cane M. A., Changes in storm tracks and energy transports in a warmer climate simulated by the GFDL CM2.1 model, Climate Dynamics. (2011) 37, no. 1, 53–72, 2-s2.0-79959783379, https://doi.org/10.1007/s00382-010-0776-4.
Google Scholar
45 Bengtsson L., Hodges K. I., and Roeckner E., Storm tracks and climate change, Journal of Climate. (2006) 19, no. 15, 3518–3543, 2-s2.0-33646372857, https://doi.org/10.1175/JCLI3815.1.
Google Scholar
46 Smith I., An assessment of recent trends in Australian rainfall, Australian Meteorological Magazine. (2004) 53, no. 3, 163–173, 2-s2.0-7044281928.
Google Scholar
47 Nicholls N., Detecting, Understanding and Attributing Climate Change, 2007, Australian Greenhouse Office Publication.
Google Scholar
48 Bates B. C., Hope P., Ryan B., Smith I., and Charles S., Key findings from the Indian Ocean Climate Initiative and their impact on policy development in Australia, Climatic Change. (2008) 89, no. 3-4, 339–354, 2-s2.0-48749106702, https://doi.org/10.1007/s10584-007-9390-9.
Google Scholar
49 Frederiksen J. S. and Frederiksen C. S., Decadal changes in Southern Hemisphere winter cyclogenesis, CSIRO Marine and Atmospheric Research Paper, 2005, no. 002.
Google Scholar
50 Frederiksen J. S. and Frederiksen C. S., Interdecadal changes in southern hemisphere winter storm track modes, Tellus A. (2007) 59, no. 5, 599–617, 2-s2.0-34548718204, https://doi.org/10.1111/j.1600-0870.2007.00264.x.
Google Scholar
51 Frederiksen J. S., Frederiksen C. S., and Osbrough S. L., Modelling of changes in Southern Hemisphere weather systems during the 20th century, Proceedings of the 18th World IMACS Congress and International Congress on Modelling and Simulation, July 2009, Cairns, Australia, 2562–2568, 2-s2.0-80052978652.
Google Scholar
52 Frederiksen J. S., Frederiksen C. S., Osbrough S. L., and Sisson J. M., I. Jupp, P. Holper, and W. Cai, Causes of changing Southern Hemispheric weather systems, Managing Climate Change, 2010, CSIRO Publishing, 85–98.
Google Scholar
53 Frederiksen J. S., Frederiksen C. S., Osbrough S. L., and Sisson J. M., Changes in Southern Hemisphere rainfall, circulation and weather systems, Proceedings of the 19th International Congress on Modelling and Simulation (MODSIM ′11), December 2011, Perth, Australia, 2712–2718, 2-s2.0-84858815857.
Google Scholar
54 Frederiksen C. S., Frederiksen J. S., Sisson J. M., and Osbrough S. L., Observed and projected changes in the annual cycle of Southern Hemisphere baroclinicity for storm formation, Proceedings of the 19th International Congress on Modelling and Simulation (MODSIM′ 11), December 2011, Perth, Australia, 2719–2725, 2-s2.0-84858811562.
Google Scholar
55 Phillips N. A., Geostrophic motion, Reviews of Geophysics. (1963) 1, no. 2, 123–176.
Google Scholar
56 Bordi I., Fraedrich K., Lunkeit F., and Sutera A., Tropospheric double jets, meridional cells, and eddies: a case study and idealized simulations, Monthly Weather Review. (2007) 135, no. 9, 3118–3133, 2-s2.0-34848902633, https://doi.org/10.1175/MWR3464.1.
Google Scholar
57 Bordi I., Fraedrich K., Ghil M., and Sutera A., Zonal flow regime changes in a GCM and in a simple quasigeostrophic model: the role of stratospheric dynamics, Journal of the Atmospheric Sciences. (2009) 66, no. 5, 1366–1383, 2-s2.0-69849090935, https://doi.org/10.1175/2008JAS2771.1.
Google Scholar
58 Charney J. G., On the scale of atmospheric motions, Geofysiske Publikasjoner. (1948) 17, no. 2, 3–17.
Google Scholar
59 Burger A., Scale consideration of planetary motions of the atmosphere, Tellus. (1958) 10, 195–205.
Google Scholar
60 Pisnichenko I. A., Ultralong-wave dynamics in a two-dimensional baroclinic atmosphere model, Atmospheric and Oceanic Physics. (1980) 16, no. 9, 883–892, 2-s2.0-0019057099.
Google Scholar
61 Pisnichenko I. A., Influence variable static stability on the dynamics of ultralong waves in two-dimensional baroclinic model of the atmosphere, Atmospheric and Oceanic Physics. (1983) 19, no. 11, 1223–1226.
Google Scholar
62 Wiin-Nielsen A., On barotropic and baroclinic models, with special emphasis on ultra-long waves, Monthly Weather Review. (1959) 87, 171–183.
Google Scholar
63 Bin Wang B. W. and Barcilon A., Moist stability of a baroclinic zonal flow with conditionally unstable stratification, Journal of the Atmospheric Sciences. (1986) 43, no. 7, 705–719, 2-s2.0-0022848990.
Google Scholar
64 Phillips N. A., A coordinate system having some special advantages for numerical forecasting, Journal of Meteorology. (1957) 14, 184–185.
Web of Science® Google Scholar
65 Alishaev D. M., Dynamics of a two-dimensional baroclinic atmosphere, Atmospheric and Oceanic Physics. (1980) 16, no. 2, 99–107, 2-s2.0-0018983962.
Google Scholar

Citing Literature

All articles

The Sensitivity of Characteristics of Large Scale Baroclinic Unstable Waves in Southern Hemisphere to the Underlying Climate

Abstract

1. Introduction

2. Synoptic Scale Baroclinically Unstable Waves

2.1. The Model Equations

2.2. Impact of Static Stability and Vertical Wind Shear on Baroclinic Instability

3. Planetary Scale Waves

4. Concluding Remarks

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

The Sensitivity of Characteristics of Large Scale Baroclinic Unstable Waves in Southern Hemisphere to the Underlying Climate

Abstract

1. Introduction

2. Synoptic Scale Baroclinically Unstable Waves

2.1. The Model Equations

2.2. Impact of Static Stability and Vertical Wind Shear on Baroclinic Instability

3. Planetary Scale Waves

4. Concluding Remarks

Conflict of Interests

Acknowledgment

References

Citing Literature

Figures

References

Related

Information