Abstract and Applied Analysis
Volume 2013, Issue 1 950396
Research Article
Open Access

Global Stability Analysis and Optimal Control of a Harvested Ecoepidemiological Prey Predator Model with Vaccination and Taxation

Chao Liu, 

Corresponding Author

Chao Liu

Institute of Systems Science, Northeastern University, Shenyang 110004, China northeastern.edu

State Key Laboratory of Integrated Automation of Process Industry, Northeastern University, Shenyang 110004, China northeastern.edu

Search for more papers by this author
Qingling Zhang, 

Qingling Zhang

Institute of Systems Science, Northeastern University, Shenyang 110004, China northeastern.edu

State Key Laboratory of Integrated Automation of Process Industry, Northeastern University, Shenyang 110004, China northeastern.edu

Search for more papers by this author
Jinna Li, 

Jinna Li

Shenyang Institute of Automation, Chinese Academy of Sciences, Shenyang 110004, China cas.cn

Search for more papers by this author
First published: 30 July 2013
https://doi.org/10.1155/2013/950396
Citations: 2
Academic Editor: Luca Guerrini

Abstract

We propose an ecoepidemiological prey predator model, where selective harvest effort on predator population is considered. Vaccination and taxation are introduced as control instruments, which are utilized to control number of susceptible prey population and protect predator population from overexploitation, respectively. Conditions which influence nonnegativity and boundedness of solutions are studied. Global stability analysis around disease-free equilibrium is discussed based on robust Bendixson criterion, which is theoretically beneficial to studying coexistence and interaction mechanism of population within harvested ecoepidemiological system. By using Pontryagin’s maximum principle, an optimal control strategy is derived to maximize the total discounted net economic revenue to society as well as protect prey population from infectious disease. Numerical simulations are carried out to show the consistency with theoretical analysis.

1. Introduction

In the natural world, prey predator ecosystem with infectious disease is a well-studied ecological phenomenon. Generally, species within prey predator ecosystem does not exist alone. While species spreads the disease, it also competes with the other species for space or food, or is predated by other species. Kermack-Mc kendrick made the pioneering work on (susceptible-infective-removal-susceptible) SIRS [1]. Along with the line of this research, mathematical epidemiology has become an important subject of research in recent decades, where the evolution of a disease which gets transmitted upon contact is described. In the work done by Hadeler and Freedman [2], a prey predator model where the prey is infected by a parasite and in turn infects the predator with the parasite. Thereafter, plenty of papers were made to investigate prey predator system with infection in the prey. Arino et al. [3, 4] observed that the introduction of an infected population in the classical ratio-dependent predator-prey model may act as a biological control to save the population from extinction. Hethcote et al. [5, 6] considered the effects of disease-induced mortality or disease-reduced reproduction in regulating natural populations, decreasing their population sizes, reducing their natural fluctuations, or causing destabilization of equilibria into oscillations of the population states. In the work done by Haque and Venturino [7], the mixed terms of the underlying demographic model describing the mass action law of populations affect each other, and Holling-type functions are taken into account [8]. In the above mentioned work, by performing dynamic analysis with the help of linear approximation to model systems that consist of nonlinear equations, it concludes that it is of importance from ecological and mathematical points of view to study ecological systems subject to epidemiological factors.

Recently, an eco-epidemiological model consisting of susceptible prey, infected prey, and predator is proposed and analyzed in [9]. It is assumed that the predation functional response (trophic function) allows Holling type II (Michaelis-Menten kinetics). From the above assumptions model system can be expressed as follows:
()
where s(t) is the susceptible prey population densities per hectare and i(t) is the infected prey population densities per hectare, so that the total prey population densities at any time t per hectare is s(t) + i(t), and it is assumed that the infected prey population contributes with the susceptible prey population to the prey population growth towards the environment carrying capacity. Consequently, the susceptible prey population grows according to a logistic law with carrying capacity k > 0 and intrinsic growth rate constant r > 0 involving the whole prey population (susceptible prey and infected prey population), which is best regarded as a purely descriptive equation. The transmission rate among the susceptible prey population and the infected prey population follows the simple law of mass action cs(t) i(t) for all t > 0, where c > 0 denotes the transmission coefficient. The infectious disease spreads among the prey population only and that disease is not genetically inherited. The infected prey population does not recover or become immune. p(t) is the predator population densities per hectare which is assumed to feed on both the susceptible and the infected prey population. e denotes the natural death rate of the infected prey populations; f is the death rate of the predator population; d1 and d2 which are within the interval (0,1) are the conversion rate of the susceptible and the infected prey population to the predator population, respectively. a1 and a2 are the searching efficiency constants or equivalently the predation rates on the susceptible and the infected prey populations, respectively. b1 and b2 are the positive constants.

It is well known that harvesting has a strong impact on the dynamic evolution of a population. Evidence shows that many species have already become extinct and many others are at the verge of extinction due to several natural or man-made reasons like over exploitation, indiscriminate harvesting and mismanagement of natural resources, and so forth. The severity of this impact that may range from rapid depletion to complete preservation of a population depends on the implemented harvesting agency [10, 11]. Due to practical and economic utilization, biological resources in the prey predator system are extensively harvested nowadays. Furthermore, exploitation of biological resources has been increased by people’s multifarious material needs, which attracts a global concern to protect the limited biological resources. Therefore, regulation of exploitation of biological resources has become a problem of major concern in view of dwindling resource stocks and the deteriorating environment. It is necessary to establish a constructive management of commercial exploitation of the biological resources. The techniques and issues associated with bioeconomic exploitation have been discussed in details by Clark [12]. Taxation, license fees, lease of property rights, seasonal harvesting, and so forth are usually considered as possible governing instruments in regulation for harvesting as well as regulatory mechanisms to keep the damage to the ecosystem minimal. Out of these regulating options, taxation is considered to be superior because of its economic flexibility [13], and economists are particularly attracted to taxation because a competitive system can be better maintained under taxation rather than other regulatory methods. There has been considerable interest in the modeling of harvesting of biological resources in recent decades, where harvest effort is considered to be a dynamic variable, and optimal harvesting policies with taxation are discussed. Ganguly and Chaudhuri [14], Krishna et al. [15], and Dubey et al. [16, 17] investigated the optimal harvesting of a class of models of a single fishery species with taxation as a control. Kar [18, 19] studied the optimal tax policies for harvesting of the prey predator system.

Recently, stimulated by new analytical and numerical findings, scholars have found interest to discuss the applications of optimal control theory to eco-epidemiological model, which can be found in [20–22]. Mathematical modelling of infectious disease with application of optimal control theory is investigated in [23–25], where vaccination cost is considered to discuss associated optimal problems. It should be noted that harvesting issues are also considered in eco-epidemiological model [26, 27], where dynamical behaviour and impulsive harvesting control are investigated. However, to authors’ best knowledge, optimal control strategy associated with maximum net economic revenue of harvesting and vaccination cost in eco-epidemiological model has not been investigated in related research.

In this paper, a harvested eco-epidemiological prey predator system is established in the second section. We extend the work done in [9] by incorporating the harvest effort on predator population. Based on superiority of taxation control in regulating harvesting and effectiveness of vaccination in protecting population from infectious disease introduced above, vaccination is introduced to control number of susceptible prey population, and taxation is chosen to regulate exploitation of biological resource within the harvested eco-epidemiological prey predator system. In the third section, nonnegativity and boundedness of solutions of the proposed model are discussed. In the fourth section, global stability analysis of model system around disease-free equilibrium is studied based on robust Bendixson criterion. Furthermore, by taking taxation and vaccination control as time dependent, an optimal strategy associated with net harvesting revenue and vaccination cost is investigated by using Pontryagin’s maximum principle in the fifth section. It is assumed that vaccination cost is considered and exploitation of the predator species is regulated by an authority by imposing taxation per unit biomass of the harvested predator, and the imposition of taxation acts as a deterrent to control harvesting. We aim to find an optimal strategy which guarantees a lasting exploitation of the biological resource and maximize the total discounted net economic revenue to society as well as protect prey population from infectious disease. Numerical simulations are provided to support the analytical findings obtained in this paper. Finally, this paper ends with a conclusion.

2. Model Formulation

In 1954, Gordon [28] proposed the economic theory of a common property resource, which studies the effect of harvest effort on ecosystem from an economic perspective. It is well known that the harvested predator is usually sold as commodity in the market in order to achieve economic interest, which implies that the unit price of harvested population is influenced by the fluctuation of supply and demand for harvested population in the market, and the unit cost of harvest effort depends on fecundity of harvested population [12, 28]. Consequently, the unit price and unit cost are not always constant, but time varying. Assuming that there is always constant demand for harvested predator, then v1(t) the unit price of harvested predator and v2(t) the unit cost of harvest effort can be expressed as
()
respectively, where E(t) represents the harvest effort on predator population p(t) at any time t > 0, h, σ, β and g are all positive constants. To conserve the population in the harvested eco-epidemiological prey predator system, the regulatory agency imposes a tax σ > 0 per unit biomass of the predator, and σ < 0 denotes the subsidies given to the harvest effort. E(t)p(t) denotes supply amount of harvested predator into the market.
By simple computation, it can be found that the unit price will decrease if the supply of harvested predator is larger than the demand for harvested predator; on the other hand, the unit price will increase if the supply of harvested predator cannot meet the demand for harvested predator, and the maximum unit price is (h − σ)/β. It is also obvious that
()
which imply that the unit cost of harvest effort is inversely proportional to the population density of harvested predator. More richer the population density of harvested predator becomes, more lower the unit cost of harvest effort is; on the other hand, the unit cost of harvest effort will increase if the population density of harvested predator becomes relatively rare.
According to the above analysis, a harvested eco-epidemiological prey predator model with vaccination and taxation is proposed based on (1) and (2), which can be governed by the following differential equations:
()
The initial conditions of model system (4) are given as follows:
()
where α describes stiffness parameter measuring the strength of reaction of harvest effort and susceptible prey population is vaccinated at vaccination rate u. Other parameters that share the same interpretations are mentioned in (1) and (2).

Remark 1. It should be noted that it is assumed that harvesting issue in model system (4) does not affect the growth of prey population (susceptible prey and infected prey) directly. Effect of harvest effort and harvesting regulation on prey population is biologically functioned through the predator population.

Remark 2. It is further assumed that vaccination rate u such that constraint 0 ≤ u < 1 for any time, which vividly reflects the fact that vaccination on the entire susceptible prey population is impossible.

3. Nonnegativity and Boundedness of Solution

Theorem 3. All solutions of model system (4) with initial conditions are nonnegative.

Proof. The model system (4) can be interpreted as the matrix form:

()
where X(t) = (s(t), i(t), p(t), E(t)) T ∈ ℝ4 and H(X(t)) is given as follows:
()
Let be the nonnegative octant in ℝ4, then is locally Lipschitz and satisfy the condition .

Due to lemma in [29] and [30, Theorem A.4], any solution of the model system (4) with nonnegative initial conditions exist uniquely, and each component of the solution remains within the interval [0, A0) for some A0 > 0. Standard and simple arguments show that solutions of model system (4) always exist and stay nonnegative. Hence, this completes the nonnegativity of the solutions of model system (4).

Theorem 4. If h − σ > 0 and d1 ≥ d2, then all solutions of model system (4) are bounded within a region Ω for all t > 0,

()

On the other hand, if h − σ > 0 and d1 < d2, then all solutions of model system (4) are bounded within a region Ω for all t > 0,

()
where w1(t) = s(t) + i(t), w2(t) = d1s(t) + d2i(t) + p(t), and m1 = min {e, u, f}.

Proof. Firstly, we consider the first equation of model system (4). We have

()
which implies that
()

Now, defining the function w1(t) = s(t) + i(t) by calculating the time derivative of w1(t) along the solutions of model system (4), we get

()
By utilizing the standard comparison principle, it follows that
()

Furthermore, by using nonnegativity of solution of model system (4), if h − σ > 0, then it derives that

()
which implies that
()

Let w2(t) = d1s(t) + d2i(t) + p(t), and by calculating the time derivative of w2(t) along the solutions of model system (4), it can be obtained that

()

Hence, it derives that

()
where m1 = min {e, u, f}.

Consequently, If h − σ > 0 and d1 ≥ d2, then all solutions of model system (4) are bounded within a region Ω for all t > 0,

()

On the other hand, if h − σ > 0 and d1 < d2, then all solutions of model system (4) are bounded within a region Ω for all t > 0,

()

Remark 5. Since the components (s(t),  i(t),  and  p(t)) of solution of model system (4) represent the population in the harvested eco-epidemiological prey predator system, boundedness reveals a natural restriction to growth as a consequence of limited resources. Especially, boundedness of i(t) epidemiologically interprets infectious disease in prey population, it can not spread without limitation, and prey population may not die out due to rampant spread of infectious disease. Furthermore, with the purpose of maintaining the sustainable development of prey predator system, the harvesting can not increase without any restriction, which is reflected by the boundedness of E(t). It is of inspiration for people to regulate the harvesting effort by means of economic instrument.

4. Global Stability Analysis around Disease-Free Equilibrium

In this section, global stability analysis around disease-free equilibrium is discussed. It is utilized to discuss stability mechanism of model system due to variation of taxation and vaccination control. It should be noted that we only concentrate on the dynamical behavior and stability analysis around disease-free equilibrium, since biological interpretation of disease-free equilibrium implies that susceptible prey, predator population all exist under infectious disease-free environment, only susceptible prey population is predated and harvest effort on predator population exists, which are relevant to our main study in this paper.

For simplicity, model system (4) is nondimensionalized with the following scaling: S = s/k,  I = i/k,  P = a1p/r,  Y = E/r,  T = rt. By using these quantities, model system (4) can be transformed into a dimensionless form as follows:
()
where c1 = ck/r, e1 = e/r, a3 = a2/a1, b3 = b1k, b4 = b2k, f1 = f/r, d3 = (d1a1k)/r, d4 = d2a2k/r, α1 = α/a1, β1 = (a1β)/r2, h1 − σ1 = (a1(h − σ))/r2, u1 = u/r, and g1 = (a1g)/r.

By simple computation, disease-free equilibrium M*(S*, 0, P*, Y*) can be obtained as follows.

P* = (1 − u1 − S*)(1 + b3S*), Y* = ((d3 − b3f1)S* − f1)/(1 + b3S*), and S* satisfies the following equation:
()
Conditions for existence of unique positive real root of (21) are as follows:
()

Remark 6. The above inequalities associated with taxation and vaccination control in (22) also guarantee existence and uniqueness of disease-free equilibrium M*.

Theorem 7. If the following inequalities hold

()
then model system (20) is locally stable around disease-free equilibrium M*.

Proof. For disease-free equilibrium M*(S*, 0, P*, Y*), the variational matrix of model system (20) around M* takes the following form:

()
where
()

It follows from V(S*, 0, P*, Y*) that the characteristic equation around M* is as follows:

()
where
()

It follows from Routh-Hurwitz criteria [13] that there are four eigenvalues with negative real part provided that , and , which derives that

()

In the following part, global stability analysis of model system (20) around disease-free equilibrium M* is investigated. Firstly, some preliminaries are discussed as follows.

Lemma 8 (see [31].)The unique interior equilibrium is globally stable in the domain G if it is locally stable and all trajectories in G converge to the unique interior equilibrium, where domain G satisfies the following conditions:

  • (i)

    the domain G is simply connected;

  • (ii)

    there is a compact absorbing set J ⊂ G.

Let V|2| be the second additive compound matrix [31, 32]. In the case of n = 4, V|2| can be written based on variational matrix of model system (20) around M*, which is as follows:
()
where Vij,  i, j = 1,2, 3,4, can be found in Theorem 7. Since V14 = 0, V21 = 0, V23 = 0, V24 = 0, V41 = 0, and V42 = 0, V|2| can be deduced as follows:
()
Furthermore, we have
()
where F(Z(T)) and Z(T) are defined based on model system (20), and the model system (20) can be interpreted as the matrix form
()
where Z(T) = (S(T), I(T), P(T), Y(T)) T and F(Z(T)) is given as follows:
()
By simple computation, it can be obtained that
()
Let
()
where
()
Consider the Lozinskii measure Γ of D with respect to a vector norm |·| in ℝ4 (see, [32]) and I (identity matrix), then it can be obtained that
()
Hence, it follows from simple computation that
()
where fi = Γ1(Dii)+|Dij| for i, j = 1,2, 3, and i ≠ j. |D12|, |D13|, |D21|, |D23|, |D31|, and |D32| are matrix norms with respect to the L1 vector norm, and Γ1 is the Lozinskii measure with respect to this vector norm.
Furthermore, let Δ = β1(h1 − σ1)/[β1 + (1 − S)(S(d3 − b3f1) − f1)] 2, then it can be computed that
()
According to Theorem 3 and definition of fi,   i = 1,2, 3, it follows that
()

Lemma 9. For element P(T) of the disease-free equilibrium M*, some inequalities about lim inf T→∞P(T) hold as follows:

  • (a)

    if a3d3 + c1(a3d3 − d4) ≤ 0, then

    ()

  • (b)

    if a3d3 + c1(a3d3 − d4) > 0, then

    • (i)

        −  , provided that a3d3(1 − u1 + m2 − m3) ≥ c1m3(a3d3 − d4),

    • (ii)

      , provided that a3d3(1 − u1 + m2 − m3) < c1m3(a3d3 − d4),

where m2 = max {e1, f1 + r(h1 − σ1)/g1} and m3 = k(e1 + 1) 2/4e1.

Proof. Based on Theorem 4 and nondimensionalized scaling of model system (20) mentioned in Section 4, it derives that

()

According to model system (20), let W(T) = d3S(T)+(d4/a3)I(T) + P(T). By calculating the time derivative of W(T) along the solutions of model system (20), it can be obtained that

()
where m2 = max {e1, f1 + r(h1 − σ1)/g1}.

If a3d3 + c1(a3d3 − d4) ≤ 0, then

()

According to W = d3S + (d4/a3)I + P, it follows from the standard comparison principle that

()

On the other hand, if a3d3 + c1(a3d3 − d4) > 0, then

()
where m3 = k(e1 + 1) 2/4e1.

According to W = d3S + (d4/a3)I + P, it follows from the standard comparison principle that

()
provided that a3d3(1 − u1 + m2 − m3) ≥ c1m3(a3d3 − d4).

Furthermore,

()
provided that a3d3(1 − u1 + m2 − m3) < c1m3(a3d3 − d4).

Let
()

Theorem 10. If the model system is locally stable around M* and inequality (22) holds, then

  • (a)

    if a3d3 + c1(a3d3 − d4) ≤ 0 and α1g1n1(h1 − σ1)/(β1g1 + rn1(h1 − σ1)) > l1 + l2 + l3, then model system (20) is globally stable around M*;

  • (b)

    if a3d3 + c1(a3d3 − d4) > 0, then

    • (i)

      model system (20) is globally stable around M* provided that  a3d3(1 − u1 + m2 − m3) ≥ c1m3(a3d3 − d4),  α1g1n2(h1 − σ1)/(β1g1 + rn2(h1 − σ1)) > l1  +  l2 + l3,

    • (ii)

      model system (20) is globally stable around M* provided that  a3d3(1 − u1 + m2 − m3) < c1m3(a3d3 − d4),  α1g1n3(h1 − σ1)/(β1g1 + rn3(h1 − σ1)) > l1  +  l2 + l3,

where ni,   i = 1,2, 3, and mi,   i = 2,3, have been defined in Lemma 9. li,   i = 1,2, 3, have been defined in (49)–(9).

Proof. According to model system (20), if inequality (22) holds, then there exists a unique disease-free equilibrium M*.

If a3d3 + c1(a3d3 − d4) ≤ 0 and α1g1n1(h1 − σ1)/(β1g1 + rn1(h1 − σ1)) > l1 + l2 + l3, then

()
which derives that
()

Based on robust Bendixson criterion [31, 32], inequality (51) ensures that there are no orbits (i.e., homoclinic orbits, heteroclinic cycles, and periodic orbits), which give rise to a simple closed rectifiable curve in ℝ4, invariant for the model system (20). Based on the above analysis, if model system (20) is locally stable around M*, then it follows from Lemma 8 that model system (20) is globally stable around M*.

If a3d3 + c1(a3d3 − d4) > 0, a3d3(1 − u1 + m2 − m3) ≥ c1m3(a3d3 − d4), and α1g1n2(h1 − σ1)/(β1g1 + rn2(h1 − σ1)) > l1 + l2 + l3, then

()
which derives that
()

Based on robust Bendixson criterion [31, 32], inequality (53) ensures that there are no orbits (i.e., homoclinic orbits, heteroclinic cycles, and periodic orbits), which give rise to a simple closed rectifiable curve in ℝ4, invariant for the model system (20). Based on the above analysis, if model system (20) is locally stable around M*, then it follows from Lemma 8 that model system (20) is globally stable around M*.

If a3d3 + c1(a3d3 − d4) > 0, a3d3(1 − u1 + m2 − m3) < c1m3(a3d3 − d4), and α1g1n3(h1 − σ1)/(β1g1 + rn3(h1 − σ1)) > l1 + l2 + l3, then

()
It derives that
()

Based on robust Bendixson criterion [31, 32], inequality (55) ensures that there are no orbits (i.e., homoclinic orbits, heteroclinic cycles, and periodic orbits), which give rise to a simple closed rectifiable curve in ℝ4, invariant for the model system (20). Based on the above analysis, if model system (20) is locally stable around M*, then it follows from Lemma 8 that model system (20) is globally stable around M*.

5. Optimal Control of Model System

With the purpose of regulating harvesting and protecting population from infectious disease within harvested eco-epidemiological system, we design an optimal control to maximize total discounted net revenue to society by using taxation and vaccination as control instruments. The path traced out by (S, I, P, Y) with optimal taxation σ1 and optimal vaccination u1 is also investigated.

Total discounted net economic revenue to society π(S, I, P, Y, σ1, u1, T)  = discounted economic revenue of harvesting + discounted economic revenue to regulatory agency − vaccination cost.

It follows from model system (20), that the following can be obtained:
()
where δ is the instantaneous annual rate of discount and the optimization problem is subject to the model system (20). B is a positive weight parameter associated with the square of control variable to balance size of the terms; see [20, 21, 24, 25] and references therein. represents vaccination cost of susceptible prey population.

Remark 11. Vaccination cost discussed in this section is a quadratic cost, which is the simplest and widest used nonlinear representation of vaccination cost; see [20, 21, 24, 25] and references therein. Actually, when nonlinear description is adopted, it may be not completely clear which nonlinear form must be appropriately chosen. In this case, choosing the simplest form compatible with mathematical requirements (existence, well-posedness of maximization problems, etc.) is a possible guideline; see [20, 21, 24] and references therein. Based on the above introduction, we consider a quadratic cost on the optimal control problem in this section. It should be noted that other nonlinear functions might provide a better description of the actual vaccination cost due to the increase of vaccination cost when most of population is already removed (vaccinated or immune); see [21, 24] and references therein.

5.1. Design of Optimal Control

Our objective is to maximize the following optimization problem:
()
By using the Pontryagin’s maximum principle [12], the associated Hamiltonian function is constructed by
()
where λi(T),   i = 1,2, 3,4, are adjoint variables. σ1 and u1 are the control variables. According to [33], the conditions for a singular control to be optimal can be obtained by  ∂R/∂σ1 = 0 and ∂R/∂u1 = 0, from which we get
()
According to Theorem 3, it follows that
()
For adjoint variables λi(T),   i = 1,2, 3,4, we have
()
By substituting λ4(T) = 0 into the Equation dλ4(T)/dT = −∂R/∂Y, it follows that
()
By virtue of (62), it gives that
()
By associating with M*(S*, 0, P*, Y*), the above equation can be deduced as follows:
()
where Q1 = h1β1/(β1 + P*Y*) 2 − g1/P* and Q2 = [2b3S* − b3 + 1 + b3u1]S*/(1 + b3S*).
By solving (64), it can be obtained that
()
By virtue of (62), it gives that
()
By associating with M*(S*, 0, P*, Y*), the above equation can be deduced as follows:
()
where Q3 = [(b4 + b3 + b3c1)S* − b4 + c1 + 1 + b4u1]S*/(1 + b3S*) and Q5 = [a3 + e1 − (c1 + a3)S*].
According to (65), (67) can be rewritten as follows:
()
where Q4 = d3Q3/(δ + Q2)(1 + b3S*) − [d4 + (b3d4 − b4d3)S*].
By solving (68), it can be obtained that
()
Based on (65) and (69), it can be obtained that
()
By associating with M*(S*, 0, P*, Y*), (70) can be deduced as follows:
()
By solving the above equation, it can be obtained that
()
In order to obtain an optimal equilibrium solution, it can be obtained by considering the disease-free equilibrium M* and substituting (72) into (62), and it derives that
()
Equation (73) provides an equation to the singular path and gives the optimal equilibrium levels of population S* = Sδ,  P* = (1 − u1 − Sδ)(1 + b3Sδ), Y* = ((d3 − b3f1)Sδ − f1)/(1 + b3Sδ). Then, the optimal equilibrium levels of taxation and vaccination control can be obtained as follows:
()

Remark 12 (according to [13]). λi(T)eδT  (i = 1,2, 3,4) represent unusual shadow prices along the singular path. From (65), (69), and (72), it may be concluded that these shadow prices remain constant over time interval in an optimum equilibrium when they strictly satisfy the transversality condition at ∞ [34]. Furthermore, they remain bounded as T → ∞.

Generally, there is a strong ecological relationship between predator population and susceptible prey population in the harvested eco-epidemiological system, and these two species are usually influenced by each other in several aspects. The imposition of taxation and vaccination defined in (74) act as a deterrent to regulate harvest effort on predator population and control the spread of infectious disease within eco-epidemiological prey predator system, which can not only guarantee the sustainable development of predator population, but also benefit the ecological balance in the ecosystem and sustainable development of other relevant species in the harvested eco-epidemiological system.

5.2. Numerical Simulation

With the help of MATLAB, simulation work with hypothetical set of parameters is performed to understand the theoretical results which have been established in Section 5.1 of this paper. The values of parameters are cited from [9, 12], which are given as follows: r = 1,  k = 1,  a1 = 1,  b1 = 2.34,  b2 = 3,  c = 0.01,  a2 = 0.344,  e = 0.051,  d1 = 0.21,  d2 = 0.6774,  f = 0.001,  α = 0.4,  h = 1.67,  β = 1.1,  g = 0.41,  δ = 0.05,  and   B = 1.

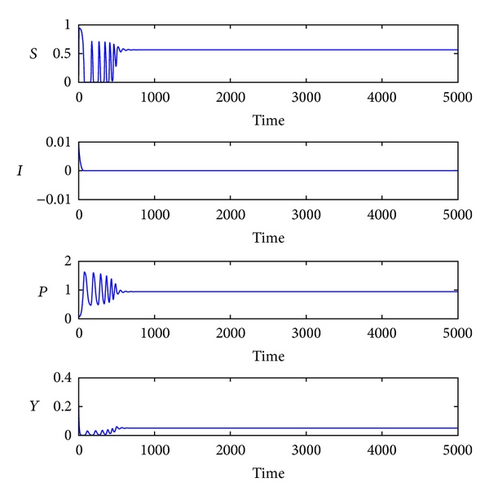
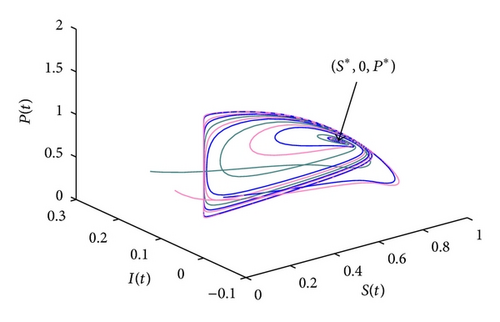
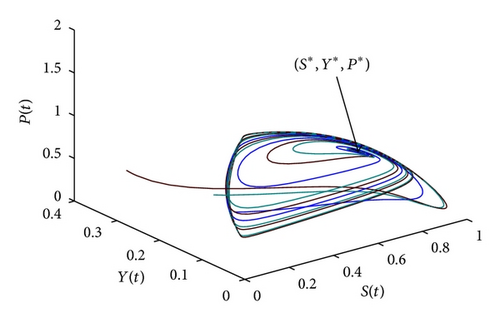
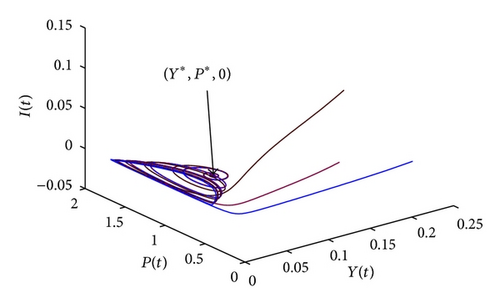
According to the parameters given above, it follows from (22) that the range of the taxation σ1 ∈ [0.4496,1.6336] and vaccination u1 ∈ [−1.3663,1), which guarantees that there exists a unique disease-free equilibrium. Based on (74), it can be computed that the optimal taxation and optimal vaccination control is σδ = 1.0653 and u1δ = 0.483, respectively. Since σδ ∈ [0.4496,1.6336] and u1δ ∈ [−1.3663,1), it can be obtained that there exists a unique disease-free equilibrium M* corresponding to the optimal taxation and vaccination control, that is, M*(0.5648,0, 0.9406,0.0501). According to Theorem 10, model system (20) is globally stable around M*, whose dynamical responses can be shown in Figure 1, and the corresponding phase portraits are shown in Figure 2 (S-I-P space), Figure 3 (S-Y-P space), and Figure 4 (Y-P-I space) with different initial values.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Dynamical responses of model system (20) with the optimal taxation and vaccination σδ = 1.0653 and u1δ = 0.483.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Phase portrait (S-I-P space) of model system (20) with σδ = 1.0653, and u1δ = 0.483 and differential initial values, which indicates model system (20) is globally stable around M*(0.5648,0, 0.9406,0.0501).
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Phase portrait (S-Y-P space) of model system (20) with σδ = 1.0653 and u1δ = 0.483 and differential initial values, which indicates model system (20) is globally stable around M*(0.5648,0, 0.9406,0.0501).
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Phase portrait (Y-P-I space) of model system (20) with σδ = 1.0653 and u1δ = 0.483 and differential initial values, which indicates model system (20) is globally stable around M*(0.5648,0, 0.9406,0.0501).

6. Conclusion

It is well known that studies on ecology and epidemiology share some common features. Nowadays, taxation is extensively used as economic control instrument to protect the population of the prey predator system from overexploitation, and vaccination is widely adopted to control spread of infectious disease within harvested eco-epidemiological system. Based on superiority of taxation control in regulating harvesting and effectiveness of vaccination in protecting population from infectious disease, it motives the introduction of taxation and vaccination control into model proposed in this paper. In this paper, a harvested eco-epidemiological model is established to investigate the dynamics effects of vaccination and taxation control on the population dynamics. We extend the work in [9] by incorporating the harvest effort into eco-epidemiological prey predator system. Vaccination and taxation are chosen as controlling instruments to protect population from infectious disease and regulate harvesting on predator, respectively.

Since it is of more biological significance to consider the effect of interacting species when it comes to discussing dynamics of epidemiological model, conditions that influence nonnegativeness and boundedness of solutions are discussed, which can be found in Theorems 3 and 4. Local stability analysis around disease-free equilibrium is studied in Theorem 7. Based on robust Bendixson criterion, global stability of model system around the unique disease-free equilibrium is discussed in Theorem 10, which is theoretically beneficial to studying the coexistence and interaction mechanism of harvested eco-epidemiological prey predator system. By using Pontryagin’s maximum principle, optimal vaccination and taxation control are derived to ensure the sustainable development of biological resource and protect population from infectious disease in the fifth section of this paper. It reveals that the total user’s cost of harvest per unit effort must be equal to the discounted value of the future price at the steady-state level, and infectious disease among prey population can be removed with optimal vaccination strategy on susceptible prey population.

It should be noted that the optimal control is obtained based on an interesting reflection, which discusses the impact and efficiency of optimal control and deducts a tendency for the management of biological resource. Since infectious disease spreads within the eco-epidemiological prey predator system and the commercial harvesting exists extensively in the natural world, it is necessary to discuss optimal strategy associated with net harvesting revenue and vaccination cost. Hence, theoretical analysis obtained in the fifth section is constructive for regulatory agency to formulate constructive policies and maintain the sustainable harvesting and effective vaccination by means of optimal taxation and vaccination control; it makes the work studied in this paper have some new and positive features.

Acknowledgments

The authors are thankful to the learned reviewer and editors for his/her useful suggestions and comments. This work is supported by National Natural Science Foundation of China, Grant no. 61104003, Grant no. 61273008, and Grant no. 61104093, Research Foundation for Doctoral Program of Higher Education of Education Ministry, Grant no. 20110042120016, Hebei Province Natural Science Foundation, Grant no. F2011501023, Fundamental Research Funds for the Central Universities, Grant no. N120423009, and Research Foundation for Science and Technology Pillar Program of Northeastern University at Qinhuangdao, Grant no. XNK201301. This work is supported by State Key Laboratory of Integrated Automation of Process Industry, Northeastern University, supported by Hong Kong Admission Scheme for Mainland Talents and Professionals, Hong Kong Special Administrative Region.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.