Abstract and Applied Analysis
Volume 2013, Issue 1 936952
Research Article
Open Access

Stability in a Simple Food Chain System with Michaelis-Menten Functional Response and Nonlocal Delays

Wenzhen Gan, 

Wenzhen Gan

School of Mathematics and Physics, Jiangsu Teachers University of Technology, Changzhou 213001, China jstu.edu.cn

Search for more papers by this author
Canrong Tian, 

Canrong Tian

Basic Department, Yancheng Institute of Technology, Yangcheng 224003, China ycit.edu.cn

Search for more papers by this author
Qunying Zhang, 

Qunying Zhang

School of Mathematical Science, Yangzhou University, Yangzhou 225002, China yzu.edu.cn

Search for more papers by this author
Zhigui Lin, 

Corresponding Author

Zhigui Lin

School of Mathematical Science, Yangzhou University, Yangzhou 225002, China yzu.edu.cn

Search for more papers by this author
First published: 05 September 2013
https://doi.org/10.1155/2013/936952
Citations: 1
Academic Editor: Rodrigo Lopez Pouso

Abstract

This paper is concerned with the asymptotical behavior of solutions to the reaction-diffusion system under homogeneous Neumann boundary condition. By taking food ingestion and species′ moving into account, the model is further coupled with Michaelis-Menten type functional response and nonlocal delay. Sufficient conditions are derived for the global stability of the positive steady state and the semitrivial steady state of the proposed problem by using the Lyapunov functional. Our results show that intraspecific competition benefits the coexistence of prey and predator. Furthermore, the introduction of Michaelis-Menten type functional response positively affects the coexistence of prey and predator, and the nonlocal delay is harmless for stabilities of all nonnegative steady states of the system. Numerical simulations are carried out to illustrate the main results.

1. Introduction

The overall behavior of ecological systems continues to be of great interest to both applied mathematicians and ecologists. Two species predator-prey models have been extensively investigated in the literature. But recently more and more attention has been focused on systems with three or more trophic levels. For example, the predator-prey system for three species with Michaelis-Menten type functional response was studied by many authors [1–4]. However, the systems in [1–4] are either with discrete delay or without delay or without diffusion. In view of individuals taking time to move, spatial dispersal was dealt with by introducing diffusion term to corresponding delayed ODE model in previous literatures, namely, adding a Laplacian term to the ODE model. In recent years, it has been recognized that there are modelling difficulties with this approach. The difficulty is that diffusion and time delay are independent of each other, since individuals have not been at the same point at previous times. Britton [5] made a first comprehensive attempt to address this difficulty by introducing a nonlocal delay; that is, the delay term involves a weighted-temporal average over the whole of the infinite domain and the whole of the previous times.

There are many results for reaction-diffusion equations with nonlocal delays [5–18]. The existence and stability of traveling wave fronts were studied in reaction-diffusion equations with nonlocal delay [5–9]. The stability of impulsive cellular neural networks with time varying was discussed in [10] by means of new Poincare integral inequality. The asymptotic behavior of solutions of the reaction-diffusion equations with nonlocal delay was investigated in [11, 12] by using an iterative technique and in [13–15] by the Lyapunov functional. The stability and Hopf bifurcation were discussed in [16] for a diffusive logistic population model with nonlocal delay effect.

Motivated by the work above, we are concerned with the following food chain model with Michaelis-Menten type functional response:
()
for t > 0, x ∈ Ω with homogeneous Neumann boundary conditions
()
and initial conditions
()
where ϕi is bounded, Hölder continuous function and satisfies ∂ϕi/∂ν = 0 (i = 1,  2,  3) on (−∞, 0] × ∂Ω. Here, Ω is a bounded domain in ℝn with smooth boundary ∂Ω and ∂/∂ν is the outward normal derivative on ∂Ω. ui(t, x) represents the density of the ith species (prey, predator, and top predator resp.) at time t and location x and thus only nonnegative ui(t, x) is of interest. The parameter a1 is the intrinsic growth rate of the prey, and a2 and a3 are the death rates of the predator and top-predator. aii is the intraspecific competitive rate of the ith species. a12 is the maximum predation rate. a23 and a32 are the efficiencies of food utilization of the predator and top predator, respectively. We assume the predator and top predator show the Michaelis-Menten (or Holling type II) functional response with u1/(m1 + u1) and u2/(m2 + u2), respectively, where m1 and m2 are half-saturation constants. For a through biological background of similar models, see [18, 19]. As our most knowledge, the tritrophic food chain model has been found to have many interesting biological properties, such as the coexistence and the Hopf bifurcation. However, the effect of nonlocal time delays on the coexistence has not been reported. Our paper mainly concerns this perspective.

Additionally, (i = 1,  2) represents the nonlocal delay due to the ingestion of predator; that is, mature adult predator can only contribute to the production of predator biomass. The boundary condition in (2) implies that there is no migration across the boundary of Ω.

The main purpose of this paper is to study the global asymptotic behavior of the solution of system (1)–(3). The preliminary results are presented in Section 2. Section 3 contains sufficient conditions for the global asymptotic behaviors of the equilibria of system (1)–(3) by means of the Lyapunov functional. Numerical simulations are carried out to show the feasibility of the conditions in Theorems 8–10 in Section 4. Finally, a brief discussion is given to conclude this work.

2. Preliminary Results

In this section, we present several preliminary results that will be employed in the sequel.

Lemma 1 (see [3].)Let a and b be positive constants. Assume that ϕ,   φ ∈ C1(a, +∞),   φ(t) ≥ 0, and ϕ is bounded from below. If ϕ′(t)≤−bφ(t) and φ′(t) ≤ K in [a, +∞) for some positive constant K, then lim t→+∞φ(t) = 0.

The following lemma is the Positivity Lemma in [20].

Lemma 2. Let and satisfy

()
where . If bij ≥ 0 for j ≠ i and cij ≥ 0 for all i, j = 1,2, 3. Then ui(t, x) ≥ 0 on . Moreover, if the initial function is nontrivial, then ui > 0 in .

Lemma 3 (see [20].)Let and be a pair of constant vector satisfying and let the reaction functions satisfy local Lipschitz condition with . Then system (1)–(3) admits a unique global solution u(t, x) such that

()
whenever , (t, x)∈(−∞, 0] × Ω.

The following result was obtained by the method of upper and lower solutions and the associated iterations in [21].

Lemma 4 (see [21].)Let be the nontrivial positive solution of the system

()
where A1 ≥ 0,   B, A2, τ > 0. The following results hold:
  • (1)

    if B ± A1 > 0, then u → (B ± A1)/A2 uniformly on as t → ∞;

  • (2)

    if B ± A1 ≤ 0, then u → 0 uniformly on as t → ∞.

Throughout this paper, we assume that
()
where Gi(x, y, t) is a nonnegative function, which is continuous in for each t ∈ [0, +∞) and measurable in t ∈ [0, +∞) for each pair .

Now we prove the following propositions which will be used in the sequel.

Proposition 5. For any nonnegative initial function, the corresponding solution of system (1)–(3) is nonnegative.

Proof. Suppose that (u1, u2, u3) is a solution and satisfies with T ≤ +∞. Choose 0 < τ < T. Then

()
where
()
It follows from Lemma 2 that . Due to the arbitrariness of τ, we have ui ≥ 0 for .

Proposition 6. System (1)–(3) with initial functions ϕi admits a unique global solution (u1, u2, u3) satisfying 0 ≤ ui(t, x) ≤ Mi for i = 1,2, 3, where Mi is defined as

()

Proof. It follows from standard PDE theory that there exists a T > 0 such that problem (1)–(3) admits a unique solution in . From Lemma 2 we know that ui(t, x) ≥ 0 for . Considering the first equation in (1), we have

()
Using the maximum principle gives that u1 ≤ M1. In a similar way, we have ui ≤ Mi for i = 2,3. It is easy to see that (0,0, 0) and (M1, M2, M3) are a pair of coupled upper and lower solutions to system (1)–(3) from the direct computation. In virtue of Lemma 3, system (1)–(3) admits a unique global solution (u1, u2, u3) satisfying 0 ≤ ui(t, x) ≤ Mi for i = 1,2, 3. In addition, if ϕ1(t, x), ϕ2(t, x), ϕ3(x), (t, x)∈(−∞, 0] × Ω is nontrivial, it follows from the strong maximum principle that ui(t, x) > 0  (i = 1,2, 3) for all .

3. Global Stability

In this section, we study the asymptotic behavior of the equilibrium of system (1)–(3). In the beginning, we show the existence and uniqueness of positive steady state.

Let us consider the following equations:
()
A direct computation shows that the above equations have only one positive solution if and only if
()
is satisfied. Taking H1 into account, we consider the equation , which corresponds to L3 in Figure 1.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Graphs of the equations in (12). L3 is the boundary condition (a3 = a32v2/(m2 + v2)) and L2 corresponds to −a2 + a21(v1/(m1 + v1  )) − a22v2 = 0, while L1 corresponds to a1 − a11v1 − a12v2/(m1 + v1  ) = 0. Intersection point between L1 and L2 gives the positive solution to (12). Parameter values are listed in the example in Section 4.
It is clear that if , the intersection point always lies in L3. Let
()
Suppose that H1 and H2 hold. We take u3 as a parameter and consider the following system:
()
When the parameter u3 is sufficiently small, the first two equations in (15) can be approximated by (12). Moreover, by continuously increasing the value of u3,  L3 goes up, and meanwhile the intersection point between L1 and L2 also goes up. However, L3 goes up faster than L2, while L1 keeps still. In other words, there exists a critical value u3 such that the intersection point lies in L3, which implies that there is a unique positive solution to (15), or equivalently (1)–(3).

Lemma 7. Assume that H2 and G2 hold, and then the positive steady state E* of system (1)–(3) is locally asymptotically stable.

Proof. We get the local stability of E* by performing a linearization and analyzing the corresponding characteristic equation. Similarly as in [22], let 0 < μ1 < μ2 < μ3 < … be the eigenvalues of −Δ on Ω with the homogeneous Neumann boundary condition. Let E(μi) be the eigenspace corresponding to μi in , for i = 1,2, 3, … . Let

()
{φij, j = 1, …, dim E(μi)} be an orthonormal basis of E(μi), and Xij = {c · φij∣c ∈ R3}. Then
()
Let D = diag (D1, D2, D3) and . Then the linearization of (1) is vt = Lv = DΔv + Fv(E*)v,   Fv(E*)v = {cij}, where . The coefficients bij are defined as follows:
()
Since Xi is invariant under the operator L for each i ≥ 1, then the operator L on Xi is vt = Lv = Dμiv + Fv(E*)v. Let vi = cieλt(i = 1,2, 3) and we can get the characteristic equation φi(λ) = λ3 + Aiλ2 + Biλ + Ci = 0, where Ai, Bi, and Ci are defined as follows:
()
It is easy to see that b12,   b23,   b33 < 0 and b21,   b32 > 0. It follows from assumption G1 and G2 that a11 < 0,   a22 < 0. So Ai > 0,   Bi > 0,   Ci > 0 and AiBi − Ci > 0 for i ≥ 1 from the direct calculation. According to the Routh-Hurwitz criterion, the three roots λi,1,   λi,2,   λi,3 of φi(λ) = 0 all have negative real parts.

By continuity of the roots with respect to μi and Routh-Hurwitz criterion, we can conclude that there exists a positive constant ε such that

()
Consequently, the spectrum of L, consisting only of eigenvalues, lies in {Reλ ≤ −ε}. It is easy to see that E* is locally asymptotically stable and follows from Theorem 5.1.1 of [23].

Theorem 8. Assume that

()
H2 and G2 hold, and the positive steady state E* of system (1)–(3) with nontrivial initial function is globally asymptotically stable.

Proof. It is easy to see that the equations in (1) can be rewritten as

()
Define
()
where α and β are positive constants to be determined. Calculating the derivatives V(t) along the positive solution to the system (1)–(3) yields
()
where
()
Applying the inequality ab ≤ ϵa2 + (1/4ϵ)b2, we derive from (25) that
()
According to the property of the Kernel functions Ki(x, y, t), (i = 1,2), we know that
()
Define a new Lyapunov functional as follows:
()
It is derived from (27) and (28) that
()
Since (u1, u2, u3) is the unique positive solution of system (1). Using Proposition 5, there exists a constant C which does not depend on or t ≥ 0 such that (i = 1,2, 3) for t ≥ 0. By Theorem A2 in [24], we have
()
Assume that
()
and denote
()
Then (29) is transformed into
()
If we choose
()
then li > 0  (i = 1,2, 3). Therefore, we have
()

From Proposition 6 we can see that the solution of system (1) and (3) is bounded, and so are the derivatives of (i = 1,  2,  3) by the equations in (1). Applying Lemma 1, we obtain that

()
Recomputing E′(t) gives
()
where /. Using (30) and (1), we obtain that the derivative of g(t) is bounded in [1, +∞). From Lemma 1, we conclude that g(t) → 0 as t → ∞. Therefore
()
Applying the Poincaré inequality
()
leads to
()
where and λ is the smallest positive eigenvalue of −Δ with the homogeneous Neumann condition. Therefore,
()
So we have as t → ∞. Similarly, and as t → ∞. According to (30), there exists a subsequence tm, and non-negative functions , such that
()
Applying (40) and noting that , we then have , (i = 1,2, 3). That is,
()

Furthermore, the local stability of E* combining with (43) gives the following global stability.

Theorem 9. Assume that

()
H4 and G4 hold, and then the semi-trivial steady state E2 of system (1)–(3) with non-trivial initial functions is globally asymptotically stable.

Proof. It is obvious that system (1)–(3) always has two non-negative equilibria (u1, u2, u3) as follows: E0 = (0, 0, 0) and E1 = (a1/a11, 0, 0). If H1 and H4 are satisfied, system (1) has the other semitrivial solution denoted by , where

()

We consider the stability of E2 under condition H1 and H4. Equation (1) can be rewritten as

()
Similar to the argument of Theorem 8, we have and as t → ∞ uniformly on provided that the following additional condition holds:
()
Next, we consider the asymptotic behavior of u3(t, x). Let
()
Then there exists t1 > 0 such that
()
Consider the following two systems:
()
Combining comparison principle with (50), we obtain that
()
By Lemma 4, we obtain
()
which implies that lim t→∞u3(t, x) = 0 uniformly on .

Theorem 10. Suppose that G5 and G6 hold, and then the semi-trivial steady state E1 of system (1)–(3) with non-trivial initial functions is globally asymptotically stable.

Proof. We study the stability of the semi-trivial solution . Similarly, the equations in (1) can be written as

()
Define
()
Calculating the derivative of V(t) along E1, we get from (54) that
()
Define
()
It is easy to see that
()
Assume that
()
Let
()
Choose
()
Then we get li > 0 (i = 1,  2,  3). Therefore we have
()
uniformly on .

Next, we consider the asymptotic behavior of u2(t, x) and u3(t, x). For any T > 0, integrating (57) over [0, T] yields
()
where . It implies that for the constant Ci which is independent of T. Now we consider the boundedness of and . From the Green′s identity, we obtain
()
Note that
()
Thus, we get . In a similar way, we have . Here C4 and C5 are independent of T.
It is easy to see that u2(t, x), u3(t, x) ∈ L2((0, ∞); W1,2(Ω)). These imply that
()
From the Sobolev compact embedding theorem, we know
()
In the end, we show that the trivial solution E0 is an unstable equilibrium. Similarly to the local stability to E*, we can get the characteristic equation of E0 as
()
If i = 1, then μ1 = 0. It is easy to see that this equation admits a positive solution λ = a1. According to Theorem 5.1 in [23], we have the following result.

Theorem 11. The trivial equilibrium E0 is an unstable equilibrium of system (1)–(3).

4. Numerical Illustrations

In this section, we perform numerical simulations to illustrate the theoretical results given in Section 3.

In the following, we always take Ω = [0, π],   Ki(x, y, t) = Gi(x, y, t)ki(t), where (i = 1,2) and
()
However, it is difficult for us to simulate our results directly because of the nonlocal term. Similar to [25], the equations in (1) can be rewritten as follows:
()
where
()
Each component is considered with homogeneous Neumann boundary conditions, and the initial condition of vi is
()
In the following examples, we fix some coefficients and assume that d1 = d2 = d3 = 1,   a1 = 3,   a12 = 1,   m1 = m2 = 1,   a2 = 1,   a22 = 12,   a23 = 1,   a33 = 12, and τ* = 1. The asymptotic behaviors of system (1)–(3) are shown by choosing different coefficients a11,   a21,   a3, and a32.

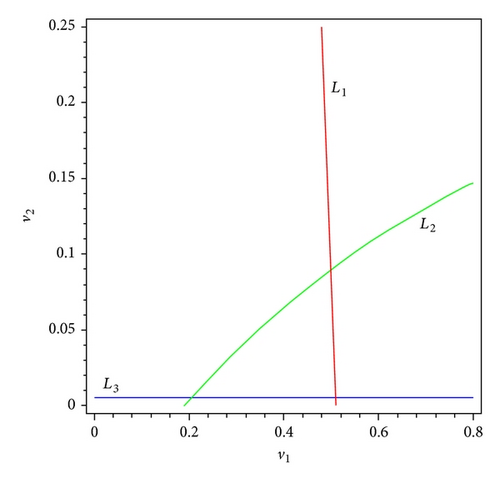
Example 12. Let a11 = 53/9,   a21 = 81/13,   a3 = 1/13 and a32 = 14. Then it is easy to see that the system admits a unique positive equilibrium E*(1/2,1/12,1/12). By Theorem 8, we see that the positive solution (u1(t, x), u2(t, x), u3(t, x)) of system (1)–(3) converges to E* as t → ∞. See Figure 2.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
Global stability of the positive equilibrium E* with an initial condition (ϕ1, ϕ2, ϕ3) = (2.7 + 0.5sinx, 2.7 + 0.5cos x, 2.7 + 0.5sinx).
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
Global stability of the positive equilibrium E* with an initial condition (ϕ1, ϕ2, ϕ3) = (2.7 + 0.5sinx, 2.7 + 0.5cos x, 2.7 + 0.5sinx).
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
Global stability of the positive equilibrium E* with an initial condition (ϕ1, ϕ2, ϕ3) = (2.7 + 0.5sinx, 2.7 + 0.5cos x, 2.7 + 0.5sinx).

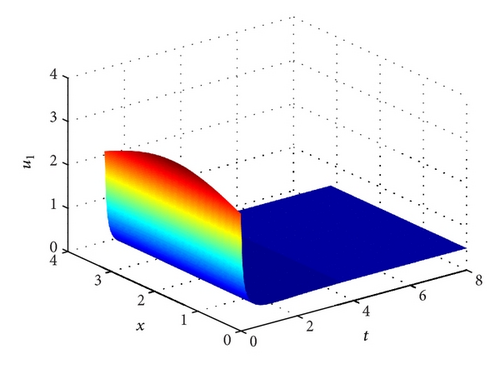
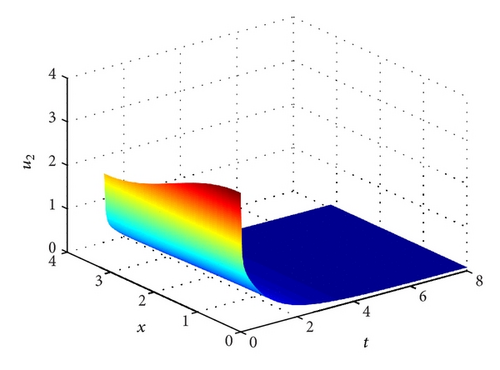
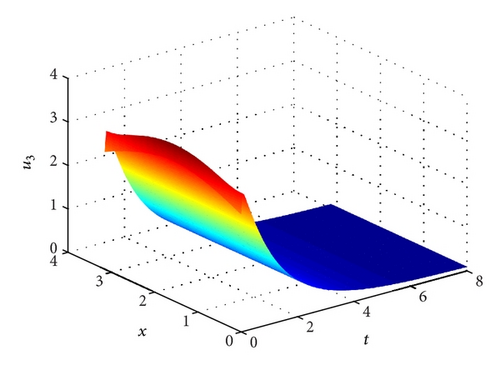
Example 13. Let a11 = 6,   a21 = 12,   a3 = 1/4 and a32 = 1. Clearly, H2 does not hold. Hence, the positive steady state is not feasible. System (1) admits two semi-trivial steady state E2(0.4732,0.2372,0) and E1(1/2,0, 0). According to Theorem 9, we know that the positive solution (u1(t, x),   u2(t, x),   u3(t, x)) of system (1)–(3) converges to E2 as t → ∞. See Figure 3.

Details are in the caption following the image
Figure 3 (a)
Open in figure viewerPowerPoint
Global stability of the positive equilibrium E2 with an initial condition (ϕ1, ϕ2, ϕ3) = (2.7 + 0.5sinx, 2.7 + 0.5cos x, 2.7 + 0.5sinx).
Details are in the caption following the image
Figure 3 (b)
Open in figure viewerPowerPoint
Global stability of the positive equilibrium E2 with an initial condition (ϕ1, ϕ2, ϕ3) = (2.7 + 0.5sinx, 2.7 + 0.5cos x, 2.7 + 0.5sinx).
Details are in the caption following the image
Figure 3 (c)
Open in figure viewerPowerPoint
Global stability of the positive equilibrium E2 with an initial condition (ϕ1, ϕ2, ϕ3) = (2.7 + 0.5sinx, 2.7 + 0.5cos x, 2.7 + 0.5sinx).

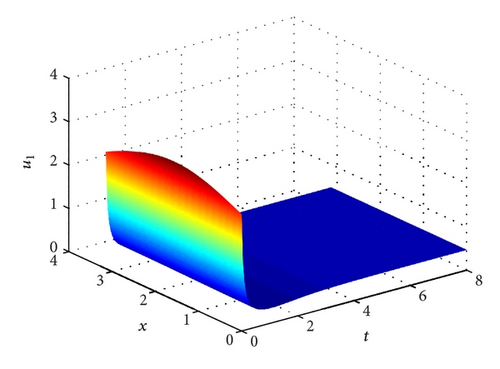
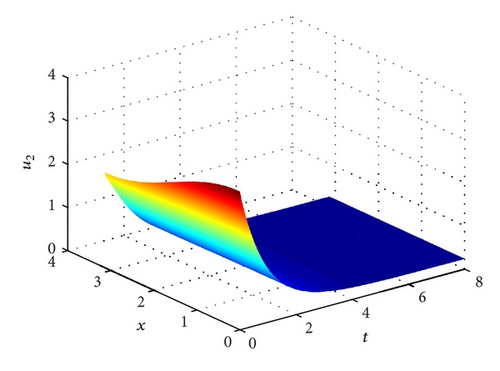
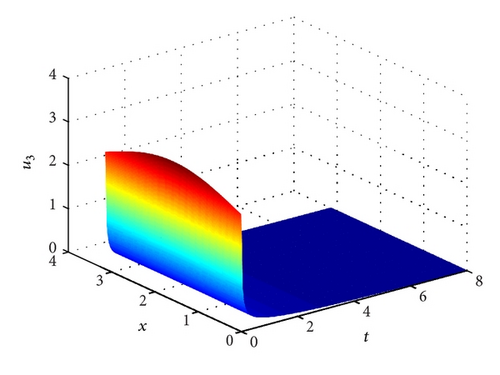
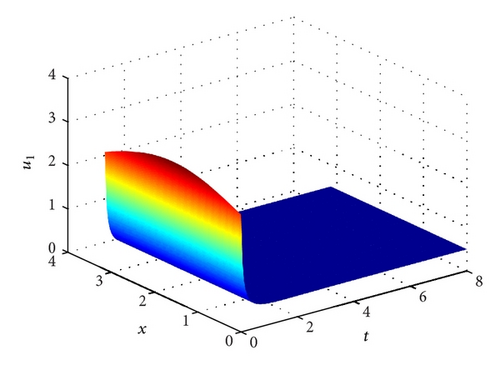
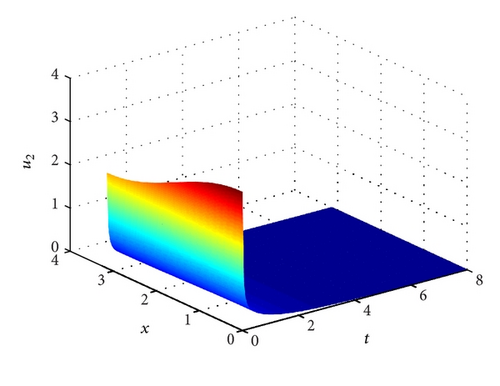
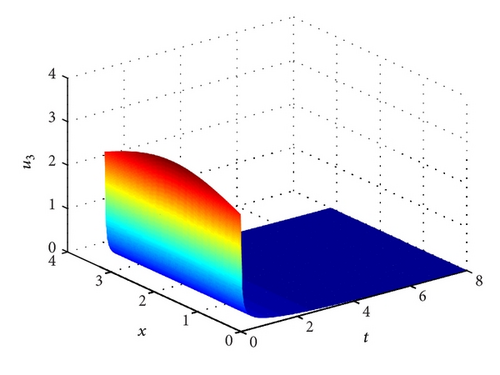
Example 14. Let a11 = 6,   a21 = 2,   a3 = 1/4 and a32 = 1. Clearly, H1 does not hold. Hence, E* and E2 are not feasible. System (1) has a unique semi-trivial steady state E1(1/2,0, 0). According to Theorem 10 we know that the positive solution (u1(t, x),   u2(t, x),   u3(t, x)) of system (1)–(3) converges to E1 as t → ∞. See Figure 4.

Details are in the caption following the image
Figure 4 (a)
Open in figure viewerPowerPoint
Global stability of the positive equilibrium E1 with an initial condition (ϕ1, ϕ2, ϕ3) = (2.7 + 0.5sinx, 2.7 + 0.5cos x, 2.7 + 0.5sinx).
Details are in the caption following the image
Figure 4 (b)
Open in figure viewerPowerPoint
Global stability of the positive equilibrium E1 with an initial condition (ϕ1, ϕ2, ϕ3) = (2.7 + 0.5sinx, 2.7 + 0.5cos x, 2.7 + 0.5sinx).
Details are in the caption following the image
Figure 4 (c)
Open in figure viewerPowerPoint
Global stability of the positive equilibrium E1 with an initial condition (ϕ1, ϕ2, ϕ3) = (2.7 + 0.5sinx, 2.7 + 0.5cos x, 2.7 + 0.5sinx).

5. Discussion

In this paper, we incorporate nonlocal delay into a three-species food chain model with Michaelis-Menten functional response to represent a delay due to the gestation of the predator. The conditions, under which the spatial homogeneous equilibria are asymptotically stable, are given by using the Lyapunov functional.

We now summarize the ecological meanings of our theoretical results. Firstly, the positive equilibrium E* of system (1)–(3) exists under the high birth rate of the prey (a1) and low death rates (a2 and a3) of predator and top predator. E* is globally stable if the intraspecific competition a11 is neither too big nor too small and the maximum harvest rates a12, a23 are small enough. Secondly, the semi-trivial equilibrium E2 of system (1)–(3) exists if the birth rate of the prey (a1) is high, death rate of predator a2 is low, and the death rate (a3) exceeds the conversion rate from predator to top predator (a32). E2 is globally stable if the maximum harvest rates a12, a23 are small and the intra-specific competition a11 is neither too big nor too small. Thirdly, system (1)–(3) has only one semi-trivial equilibrium E1 when the death rate (a2) exceeds the conversion rate from prey to predator (a21). E1 is globally stable if intra-specific competitions (a11, a22, and a33) are strong. Finally, E0 is unstable and the non-stability of trivial equilibrium tells us that not all of the populations go to extinction. Furthermore, our main results imply that the nonlocal delay is harmless for stabilities of all non-negative steady states of system (1)–(3).

There are still many interesting and challenging problems with respect to system (1)–(3), for example, the permanence and stability of periodic solution or almost periodic solution. These problems are clearly worthy for further investigations.

Acknowledgments

This work is partially supported by PRC Grants NSFC 11102076 and 11071209 and NSF of the Higher Education Institutions of Jiangsu Province (12KJD110002 and 12KJD110008).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.