A finite element method (FEM) for multiterm fractional partial differential equations (MT-FPDEs) is studied for obtaining a numerical solution effectively. The weak formulation for MT-FPDEs and the existence and uniqueness of the weak solutions are obtained by the well-known Lax-Milgram theorem. The Diethelm fractional backward difference method (DFBDM), based on quadrature for the time discretization, and FEM for the spatial discretization have been applied to MT-FPDEs. The stability and convergence for numerical methods are discussed. The numerical examples are given to match well with the main conclusions.

1. Introduction

In recent years, the numerical treatment and supporting analysis of fractional order differential equations has become an important research topic that offers great potential. The FEMs for fractional partial differential equations have been studied by many authors (see [1–3]). All of these papers only considered single-term fractional equations, where they only had one fractional differential operator. In this paper, we consider the MT-FPDEs, which include more than one fractional derivative. Some authors also considered solving linear problems with multiterm fractional derivatives (see [4, 5]). This motivates us to consider their effective numerical solutions for such MT-FPDEs, which have been proposed in [6, 7].

Let Ω = (0, X) ^d, where d ≥ 1 is the space dimension. We consider the MT-FPDEs with the Caputo time fractional derivatives as follows:

()

where the operator P(^CD_t)u(t, x) is defined as

()

with 0 < α_s < α_s−1 < ⋯<α₁ < α < 1 and

. Here

denotes the left Caputo fractional derivative with respect to the time variable t and Δ_x denotes the Laplace operator with respect to the space variable x.

Some numerical methods have been considered for solving the multiterm fractional differential equations. In [8], Liu et al. investigate some effective numerical methods for time fractional wave-diffusion and diffusion equations:

()

where k and L are arbitrary positive constants and f(t, x) is a sufficiently smooth function. The authors consider the implicit finite difference methods (FDMs) and prove that it is unconditionally stable. The error estimate of the FDM is O(Δt + Δt^2−α + Δx), where Δt and Δx are the time and space step size, respectively. They also investigate the fractional predictor-corrector methods (FPCMs) of the Adams-Moulton methods for multiterm time fractional differential equations (1) with order {α_i} _i=1,…,s by solving the equivalent Volterra integral equations. The error estimate of the FPCM is

. In recent years, there are some articles for the predictor-correction method for initial-value problems (see [9–14]). For the application of the FDMs, there have been many research articles as follows. In [15–20], Simos et al. investigate the numerical methods for solving the Schrödinger equation. In [21–24], the Runge-Kutta methods are considered and applied to get the numerical solution of orbital problems. For long-time integration, the Newton-Cotes formulae are considered in [25–27].

In [28], Badr investigate the FEM for linear multiterm fractional differential equations with one variable as follows:

()

where A_i(x) are known functions. The author gives the details of the modified Galerkin method for the above equations and makes the numerical example for checking the numerical method. In [29], Ford et al. consider the FEM for (5) with singular fractional order and obtain the error estimate O(Δt^2−α + Δx²). In this paper, we follow the work in [29] and consider the FEM for solving MT-FPDEs (1)–(3). Then, we prove the stability and convergence of the FEM for MT-FPDEs and make the error estimate.

The paper is organized as follows. In Section 2, the weak formulation of the MT-FPDEs is given and the existence and uniqueness results for such problems are proved. In Section 3, we consider the convergence rate of time discretization of MT-FPDEs, based on the Diethelm fractional backward difference method (DFBDM). In Section 4, we propose an FEM based on the weak formulation and carry out the error analysis. In Section 5, the stability of this method is proven. Finally, the numerical examples are considered for matching well with the main conclusions.

2. Existence and Uniqueness

Let Γ(·) denote the gamma function. For any positive integer n and n − 1 < α < n, the Caputo derivative are the Riemann-Liouville derivative are, respectively, defined as follows [30].

(i)
The left Caputo derivatives:
()
(ii)
The left Riemann-Liouville derivatives:
()
(iii)
The right Riemann-Liouville derivatives:
()

Let C^∞(0, T) denote the space of infinitely differentiable functions on (0, T) and

denote the space of infinitely differentiable functions with compact support in (0, T). We use the expression A≲B to mean that A ≤ cB when c is a positive real number and use the expression A≅B to mean that A≲B≲A. Let L₂(𝒬) be the space of measurable functions whose square is the Lebesgue integrable in 𝒬 which may denote a domain 𝒬 = I × Ω, I or Ω. Here time domain I : = (0, T) and space domain Ω : = (0, X). The inner product and norm of L₂(𝒬) are defined by

()

For any real σ > 0, we define the spaces

and

to be the closure of

with respect to the norms

, and

respectively, where

()

In the usual Sobolev space

, we also have the definition

()

From [3], for σ > 0, σ ≠ n − 1/2, the spaces , , and are equal, and their seminorms are all equivalent to . We first recall the following results.

Lemma 1 (see [3].)Let 0 < θ < 2, θ ≠ 1. Then for any , then

()

From [3], we define the following space:

()

Here B^α/2(I × Ω) is a Banach space with respect to the following norm:

()

where

, endowed with the norm

()

Based on the relation equation between the left Caputo and the Riemann-Liouville derivative in [31], we can translate the Caputo problem to the Riemann-Liouville problem. Then, we consider the weak formulation of (1) as follows. For f ∈ B^α/2(I×Ω)^′, find u(t, x) ∈ B^α/2(I × Ω) such that

()

where the bilinear form is, by Lemma 1,

()

and the functional is

Based on the main results in Subsection 3.2 in [32], we can prove the following existence and uniqueness theorem.

Theorem 2. Assume that 0 < α < 1 and . Then the system (17) has a unique solution in B^α/2(I × Ω). Furthermore,

()

Proof. The existence and uniqueness of the solution of (17) is guaranteed by the well-known Lax-Milgram theorem. The continuity of the bilinear form 𝒜 and the functional ℱ is obvious. Now we need to prove the coercivity of 𝒜 in the space B^α/2(I × Ω). From the equivalence of , and , for all u, v ∈ B^α/2(I × Ω), using the similar proof process in [32], we obtain

()

Then we take v = u in (17) to get

by the Schwarz inequality and the Poincaré inequality.

3. Time Discretization and Convergence

In this section, we consider DFBDM for the time discretization of (1)–(3), which is introduced in [33] for fractional ordinary differential equations. We can obtain the convergence order for the time discretization for the MT-FPDEs. Let A = −Δ_x,

. Let u(t), f(t), and u(0) denote the one-variable functions as u(t, ·), f(t, ·), and u(0, ·), respectively. Then (1) can be written in the abstract form, for 0 < t < T, 0 < α_s < ⋯<α₁ < α < 1, with initial value u(0) = u₀. Now we have

()

Let 0 = t₀ < t₁ < ⋯<t_N = T be a partition of [0, T]. Then, for fixed t_j, j = 1,2, …, N, we have

()

where g(τ) = u(t_j − t_jτ) − u₀. Here, the integral is a Hadamard finite-part integral in [33] and [34].

Now, for every j, we replace the integral by a first-degree compound quadrature formula with equispaced nodes 0, (1/j), (2/j), …, 1 and obtain

()

where the weights

are

()

and the remainder term

satisfies

, where γ_α > 0 is a constant.

Thus, for

, we have

()

Let t = t_j, we can write (21) as

()

Denote U^j as the approximation of u(t_j) and f_j = f(t_j). We obtain the following equation:

()

Lemma 3 (see [34].)For 0 < α < 1, let the sequence {d_j} _j=1,2,… be given by d₁ = 1 and . Then, 1 ≤ d_j ≤ (sin (πα)/πα(1 − α))j^α, for j = 1,2, 3, ….

Let e^j = u(t_j) − U^j denote the error in t_j. Then we have the following error estimate.

Theorem 4. Let U^j and u(t_j) be the solutions of (27) and (21), respectively. Then one has ∥U^j − u(t_j)∥≲Δt^2−α.

Proof. Subtracting (27) from (26), we obtain the error equation

()

Note that e⁰ = u(0) − U⁰ = 0. Denote

()

Let ∥·∥ denote the L₂-norm, then we have

()

Note that A is a positive definite elliptic operator with all of eigenvalues λ > 0. Since and Γ(−α) < 0, we have

()

Hence,

()

Denote d₁ = 1 and

()

where i = 1,2, …, s. By induction and Lemma 3, then we have

()

4. Space Discretization and Convergence

In this section, we will consider the space discretization for MT-FPDEs (1) and show the complete process and details of numerical scheme. The variational form of (1) is to find

, such that, for all

()

Let h denote the maximal length of intervals in Ω and let r be any nonnegative integer. We denote the norm in H^r(Ω) by

. Let

be a family of finite element spaces with the accuracy of order r ≥ 2, that is, S_h consists of continuous functions on the closure

of Ω which are polynomials of degree at most r − 1 in each interval and which vanish outside Ω_h, such that for small h,

()

The semidiscrete problem of (1) is to find the approximate solution u_h(t) = u_h(t, ·) ∈ S_h and

for each t such that

()

Let U^N = u_h(t_N, x). After the time discretization, we have

()

In terms of the basis

, choosing χ = ψ_m, writing

()

and inserting it into (38), one obtains

()

Let

. From (40), we obtain a vector equation

()

where initial condition is U₀ = u(0, x),

is the mass matrix, Ψ₂ is stiffness matrix as

, and

is a vector valued function. Then, we can obtain the solution U_N at t = t_N.

Let R_h : H¹(Ω) → S_h be the elliptic projection, defined by , for all χ ∈ S_h.

Lemma 5 (see [35].)Assume that (36) holds, then with R_h and , we have for 1 ≤ b ≤ r.

In virtue of the standard error estimate for the FEM of MT-FPDEs, one has the following theorem which can be proved easily by Lemma 5 and the similar proof in [35].

Theorem 6. For 0 < α_s < ⋯<α₁ < α < 1, let u_h ∈ S_h and be, respectively, the solutions of (37) and (1), then .

5. Stability of the Numerical Method

In this section, we analyze the stability of the FEM for MT-FPEDs (1)–(3). Now we do some preparations before proving the stability of the method. Based on the definition of coefficients in Section 3, we can obtain the following lemma easily.

Lemma 7. For 0 < α < 1, the coefficients , (k = 1, …, j) satisfy the following properties:

(i)
and for k = 1,2, …, j,
(ii)
.

Now we report the stability theorem of this FEM for MT-FPDEs in this section as follows.

Theorem 8. The FEM defined as in (38) is unconditionally stable.

Proof. In (38), let χ(·) = U^j(·) at t = t_j and the right hand . We have

()

Using, Cauchy-Schwarz inequality, for k = 0,1, 2, …, N and Lemma 7, we get

()

We prove the stability of (37) by induction. Since when j = 1, we have

()

The induction basis

is presupposed. For the induction step, we have

. Then using this result, by Lemma 7, we obtain

()

Here 0 < 1 − α < 1. After squaring at both sides of the above inequality, we obtain .

6. Numerical Experiments

In this section, we present the numerical examples of MT-FPDEs to demonstrate the effectiveness of our theoretical analysis. The main purpose is to check the convergence behavior of numerical solutions with respect to Δt and Δx, which have been shown in Theorem 4 and Theorem 6. It is noted that the method in [29] is a special case of the method in our paper for fractional partial differential equation with single fractional order. So, we just need to compare FEM in our paper with other existing methods in [8, 28].

Example 9. For t ∈ [0, T], x ∈ (0,1), consider the MT-FPDEs with two variables as follows:

()

where the right-side function f(t, x) = (2t^2−α/Γ(3 − α))sin(2πx) + (2t^2−β/Γ(3 − β))sin(2πx) + 4π²sin(2πx)t². The exact solution is u(t, x) = t²sin(2πx).

We use this example to check the convergence rate (c. rate) and CPU time (CPUT) of numerical solutions with respect to the fractional orders α and β.

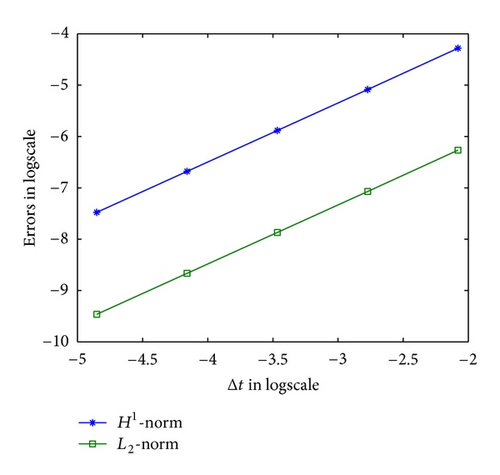
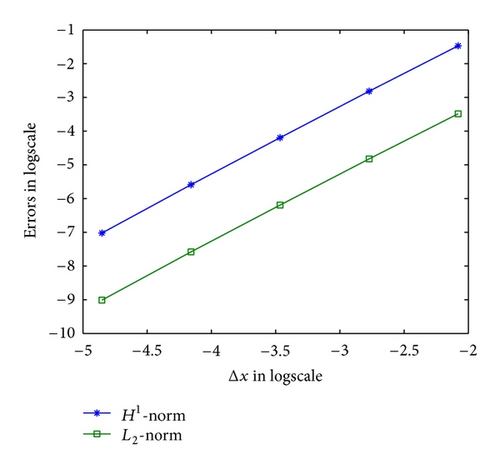
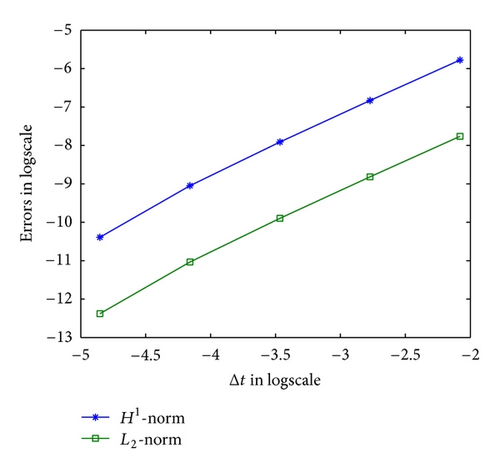
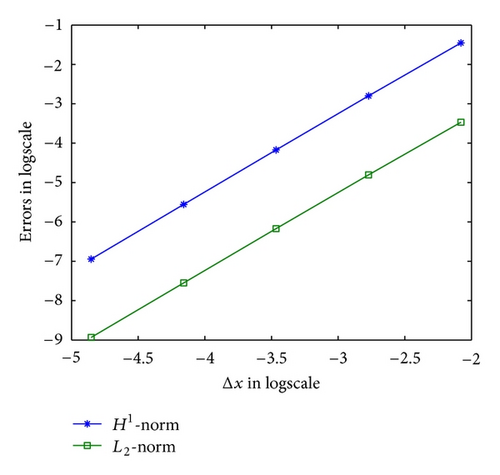
In the first test, we fix T = 1, α = 0.9 and β = 0.5 and choose Δx = 0.001 which is small enough such that the space discretization errors are negligible as compared with the time errors. Choosing Δt = 1/2ⁱ (i = 2,4, …, 7), we report that the convergence rate of FDM in time is nearly 1.15 in Table 1, which matches well with the result of Theorem 4. On the other hand, Table 2 shows that an approximate convergence rate is 2, by fixing Δt = 0.001 and choosing Δx = 1/2ⁱ (i = 2, …, 6), which matches well with the result of Theorem 6. In the second test, we give the convergence rate when α = 0.5, β = 0.25 for Δt in Table 3, and Δx in Table 4, respectively. We also report the L₂-norm and H¹-norm of errors in Figures 1 and 2, respectively.

Fixing Δx = 0.001, α = 0.9, and β = 0.3 in (46), we compare the error and CPUT calculated by the FEM in this paper with the FDM in [8] and the FPCM in [8]. From Table 5, it can be seen that the FEM in this paper is computationally effective.

Table 1. Convergence rate in time for (46) with α = 0.9 and β = 0.5.

Δx	Δt	H¹-norm	L₂-norm	c. rate	CPUT (seconds)
0.001	1/4	1.3815 × 10⁻²	1.8960 × 10⁻³		0.214
0.001	1/16	6.1890 × 10⁻³	8.4939 × 10⁻⁴	1.1585	0.357
0.001	1/32	2.7858 × 10⁻³	3.8234 × 10⁻⁴	1.1516	0.736
0.001	1/64	1.2571 × 10⁻³	1.7252 × 10⁻⁴	1.1481	1.438
0.001	1/128	5.6567 × 10⁻⁴	7.7635 × 10⁻⁵	1.1520	2.922

Table 2. Convergence rate in space for (46) with α = 0.9 and β = 0.5.

Δt	Δx	H¹-norm	L₂-norm	c. rate	CPUT (seconds)
0.001	1/4	0.2294	3.0611 × 10⁻²		20.35
0.001	1/16	5.9763 × 10⁻²	8.0381 × 10⁻³	1.9291	21.85
0.001	1/32	1.5067 × 10⁻²	2.0442 × 10⁻³	1.9753	26.68
0.001	1/64	3.7356 × 10⁻³	5.0966 × 10⁻⁴	2.0039	32.72
0.001	1/128	8.9129 × 10⁻⁴	1.2198 × 10⁻⁴	2.0629	41.03

Table 3. Convergence rate in time for (46) with α = 0.5 and β = 0.25.

Δx	Δt	H¹-norm	L₂-norm	c. rate	CPUT (seconds)
0.001	1/4	3.0985 × 10⁻³	4.2525 × 10⁻⁴		0.218
0.001	1/16	1.0789 × 10⁻³	1.4807 × 10⁻⁴	1.5221	0.413
0.001	1/32	3.6702 × 10⁻⁴	5.0372 × 10⁻⁵	1.5556	0.921
0.001	1/64	1.1772 × 10⁻⁴	1.6156 × 10⁻⁵	1.6406	1.855
0.001	1/128	3.0704 × 10⁻⁵	4.2139 × 10⁻⁶	1.6388	3.783

Table 4. Convergence rate in space for (46) with α = 0.5 and β = 0.25.

Δt	Δx	H¹-norm	L₂-norm	c. rate	CPUT (seconds)
0.001	1/4	2.3325 × 10⁻¹	3.1119 × 10⁻²		23.73
0.001	1/16	6.0836 × 10⁻²	8.1823 × 10⁻³	1.9272	26.29
0.001	1/32	1.5382 × 10⁻²	2.0870 × 10⁻³	1.9711	33.49
0.001	1/64	3.8569 × 10⁻³	5.2622 × 10⁻⁴	1.9877	41.68
0.001	1/128	9.6378 × 10⁻⁴	1.3189 × 10⁻⁴	1.9963	55.24

Table 5. Comparison of error and CPUT for (46) with α = 0.9 and β = 0.3.

Δx	Δt	FEM		FDM [8]		FPCM [8]
Δx	Δt	Error	CPUT	Error	CPUT	Error	CPUT
0.001	1/4	3.7056 × 10⁻³	0.238	5.8723 × 10⁻³	0.897	2.2027 × 10⁻²	6.16
0.001	1/8	1.6794 × 10⁻³	0.481	2.6751 × 10⁻³	1.837	8.7467 × 10⁻³	16.63
0.001	1/16	7.6528 × 10⁻⁴	0.962	1.2159 × 10⁻³	3.512	3.4693 × 10⁻³	30.11
0.001	1/32	3.5009 × 10⁻⁴	1.335	5.5190 × 10⁻⁴	7.001	1.3765 × 10⁻³	52.71
0.001	1/64	1.6027 × 10⁻⁴	2.703	2.4997 × 10⁻⁴	14.45	5.4564 × 10⁻⁴	106.49

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

H¹-norm and L₂-norm of errors for (46) with α = 0.9, β = 0.5, Δx = 0.001 (a), and Δt = 0.001 (b).

Example 10. Consider the following multierm fractional differential problem:

()

where f(t) = (4t^1.5/Γ(2.5)) + (12t²/Γ(3.5)). For α = 0.5 and β = 0.3, the exact solution is u(t) = t² + t^2.5.

For the problem (47), our method in this paper is just the DFBDM in Section 3. Therefore, we only need to compare M1 with the FEM in [28] (FEM2). In Table 6, although the convergence rate of FEM2 is higher than that of DFBDM, the error and CPUT of DFBDM are smaller than those of FEM2.

Table 6. Comparison of error, convergence rate, and CPUT for (47) with α = 0.5 and β = 0.3.

Δt	DFBDM (Section 3)			FEM2 [28]
Δt	Error	c. rate	CPUT	Error	c. rate	CPUT
1/4	9.1975 × 10⁻⁴		0.000864	3.6606 × 10⁻³		0.001862
1/8	3.3037 × 10⁻⁴	1.4772	0.001986	7.8173 × 10⁻³	2.2274	0.004902
1/16	1.1375 × 10⁻⁴	1.5382	0.004649	1.6210 × 10⁻⁴	2.2697	0.051816
1/32	3.5112 × 10⁻⁵	1.6958	0.012112	3.2629 × 10⁻⁴	2.3127	0.518130

Acknowledgments

The authors are grateful to the referees for their valuable comments. This work is supported by the National Natural Science Foundation of China (11101109 and 11271102), the Natural Science Foundation of Hei-Long-Jiang Province of China (A201107), and SRF for ROCS, SEM.

References

1 Li C., Zhao Z., and Chen Y., Numerical approximation and error estimates of a time fractional order diffusion equation, Proceedings of the ASME International Design Engineering Technical Conference and Computers and Information in Engineering Conference (IDETC/CIE ′09), 2009, San Diego, Calif, USA.
Google Scholar
2 Jiang Y. and Ma J., High-order finite element methods for time-fractional partial differential equations, Journal of Computational and Applied Mathematics. (2011) 235, no. 11, 3285–3290, https://doi.org/10.1016/j.cam.2011.01.011, MR2784043, ZBL1216.65130.
10.1016/j.cam.2011.01.011
Web of Science® Google Scholar
3 Li X. J. and Xu C. J., Existence and uniqueness of the weak solution of the space-time fractional diffusion equation and a spectral method approximation, Communications in Computational Physics. (2010) 8, no. 5, 1016–1051, https://doi.org/10.4208/cicp.020709.221209a, MR2674276.
10.4208/cicp.020709.221209a
Web of Science® Google Scholar
4 Diethelm K. and Ford N. J., Numerical solution of the Bagley-Torvik equation, Numerical Mathematics. (2002) 42, no. 3, 490–507, MR1931882, ZBL1035.65067.
10.1023/A:1021973025166
Google Scholar
5 Diethelm K. and Ford N. J., Multi-order fractional differential equations and their numerical solution, Applied Mathematics and Computation. (2004) 154, no. 3, 621–640, https://doi.org/10.1016/S0096-3003(03)00739-2, MR2072809, ZBL1060.65070.
10.1016/S0096-3003(03)00739-2
Web of Science® Google Scholar
6 Daftardar-Gejji V. and Bhalekar S., Boundary value problems for multi-term fractional differential equations, Journal of Mathematical Analysis and Applications. (2008) 345, no. 2, 754–765, https://doi.org/10.1016/j.jmaa.2008.04.065, MR2429175, ZBL1151.26004.
10.1016/j.jmaa.2008.04.065
Web of Science® Google Scholar
7 Jiang H., Liu F., Turner I., and Burrage K., Analytical solutions for the multi-term time-space Caputo-Riesz fractional advection-diffusion equations on a finite domain, Journal of Mathematical Analysis and Applications. (2012) 389, no. 2, 1117–1127, https://doi.org/10.1016/j.jmaa.2011.12.055, MR2879284, ZBL1234.35300.
10.1016/j.jmaa.2011.12.055
Web of Science® Google Scholar
8 Liu F., Meerschaert M. M., McGough R. J., Zhuang P., and Liu Q., Numerical methods for solving the multi-term time-fractional wave-diffusion equation, Fractional Calculus and Applied Analysis. (2013) 16, no. 1, 9–25, https://doi.org/10.2478/s13540-013-0002-2, MR3016639.
10.2478/s13540-013-0002-2
CAS PubMed Web of Science® Google Scholar
9 Psihoyios G. and Simos T. E., Trigonometrically fitted predictor-corrector methods for IVPs with oscillating solutions, Journal of Computational and Applied Mathematics. (2003) 158, no. 1, 135–144, https://doi.org/10.1016/S0377-0427(03)00481-3, MR2017373, ZBL1027.65095.
10.1016/S0377-0427(03)00481-3
Web of Science® Google Scholar
10 Simos T. E., Famelis I. T., and Tsitouras C., Zero dissipative, explicit Numerov-type methods for second order IVPs with oscillating solutions, Numerical Algorithms. (2003) 34, no. 1, 27–40, https://doi.org/10.1023/A:1026167824656, MR2015576, ZBL1031.65080.
10.1023/A:1026167824656
Web of Science® Google Scholar
11 Simos T. E., Dissipative trigonometrically-fitted methods for linear second-order IVPs with oscillating solution, Applied Mathematics Letters. (2004) 17, no. 5, 601–607, https://doi.org/10.1016/S0893-9659(04)90133-4, MR2057357, ZBL1062.65075.
10.1016/S0893-9659(04)90133-4
Web of Science® Google Scholar
12 Psihoyios G. and Simos T. E., A fourth algebraic order trigonometrically fitted predictor-corrector scheme for IVPs with oscillating solutions, Journal of Computational and Applied Mathematics. (2005) 175, no. 1, 137–147, https://doi.org/10.1016/j.cam.2004.06.014, MR2107275, ZBL1063.65060.
10.1016/j.cam.2004.06.014
Web of Science® Google Scholar
13 Stavroyiannis S. and Simos T. E., Optimization as a function of the phase-lag order of nonlinear explicit two-step P.-stable method for linear periodic IVPs, Applied Numerical Mathematics. (2009) 59, no. 10, 2467–2474, https://doi.org/10.1016/j.apnum.2009.05.004, MR2553148.
10.1016/j.apnum.2009.05.004
Web of Science® Google Scholar
14 Panopoulos G. A. and Simos T. E., An optimized symmetric 8-Step semi-embedded predictor-corrector method for IVPs with oscillating solutions, Applied Mathematics & Information Sciences. (2013) 7, no. 1, 73–80.
10.12785/amis/070107
Web of Science® Google Scholar
15 Konguetsof A. and Simos T. E., A generator of hybrid symmetric four-step methods for the numerical solution of the Schrödinger equation, Journal of Computational and Applied Mathematics. (2003) 158, no. 1, 93–106, https://doi.org/10.1016/S0377-0427(03)00469-2, MR2013608, ZBL1027.65094.
10.1016/S0377-0427(03)00469-2
Web of Science® Google Scholar
16 Kalogiratou Z., Monovasilis Th., and Simos T. E., Symplectic integrators for the numerical solution of the Schrödinger equation, Journal of Computational and Applied Mathematics. (2003) 158, no. 1, 83–92, https://doi.org/10.1016/S0377-0427(03)00478-3, MR2013607, ZBL1027.65171.
10.1016/S0377-0427(03)00478-3
Web of Science® Google Scholar
17 Sakas D. P. and Simos T. E., Multiderivative methods of eighth algebraic order with minimal phase-lag for the numerical solution of the radial Schrödinger equation, Journal of Computational and Applied Mathematics. (2005) 175, no. 1, 161–172, https://doi.org/10.1016/j.cam.2004.06.013, MR2107277, ZBL1063.65067.
10.1016/j.cam.2004.06.013
Web of Science® Google Scholar
18 Simos T. E., Exponentially and trigonometrically fitted methods for the solution of the Schrödinger equation, Acta Applicandae Mathematicae. (2010) 110, no. 3, 1331–1352, https://doi.org/10.1007/s10440-009-9513-6, MR2639174, ZBL1192.65111.
10.1007/s10440-009-9513-6
Web of Science® Google Scholar
19 Simos T. E., Optimizing a hybrid two-step method for the numerical solution of the Schrödinger equation and related problems with respect to phase-lag, Journal of Applied Mathematics. (2012) 2012, 17, 420387, https://doi.org/10.1155/2012/420387, MR2904539, ZBL1247.65096.
10.1155/2012/420387
Google Scholar
20 Anastassi Z. A. and Simos T. E., A parametric symmetric linear four-step method for the efficient integration of the Schrödinger equation and related oscillatory problems, Journal of Computational and Applied Mathematics. (2012) 236, no. 16, 3880–3889, https://doi.org/10.1016/j.cam.2012.03.016, MR2926248, ZBL1246.65105.
10.1016/j.cam.2012.03.016
Web of Science® Google Scholar
21 Tselios K. and Simos T. E., Runge-Kutta methods with minimal dispersion and dissipation for problems arising from computational acoustics, Journal of Computational and Applied Mathematics. (2005) 175, no. 1, 173–181, https://doi.org/10.1016/j.cam.2004.06.012, MR2107278, ZBL1063.65113.
10.1016/j.cam.2004.06.012
Web of Science® Google Scholar
22 Anastassi Z. A. and Simos T. E., An optimized Runge-Kutta method for the solution of orbital problems, Journal of Computational and Applied Mathematics. (2005) 175, no. 1, 1–9, https://doi.org/10.1016/j.cam.2004.06.004, MR2105665, ZBL1063.65059.
10.1016/j.cam.2004.06.004
Web of Science® Google Scholar
23 Papadopoulos D. F. and Simos T. E., A modified Runge-Kutta-Nyström method by using phase lag properties for the numerical solution of orbital problems, Applied Mathematics & Information Sciences. (2013) 7, no. 2, 433–437.
10.12785/amis/070202
Web of Science® Google Scholar
24 Monovasilis T., Kalogiratou Z., and Simos T. E., Exponentially fitted symplectic Runge-Kutta-Nyström methods, Applied Mathematics & Information Sciences. (2013) 7, no. 1, 81–85.
10.12785/amis/070108
Web of Science® Google Scholar
25 Kalogiratou Z. and Simos T. E., Newton-Cotes formulae for long-time integration, Journal of Computational and Applied Mathematics. (2003) 158, no. 1, 75–82, https://doi.org/10.1016/S0377-0427(03)00479-5, MR2013606, ZBL1041.65104.
10.1016/S0377-0427(03)00479-5
Web of Science® Google Scholar
26 Simos T. E., Closed Newton-Cotes trigonometrically-fitted formulae of high order for long-time integration of orbital problems, Applied Mathematics Letters. (2009) 22, no. 10, 1616–1621, https://doi.org/10.1016/j.aml.2009.04.008, MR2561745, ZBL1171.65449.
10.1016/j.aml.2009.04.008
Web of Science® Google Scholar
27 Simos T. E., New stable closed Newton-Cotes trigonometrically fitted formulae for long-time integration, Abstract and Applied Analysis. (2012) 2012, 15, 182536, https://doi.org/10.1155/2012/182536, MR2922913, ZBL1242.65026.
10.1155/2012/182536
Google Scholar
28 Badr A. A., Finite element method for linear multiterm fractional differential equations, Journal of Applied Mathematics. (2012) 2012, 9, 482890, https://doi.org/10.1155/2012/482890.
10.1155/2012/482890
Google Scholar
29 Ford N. J., Xiao J., and Yan Y., A finite element method for time fractional partial differential equations, Fractional Calculus and Applied Analysis. (2011) 14, no. 3, 454–474, https://doi.org/10.2478/s13540-011-0028-2, MR2837641.
10.2478/s13540-011-0028-2
Web of Science® Google Scholar
30 Podlubny I., Fractional Differential Equations, 1999, 198, Academic Press, San Diego, Calif, USA, MR1658022.
Web of Science® Google Scholar
31 Samko S. G., Kilbas A. A., and Marichev O. I., Fractional Integrals and Derivatives: Theory and Applications, 1993, Gordon and Breach Science, Philadelphia, Pa, USA, MR1347689.
Google Scholar
32 Li X. J. and Xu C. J., A space-time spectral method for the time fractional diffusion equation, SIAM Journal on Numerical Analysis. (2009) 47, no. 3, 2108–2131, https://doi.org/10.1137/080718942, MR2519596, ZBL1193.35243.
10.1137/080718942
Web of Science® Google Scholar
33 Diethelm K., An algorithm for the numerical solution of differential equations of fractional order, Electronic Transactions on Numerical Analysis. (1997) 5, no. 1, 1–6, MR1447831, ZBL0890.65071.
Google Scholar
34 Diethelm K., Generalized compound quadrature formulae for finite-part integrals, IMA Journal of Numerical Analysis. (1997) 17, no. 3, 479–493, https://doi.org/10.1093/imanum/17.3.479, MR1459334, ZBL0871.41021.
10.1093/imanum/17.3.479
Web of Science® Google Scholar
35 Thomée V., Galerkin Finite Element Methods for Parabolic Problems, 2006, Springer, Berlin, Germany, MR2249024.
Google Scholar

All articles

Stability and Convergence of an Effective Finite Element Method for Multiterm Fractional Partial Differential Equations

Abstract

1. Introduction

2. Existence and Uniqueness

3. Time Discretization and Convergence

4. Space Discretization and Convergence

5. Stability of the Numerical Method

6. Numerical Experiments

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Stability and Convergence of an Effective Finite Element Method for Multiterm Fractional Partial Differential Equations

Abstract

1. Introduction

2. Existence and Uniqueness

3. Time Discretization and Convergence

4. Space Discretization and Convergence

5. Stability of the Numerical Method

6. Numerical Experiments

Acknowledgments

References

Figures

References

Related

Information