Volume 2013, Issue 1 802859

Research Article

Open Access

Generalized Outer Synchronization between Complex Networks with Unknown Parameters

Di Ning,

Di Ning

School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China whu.edu.cn

School of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China scuec.edu.cn

Search for more papers by this author

Xiaoqun Wu,

Corresponding Author

Xiaoqun Wu

[email protected]

orcid.org/0000-0001-5065-6460

School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Jun-an Lu,

Jun-an Lu

School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Hui Feng,

Hui Feng

School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Di Ning,

Di Ning

School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China whu.edu.cn

School of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074, China scuec.edu.cn

Search for more papers by this author

Xiaoqun Wu,

Corresponding Author

Xiaoqun Wu

[email protected]

orcid.org/0000-0001-5065-6460

School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Jun-an Lu,

Jun-an Lu

School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

Hui Feng,

Hui Feng

School of Mathematics and Statistics, Wuhan University, Wuhan 430072, China whu.edu.cn

Search for more papers by this author

First published: 26 December 2013

https://doi.org/10.1155/2013/802859

Citations: 5

Academic Editor: Massimo Furi

Share a link

Email
Wechat
Bluesky

Abstract

As is well known, complex networks are ubiquitous in the real world. One network always behaves differently from but still coexists in balance with others. This phenomenon of harmonious coexistence between different networks can be termed as “generalized outer synchronization (GOS).” This paper investigates GOS between two different complex dynamical networks with unknown parameters according to two different methods. When the exact functional relations between the two networks are previously known, a sufficient criterion for GOS is derived based on Barbalat′s lemma. If the functional relations are not known, the auxiliary-system method is employed and a sufficient criterion for GOS is derived. Numerical simulations are further provided to demonstrate the feasibility and effectiveness of the theoretical results.

1. Introduction

The past decade has seen many important achievements in the research of synchronization of complex networks. Most of this research has been focused on the coherent behavior within a network, where all the nodes within a network arrive at the same steady state [1–7]. This kind of synchronization, which was termed as “inner synchronization” [8], has attracted wide attention. However, in many real-world complex networks, there exist other kinds of synchronization, such as “outer synchronization” between two networks [8, 9], where the “complete outer synchronization” was studied under the assumption that all individuals in two networks have exactly identical dynamics. However, this kind of assumption may seem impractical. Take the predator-prey interactions in ecological communities as an example, where predators and preys influence one another’s behaviors. Without preys there would not be predators, while too many predators would bring the preys into extinction. The networks of predators and preys will finally reach harmonious coexistence without any man-made sabotage. It is worth noting that inside the networks of predators or preys, one individual always behaves differently from another. Thus it is more practical to assume that the nodes have different dynamics. Furthermore, the interaction patterns of predators themselves usually differ from those of preys; that is to say, the topological structure of the predators community is different from that of the preys community. There are a great many examples about harmonious coexistence between different real-world networks.

This kind of coexistence between different dynamical networks is termed as “generalized outer synchronization” [10], which represents another degree of coherence. As is known, due to parameter variation, various dynamics, or random perturbations, one individual always behaves differently from but still coexists in balance with others. That is to say, generalized synchronization widely exists. Particularly, it plays an important role in engineering networks [11–13], biological systems [10], social activities, and many other fields. Therefore, it is necessary and significant to investigate this kind of relationships between different dynamical networks.

In general, the methods to achieve GS can be divided into two classes. One approach is to design control laws to force coupled systems to satisfy a prescribed functional relation. But this approach has the disadvantage that the designed controllers are usually quite complicated and thus difficult to implement in real applications. The other is the auxiliary-system approach, proposed by Abarbanel et al. [2], which makes an identical duplication of the response system that is driven by the same driving signal, as shown below:

()

where x, y, z ∈ Rⁿ are, respectively, the states of the drive, response, and auxiliary systems. GS between x(t) and y(t) occurs if lim _t→∞∥y(t) − z(t)∥ = 0 for any initial conditions y(t₀) ≠ z(t₀), that is, if the response system and the auxiliary system achieve complete synchronization (CS). This method has been widely used in many fields and also extended to the area of complex networks [14–16]. It is noticed that it fails to decide what kind of functional relations exists between each other when nodes of the network achieve GS. However, if the purpose is only to show that there exists GS on networks rather than the exact functional relations, this approach is efficient for investigation of GS on complex networks.

Some recent work [10, 17–23] has studied generalized outer synchronization (GOS) in complex networks or complex systems, where the node dynamics parameters are known in advance. Nevertheless, in many practical situations, it is common that some system parameters cannot be exactly known in prior, and the synchronization will be destroyed and broken by the effects of these uncertainties.

Motivated by the above discussions, generalized outer synchronization between two dynamical networks with unknown parameters is investigated, where nodes in the two networks may have identical or different dynamics and the topological structures are different. Since the functional relations may be previously known or unknown, two kinds of generalized synchronization are considered.

The paper is organized as follows. In Section 2, GOS between two networks with predefined functional relations is investigated and the theoretical result is presented. In Section 3, based on the auxiliary-system method, GOS with unknown functional relations is studied. In Section 4, various numerical simulations are provided to demonstrate the feasibility and effectiveness of the theoretical results. A brief conclusion is drawn in Section 5.

2. GOS with Predefined Functional Relations

Consider the following complex dynamical network consisting of N nonidentical nodes as the drive network, which is described by

()

Here, x_i(t) = (x_i1, …, x_in) ^T ∈ Rⁿ is the state vector of the ith node, A_ix_i(t) + f_i(x_i(t), t) + F_i(x_i(t))α represents the node dynamics, α is the unknown parameter vector, P ∈ R^n×n is the inner-coupling matrix determining the interaction of variables, and B = (b_ij) _N×N is the coupling configuration matrix representing the coupling strength and the topological structure of the network, in which b_ij is defined as follows: if there is a connection from node j to node i(j ≠ i), b_ij ≠ 0; otherwise, b_ij = 0. The diagonal elements of matrix B are defined as

()

Consider another complex network which will be referred to as the response network with a different topological structure and nonidentical node dynamics as follows:

()

where y_i(t) = (y_i1, …, y_im) ^T ∈ R^m is the state vector of node i,

represents the node dynamics which contains the unknown parameter vector β, u_i(i = 1,2, …, N) are the controllers to be designed, and the other notations convey similar meanings as those in the drive network.

Definition 1. Let ϕ_i : Rⁿ → R^m(i = 1,2, …, N) be continuously differentiable vector maps. The two networks (2) and (4) are said to achieve asymptotical generalized outer synchronization if

()

Assumption 2 (global Lipschitz condition). Suppose that there exist nonnegative constants L_i (i = 1,2, …, N), such that for any time-varying vectors x(t), y(t) ∈ R^m, one has

()

where ∥·∥ denotes the 2-norm throughout the paper.

When the functional relations ϕ_i : Rⁿ → R^m(i = 1,2, …, N) are known, one arrives at the following theorem with the network models given above.

Theorem 3. Suppose that Assumption 2 holds. The dynamical networks (2) and (4) reach generalized outer synchronization as defined in Definition 1 with the following controllers:

()

and updating laws

()

where r₁ and r₂ are positive constants, and Dϕ_i(x_i) is the Jacobian matrix of the map ϕ_i(x_i).

Proof. Define e_i = y_i − ϕ_i(x_i). From (2) and (4), one has

()

where e_i = (e_i1, e_i2, …, e_im) ^T ∈ R^m.

Consider the following Lyapunov candidate function:

()

The derivative of V along the trajectory of (9) is

()

Denote L = max {L_i∣i = 1,2, …, N}. Let , , 𝒬 = C ⊗ Q, and let λ_m(·) be the largest eigenvalue of the matrix. Thus one has

()

Let

()

one obtains

()

Obviously, , so V(t) is uniformly continuous. Furthermore, V(t) ≤ V(0)e^−2t; that is, exists, then V(t) is integrable on [0, +∞]. According to Barbalat’s lemma, one gets lim _t→∞V(t) = 0, thus lim _t→∞e_i(t) = 0 for i = 1,2, …, N. That is, networks (2) and (4) achieve generalized outer synchronization asymptotically. This completes the proof.

3. GOS with Unknown Functional Relations

The preceding section focuses on GOS between networks (2) and (4) with previously known relations y_i = ϕ_i(x_i), i = 1,2, …, N. However, the functional relations are sometimes unknown. For this case, one has to refer to the auxiliary-system method proposed by Kocarev and Parlitz [24]. According to the method, one can make a replica for each system in the response network (4), which results in the following network:

()

where z_i ∈ R^m. The drive network (2) and the response network (4) are said to achieve generalized outer synchronization; if the response network (4) and the auxiliary network (15) reach complete outer synchronization, that is, lim _t→∞ ∥z_i(t) − y_i(t)∥ = 0 for any initial conditions y_i(0) ≠ z_i(0)(i = 1,2, …, N).

Assumption 4 (global Lipschitz condition). Suppose that there exist nonnegative constants , such that

()

holds for any time-varying vectors y(t), z(t) ∈ R^m, where β^* is the parameter vector.

Theorem 5. Suppose that Assumptions 2 and 4 hold. Using the following controllers:

()

and updating laws

()

then the drive network (2) and the response network (4) reach generalized outer synchronization.

Proof. According to the auxiliary-system method, networks (2) and (4) achieve generalized outer synchronization if networks (4) and (15) reach complete outer synchronization. Define the synchronization error between (4) and (15) for the ith node as e_i = z_i − y_i. Then the error dynamical systems can be described by

()

Let u(x_i, z_i) = −k(z_i − x_i) and u(x_i, y_i) = −k(y_i − x_i). Then the error dynamical systems can be rewritten into

()

where i = 1,2, …, N.

Consider the following Lyapunov candidate function:

()

The derivative of V along the trajectory of (20) is

()

where L = max (L₁, L₂, …, L_n) and

Let e, 𝒜, 𝒬, and λ_m(·) have the same meaning as that in the proof of Theorem 3, then it turns out

()

Taking

()

one obtains

()

According to Barbalat’s lemma, networks (4) and (15) achieve complete outer synchronization; that is, networks (2) and (4) achieve generalized outer synchronization. This completes the proof.

4. Numerical Simulations

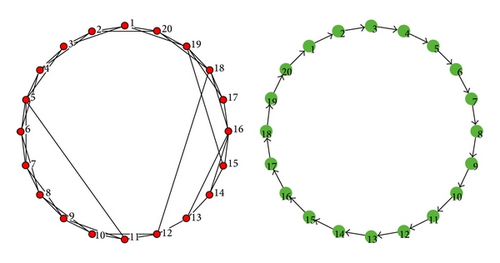
In this section, numerical simulations are carried out on networks consisting of 20 nodes to verify the effectiveness of the control schemes obtained in the preceding sections. Watts-Strogatz (WS) [25] algorithm is employed here to generate a small-world network. Specifically, start from a ring-shaped network with 20 nodes, with each node connecting to its 4 nearest neighbors. Then, rewire each edge in such a way that the beginning end of the edge is kept but the other end is disconnected with probability p and reconnected to another node randomly chosen from the network. In all the following simulations, a WS small-world network generated with rewiring probability p = 0.1, as shown in the left panel of Figure 1, is used as the topological structure for the drive network. Moreover, a directed ring network is employed as the structure of the response network, as shown in the right panel of Figure 1. The weight for every existent edge is supposed to be 0.01. For brevity, the inner-coupling matrices P and Q are taken as identity matrices with proper dimensions.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

A 20-node network generated using the WS small-world algorithm, where the rewiring probability p = 0.1 (left); a 20-node directed ring network (right).

4.1. GOS with Known Functional Relations

4.1.1. GOS with Identical Node Dynamics

In this subsection, it is supposed that nodes in the drive and response networks have the same dynamics described by the well-known Lorenz system [26]:

()

where the parameter vector α = (a,b,c)^⊤ is unknown. Since Lorenz system is chaotic, it is easy to verify that it is bounded. Figure 2 displays a typical Lorenz chaotic attractor.

For a response network (4) consisting of identical Lorenz systems, one has

()

and the unknown parameter vector is β = (l, m, n) ^⊤.

First consider complete outer synchronization between the drive and response networks; that is, the functional relations are

()

The feedback gain k in the controllers is taken as 10, and the gains r₁, r₂ in the updating laws (8) are taken as 10. The left panel of Figure 3 displays the GOS error E(t) between the drive and response networks, where E(t) = 〈∥y_i(t) − x_i(t)∥〉 and 〈·〉 means averaging over all the nodes. One can see from the panel that complete outer synchronization is quickly achieved by employing the control method proposed in Theorem 3. The right panel of Figure 3 shows the estimated evolution of unknown parameters in the drive and response networks. It is obtained that all the estimated parameters evolving with the updating laws (8) tend to some certain constants, which is consistent to the proof of Theorem 3.

Next, consider the following nonlinear functional relations:

()

then

()

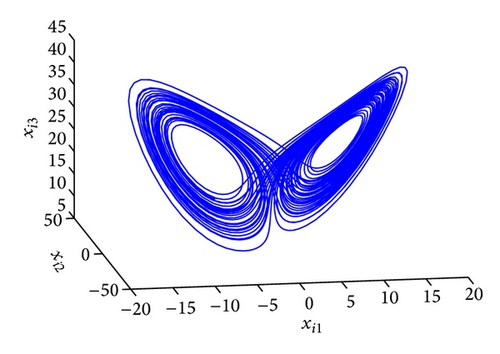
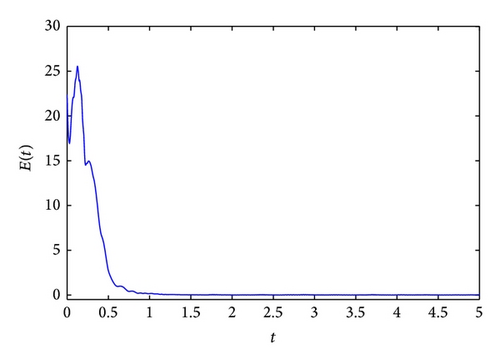
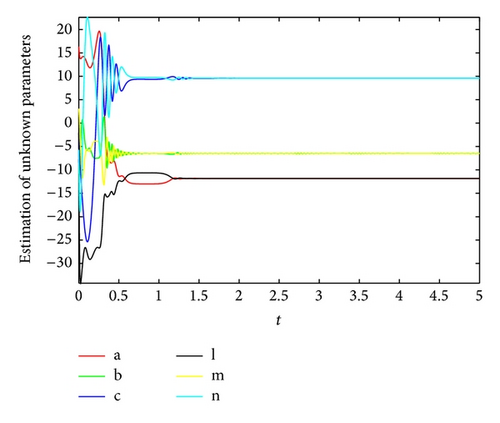
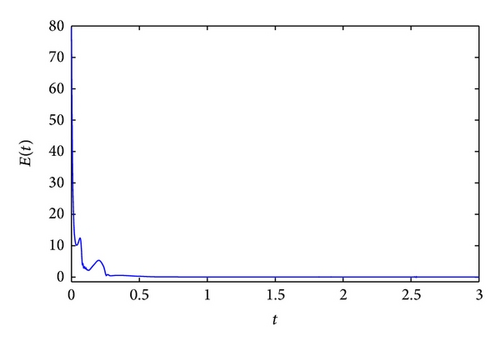
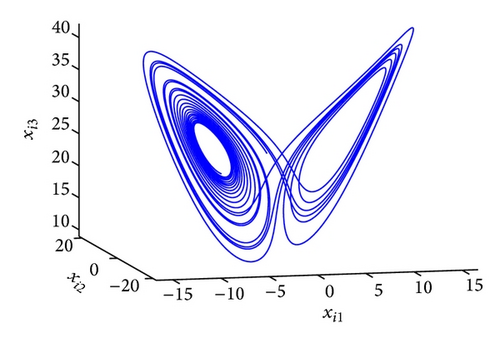
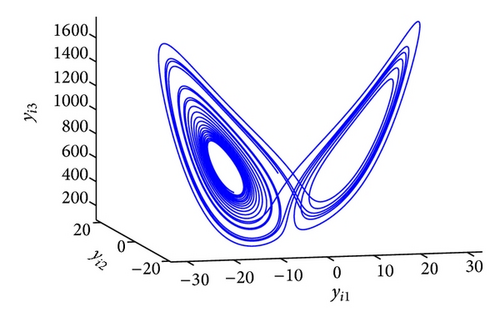
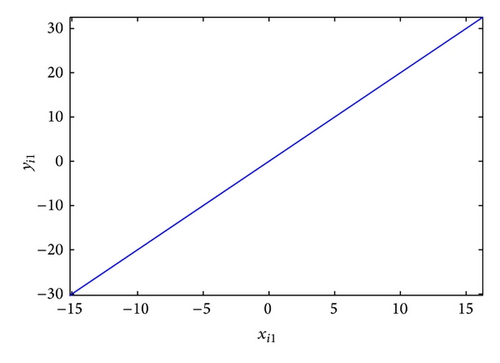
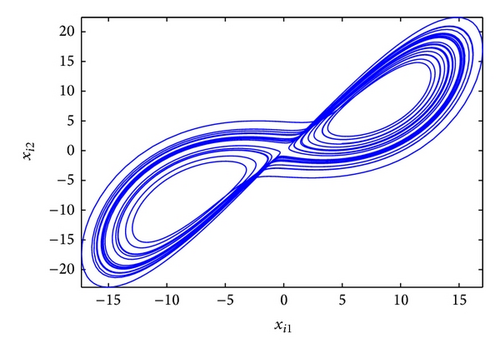
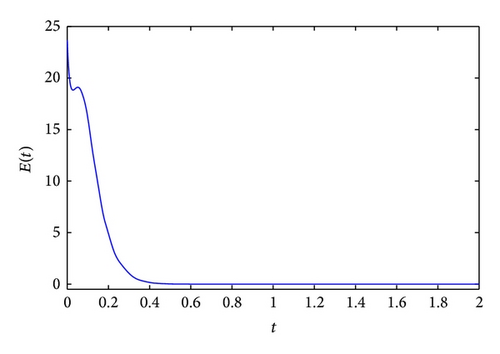
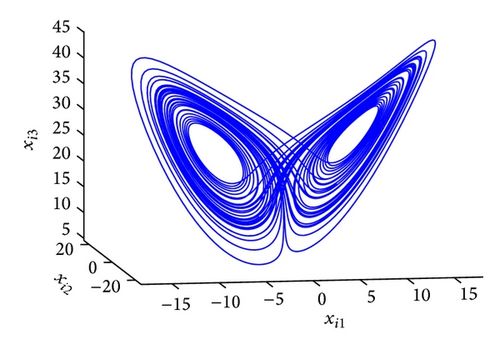
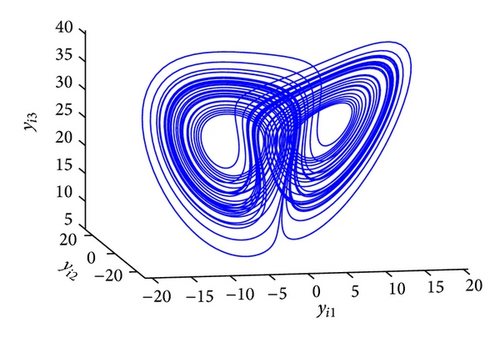
The GOS error E(t) = 〈∥y_i − ϕ_i(x_i)∥〉 between the drive and response networks is displayed in Figure 4. It is obvious that the two networks reach generalized outer synchronization with the proposed controller and updating laws (8). The phase diagrams of node 3 in both networks are displayed in Figure 5. Some corresponding subvariables of node 3 are also depicted in Figure 6, where transients are discarded. The relationships between dynamics of corresponding nodes in the two networks can be clearly observed.

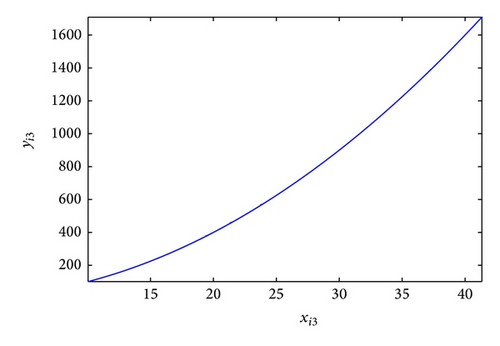
4.1.2. GOS with Different Node Dynamics

In this subsection, the classical Lorenz system is still taken as the node dynamics in the drive network. Chen system [27] is taken as the node dynamics in the response network, which is described by

()

where the parameter vector β = (l, m, n) ^⊤ is supposed to be unknown. A typical Chen attractor is shown in Figure 7.

Let the functional relations be

()

Thus

()

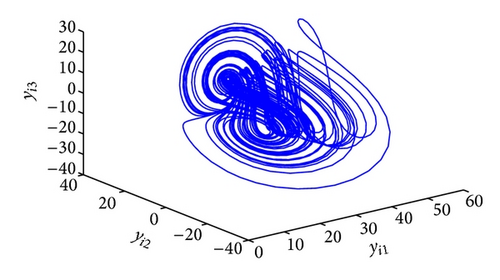
Figure 8 displays the GOS error E(t) = 〈∥y_i(t) − ϕ_i(x_i(t))∥〉 between the two different networks, with k = 100, r₁ = r₂ = 10. It is obvious that E(t) tends to zero after a short transient period. Figure 9 shows the dynamics of node 3 in the drive and response networks, where projections on different planes are displayed.

4.2. GOS with Unknown Functional Relations

Take the node dynamics in the drive network to be Lorenz system with three unknown parameters and that in the response network to be the classical Chen system with two unknown parameters, as described by

()

Thus in the auxiliary network, the node dynamics is

()

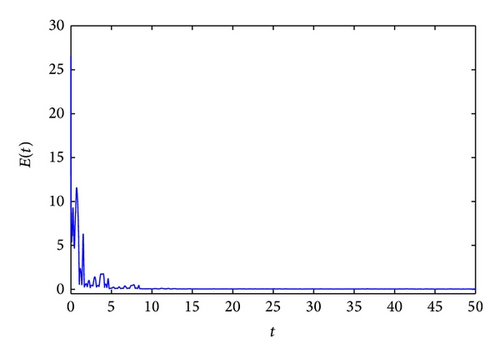
Let k = 20 in the controllers (17), and r = 10 in the updating laws (18). Figure 10 displays the synchronization error between the response and auxiliary networks, where E(t) = 〈∥z_i(t) − y_i(t)∥〉. One can see that when the control is imposed, the synchronization error quickly tends to zero, which means the existence of generalized outer synchronization between the drive and response networks. Figure 11 plots the dynamics of node 3 in the drive and response networks.

5. Conclusions

Research on generalized outer synchronization between complex networks has attracted wide attention in the past few years. To the best of our knowledge, few works focused on the case that the node dynamics parameters are unknown. In this paper, the generalized outer synchronization between two complex dynamical networks with unknown parameters has been investigated, with previously known or unknown functional relations. The feasibility and applicability of the theoretical findings have been validated by numerical simulations.

Acknowledgments

This work was supported in part by the National Natural Science Foundations of China (Grant nos. 61174028, 11172215, and 91130022) and in part by the Fundamental Research Funds for the Central Universities (Grant no. CZQ11010).

References

1 Pecora L. M. and Carroll T. L., Synchronization in chaotic systems, Physical Review Letters. (1990) 64, no. 8, 821–824, https://doi.org/10.1103/PhysRevLett.64.821, MR1038263, ZBL0938.37019.
10.1103/PhysRevLett.64.821
CAS PubMed Web of Science® Google Scholar
2 Pecora L. M. and Carroll T. L., Master stability functions for synchronized coupled systems, Physical Review Letters. (1998) 80, no. 10, 2109–2112, 2-s2.0-4243241129.
10.1103/PhysRevLett.80.2109
CAS Web of Science® Google Scholar
3 Barahona M. and Pecora L. M., Synchronization in small-world systems, Physical Review Letters. (2002) 89, no. 5, 4, 054101, https://doi.org/10.1103/PhysRevLett.89.054101, 2-s2.0-3343010976.
10.1103/PhysRevLett.89.054101
CAS PubMed Web of Science® Google Scholar
4 Chen Y., Rangarajan G., and Ding M., General stability analysis of synchronized dynamics in coupled systems, Physical Review E. (2003) 67, no. 2, 4, 2-s2.0-0038396314, 026209.
10.1103/PhysRevE.67.026209
Web of Science® Google Scholar
5 Wu C. W. and Chua L. O., Synchronization in an array of linearly coupled dynamical systems, IEEE Transactions on Circuits and Systems I. (1995) 42, no. 8, 430–447, https://doi.org/10.1109/81.404047, MR1351879, ZBL0867.93042.
10.1109/81.404047
Web of Science® Google Scholar
6 Lü J. and Chen G., A time-varying complex dynamical network model and its controlled synchronization criteria, IEEE Transactions on Automatic Control. (2005) 50, no. 6, 841–846, https://doi.org/10.1109/TAC.2005.849233, MR2142000.
10.1109/TAC.2005.849233
Web of Science® Google Scholar
7 Zhou J., Lu J., and Lü J., Adaptive synchronization of an uncertain complex dynamical network, IEEE Transactions on Automatic Control. (2006) 51, no. 4, 652–656, https://doi.org/10.1109/TAC.2006.872760, MR2228029.
10.1109/TAC.2006.872760
Web of Science® Google Scholar
8 Li C., Sun W., and Kurths J., Synchronization between two coupled complex networks, Physical Review E. (2007) 76, no. 4, 6, 2-s2.0-35248825562, https://doi.org/10.1103/PhysRevE.76.046204, 046204.
10.1103/PhysRevE.76.046204
CAS PubMed Web of Science® Google Scholar
9 Tang H., Chen L., Lu J., and Tse C. K., Adaptive synchronization between two complex networks with nonidentical topological structures, Physica A. (2008) 387, no. 22, 5623–5630, 2-s2.0-47649131867, https://doi.org/10.1016/j.physa.2008.05.047.
10.1016/j.physa.2008.05.047
Web of Science® Google Scholar
10 Wu X., Zheng W. X., and Zhou J., Generalized outer synchronization between complex dynamical networks, Chaos. (2009) 19, no. 1, 9, 013109, https://doi.org/10.1063/1.3072787, MR2513757.
10.1063/1.3072787
PubMed Web of Science® Google Scholar
11 Rulkov N. F., Sushchik M. M., Tsimring L. S., and Abarbanel H. D. I., Generalized synchronization of chaos in directionally coupled chaotic systems, Physical Review E. (1995) 51, no. 2, 980–994, 2-s2.0-33744833457, https://doi.org/10.1103/PhysRevE.51.980.
10.1103/PhysRevE.51.980
CAS PubMed Web of Science® Google Scholar
12 Suetani H., Iba Y., and Aihara K., Detecting generalized synchronization between chaotic signals: a kernel-based approach, Journal of Physics A. (2006) 39, no. 34, 10723–10742, https://doi.org/10.1088/0305-4470/39/34/009, MR2257784, ZBL1099.37026.
10.1088/0305-4470/39/34/009
Google Scholar
13 Abarbanel H. D. I., Rulkov N. F., and Sushchik M. M., Generalized synchronization of chaos: the auxiliary system approach, Physical Review E. (1996) 53, no. 5, 4528–4535, 2-s2.0-0000388249.
10.1103/PhysRevE.53.4528
CAS Web of Science® Google Scholar
14 Hung Y., Huang Y., Ho M., and Hu C., Paths to globally generalized synchronization in scale-free networks, Physical Review E. (2008) 77, no. 1, 8, 2-s2.0-38349096424, https://doi.org/10.1103/PhysRevE.77.016202, 016202.
10.1103/PhysRevE.77.016202
Web of Science® Google Scholar
15 Guan S., Wang X., Gong X., Li K., and Lai C., The development of generalized synchronization on complex networks, Chaos. (2009) 19, no. 1, 2-s2.0-63849227474, https://doi.org/10.1063/1.3087531, 013130.
10.1063/1.3087531
PubMed Web of Science® Google Scholar
16 Xu X., Chen Z., Si G., Hu X., and Luo P., A novel definition of generalized synchronization on networks and a numerical simulation example, Computers & Mathematics with Applications. (2008) 56, no. 11, 2789–2794, https://doi.org/10.1016/j.camwa.2008.07.036, MR2467666, ZBL1165.34379.
10.1016/j.camwa.2008.07.036
Web of Science® Google Scholar
17 Chen J., Lu J., Wu X., and Zheng W. X., Generalized synchronization of complex dynamical networks via impulsive control, Chaos. (2009) 19, no. 4, 2-s2.0-74349104470, https://doi.org/10.1063/1.3268587, 043119.
10.1063/1.3268587
PubMed Web of Science® Google Scholar
18 Liu H., Chen J., Lu J., and Cao M., Generalized synchronization in complex dynamical networks via adaptive couplings, Physica A. (2010) 389, no. 8, 1759–1770, 2-s2.0-74849084592, https://doi.org/10.1016/j.physa.2009.12.035.
10.1016/j.physa.2009.12.035
CAS Web of Science® Google Scholar
19 Sun Y., Li W., and Ruan J., Generalized outer synchronization between complex dynamical networks with time delay and noise perturbation, Communications in Nonlinear Science and Numerical Simulation. (2013) 18, no. 4, 989–998, https://doi.org/10.1016/j.cnsns.2012.08.040, MR2996611, ZBL1260.93004.
10.1016/j.cnsns.2012.08.040
Web of Science® Google Scholar
20 Wu Y., Li C., Wu Y., and Kurths J., Generalized synchronization between two different complex networks, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 1, 349–355, https://doi.org/10.1016/j.cnsns.2011.04.026, MR2826013, ZBL1243.93039.
10.1016/j.cnsns.2011.04.026
Web of Science® Google Scholar
21 Jia N. and Wang T., Generation and modified projective synchronization for a class of new hyperchaotic systems, Abstract and Applied Analysis. (2013) 2013, 11, 804964, MR3049377, ZBL06209451, https://doi.org/10.1155/2013/804964.
10.1155/2013/804964
Google Scholar
22 He W. and Cao J., Generalized synchronization of chaotic systems: an auxiliary system approach via matrix measure, Chaos. (2009) 19, no. 1, 10, https://doi.org/10.1155/2013/804964, MR2513763.
10.1155/2013/804964
PubMed Web of Science® Google Scholar
23 Peng G., Jiang Y., and Chen F., Generalized projective synchronization of fractional order chaotic systems, Physica A. (2008) 387, no. 14, 3738–3746, 2-s2.0-41649105825, https://doi.org/10.1016/j.physa.2008.02.057.
10.1016/j.physa.2008.02.057
Web of Science® Google Scholar
24 Kocarev L. and Parlitz U., Generalized synchronization, predictability, and equivalence of unidirectionally coupled dynamical systems, Physical Review Letters. (1996) 76, no. 11, 1816–1819, 2-s2.0-0000929946.
10.1103/PhysRevLett.76.1816
CAS PubMed Web of Science® Google Scholar
25 Watts D. and Strogatz S., Collective dynamics of “small-world” networks, Nature. (1998) 393, no. 4, 440–442, https://doi.org/10.1038/30918.
10.1038/30918
CAS PubMed Web of Science® Google Scholar
26 Lorenz E. N., Deterministic nonperiodic flow, Journal of the Atmospheric Sciences. (1963) 20, no. 2, 130–141, https://doi.org/10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2.
10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
Web of Science® Google Scholar
27 Chen G. and Ueta T., Yet another chaotic attractor, International Journal of Bifurcation and Chaos. (1999) 9, no. 7, 1465–1466, https://doi.org/10.1142/S0218127499001024, MR1729683, ZBL0962.37013.
10.1142/S0218127499001024
Web of Science® Google Scholar

Citing Literature

All articles

Generalized Outer Synchronization between Complex Networks with Unknown Parameters

Abstract

1. Introduction

2. GOS with Predefined Functional Relations

3. GOS with Unknown Functional Relations