The main purpose is to investigate both deterministic and stochastic bifurcations of the catalytic CO oxidation. Firstly, super- and subcritical bifurcations are determined by the signs of the Poincaré-Lyapunov coefficients of the center manifold scalar bifurcation equations. Secondly, we explore the stochastic bifurcation of the catalytic CO oxidation on Ir(111) surfaces with multiple delays according to the qualitative changes in the invariant measure, the Lyapunov exponent, and the stationary probability density of system response. Some new criteria ensuring stability and stochastic bifurcation are obtained.

1. Introduction

For most of the practical cases, the dynamical systems will be disturbed by some stochastic perturbation. There are real benefits to be gained in using stochastic rather than deterministic models. It could be intuitively thought that the external noise would smear out the finer details of the nonlinear system, such as bifurcations between well-defined states. However, it could also happen that noise forces the system far away from its deterministic attractors to explore regions of phase space that are otherwise not visited or interact with the nonlinearities giving rise to new phenomena [1–10].

Now, a great care should be taken when reducing the internal/external sources of noise and uncertainties such as thermal noise, observation errors, and model misspecification. The CO oxidation on platinum group crystals offers an experimental setup, where the nonlinear mechanisms have been captured with high accuracy, and sources of internal noise are controlled. The CO oxidation on crystals shows, in the absence of noise, a wide variety of phenomena, for example, oscillations, bistability, bifurcation, excitability, spatiotemporal patterns, and turbulence. These reactions have been receiving an increasing attention as a laboratory analogy of catalysis used at the industrial level to manufacture chemical products and process harmful species. Understanding the effects of external noise on this oxidation reaction can be considered as an effort to bridge the quality gap. Besides material and pressure gap, which have been discussed in the literature before, the quality gap separates small experiments in perfectly controlled settings and the industrial processes that are always under the influence of uncertainties.

In this paper, we investigate the deterministic and stochastic bifurcations of the catalytic CO oxidation on Ir(111) surfaces with multiple delays. Mechanisms and parameters are known with a high degree of accuracy, and the relevant parameters can be controlled. These ideal properties make it possible to go back and forth between theory and experiments. Our paper focuses on homogeneous states and builds on the work of Hayase et al. [11–18] who studied experimentally and numerically the effect of noise on CO oxidation on Ir(111). They verified that the mathematical model was correct and observed probability distributions that are consistent with the presence of multiplicative noise.

The structure of the paper is as follows. In Section 2, we analyzed the single and double Hopf bifurcation of deterministic system. In Section 3, we analyzed the stochastic stability and bifurcation of stochastic system.

2. Deterministic System

In this section, we will investigate the delayed CO oxidation on Ir(111) surfaces as follows:

()

where

is the bifurcation parameter. It is obvious that there is a unique equilibrium point E(0, 1) in system (1).

Let x₁ = u − 0, x₂ = v − 1, and X = [x₁, x₂] ^⊤, then by substituting the corresponding variables in (1), we have

()

Linearized System. As the first step, we analyze the stability of the trivial solution of the linearized system of (1), which is given by

()

in 𝒞 : = 𝒞([−τ, 0], ℜⁿ), and its adjoint form

()

with respect to the associated bilinear relation

()

has eigenvalues λ satisfying the transcendental characteristic equation

()

By the Hopf bifurcation, we let λ_1,2 = ±iω(γ), with, ω(γ) ≠ 0 and ℜe{dΔ(λ, γ)/dγ} ≠ 0, be the eigenvalue of (6). All the remaining eigenvalues of Δ(λ, γ) = 0 have negative real parts. Then, by substituting λ₁ = iω(γ) into Δ(λ, γ) = 0 and setting the real and imaginary parts of the resulting algebraic equations to zero, we have

()

Separating the real and imaginary parts of (7) gives the following equations:

()

or equivalently

()

Possible values of ωτ₁ are of the form ωτ₁ ∈ (2kπ, 2kπ + π/2), k = 0,1, 2, …. Thus, we obtain the bifurcation parameter γ as

()

Now, we compute Hopf’s transversality condition by differentiating implicitly (6) with respect to γ, obtaining

()

Lemma 1. The transversality conditions ℜe(dλ/dγ)_λ=ωi = −ac − bd ≠ 0 hold. If the choice of values for the model parameters is such that the inequality

()

holds.

This means that the pair of eigenvalues λ_1,2 = v(γ) + iω(γ) of Δ(λ, γ) = 0 with v(γ_c) = 0, ω(γ_c) ≠ 0 will cross the imaginary axis from left to right in the complex plane with a nonzero speed as the bifurcation parameter γ varies near its critical value γ_c. Also, it ensures that the steady-state stability of the system is lost at γ = γ_c, and the instability in the sense of supercritical and subcritical bifurcations will persist for larger values of γ. The exact nature of such bifurcations satisfying Hopf’s conditions ((6)–(12)) will depend on the nonlinearity in the delay system.

Rewriting (10) as a quadratic in ω² and letting

, we have

()

whose real and positive solutions are of the form

()

if the following holds

()

In addition, one has to show that the substitution of

and

into (10) will ensure Hopf’s transversality conditions, that is, ℜe(dλ/dγ) _λ=iω. Therefore, with

and ℜe(dλ/dγ) _λ=iω, we obtain

()

By setting ω_min = ω and γ_min = γ, we have

()

These are the minimum values separating the regimes of stable and unstable solutions of the linearized delay equation at the Hopf bifurcation point γ = γ_c, . Below and equal to these minimum values, all the infinite numbers of eigenvalues of the transcendental characteristic equation (6) will lie in the left-hand side of the complex plane.

Next, deriving an expression for τ₁ begins by further rewiring (8) as follows:

()

thus, we obtain

()

and by using the minimum value for

, we get

()

With these minimum values for the gain ω_min, time delay τ_1,k,min, and the response frequency

, one can describe all the critical settings of the model parameters in the delay equation (1) at which the unstable-free oscillation persists. Should unstable oscillations appear at some desired frequency such that

, fine-tuning the model parameters in the vicinity of their critical settings can control such oscillations. To find out whether the bifurcations are supercritical and/or subcritical, we carry out a local center manifold analysis of the nonlinear delay equation (1) as presented in the preceding section.

2.1. The Single Hopf Bifurcation

To obtain the explicit analytical expressions for the stability condition of the Hopf bifurcation solutions (limit cycles), system (1) should be reduced to its center manifold [19–21]. While studying the critical infinite dimensional problem on a two-dimensional center manifold, we begin by defining the elements of the initial continuous function ϕ(θ) ∈ 𝒞 and its projections ϕ^P(θ), ϕ^Q(θ) onto the center and stable subspaces P, Q ∈ 𝒞. For the eigenvalues λ = ±iω, we have ϕ^P(θ) = Φ(θ)b with

, −τ ≤ θ ≤ 0 of the adjoint-generalized eigenspace P ∈ 𝒞 and

, 0 ≤ s ≤ τ, j, k = 1,2 of the adjoint-generalized eigenspace

. The values of the basis Φ(θ) ∈ 𝒞 for P are thus given by

()

and, similarly, the basis

for

is of the form

()

These bases form the inner product matrix

()

in which

()

The substitution of the elements of (Ψ, Φ) _nsg ≠ 0

()

where

()

Then, the basis Ψ(s) for

of the adjoint equation (2) is normalized to

, computing

to yield

()

where the substitution of the new elements (ψ_j(s), ϕ_k(θ)), j, k = 1,2 into (3) will lead to the identity matrix

()

Consequently, the constant matrices B ∈ 𝒞 and are equivalent, and the elements of B at the Hopf bifurcation are B = [[0, ω] ^⊤, [−ω, 0] ^⊤].

With the algebraic simplifications

()

one can easily see that

()

and it follows that J(t, μ)Φ(θ) = Φ(0)e^B(θ+t) is indeed the solution operator of the linearized delay equations in 𝒞. Similarly, we have

, 0 ≤ s ≤ R, and

is the solution operator for the adjoint delay equations in

By the change of variable

with

, we obtain the following as a first-order approximation in ε, for θ = −τ₁, −τ₂:

()

and for θ = 0,

()

Therefore, we obtain (1) of the center manifold as follows:

()

where the perturbation functions Δf⁽¹⁾(z₁, z₂, γ) and Δf⁽²⁾(z₁, z₂, γ) denote the following:

()

Here, the lengthy expressions of c_ij are omitted here, and which in polar coordinate, z₁ = asinθ, z₂ = −acos θ, θ = ωt + φ is equivalent to

()

The so-called Poincaré-Lyapunov coefficient Π⁽¹⁾(τ₁, τ₂, γ) is independently determined by the following formula:

()

As is well known [19–24], the amplitude equation (35) together with (36) can determine the stability behaviour of the center manifold ODEs (33), where all the partial derivatives of Δf⁽¹⁾(z₁, z₂, γ), Δf⁽²⁾(z₁, z₂, γ), for example,

, are evaluated at the bifurcation point (z₁, z₂)→(0,0). Thus, the partial derivatives are given as follows:

()

from which we readily obtain the required values for the formula in (36) as

()

Substituting these quantities into the formulate in (36) will yield

()

This coefficient together with the amplitude bifurcation equation (35) produces the nonlinear bifurcations for multiple delays as shown in the following: (a) Π⁽¹⁾(a, τ₁, τ₂, γ) < 0→ supercritical bifurcation; (b) Π⁽¹⁾(a, τ₁, τ₂, γ) > 0→ subcritical bifurcation.

Theorem 2. Let ac + bd > 0.

(a)
If Π⁽¹⁾(a, τ₁, τ₂, γ) < 0, then system (1) occurs supercritical bifurcation.
(b)
If Π⁽¹⁾(a, τ₁, τ₂, γ) > 0, then system (1) occurs subcritical bifurcation.

2.2. The Double Hopf Bifurcation

For the eigenvalue λ_1,2 = ±iω₁, λ_1,2 = ±iω₂ of the equation Δ(λ, γ) = 0 in (6), we have the base function Φ(θ) = [ϕ₁(θ), ϕ₂(θ), ϕ₃(θ), ϕ₄(θ)], −τ ≤ θ ≤ 0, Ψ(s) = [ψ₁(s), ψ₂(s), ψ₃(s), ψ₄(s)] ^⊤, 0 ≤ s ≤ τ in 𝒞([−τ, 0], ℜⁿ) and 𝒞([−τ, 0], ℜⁿ), accordingly,

()

and they form the inner product matrix (Ψ(s), Φ(θ)) = (ψ_j(s)ϕ_k(θ)), j, k = 1,2, 3,4, namely,

()

The substitution of the elements (Ψ(s), Φ(θ)) = (ψ_j(s)ϕ_k(θ)) into the bilinear pairing (5) and integrating, we obtain the nonsingular matrix

()

where the constant values of this matrix are given by

()

Then,

is normalized to the new basis

, 0 ≤ s ≤ τ, where the elements

, j = 1,2, 3,4 of

are given by

()

Again, the substitution of the elements

, ϕ_k(θ), j, k = 1,2, 3,4 of

will yield the identity matrix, namely,

()

Then, the constant matrix B is given by

()

The change of variable

will yield

()

thereby, for −τ ≤ θ < 0 and τ₁ ≤ τ ≤ τ₂, we have

()

and so

()

The ODEs of the center manifold M_γ ∈ 𝒞([−τ, 0], ℜ⁴) are given by as follows:

()

where the perturbations in these equations denote

()

and the above coefficients in these equations denote the constant values in (52). Here, the lengthy expressions of

and

are omitted here. These equations are further written into the desired standard form of amplitude and phase relations using the polar coordinates z_j = a_jsinθ_j, z_j = a_jcos θ_j, θ_j = ω_jt + φ_j, j = 1,2, 3,4. Again, the application of the integral averaging method to the resulting amplitude and phase equations will yield

()

where the coefficients in these equations are the resulting constant values after averaging. Similarly, the coefficients in these averaged equations, in particular the cubic ones Π⁽¹¹⁾(a, γ), Π⁽²¹⁾(a, γ), will determine whether the double Hopf interactions are of the form (i) subsupercritical bifurcation type, (ii) supersubcritical bifurcation type, (iii) subsubcritical bifurcation type, and (iv) supersupercritical bifurcation type. Like the Poincaré-Lyapunov coefficient Π(a, γ) in (36) for the single Hopf, there are also explicit formulas for computing the double Hopf coefficients Π⁽¹¹⁾(a, γ), Π⁽²¹⁾(a, γ), which are extremely too long to be displayed here. For the account of these formulas for the double Hopf coefficients, again, the publications [22, 23] are excellent references. Classical studies of dynamical systems resulting to equations of the form (53) have demonstrated unprecedented dynamics ranging from global dynamic bifurcations to ultimately chaotic dynamics (see [22, 24]). There exist reliable and robust mathematical tools to examine the long-term behaviour of such dynamics. Campbell et al. [24], in particular, have shown numerically that equations of the form (53) exhibit four double Hopf’s interactions, namely, two super-super-, one super-sub-, and one sub-sub-critical bifurcations. Other interesting dynamics such as large limit cycles, tori, and period doubling were also characterized by the authors.

3. Stochastic System

In the section, we present some preliminary results to be used in a subsequent section to establish the stochastic stability and stochastic bifurcation. Before proving the main theorem, we give some lemmas and definitions.

Definition 3 (see [1] D-bifurcation.)Dynamical bifurcation is concerned with a family of random dynamical systems which is differential and has the invariant measure μ_α. If there exists a constant α_D satisfying in any neighborhood of α_D, there exists another constant α and the corresponding invariant measure ν_α ≠ μ_α satisfying ν_α → μ_α as α → α_D. Then, the constant α_D is a point of dynamical bifurcation.

Definition 4 (see [1] P-bifurcation.)Phenomenological bifurcation is concerned with the change in the shape of density (stationary probability density) of a family of random dynamical systems as the change of the parameter. If there exists a constant α₀ satisfying in any neighborhood of α_D, there exist other two constants α₁, α₂, and their corresponding stationary density functions , satisfying and are not equivalent. Then, the constant α₀ is a point of phenomenological bifurcation.

Definition 5 (see [1] stochastic pitchfork bifurcation.)In the viewpoint of phenomenological bifurcation, the stationary solution of the Fokker-Planck-Kolmogorov (FPK) equation which is corresponded with the stochastic differential equation changes from one peak into two peaks.

In the viewpoint of dynamical bifurcation, there exists a constant μ₀ that satisfies the following conditions:

(i)
when μ < μ₀, the stochastic differential equation has only one invariant measure ν₀; moreover, ν₀ is stable (i.e., the maximal Lyapunov exponent is negative).
(ii)
when μ = μ₀, the invariant measure ν₀ loses its stability and becomes unstable (i.e., the maximal Lyapunov exponent is positive); moreover, the rotation number is zero.
(iii)
when μ > μ₀, the stochastic differential equation has three invariant measures ν₀, ν₁, and ν₂; both ν₁ and ν₂ are stable (i.e., their maximal Lyapunov exponents are both negative).
(iv)
the global attractors of the stochastic differential equation change from a single-point set into a collection of one-dimensional (the closure of the unstable manifold of the unstable invariant measure).

If the stochastic bifurcation of a stochastic differential equation has the above characters, then the stochastic differential equation admits stochastic pitchfork bifurcation at μ = μ₀.

Definition 6 (see [1] the stochastic Hopf bifurcation.)In the viewpoint of phenomenological bifurcation, the stationary solution of the FPK equation which is corresponded to the stochastic differential equation changes from one peak into a crater.

In the viewpoint of dynamical bifurcation, the following can be noticed:

(i)
if one of the invariant measures of the stochastic differential equation loses its stability and becomes unstable (i.e., two Lyapunov exponents are positive), then the rotation number is not zero. Meanwhile, there at least appears one new stable invariant measure,
(ii)
the global attractors of the stochastic differential equation change from a single-point set into a random topological disk (the closure of the unstable manifold of the unstable invariant measure).

If the stochastic bifurcation of a stochastic differential equation has the above characters, then the stochastic differential equation admits the stochastic Hopf bifurcation.

Definition 7 (see [1] stochastically stable.)The trivial solution x(t, t₀, x₀) of stochastic differential equation is said to be stochastically stable or stable in probability if for every pair of ε ∈ (0,1) and α > 0, there exists δ = δ(ε, δ, t₀) > 0 such that

()

whenever |x₀ | < δ. Otherwise, it is said to be stochastically unstable.

In this section, taking some stochastic factors into account, we introduce randomness into the model (1) by replacing the parameters γ by γ → γ + αξ(t). This is only a first step in introducing stochasticity into the model. Ideally, we would also like to introduce stochastic environmental variation into the other parameters such as the transmission coefficient α and δ, but this would make the analysis much too difficult. Hence, we get the following system of stochastic differential equations:

()

Here, ξ(t) is the multiplicative random excitation and the external random excitation directly, and ξ(t) is independent, in possession of zero mean value and standard variance Gaussian white noises, that is, ℰ[ξ(t)] = 0, ℰ[ξ(t)ξ(t + τ)] = δ(τ). Note that the intensity of the noise σ_i (i = 1,2, …, 6),

is the bifurcation parameter. From (3)–(33), we obtain (55) of the stochastic center manifold:

()

Here, the lengthy expressions of c_ij and k_ij are omitted.

Setting the coordinate transformation z₁ = rcos θ, z₂ = rsinθ and by substituting the variable in (34), we obtain

()

It is difficult to calculate the exact solution for system (57) today. According to the Khasminskii limit theorem, when the intensities of the white noises σ_i (i = 1, …, 6) are small enough, the response process {r(t), θ(t)} weakly converged to the two-dimensional Markov diffusion process [1–5]. Through the stochastic averaging method, we obtained the

stochastic differential equation (55) as follows:

()

where W_r(t) and W_θ are the independent and standard Wiener processes. Set the parameter as follows:

()

3.1. Stochastic D-Bifurcation

In the section, we will see how the introduction of randomness changes the stochastic behavior significantly from both the dynamical and phenomenological points of view.

Theorem 8 (D-bifurcation). Let μ₃ = 0, μ₇ = 0. Then, system (55) undergoes stochastic D-bifurcation.

Proof. When μ₃ = 0, μ₇ = 0, Then, system (58) becomes

()

When μ₄ = 0, (60) is a deterministic system, and there is no bifurcation phenomenon. Here, we discuss the situation μ₄ ≠ 0, let

()

The continuous random dynamical system generated by (60) is

()

where ∘dW_r is the differential in the sense of Statonovich, and it is the unique strong solution of (60) with the initial value x. And m(0) = 0, σ(0) = 0, so 0 is a fixed point of φ. Since m(r) is bounded and for any r ≠ 0, it satisfies the ellipticity condition σ(r) ≠ 0. This ensures that there is at most one stationary probability density. According to the Itô equation of amplitude r(t), we obtain its Fokker-Planck-Kolmogorov equation corresponding to (60) as follows:

()

Let ∂p/∂t = 0, then we obtain the solution of system (63)

()

The above equation (63) has two kinds of equilibrium states: fixed point and nonstationary motion. The invariant measure of the former is δ₀, and its probability density is δ_x. The invariant measure of the latter is ν, and its probability density is (64). In the following, we calculate the Lyapunov exponent of the two invariant measures.

Using the solution of linear Itô stochastic differential equation, we obtain the solution of system (60):

()

The Lyapunov exponent with regard to μ of the dynamical system φ is defined as:

()

substituting (65) into (66), note that σ(0) = 0, σ^′(0) = 0, we obtain the Lyapunov exponent of the fixed point:

()

For the invariant measure which regard (65) as its density, we obtain the Lyapunov exponent:

()

Let α = μ₁ + μ₂/8 − μ₄/16. We can obtain that the invariant measure of the fixed point is stable when α < 0, but the invariant measure of the nonstationary motion is stable when α > 0, so α = α_D = 0 is a point of D-bifurcation.

Theorem 9. Let μ₃ = 0, μ₇ = 0. Then, system (55) does not undergo stochastic P-bifurcation.

Proof. By simplifying (64), we can obtain

()

where c is a normalization constant; thus, we have

()

where v = 2(8μ₁ + μ₂ − μ₄)/μ₄. Obviously, when v < −1, that is, μ₁ + μ₂/8 − μ₄/16 < 0, p_st(r) is a δ function. When −1 < v < 0, that is, μ₁ + μ₂/8 − μ₄/16 > 0, r = 0 is a maximum point of p_st(r) in the state space; thus, the system admits D-bifurcation when v = −1, that is, μ₁ + μ₂/8 − μ₄/16 = 0, is the critical condition of D-bifurcation at the equilibrium point. When v > 0, there is no point that makes p_st(r) has the maximum value; thus, the system does not admits P-bifurcation.

Remark 10. Unfortunately, these two definitions (D-bifurcation and P-bifurcation) do not necessarily yield the same result.

Theorem 11 (stochastic pitchfork bifurcation). Let γακ = 0, μ₃ = 0, μ₇ < 0. Then, system (55) undergoes stochastic pitchfork bifurcation.

Proof. When μ₃ = 0, μ₇ ≠ 0, then (58) can be rewritten as

()

Let α = μ₁ + μ₂/8,

, μ₇ < 0, then the system (71) becomes

()

which is solved by

()

We now determine the domain D_α(t, ω), where D_α(t, ω): = {ϕ ∈ ℜ : (t, ω, ϕ) ∈ D} (D = ℜ × Ω × X) is (in general possibly empty) the set of initial values ϕ ∈ ℜ for which the trajectories still exist at time t and the range R_α(t, ω) of ψ_α(t, ω) : D_α(t, ω) → R_α(t, ω).

We have

()

where

()

where

()

We can now determine that

()

and obtain

()

where

()

The ergodic invariant measures of system (71) are as follows.

(i)
For α ≤ 0, the only invariant measure is .
(ii)
For α > 0, we have the three invariant forward Markov measures, and , where
()

We have . Solving the forward Fokker-Planck-Kolmogorov equation

()

yield

(i)
p_α = δ₀ for all α,
(ii)
for p_α > 0,
()

and

, where

Naturally, the invariant measures are those corresponding to the stationary measures . Hence, all invariant measures are Markov measures.

We determine all invariant measures (necessarily Dirac measure) of local RDS χ generated by the SDE

()

on the state space ℜ, μ₁ + μ₂/8 ∈ ℜ. We now calculate the Lyapunov exponent for each of these measures.

The linearized RDS χ_t = DΥ(t, ω, ϕ)χ satisfies the linearized SDE

()

Hence,

()

Thus, if

is a Υ-invariant measure, its Lyapunov exponent is

()

providing the IC

is satisfied.

(i)
For μ₁ + μ₂/8 ∈ ℜ, the IC for is trivially satisfied, and we obtain
()
So, is stable for μ₁ + μ₂/8 < 0 and unstable for μ₁ + μ₂/8 > 0.
(ii)
For μ₁ + μ₂/8 > 0, is measurable; hence, the density p^α of satisfies the Fokker-Planck-Kolmogorov equation
()

which has the unique probability density solution

()

Since

()

the IC is satisfied. The calculation of the Lyapunov exponent is accomplished by observing that

()

where

()

Hence, by the ergodic theorem

()

finally

()

(iii)
For (μ₁ + μ₂/8) > 0, is measurable. Since
()
thus
()

The two families of densities clearly undergo a P-bifurcation at the parameter value α_P = μ₄/8, which is the same value as the transcritical case, since the SDE linearized at ϕ = 0 is the same in the next section. In both cases, we have a D-bifurcation of the trivial reference measure δ₀ at α_D = 0 and a P-bifurcation of α_P = (μ₁ + μ₂/8) ²/2. Then, system (55) has stochastic pitchfork bifurcation.

3.2. P-Bifurcation

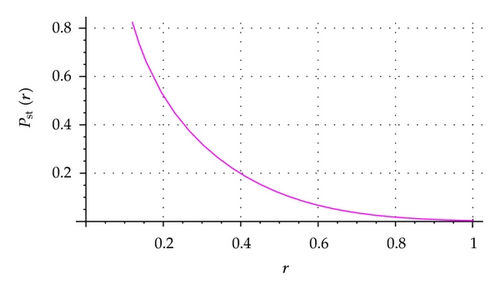
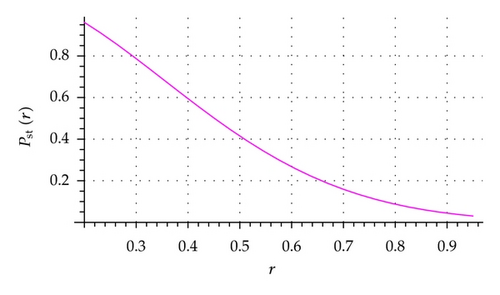
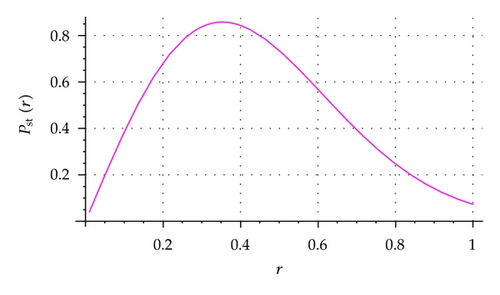
In the following, we investigate the steady-state probability density p_st(r) of the linear Itô stochastic differential equation. Calculating extreme values of the steady-state probability density is one of the most popular efficient methods in studying the bifurcation of a nonlinear dynamical system. The steady-state probability density is an important characteristic value of stochastic bifurcation.

Case I. When μ₃ = 0, μ₇ ≠ 0, then (38) can be rewritten as

()

According to the Itô equation of amplitude r(t), we obtain its Fokker-Planck-Kolmogorov equation form (97) as follows:

()

with the initial value condition μ₇ = 0, p(r, t | r₀, t₀) → δ(r − r₀), t → t₀, where p(r, t | r₀, t₀) is the transition probability density of diffusion process r(t). The invariant measure of r(t) is the steady-state probability density p_st(r) which is the solution of the degenerate system as follows:

()

Through calculation, we can obtain

()

According to Namachivaya’s theory, the extreme value of an steady-state probability density contains the most important essence of the nonlinear stochastic system. In other words, the steady-state probability density can uncover the characteristic information of the steady state. When the intension of the noise tends to zero, the extreme values of p_st(r) approximate to show the behavior of the deterministic system. If the process r(t) is ergodic, then p_st(r) can be regarded as the time measurement for staying in the neighborhood of r(t) according to the Oseledec ergodic theorem.

From the analysis above, if p_st(r) has a maximum value at r^*, the sample trajectory will stay for a longer time in the neighborhood of r^*, that is, r^* is stable in the meaning of probability (with a bigger probability). If p_st(r) has a minimum value (zero), it is just the opposite.

We now calculate the most possible amplitude r^* of system (97), that is, p_st(r) has a maximum value at r^*. So, we have

()

and the solution

. The probabilities and the positions of the Hopf bifurcation occur with different parameter.

Since

()

thus, what we need is

. The conclusion is to go all the way with what has been obtained by the singular boundary theory. The original nonlinear stochastic system has a stochastic Hopf bifurcation at

, where

()

We now choose some values of the parameters in the equations, draw the graphics of p_st(r) (Figure 1). It is worth putting forward that calculating the Hopf bifurcation with the parameters in the original system is necessary. If we now have values of the original parameters in system (55), then α = 0.778205, β = 0.024530, κ = 0.08, γ = 5.640593, δ = 0.200101, σ₁ = 0.1, σ₂ = 0.1, σ₃ = 0.2, σ₄ = 0.3, σ₅ = 0.1, σ₆ = 0.5. After further calculations, we obtain μ₁ = −0.2, μ₂ = 9.5907, μ₃ = 0, μ₄ = 5.1183, μ₇ = −20.4732, then

()

What is more is that

, where p_st(r) has the maximum value.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

P-Bifurcation of system (55) with μ₁ = −0.2, μ₃ = 0, μ₄ = 5.1183, μ₇ = −20.4732; (a) P-bifurcation of p_α(r) at α_p < σ²/2, μ₂ = 5.6, where α = μ₁ + μ₂/8, σ² = −μ₄/μ₇; (b) P-bifurcation of p_α(r) at α_p = σ²/2, μ₂ = 9.5907, where α = (μ₁ + μ₂/8), σ² = −μ₄/μ₇; (c) P-bifurcation of p_α(r) at α_p > σ²/2, μ₂ = 17.6, where α = ν₁/8, σ² = −ν₃/ν₂.

4. Conclusion

In this work, we investigate both the deterministic and stochastic bifurcations of the catalytic CO oxidation on Ir(111) surfaces with multiple delays. By replacing with γ − γ_c, it can be readily seen that the addition of the noise gives rise to a shift in the critical bifurcation point γ_c at the Hopf bifurcation. The results of our computational studies using the Lyapunov exponents and the integral stochastic averaging combined with the Hopf bifurcation produced stability boundaries for structural systems that were much sharper and well defined than those obtained in the earlier stability studies of the same systems. The influence of noise on the reaction-diffusion system model has been studied by the authors [11–18], but explicit and derived conditions for stochastic stability and bifurcation, as the ones displayed here, were not transparent in their publications.

Acknowledgments

This paper was supported by the National Natural Science Foundation of China (no. 11201089) and the Guangxi Natural Science Foundation (no. 2011GXNSFB018065).

References

1 Arnold L., Random Dynamical Systems, 1998, Springer, New York, NY, USA, MR1723992, ZBL1116.01326.
10.1007/978-3-662-12878-7
Google Scholar
2 Mao X., Stochastic Differential Equations and their Applications, 1997, Horwood Publishing, Chichester, UK, MR1475218, ZBL1127.62418.
Google Scholar
3 Zhu W., Nonlinear Stochastic Dynamics and Control in Hamiltonian Formulation, 2003, Science Press, Beijing, China.
Google Scholar
4 Sri Namachchivaya N., Stochastic bifurcation, Applied Mathematics and Computation. (1990) 38, no. 2, 101–159, https://doi.org/10.1016/0096-3003(90)90051-4, MR1059300, ZBL0715.93065.
10.1016/0096-3003(90)90051-4
Web of Science® Google Scholar
5 Khasminskii R. Z., On the principle of averaging the Itô′s stochastic differential equations, Kybernetika. (1968) 4, 260–279, MR0260052.
Google Scholar
6 Keller H., Random Attractors and and bifurcations of the stochastic Lorenz system, Technical Report, 1996, no. 389, Institut für Dynamische Systeme, Universität Bremen.
Google Scholar
7 Huang D., Wang H., Feng J., and Zhu Z.-W., Hopf bifurcation of the stochastic model on HAB nonlinear stochastic dynamics, Chaos, Solitons and Fractals. (2006) 27, no. 4, 1072–1079, https://doi.org/10.1016/j.chaos.2005.04.086, MR2166689, ZBL1134.34312.
10.1016/j.chaos.2005.04.086
Web of Science® Google Scholar
8 Hong L. and Sun J.-Q., Codimension two bifurcations of nonlinear systems driven by fuzzy noise, Physica D: Nonlinear Phenomena. (2006) 213, no. 2, 181–189, https://doi.org/10.1016/j.physd.2005.11.005, MR2201197, ZBL1104.34030.
10.1016/j.physd.2005.11.005
Web of Science® Google Scholar
9 Huang Z., Yang Q., and Cao J., Stochastic stability and bifurcation for the chronic state in Marchuk′s model with noise, Applied Mathematical Modelling. (2011) 35, no. 12, 5842–5855, https://doi.org/10.1016/j.apm.2011.05.027, MR2820955, ZBL1228.93086.
10.1016/j.apm.2011.05.027
Web of Science® Google Scholar
10 Hasegawa H., Stochastic bifurcation in FitzHugh-Nagumo ensembles subjected to additive and/or multiplicative noises, Physica D: Nonlinear Phenomena. (2008) 237, no. 2, 137–155, https://doi.org/10.1016/j.physd.2007.08.009, MR2434099, ZBL1151.34047.
10.1016/j.physd.2007.08.009
Web of Science® Google Scholar
11 Hayase Y., Wehner S., Küppers J., and Brand H. R., External noise imposed on the reaction-diffusion system CO+O₂ → CO₂ on Ir(111) surfaces: experiment and theory, Physical Review E. (2004) 69, no. 2, 15, 2-s2.0-42749100661, https://doi.org/10.1103/PhysRevE.69.021609, 021609.
10.1103/PhysRevE.69.021609
Web of Science® Google Scholar
12 Wehner S., Hoffmann P., Schmeißer D., Brand H. R., and Küppers J., Spatiotemporal patterns of external noise-induced transitions in a bistable reaction-diffusion system: photoelectron emission microscopy experiments and modeling, Physical Review Letters. (2005) 95, no. 3, 1–4, 2-s2.0-27144521084, https://doi.org/10.1103/PhysRevLett.95.038301, 038301.
10.1103/PhysRevLett.95.038301
Web of Science® Google Scholar
13 Hoffmann P., Wehner S., Schmeisser D., Brand H. R., and Küppers J., Noise-induced spatiotemporal patterns in a bistable reaction-diffusion system: photoelectron emission microscopy experiments and modeling of the CO oxidation reaction on Ir(111), Physical Review E. (2006) 73, no. 5, 2-s2.0-33646879005, https://doi.org/10.1103/PhysRevE.73.056123, 056123.
10.1103/PhysRevE.73.056123
CAS PubMed Web of Science® Google Scholar
14 Bodega P. S., Alonso S., and Rotermund H. H., Effects of external global noise on the catalytic CO oxidation on Pt(110), Journal of Chemical Physics. (2009) 130, no. 8, 2-s2.0-61449100602, https://doi.org/10.1063/1.3078037, 084704.
10.1063/1.3078037
CAS PubMed Web of Science® Google Scholar
15 Cisternas J., Escaff D., Descalzi O., and Wehner S., Stochastic model calculation for the carbon monoxide oxidation on iridium(111) surfaces, International Journal of Bifurcation and Chaos. (2009) 19, no. 10, 3461–3472, 2-s2.0-73149112860, https://doi.org/10.1142/S0218127409024906.
10.1142/S0218127409024906
Web of Science® Google Scholar
16 Bär M., Zülicke C., Eiswirth M., and Ertl G., Theoretical modeling of spatiotemporal self-organization in a surface catalyzed reaction exhibiting bistable kinetics, The Journal of Chemical Physics. (1992) 96, no. 11, 8595–8604, 2-s2.0-0001382342.
10.1063/1.462312
Web of Science® Google Scholar
17 Wehner S., Baumann F., and Küppers J., Kinetic hysteresis in the CO oxidation reaction on Ir(111) surfaces, Chemical Physics Letters. (2003) 370, no. 1-2, 126–131, 2-s2.0-0037423766, https://doi.org/10.1016/S0009-2614(03)00059-9.
10.1016/S0009-2614(03)00059-9
CAS Web of Science® Google Scholar
18 Wehner S., Baumann F., Ruckdeschel M., and Küppers J., Kinetic phase transitions in the reaction CO+O→CO₂ on Ir(111) surfaces, Journal of Chemical Physics. (2003) 119, no. 13, 6823–6831, 2-s2.0-0142052904, https://doi.org/10.1063/1.1603212.
10.1063/1.1603212
CAS Web of Science® Google Scholar
19 Hale J., Theory of Functional Differential Equations, 1977, Springer, New York, NY, USA, MR0508721.
10.1007/978-1-4612-9892-2
Web of Science® Google Scholar
20 Hale J. K. and Verduyn Lunel S. M., Introduction to Functional-Differential Equations, 1993, 99, Springer, New York, NY, USA, MR1243878.
10.1007/978-1-4612-4342-7
Google Scholar
21 Fofana M. S., Aspects of stable and unstable machining by Hopf bifurcation, Applied Mathematical Modelling. (2002) 26, no. 10, 953–973, 2-s2.0-0041947254, https://doi.org/10.1016/S0307-904X(02)00052-5.
10.1016/S0307-904X(02)00052-5
Web of Science® Google Scholar
22 Guckenheimer J. and Holmes P., Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields, 1983, 42, Springer, New York, NY, USA, MR709768.
10.1007/978-1-4612-1140-2
Google Scholar
23 Hassard B. D., Kazarinoff N. D., and Wan Y. H., Theory and Applications of Hopf Bifurcation, 1981, 41, Cambridge University Press, Cambridge, UK, London Mathematical Society Lecture Note Series, MR603442.
Google Scholar
24 Campbell S. A., Bélair J., Ohira T., and Milton J., Limit cycles, tori, and complex dynamics in a second-order differential equation with delayed negative feedback, Journal of Dynamics and Differential Equations. (1995) 7, no. 1, 213–236, https://doi.org/10.1007/BF02218819, MR1321711, ZBL0816.34048.
10.1007/BF02218819
Google Scholar

All articles

Deterministic and Stochastic Bifurcations of the Catalytic CO Oxidation on Ir(111) Surfaces with Multiple Delays

Abstract

1. Introduction

2. Deterministic System

2.1. The Single Hopf Bifurcation

2.2. The Double Hopf Bifurcation

3. Stochastic System

3.1. Stochastic D-Bifurcation

3.2. P-Bifurcation

4. Conclusion

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Deterministic and Stochastic Bifurcations of the Catalytic CO Oxidation on Ir(111) Surfaces with Multiple Delays

Abstract

1. Introduction

2. Deterministic System

2.1. The Single Hopf Bifurcation

2.2. The Double Hopf Bifurcation

3. Stochastic System

3.1. Stochastic D-Bifurcation

3.2. P-Bifurcation

4. Conclusion

Acknowledgments

References

Figures

References

Related

Information