An efficient solution algorithm for sinc-Galerkin method has been presented for obtaining numerical solution of PDEs with Dirichlet-type boundary conditions by using Maple Computer Algebra System. The method is based on Whittaker cardinal function and uses approximating basis functions and their appropriate derivatives. In this work, PDEs have been converted to algebraic equation systems with new accurate explicit approximations of inner products without the need to calculate any numeric integrals. The solution of this system of algebraic equations has been reduced to the solution of a matrix equation system via Maple. The accuracy of the solutions has been compared with the exact solutions of the test problem. Computational results indicate that the technique presented in this study is valid for linear partial differential equations with various types of boundary conditions.

1. Introduction

Sinc methods for differential equations were originally introduced by Stenger in [1–3]. The sinc functions were first analyzed in [4, 5] and a detailed research of the method for two-point boundary-value problems can be found in [6, 7]. In [8], parabolic and hyperbolic problems are presented in detail. To solve a problem arising from chemical reactor theory, the properties of the sinc-Galerkin method are used to reduce the computation of nonlinear two-point boundary-value problems to some algebraic equations in [9]. A computer algorithm for sinc method to solve numerically the linear and nonlinear ODEs and their simulations has been presented in [7, 10], respectively. The full sinc-Galerkin method is developed for a family of complex-valued partial differential equations with time-dependent boundary conditions [9]. A study of the performance of the Galerkin method using sinc basis functions for solving Bratu’s problem is presented in [11]. In [12] a numerical algorithm has been presented for recovering the unknown function and obtaining a solution to the inverse ill-posed problem. They have presented a Galerkin method with the sinc basis functions in both space and time domains for solving the direct problem. A sinc-collocation method has been developed for solving linear systems of integrodifferential equations of Fredholm and Volterra type with homogeneous boundary conditions in [13].

2. Sinc-Approximation Formula for PDEs

We use the sinc-Galerkin method as mentioned in [1] to derive an approximate solution of the following:

()

For the equation given above, the sinc-Galerkin scheme can be developed in both space and time directions as follows.

In general, approximations can be constructed for infinite, semi-infinite, and infinite intervals and both spatial and time spaces will be introduced. Define the function

()

which is a conformal mapping from D_E, the eye-shaped domain in the z-plane, onto the infinite strip, D_S, where

()

A more general form of sinc basis according to intervals can be given as follows:

()

where

()

and the conformal maps for both directions

()

are used to define the basis functions on the intervals (0, l) and (0, ∞), respectively. h_x, h_t > 0 represents the mesh sizes in the space direction and the time direction, respectively. The sinc nodes x_i and t_j are chosen so that x_i = ϕ⁻¹(ih_x), t_j = γ⁻¹(jh_t).

Here the function x = ϕ⁻¹(x) = e^x/(1 + e^x) is an inverse mapping of ϕ = ϕ(x). We may define the range of ϕ⁻¹ on the real line as

()

For the evenly spaced nodes

on the real line, the image which corresponds to these nodes is denoted by

()

where 0 < x_k < 1, for all k.

The sinc basis functions in (4) do not have a derivative when x tends to 0 or 1. We modify the sinc basis functions as

()

where

()

For the temporal space, we construct an approximation by defining the function

()

which is a conformal mapping from D_W, the wedge-shaped domain in the r-plane, onto the infinite strip, D_S, where

()

derived from composite translated functions

()

for r ∈ D_W.

Here w = γ(r) and γ⁻¹(w) = r = e^w. We may define γ⁻¹ on the real line as

()

For the evenly spaced nodes

on the real line, the image which corresponds to these nodes is denoted by

()

where 0 < t_k < ∞, for all k.

A list of conformal mappings may be found in Table 1 [14].

Table 1. Conformal mappings and nodes for several subintervals of R.

(a, b)		ϕ (z)	z_k
a	b
0	1
0	∞	ln(z)	e^kh
0	∞	ln(sinh(z))
−∞	∞	z	kh
−∞	∞	sinh⁻¹(z)	kh

Definition 1. Let B(D_E) be the class of functions F that are analytic in D_E and satisfy

()

where

()

and on the boundary of D_E satisfy

()

The proof of the following theorems can be found in [1].

Theorem 2. Let Γ be (0,1), F ∈ B(D_E), and then for h > 0 sufficiently small

()

where

()

For the sinc-Galerkin method, the infinite quadrature rule must be truncated to a finite sum; the following theorem indicates the conditions under which exponential convergence results.

Theorem 3. If there exist positive constants α, β, and C such that

()

then the error bound for the quadrature rule (19) is

()

The infinite sum in (19) is truncated with the use of (20) to arrive at (22).

Making the selections

()

where ∥·∥ is integer part of statement,

()

Theorems 2 and 3 can be used to approximate the integrals that arise in the formulation of the discrete systems corresponding to two-point BVPs.

3. Discrete Solutions Scheme for Two-Point BVPs

In ordinary differential equations

()

on Γ₁, sinc solution is assumed as an approximate solution u_m in the form of series with m = 2N + 1 terms

()

The coefficients

are determined by orthogonalizing the residual Lu − f with respect to the sinc basis functions

where S_k(z) = S(k, h)∘ϕ(z). An inner product for two continuous functions such as f₁ and f₂ can be given by the following formula

()

where w is the weight function and is chosen depending on boundary conditions. If we implement the above inner product rule in orthogonalization, this yields the discrete sinc-Galerkin system:

()

Now, we are going to derive discrete sinc-Galerkin system for PDEs. Assume

is the approximate solution of (1).Then, the discrete system takes the following form:

()

The coefficients

are determined by orthogonalizing the residual

with respect to the sinc basis functions

where S_jS_h(z, t) = S(j, h)∘ϕ(z)S(k, h)∘γ(t) for −N ≤ j, k ≤ N. In this case the inner product takes the following form:

()

The choice of the weight function w(z, t) in the double integrand depends on the boundary conditions, the domain, and the partial differential equation. Therefore, the discrete Galerkin system is

()

4. Matrix Representation of the Derivatives of Sinc Basis Functions at Nodal Points

The sinc-Galerkin method actually requires the evaluated derivatives of sinc basis functions at the sinc nodes, z = z_j. The rth derivative of S_k(z) = S(k, h)∘ϕ(z) with respect to ϕ, evaluated at the nodal point z_j, is denoted by

()

The expressions in (14) for each p and j can be stored in a matrix

. For r = 0,1, 2, …

()

where

()

The chain rule has been used for the z-derivative of product sinc functions. For example, when S_k(z) = S(k, h)∘ϕ(z),

()

Now, we are going to develop discrete form for (1). We choose for special case the parameters as follows for the spatial dimension:

()

and for the temporal space as

()

The discrete form of (1) can be given the following form:

()

We solve this by taking our approximating basis functions to be

()

If we apply sinc-quadrature rules with the help of (32)–(37) on the definite integral given (38) by using (39), we can get the following matrix system.

Let A_m(u) denote a diagonal matrix, whose diagonal elements are u(x_−N), u(x_−N+1), …, u(x_N) and nondiagonal elements are zero. Then (38) reproduces the following matrixes accordingly.

Firstly we set the coefficient matrix as follows:

()

Finally, for the right side function F given (1) can be written in the following matrix form:

()

Using (32)–(37) we arrive at a matrix system given in [1] as follows:

()

Finally, by using Maple Computer Algebra Software, the matrix system (42) can be solved by using LU or QR decomposition method and unknown coefficients can be found. After calculation of C we get approximate solution as follows:

()

5. Numerical Simulation

The example in this section will illustrate the sinc method.

Example 4. This problem has been addressed in [1]. The following equation is given in Dirichlet-type boundary condition:

()

The particular solution of (44) can be calculated via separation variables rules and can be given as follows:

()

For (44) we choose sinc components here in the following:

()

According to the above parameters, the approximate solution simulation of (44) has been given in Figure 1 and numerical results also can be found in Table 2.

Table 2. Numerical results.

	t	Exact solution	Sinc-Galerkin solution	Error
N = 16, x = 0.6	0.1	0.35446621870000	0.59102026517764600	0.23655404647764600
	0.11	0.00001833412226	−0.08327827240548060	0.08329660652774060
	0.21	0.9482992112 × 10⁻⁹	−0.03068110846399060	0.03068110941228980
	0.31	0.4904905672 × 10⁻¹³	−0.01083286679129120	0.01083286679134030
	0.41	0.2536973471 × 10⁻¹⁷	−0.000420168677914081	0.000420168677914083
	0.51	0.1312203514 × 10⁻²¹	−0.00108069489771883	0.00108069489771883
	0.61	0.6787134677 × 10⁻²⁶	−0.00492511086695295	0.00492511086695295
	0.71	0.3510522275 × 10⁻³⁰	0.00331706758955819	0.00331706758955819
	0.81	0.1815753976 × 10³⁴	−0.00303031084399243	0.00303031084399243
	0.91	0.9391658013 × 10⁻³⁹	0.00342519240062265	0.00342519240062265

Details are in the caption following the image — **Figure 1 (a) The sinc-Galerkin solutions according to the grid points size N**
Open in figure viewer PowerPoint

Simulation of approximate solution.

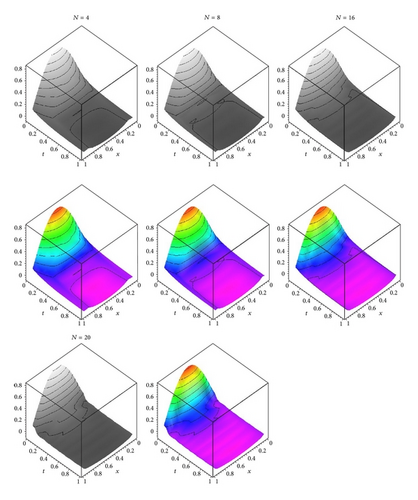
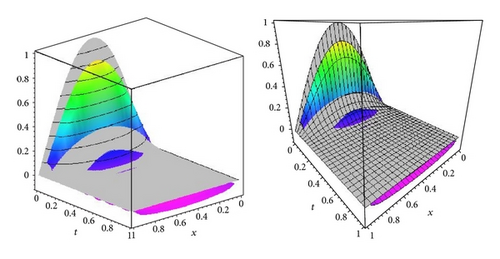
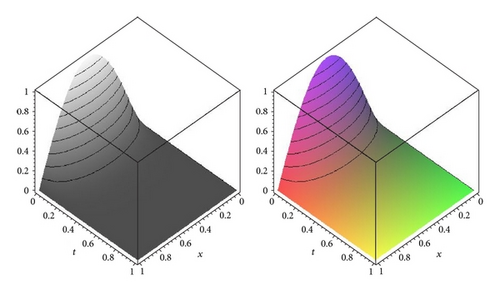
6. Conclusions

We have developed a Maple algorithm to solve and simulate second-order parabolic PDEs with Dirichlet-type boundary conditions based on sinc-Galerkin approximation on some closed real intervals and the method has been compared with the exact solutions. When compared with other computational approaches, this method turns out to be more efficient in the sense that selection parameters and changing boundary conditions and also giving different problems to the algorithms. The accuracy of the solutions improves by increasing the number of sinc grid points N. The method presented here is simple and uses sinc-Galerkin method that gives a numerical solution, which is valid for various boundary conditions. Several PDEs have been solved by using our technique in less than 20 seconds. All computations and graphical representations have been prepared automatically by our algorithm.

Conflict of Interests

The author declares that he has no conflict of interests.

Appendix

See Algorithm 1.

Algorithm 1

restart:
with(linalg):
with(LinearAlgebra):
N:=16:
d:=Pi/2:
h:=0.75/sqrt(N);
s:=.5/sqrt(N);
SIZE:=2*N+1;
delta0:=(i,j)->piecewise(j=i,1,j<>i,0):
delta1:=(i,j)->piecewise(i=j,0,i<>j,((-1) ^∧(i-j))/(i-j)):
delta2:=(i,j)->piecewise(i=j,(-Pi ^∧2)/3,i<>j,-2*(-1) ^∧(i-j)/(i-j) ^∧2):
I_0:=Matrix(SIZE,delta0):
I_1:=Matrix(SIZE,delta1):
I_2:=Matrix(SIZE,delta2):
xk:=1/2+1/2*tanh(k*h/2);
xk_func:=unapply(xk,k);
phi:=unapply(log((x)/(1-x)),x);
Dphi:=unapply(simplify(diff(phi(x),x)),x);
g:=unapply(simplify(1/diff(phi(x),x)),x);
Dg:=unapply(diff(g(x),x),x);
gk:=unapply(subs(x=xk,g(x)),k);
Dgk:=unapply(subs(x=xk,Dg(x)),k);
g_Div_Dphi:=unapply(g(x)/Dphi(x),x);
g_Div_Dphi_k:=unapply(subs(x=xk,g_Div_Dphi(x)),k);
#Temporal Spaces;
tl:=exp(l*s);
tl_func:=unapply(tl,l);
gamm:=unapply(log(t),t);
Dgam:=unapply(diff(gamm(t),t),t);
g_gamm:=unapply(1/diff(gamm(t),t),t);
g_gamm_l:=unapply(subs(t=tl,g_gamm(t)),l);
gamm_Div_Dgam:=unapply(g_gamm(t)/Dgam(t),t);
gamm_Div_Dgam:= t-> t ^∧2;
gamm_Div_Dgam_l:=unapply(subs(t=tl,gamm_Div_Dgam(t)),l);
GenerateDiagonalAm := proc( x )
local i:=1:
local A:=Matrix(SIZE):
for i from 1 by 1 to SIZE
do
A[i,i]:=evalf(x(-N+i-1)):
end do:
return A;
end proc;
B:= -2*h*MatrixMatrixMultiply(I_0,GenerateDiagonalAm(gk))+
MatrixMatrixMultiply(I_1,GenerateDiagonalAm(Dgk))+1/h*I_2:
DD:=h*GenerateDiagonalAm(g_Div_Dphi_k):
C:=MatrixMatrixMultiply(GenerateDiagonalAm(g_gamm_l),s*(I_0-I_1)):
E:=s*GenerateDiagonalAm(gamm_Div_Dgam_l):
Fkl:=unapply((Pi ^∧2-4)*sin(Pi*xk_func(k-N-1))*exp(-tl_func(l-N-1)),k,l);
F:=evalf(Matrix(SIZE,Fkl)):
V:=Matrix(SIZE,v):
EQN_SYS:=evalf(
MatrixMatrixMultiply(
MatrixMatrixMultiply(
Matrix(inverse(DD)),B
),V
)
)
+evalf(
MatrixMatrixMultiply(
MatrixMatrixMultiply(
V,C),Matrix(inverse(E)
)
)
):
SYS:=[]:
for i from 1 by 1 to SIZE
do
for j from 1 by 1 to SIZE
do
SYS:=[op(SYS),EQN_SYS(i,j)=F(i,j)];
end do:
end do:
vars:=seq(seq(v(i,j),i=1..2*N+1),j=1..2*N+1):
A,b:LinearAlgebra[GenerateMatrix](evalf(SYS),[vars]):
c:=linsolve(A,b):
CoeffMatrix=Matrix(SIZE):
cnt:=1;
for i to SIZE do
for j to SIZE do
CoeffMatrix[j,i]:=c[cnt]:
cnt:=cnt+1
end do;
end do;
CoeffMatrix:=Matrix(CoeffMatrix,SIZE):
ApproximateSol:=unapply(
evalf(
sum(
sum("CoeffMatrix"[m+N+1,n+N+1]
*sin(Pi*(phi(x)-m*h)/h)/(Pi*(phi(x)-m*h)/h)
*sin(Pi*(gamm(t)-n*s)/s)/(Pi*(gamm(t)-n*s)/s)
,m=-N..N),
n=-N…N)
)
+exp(-4*t)*sin(Pi*x)
,x,t):
plot3d(ApproximateSol(x,t),x=0..1,t=0..1):
Exact:=unapply(exp(-Pi ^∧2*t)*sin(Pi*x),x,t);
plot3d(Exact(x,t),x=0..1,t=0..1);
plot3d({Exact(x,t),ApproximateSol(x,t)},x=0..1,t=0..1);
XX:=.6;
#Numerical Comparision EXACT
for j from 0.1 to 10 by 1
do
evalf(Exact(XX,j)):
od;
#Numerical Comparision APPROX
for j from 0.1 to 10 by 1
do
evalf(ApproximateSol(XX,j)):
od;
#Numerical Comparision ERROR
for j from 0.1 to 10 by 1
do
abs(evalf(evalf(ApproximateSol(XX,j)-Exact(XX,j)))):
od;

References

1 Stenger F., A Sinc-Galerkin method of solution of boundary value problems, Mathematics of Computation. (1979) 33, no. 145, 85–109, https://doi.org/10.2307/2006029, MR514812, ZBL0402.65053.
10.2307/2006029
Web of Science® Google Scholar
2 Stenger F., Summary of Sinc numerical methods, Journal of Computational and Applied Mathematics. (2000) 121, no. 1-2, 379–420, https://doi.org/10.1016/S0377-0427(00)00348-4, MR1780056, ZBL0964.65010.
10.1016/S0377-0427(00)00348-4
Web of Science® Google Scholar
3 Stenger F., Approximations via Whittaker′s cardinal function, Journal of Approximation Theory. (1976) 17, no. 3, 222–240, MR0481786, https://doi.org/10.1016/0021-9045(76)90086-1, ZBL0332.41013.
10.1016/0021-9045(76)90086-1
Web of Science® Google Scholar
4 Whittaker E. T., On the functions which are represented by the expansions of the interpolation theory, Proceedings of the Royal Society of Edinburg. (1915) 35, 181–194.
10.1017/S0370164600017806
Google Scholar
5 Whittaker J. M., Interpolation Function Theory, Cambridge Tracts in Mathematics and Mathematical Physics, 1935, no. no. 33, Cambridge University Press, London, UK, by E. F. Beckenbach, McGraw-Hill, New York, NY, USA, 1961.
Google Scholar
6 Lund J., Symmetrization of the sinc-Galerkin method for boundary value problems, Mathematics of Computation. (1986) 47, no. 176, 571–588, https://doi.org/10.2307/2008173, MR856703, ZBL0629.65085.
10.1090/S0025-5718-1986-0856703-9
Web of Science® Google Scholar
7 Secer A. and Kurulay M., The Sinc-Galerkin method and its applications on singular Dirichlet-type boundary value problems, Boundary Value Problems. (2012) 2012, article 126, https://doi.org/10.1186/1687-2770-2012-126, MR3017158.
10.1186/1687?2770?2012?126
Google Scholar
8 McArthur K. M., Bowers K. L., and Lund J., Numerical implementation of the Sinc-Galerkin method for second-order hyperbolic equations, Numerical Methods for Partial Differential Equations. (1987) 3, no. 3, 169–185, https://doi.org/10.1002/num.1690030303, MR1012912, ZBL0698.65069.
10.1002/num.1690030303
Google Scholar
9 Saadatmandi A., Razzaghi M., and Dehghan M., Sinc-Galerkin solution for nonlinear two-point boundary value problems with applications to chemical reactor theory, Mathematical and Computer Modelling. (2005) 42, no. 11-12, 1237–1244, 2-s2.0-28844464738, https://doi.org/10.1016/j.mcm.2005.04.008, ZBL1085.65065.
10.1016/j.mcm.2005.04.008
Web of Science® Google Scholar
10 Secer A., Kurulay M., Bayram M., and Akinlar M. A., An efficient computer application of the Sinc-Galerkin approximation for nonlinear boundary value problems, Boundary Value Problems. (2012) 2012, article 117, https://doi.org/10.1186/1687-2770-2012-117, MR3017156.
10.1186/1687?2770?2012?117
Google Scholar
11 Rashidinia J., Maleknejad K., and Taheri N., Sinc-Galerkin method for numerical solution of the Bratu′s problems, Numerical Algorithms. (2013) 62, no. 1, 1–11, https://doi.org/10.1007/s11075-012-9560-3, MR3009552, ZBL1259.65126.
10.1007/s11075-012-9560-3
Web of Science® Google Scholar
12 Shidfar A. and Babaei A., The sinc-Galerkin method for solving an inverse parabolic problem with unknown source term, Numerical Methods for Partial Differential Equations. (2013) 29, no. 1, 64–78, https://doi.org/10.1002/num.21699, MR3003101, ZBL1255.65171.
10.1002/num.21699
Web of Science® Google Scholar
13 Zarebnia M. and Abadi M. G. A., A numerical sinc method for systems of integro-differential equations, Physica Scripta. (2010) 82, no. 5, 2-s2.0-78149371454, https://doi.org/10.1088/0031-8949/82/05/055011, 055011, ZBL1205.65343.
10.1088/0031-8949/82/05/055011
Web of Science® Google Scholar
14 Lund J. and Bowers K. L., Sinc Methods for Quadrature and Differential Equations, 1992, SIAM, Philadelphia, Pa, USA, https://doi.org/10.1137/1.9781611971637, MR1171217.
10.1137/1.9781611971637
Google Scholar

All articles

Numerical Solution and Simulation of Second-Order Parabolic PDEs with Sinc-Galerkin Method Using Maple

Abstract

1. Introduction

2. Sinc-Approximation Formula for PDEs

3. Discrete Solutions Scheme for Two-Point BVPs

4. Matrix Representation of the Derivatives of Sinc Basis Functions at Nodal Points

5. Numerical Simulation

6. Conclusions

Conflict of Interests

Appendix

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Numerical Solution and Simulation of Second-Order Parabolic PDEs with Sinc-Galerkin Method Using Maple

Abstract

1. Introduction

2. Sinc-Approximation Formula for PDEs

3. Discrete Solutions Scheme for Two-Point BVPs

4. Matrix Representation of the Derivatives of Sinc Basis Functions at Nodal Points

5. Numerical Simulation

6. Conclusions

Conflict of Interests

Appendix

References

Figures

References

Related

Information