Buoyancy Effect of Ionic Vacancy on the Change of the Partial Molar Volume in Ferricyanide-Ferrocyanide Redox Reaction under a Vertical Gravity Field
Abstract
With a gravity electrode (GE) in a vertical gravity field, the buoyancy effect of ionic vacancy on the change of the partial molar volume in the redox reaction between ferricyanide (FERRI) and ferrocyanide (FERRO) ions was examined. The buoyancy force of ionic vacancy takes a positive or negative value, depending on whether the rate-determining step is the production or extinction of the vacancy. Though the upward convection over an upward electrode in the FERRO ion oxidation suggests the contribution of the positive buoyancy force arising from the vacancy production, the partial molar volume of the vacancy was not measured. On the other hand, for the downward convection under a downward electrode in the FERRI ion reduction, it was not completely but partly measured by the contribution of the negative buoyancy force from the vacancy extinction. Since the lifetime of the vacancy is decreased by the collision between ionic vacancies during the convection, the former result was ascribed to the shortened lifetime due to the increasing collision efficiency in the enhanced upward convection over an upward electrode, whereas the latter was thought to arise from the elongated lifetime due to the decreasing collision efficiency by the stagnation under the downward electrode.
1. Introduction
In electrochemistry, the density change in the solution during an electrode reaction gives rise to a gravitational convection [1]. Constant currents observed for hanging electrodes often come from the steady-state mass transfer by the gravitational convection under a parallel gravity field. As a force similar to gravitational force, centrifugal force often affects ionic transportation processes, for example, leading to thermodynamic emf generation [2] and bringing about hydrodynamic convection.
Gravity electrode (GE) is, as shown in Figure 1, operated in a high gravity field arising from a centrifugal force, which provides a great buoyancy force in the solution, promoting a gravitational convection. As shown in the theoretical analysis in Appendix, it was clarified that the buoyancy force comes from the change in the partial molar volume between product and reactant ions [3]. First, the effective density coefficient in the limiting diffusion (γ)lim in an electrode reaction is measured. Then, from (A.33) in Appendix, the change in the partial molar volume ΔVG is calculated. On the other hand, in (A.30a) in Appendix, ΔVG is defined by the partial molar volumes of the product ion VP and reactant ion VR in the form of . Reflecting the measurement of the diffusion current, is expressed by zRDR/(zPDP) in (A.30c) in Appendix, where zR and zP are the electron numbers without signs transferring between the reactant and product in the reaction, respectively. DR and DP are the diffusion coefficients of the reactant and product, respectively. Therefore, if VP and VR are consistent with the equilibrium values, and measured by pycnometer (PM) mentioned later, the calculated value will agree with ΔVG. This is the blank test for the validity of the GE method. FERRO ion oxidation was actually performed, so that it was concluded that the data obtained by this method do not contain any other extra partial molar volumes and agree with thermodynamic data [4].
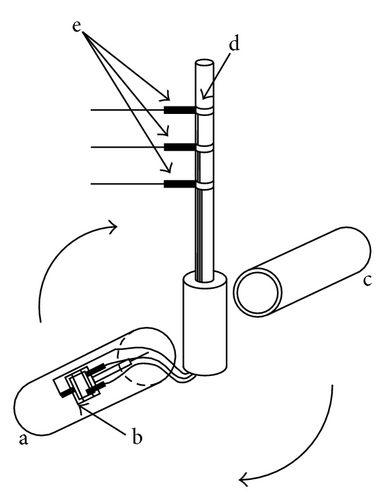
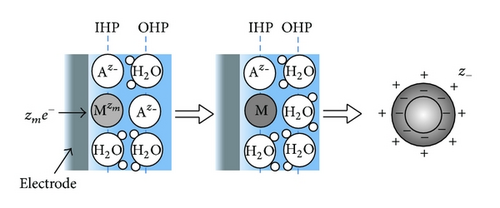
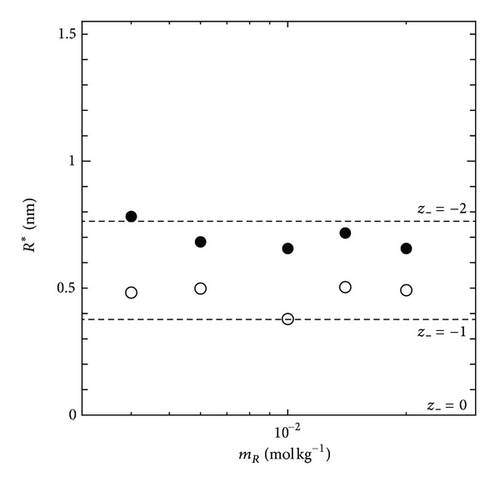
On the other hand, by using the GE method, as an extra component, the partial molar volume of ionic vacancy has been newly measured in copper electrodeposition [5, 6]. Figure 2 represents a schematic figure of the ionic vacancy; the center of an ionic vacancy is a charged vacuum void surrounded by an ionic cloud, and it has a size of the order of 0.1 nm. In Figure 3, it is shown that the measured radii of ionic vacancies agree well with the theoretical values. As shown in Figure 3, the vacancies created in cupric sulfate and cupric chloride solutions have −2 and −1 unit charges, respectively.

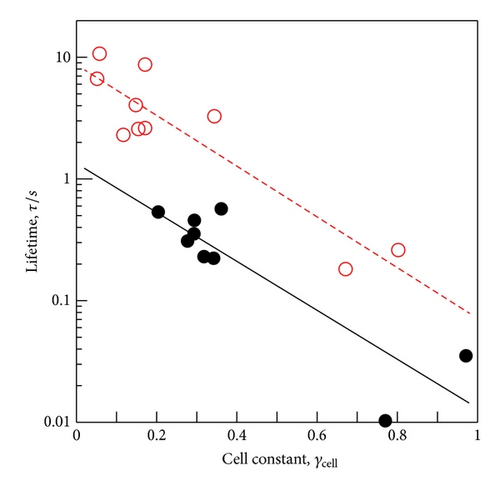
Recently, with a new electrode system called cyclotron magnetohydrodynamic (MHD) electrode (cyclotron MHDE), the lifetimes of ionic vacancies in some reactions have been measured, where the electrolyte solution together with ionic vacancies circulated along a pair of concentric cylinder electrodes in a vertical magnetic field [7]. The lifetime was measured from the circulating velocity. As a characteristic feature, the lifetime decreased with an increasing collision efficiency of ionic vacancies; copper depositions in magnetic fields from 1 T to 18 T lead to the vacancy lifetimes varying from 10 s to 0.1 s [7]. Though 10 times smaller than in the case of copper deposition, that is, 1 s to 0.01 s, in FERRI-FERRO redox reaction, the lifetime of ionic vacancy was also measured [8]. From these results, it was thought that there are two processes to determine the lifetime of ionic vacancy; one is the decay to the initial state, and the other is the conversion to nanobubble [7]. Here, nanobubble is the smallest type of bubble containing a gas. Recently, the formation process from ionic vacancies has been theoretically clarified [6]. Actually, in Figure 4, the plots of the lifetime τ against the cell constant γcell in copper deposition and FERRI-FERRO reaction are represented [7, 8], where γcell implies the collision efficiency of ionic vacancy [7]. For γcell = 0, the lifetime thus corresponds to the decay rate of ionic vacancy without collision, whereas for γcell = 1, it implies the formation time of nanobubble by collision of each vacancy. As will be discussed in the following, these experimental data elucidate the reason why by means of the GE method, ionic vacancy was observed in copper deposition, but not in FERRO ion oxidation; that is, the lifetimes in FERRO ion oxidation are too short to measure by the GE method. Since the time scale of the convection in GE is estimated of the order of 1 s or so, the GE method has the upper limit of the same order for the measurement.
In the present paper, in view of the lubricant effect of ionic vacancy, the convective-diffusion process in a vertical gravity field is first reexamined. Then, the change of the partial molar volume including ionic vacancy in a redox reaction is theoretically derived. Finally, the buoyancy effect of ionic vacancy in the redox reactions between FERRI and FERRO ions is experimentally examined.
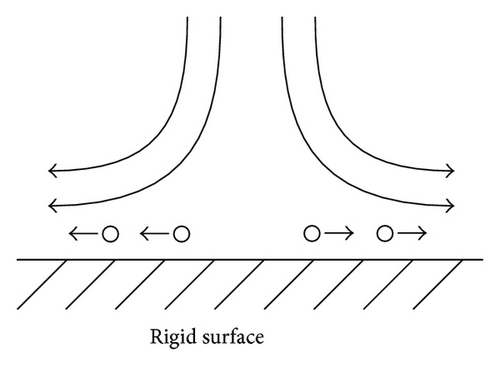
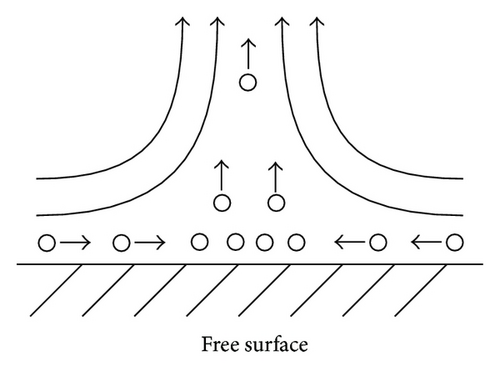
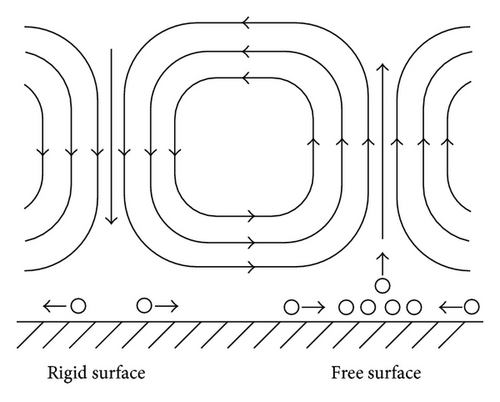
2. Theoretical
2.1. Diffusion Current Equation including the Lubricant Effect of Ionic Vacancy
In the analysis of the chirality appearing in electrodeposition under a vertical magnetic field [10, 11], it has been clarified that ionic vacancy plays an important role of a lubricant [9, 12]. This is because ionic vacancy is easy to coalesce at electrode surface, so that the friction between the solution and the electrode is greatly decreased. As a result, two different kinds of surfaces emerge on an electrode surface, that is, surfaces covered without and with ionic vacancies, which are classified as rigid and free surfaces with and without friction, respectively. In the previous analysis of the convective-diffusion current under a high gravity field, however, we considered only a conventional rigid surface without ionic vacancies [13]. Figure 5 exhibits the formation processes of the free and rigid surfaces by ionic vacancies on an upward electrode; under the upward flow, following the stream lines, ionic vacancies are gathered to the center, covering the surface, whereas under the downward flow, they are swept away from the center, exposing the bare surface. Namely, the free and rigid surfaces arise from upward and downward flows, respectively. In Figure 6, a set of convection flows formed on the free and rigid surfaces is exhibited; the flow ascending from the free surface with ionic vacancies descends to the rigid surface without them. As discussed elsewhere [13], the convection in a vertical gravity field takes place between the electrode surface and the outer boundary of the convective-diffusion layer. Since the outer boundary provides the free surface, as shown in Figure 7, for the rigid electrode surface without ionic vacancies, the boundary conditions of the convection are consistent with those of rigid and free boundaries (Figure 7(a)), whereas for the free electrode surface completely covered with ionic vacancies, the conditions are given by two free boundaries (Figure 7(b)).
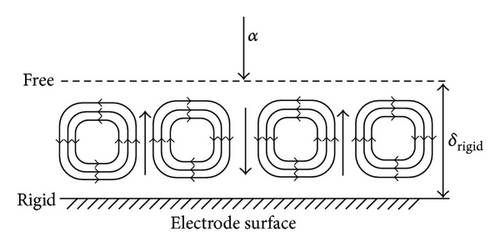
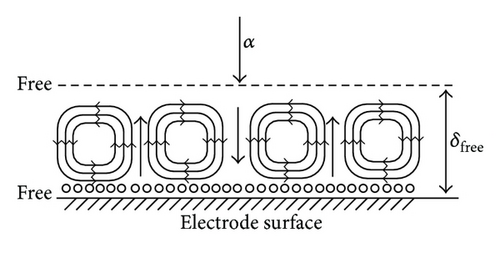
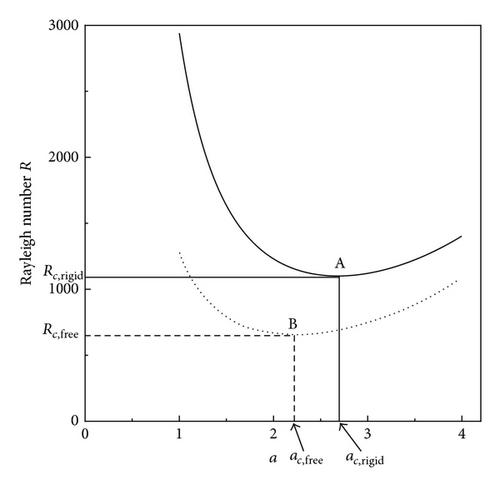
In accordance with the way in the previous paper [3], the Rayleigh numbers corresponding to the two kinds of mathematical solutions for the convection on rigid and free electrode surfaces are separately calculated against the nondimensional wave number of the convection flow. Figure 8 represents the result of the calculation; the critical Rayleigh number corresponding to the rigid electrode surface Rc,rigid = 1100.7 for the critical dimensionless wave number ac,rigid = 2.68 is larger than that to the free electrode surface Rc,free = 657.51 for ac,free = 2.221, so that under the condition R = Rc,free, the convection cells are possible for the upward flows on the free surface but are impossible for the downward flow on the rigid surface, that is, the convection cells shown in Figure 6 are as a whole not completed. To compensate this insufficient condition, it is necessary that the R increases up to the Rc,rigid for the downward flow to start, which takes the same value of δ as that of the preceding case of a rigid electrode surface [13], so that it is concluded that the diffusion current density equation obtained is consistent with the previous one.
2.2. Rate-Determining Process of the Convection
In FERRO ion oxidation, as mentioned above, ionic vacancy has not been detected by GE. However, as shown in Figure 4, in the redox reactions including the same reaction, the lifetime of ionic vacancy has been measured. In the FERRI-FERRO redox reaction, as will be shown in Figures 11 and 12, the change in the partial molar volume between the product ion and the reactant ion is of the order of 10−5 m3 mol−1, whereas the estimated partial molar volume of ionic vacancy is of the order of 10−4 m3 mol−1. Therefore, if the lifetime was sufficiently long, GE could detect the partial molar volume of the ionic vacancy. However, in Figure 4, the lifetime measurement by the cyclotron MHDE suggests that the increasing flow velocity promotes the collision between ionic vacancies [7], assisting the rapid conversion to nanobubbles, which, due to much larger buoyancy forces, quickly escape from the electrode surface. If the buoyancy force of ionic vacancy enhances the convection, the lifetime will thus become shorter than that in a stationary solution. In the FERRI-FERRO redox reaction, as shown in Figure 4, the lifetime in the case of perfect collision is about 0.01 s, which is only 1/100th of the intrinsic lifetime.
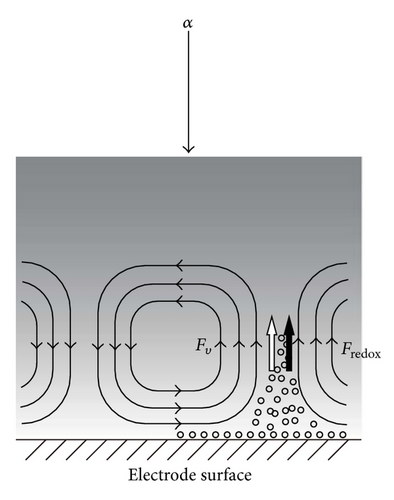
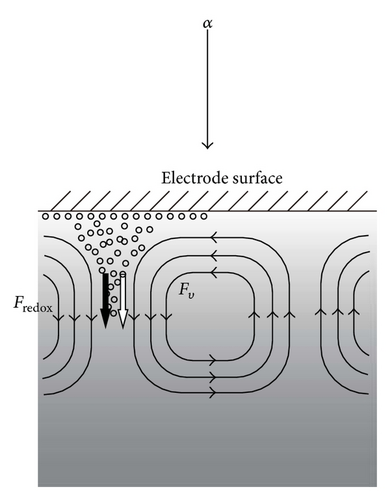
Based on these discussions, in Figures 9(a) and 9(b), we can elucidate the different contributions of ionic vacancies to the convections on upward and downward electrodes; for the FERRO ion oxidation, due to upward convection, as shown in Figure 9(a), the upward electrode is used as the working electrode. The vacancy production with upward buoyancy force thus accelerates the convection, promoting the collision between ionic vacancies, which decreases the lifetime, at most, down to 0.01 s. This is the reason why the vacancy is not detected in the FERRO ion oxidation by the GE method. As have been discussed in Section 1, since the GE method requires the measurement time more than 1 s, it is too short to measure the lifetime. In the case of FERRI ion reduction, due to downward convection, as shown in Figure 9(b), the downward electrode is used. The production of ionic vacancy with upward buoyancy force thus decelerates the convection, forming a stagnation area under the downward electrode; the created vacancies with upward buoyancy forces are first accumulated at the stagnation area, lightening the upper part of the solution, which results in the suppression of the convection. The extinction of the ionic vacancies then gradually takes place, inducing the downward convection with an increasing density. Such extinction process may proceed in a rate of the intrinsic lifetime, that is, 1 s, which is much longer than that of FERRI ion reduction.
2.3. Measurement of the Buoyancy Effect of Ionic Vacancy
3. Experimental
3.1. GE Method
As test reactions, redox reactions between FERRO and FERRI ions were adopted. Concerning FERRO and FERRI ions, each of eighteen samples of 100 mol m−3 K2SO4 solutions was prepared for the molar concentration from 10 mol m−3 to 30 mol m−3. For the measurement of the density coefficient (γ)lim in a limiting-diffusion current, a GE (GE01, Nikko Keisoku Co.) was used in the vertical gravity mode. As shown in Figures 10(a) and 10(b), a pair of circular Pt plates with 5 mm diameter shielded by o-rings was used for working and counter electrodes, where the active areas inside the o-rings were 3.14 mm2. Since the oxidation of FERRO ion decreases the solution density, the upward electrode configuration brings hydrodynamic instability, whereas the reduction of FERRI ion increases the solution density, so that the convection is expected for a downward electrode. Therefore, the upward electrode was used as the working electrode for the oxidation of FERRO ion, and the downward electrode was used as the working electrode for the reduction of FERRI ion. As the reference electrode, a silver wire coated by AgCl film with a 1 mm diameter was used. The reactions were performed at overpotentials of +200 mV and −200 mV for the oxidation and reduction, respectively, that is, at the limiting diffusion ranges. Prior to the measurement, argon bubbling was performed to evacuate dissolve oxygen in the solution. To calculate the constant Av in (7b), the kinematic viscosity ν was measured by the Cannon-Fenske viscometer (Sibata Scientific Technology Ltd.), and the diffusion coefficients DP and DR were determined by the rotating disk electrode (RRDE-1, Nikko Keisoku Co.). The solution was also kept at 27 ± 1°C. After the measurement, according to the procedure elucidated in the preceding paper [4], the data obtained were calculated.
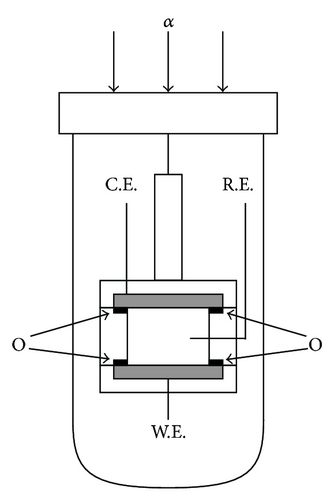
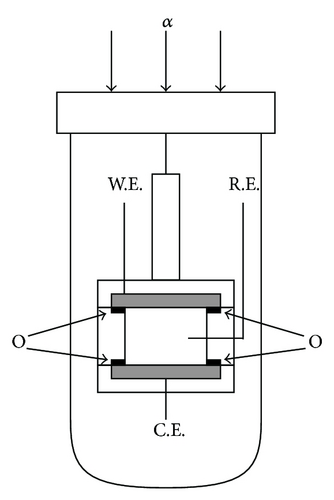
3.2. PM Method
Concerning FERRO and FERRI ions, the same samples as those of the GE method were prepared. For thermodynamic data to obtain, Hubbard-type PM (Specific Gravity Bottle, Sibata Scientific Technology Ltd.) was used. The sample was also kept at 27 ± 1°C. The data obtained were treated in the same way as that in the preceding paper [4].
4. Results and Discussion
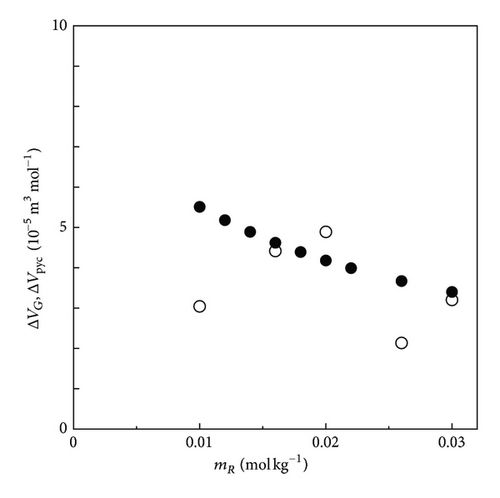
Figure 11 shows the plot of the partial molar volume change in the oxidation of FERRO ion measured by the upward electrode together with the thermodynamic data by the PM method. Both data take positive values, consistent with each other within a relative error of 1.48 × 10−5 m3 mol−1. As discussed above, such agreement is attributed to the shortened lifetime of the ionic vacancy due to the increasing collision efficiency in the convection flow driven by the upward buoyancy forces arising from the vacancy production together with the positive partial molar volume change between FERRO and FERRI ions.
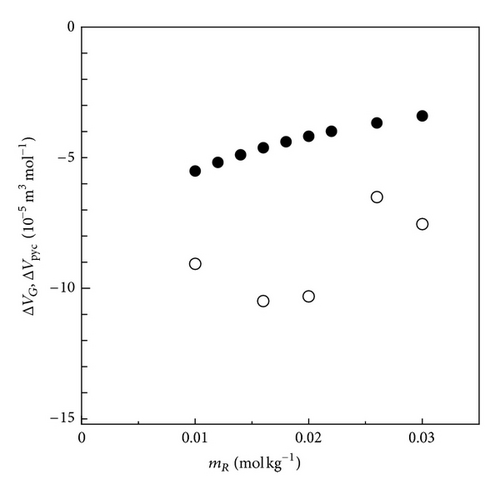
In Figure 12, the partial molar volume change in the reduction of FERRI ion at the downward electrode is exhibited. Different from the above case, all the data are shifted toward the negative side, which is attributed to the negative buoyancy forces occurring from the vacancy extinction together with the negative partial molar volume change between FERRI and FERRO ions, which suggests that the stagnation under the downward electrode keeps the collision of vacancy away, making the lifetime longer.
In Figures 13 and 14, the effective partial molar volumes extracted by (12) are exhibited. For the FERRO ion oxidation in Figure 13, the average value of is nearly equal to zero, that is, −8.77 × 10−6 m3 mol−1. In comparison with the expected value of the ionic vacancy with –1 unit charge given by VV = 2.13 × 10−4 m3 mol−1, it is concluded that the FERRO ion oxidation at the upward electrode not only always assures the validity of the diffusion current equations (7a) and (7b), but also can be used as the blank test for the GE method. On the other hand, for the FERRI ion reduction in Figure 14, due to the negative buoyancy force of ionic vacancy, the takes a negative average value −3.80 × 10−5 m3 mol−1, which, in comparison with the intrinsic value −2.13 × 10−4 m3 mol−1, can be regarded as a meaningful value. The difference between the experimental and the intrinsic values in Figure 14 results from the fact that the intrinsic lifetime of the vacancy is not sufficiently long for complete observation. Accordingly, it is concluded that the exact measurement for the size of ionic vacancy by the GE method requires, at least, an intrinsic lifetime longer than 1 s. Actually, for the ionic vacancy with an intrinsic lifetime of 8.6 s in copper deposition from acidic cupric sulfate solution, as shown in Figure 3, in spite of upward electrode, observed data agreed with the intrinsic value.
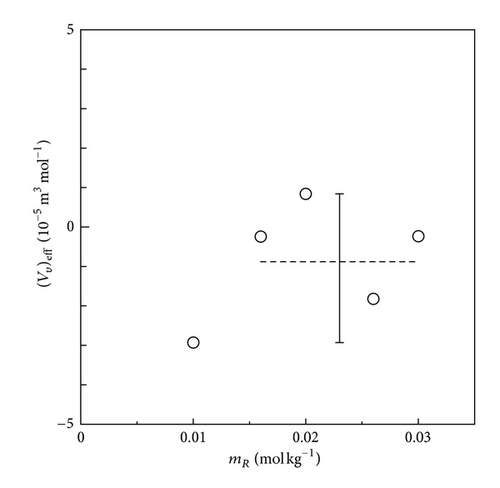
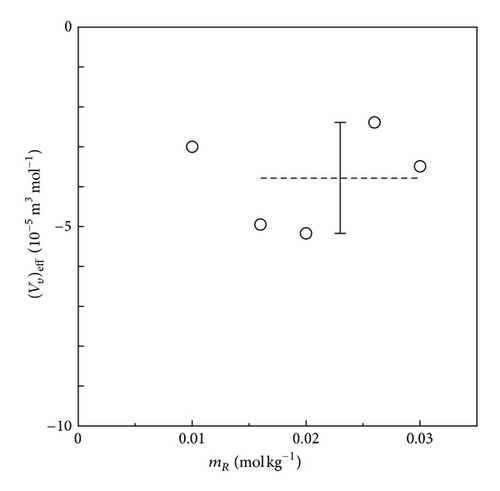
5. Conclusions
In a vertical gravity field, ionic vacancies create partly rigid and partly free surfaces on an electrode surface with and without friction, respectively. However, since the convection flow on the rigid surface is rate-determining step, the whole convection process is controlled by the convection on the rigid surface. Accordingly, it is concluded that in this situation, the same equation as that of rigid surface is derived.
The gravitational convection for FERRI-FERRO ion redox reaction in the GE method arises from the buoyancy force occurring in the reaction, which takes a positive or negative value according to the fact whether the rate-determining step is the production or extinction of ionic vacancy together with the positive or negative partial molar volume change between product and reactant ions. Whether the total buoyancy force of the reaction is positive or negative can be discriminated by the upward or downward electrode used for measuring diffusion current. As a result, it was found that in FERRO ion oxidation and FERRI ion reduction, upward and downward convection cells, arise from the positive and negative buoyancy forces, respectively. However, in the FERRO ion oxidation, the positive partial molar volume of the vacancy from the vacancy production was not observed, whereas in the FERRI ion reduction, the negative partial molar volume from the vacancy extinction was not completely but partly observed. The former result was ascribed to the short vacancy lifetime shortened by the accelerated convection on the upward electrode, and the latter was to the lifetime elongated by the stagnation under the downward electrode.
Acknowledgment
The authors are thankful to Dr. Sugiyama, Waseda University, for providing us with the data of the lifetime of ionic vacancy in FERRI-FERRO redox reaction.
Appendix
The Partial Molar Volume Change Measured by GE in a Redox Reaction
where ρs0 denotes the density of the solvent with the supporting electrolyte.




