Extending Topological Abelian Groups by the Unit Circle
Abstract
A twisted sum in the category of topological Abelian groups is a short exact sequence 0 → Y → X → Z → 0 where all maps are assumed to be continuous and open onto their images. The twisted sum splits if it is equivalent to 0 → Y → Y × Z → Z → 0. We study the class STG(𝕋) of topological groups G for which every twisted sum 0 → 𝕋 → X → G → 0 splits. We prove that this class contains Hausdorff locally precompact groups, sequential direct limits of locally compact groups, and topological groups with ℒ∞ topologies. We also prove that it is closed by taking open and dense subgroups, quotients by dually embedded subgroups, and coproducts. As means to find further subclasses of STG(𝕋), we use the connection between extensions of the form 0 → 𝕋 → X → G → 0 and quasi-characters on G, as well as three-space problems for topological groups. The subject is inspired on some concepts known in the framework of topological vector spaces such as the notion of 𝒦-space, which were interpreted for topological groups by Cabello.
1. Introduction and Preliminaries
In the theory of topological vector spaces (topological groups) a property P is said to be a 3-space property if whenever a closed subspace (subgroup) Y of a space (group) X and the corresponding quotient X/Y both have property P, X also has property P.
A short exact sequence of topological vector spaces (topological groups) will be called a twisted sum, and the space (group) X will be called an extension of Z by Y when both ı and π are continuous and open onto their images. Using this language, 3-space properties can be described as those which are preserved by forming extensions.
An example of a 3-space property in the category of Banach spaces is reflexivity. However, the point-separating property (i.e., having a dual space which separates points) is not a 3-space property. (Consider the space lp for 0 < p < 1, and a weakly closed subspace M of lp without the Hahn-Banach extension property. If we take as N the kernel of some continuous linear functional on M which does not extend to lp, then X = lp/N does not have the point-separating property but both L : = M/N and X/L have this property (see [1])).
In the category of topological Abelian groups, local compactness, precompactness, metrizability, and completeness are 3-space properties. However, σ-compactness, sequential completeness, realcompactness, and a number of other properties are not (see [2] for more examples).
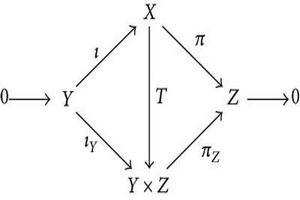
It is known that if such a T exists, it must actually be a topological isomorphism.
If the twisted sum splits and both Y and Z have a productive property P, then X has property P, too.
Kalton et al. provided in [1] the first formal and extensive study of splitting twisted sums in the framework of F-spaces (complete metric linear spaces). They devote Chapter 5 of this monograph to the following problem: is local convexity a 3-space property?
On the path to answering (in the negative) this question, the authors mention a useful result by Dierolf (1973) which asserts that there exists a non-locally-convex extension of the F-space Z by the F-space Y if and only if there exists a non-locally-convex extension of Z by ℝ. The analogue of this result for topological groups, which involves the notion of local quasi-convexity, was obtained by Castillo in [3].
At this point the following definition, originally introduced in [4], comes across as natural: a F-space X is said to be a 𝒦-space if, whenever Y is an F-space and L is a subspace of Y with dimension one such that Y/L≅X, the corresponding twisted sum splits. The negative answer to the 3-space problem for local convexity is obtained in [1] as a corollary of the fact that ℓ1 is not a 𝒦-space.
The notion of 𝒦-space is relevant on its own, regardless of 3-space properties. Many classical spaces such as Lp (0 < p < ∞), lp (p ≠ 1), or c0 are 𝒦-spaces.
In this paper we will study the natural counterpart of the notion of 𝒦-space for topological groups and its connections with 3-space problems, following the work started by Cabello in [5–7].
For simplicity, and because our methods are applicable for the most part only to Abelian groups, we use additive notation, and denote by 0 the neutral element. We denote by ℕ the set of all positive natural numbers, by ℤ the integers, by ℝ the reals, by ℂ the set of complex numbers, and by 𝕋 the unit circle of ℂ, with the topology induced by ℂ. In 𝕋 we will use multiplicative notation and we will denote by p the canonical projection from ℝ to 𝕋 given by p(t) = exp (2πit). We will use 𝒩0(G) to denote the system of neighborhoods of 0 in a topological Abelian group G.
Recall that a topological Abelian group G is precompact if for every neighborhood of zero V there exists a finite subset F of G such that G = F + V. Precompact groups are the subgroups of compact groups. In the same way a group G is locally precompact if and only if it is a subgroup of a locally compact group.
The dual group G∧ of a given topological Abelian group G is formed from the continuous group homomorphisms from G into 𝕋, usually called characters. The polar set of a subset A of G is defined by A0 : = {χ ∈ G∧ : χ(A)⊆𝕋+}, where 𝕋+ : = p([−1/4,1/4]) = {z ∈ 𝕋 : Re(z) ≥ 0}. A subset A of a topological group G is called quasi-convex if for every x ∈ G∖A there is a χ ∈ A0 such that χ(x) ∉ 𝕋+. A topological group is called locally quasi-convex if it has a neighborhood basis of 0 consisting of quasi-convex sets. It is well known (see [8]) that a topological vector space is locally convex if and only if it is a locally quasi-convex topological group in its additive structure.
If G∧ separates the points of G we say that G is maximally almost periodic (MAP). Every locally quasi–convex group is a MAP group.
The analogous notion to the HBEP (Hahn-Banach Extension Property) for topological groups is the following. A subgroup H ≤ X is dually embedded in X if each character of H can be extended to a character of X.
When endowed with the compact-open topology τco , G∧ becomes a Hausdorff topological group. A basis of neighborhoods of the neutral element for the compact open topology τco is given by the sets K0 = {χ ∈ G∧ : χ(K)⊆𝕋+}, where K is a compact subset of G.
Remark 1. Observe that a necessary condition for the splitting of the twisted sum of topological Abelian groups is that i(H) be a dually embedded subgroup of X.
The following known characterization is essential when dealing with twisted sums in different categories (see [3, Lemma 3.1] for a proof).
Theorem 2. Let be a twisted sum of topological Abelian groups. The following are equivalent:
- (1)
;
- (2)
there exists a continuous homomorphism S : G → X with π∘S = idG, i.e., a right inverse for π;
- (3)
there exists a continuous homomorphism P : X → H with P∘ı = idH, i.e., a left inverse for ı.
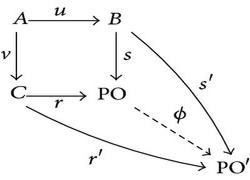
and such that for every topological Abelian group PO′ and continuous homomorphisms r′ : C → PO′ and s′ : B → PO′ with s′∘u = r′∘v, there is a unique continuous homomorphism ϕ from PO to PO′ making the two triangles commutative. The topological group PO exits and is unique up to topological isomorphism.
where both squares are commutative and the bottom sequence is a twisted sum [3].
An analogous result for the dual construction (the pull-back) can be obtained (see [3]).
Lemma 3. Let K be a compact subgroup of a topological Abelian group X. X∧ separates points of K if and only if K is dually embedded in X.
Proof. Suppose that X∧ separates points of K. It is known that for any locally compact Abelian group G, a subgroup L ≤ G∧ is dense in G∧ if and only if it separates points of G (see [9, Proposition 31]). The subgroup L of K∧ formed by all restrictions of characters of X separates points of K by hypothesis. Hence L is dense in K∧ and, as K∧ is discrete, L coincides with K∧.
Suppose that K is dually embedded in X. As K is compact, it is a MAP group. Fix a nonzero x ∈ K. There exists χ ∈ K∧ such that χ(x) ≠ 1. Since K is dually embedded in X, there exists an extension of χ with .
Corollary 4 ([10, Proposition 1.4]). Let K be a compact subgroup of a topological Abelian group X. If X is maximally almost periodic, then K is dually embedded in X.
2. The Class
Next we consider the particular case in which the compact subgroup K is 𝕋. (The proofs of Theorems 5 and 7 below can be extracted from that of [3, Theorem 4.1], but we prefer the present formulation.)
Theorem 5. Let be a twisted sum of topological Abelian groups. The following are equivalent:
- (1)
the twisted sum splits;
- (2)
X∧ separates points of ı(𝕋);
- (3)
ı(𝕋) is dually embedded in X.
Proof. 2⇔3 is a corollary of Lemma 3.
3⇒1: suppose that ı(𝕋) is dually embedded in X. Hence there exists a continuous character χ : X → 𝕋 which extends the isomorphism φ : ı(𝕋) → 𝕋 defined by φ(ı(t)) = t. Since χ∘ı = id𝕋, the assertion follows from Theorem 2.
1⇒2: fix x ∈ ı(𝕋), x = ı(z) with z ≠ 1. By Theorem 2, there exists a continuous homomorphism P : X → 𝕋 with P∘ı = id𝕋; hence P(ı(z)) = id𝕋(z) = z ≠ 1.
Now we will complete the previous Theorem under the assumption that G is locally quasi-convex. We will use the following result due to Castillo, concerning the 3-space problem in locally quasi-convex groups.
Lemma 6 ([3, Theorem 2.1]). Let H be a locally quasi-convex subgroup of a topological Abelian group X such that X/H is locally quasi-convex. Then X is locally quasi-convex if and only if H is dually embedded in X.
Theorem 7. Let be a twisted sum of topological Abelian groups. Suppose that G is locally quasi-convex. Then conditions (1), (2), (3) of Theorem 5 are equivalent to
- (4)
X is locally quasi-convex.
Proof. 1⇒4: if the twisted sum splits, X is topologically isomorphic to the product of two locally quasi-convex groups; hence it is locally quasi-convex.
4⇒3: given a twisted sum with X and G locally quasi-convex, since G≅X/ı(𝕋), by Lemma 6, we deduce that ı(𝕋) is dually embedded in X.
Following the notation used by Domański [11] in the framework of topological vector spaces, we introduce the class S TG (𝕋) which is the analogue of that of 𝒦-spaces for topological Abelian groups.
Definition 8. We say that a topological Abelian group G is in the class S TG (𝕋) if every twisted sum of topological Abelian groups 0 → 𝕋 → X → G → 0 splits.
Theorem 9. Let G be a topological vector space such that G ∈ S TG (𝕋) as a topological group. Then G is a 𝒦-space.
Proof. Suppose that G ∈ S TG (𝕋). Fix a twisted sum of topological vector spaces . Recall that we denote by p : ℝ → 𝕋 the canonical projection, given by p(r) = exp (2πir). If we consider the push-out PO of p and ı, we obtain a commutative diagram
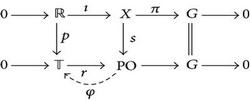
where the bottom sequence is a twisted sum. Since G ∈ S TG (𝕋), this sequence splits. Hence there exists a left inverse φ for r. Then φ∘s∘ı = p. Since X is a topological vector space, φ∘s is of the form x ↦ exp (2πif(x)) for some continuous linear functional f ∈ X*. This clearly implies f∘ı = idℝ; that is, f is a left inverse for ı; hence the top sequence splits, too.
Theorem 10 ([4, 12, 13]). There is a short exact sequence of topological vector spaces and continuous, relatively open linear maps which does not split. In other words, ℓ1 is not a 𝒦-space.
Using Theorem 9 we deduce the following.
Corollary 11. ℓ1 ∉ S TG (𝕋).
Remark 12. The above corollary gives an example of a quotient X/𝕋 which is locally quasi-convex as a topological group but such that X does not even separate points of 𝕋: a strong failure of the 3-space property for local quasi-convexity and for the property of being a MAP group.
From Theorem 5 it follows that a topological Abelian group G is in S TG (𝕋) iff for every twisted sum of topological Abelian groups of the form , the subgroup ı(𝕋) is dually embedded in X. Note that in any such twisted sum, for an arbitrary A ≤ G the subgroup π−1(A) contains ı(𝕋). This yields the following criterion;
Proposition 13. Let G be a topological Abelian group. Suppose that there exists a subgroup A ≤ G which is in STG(𝕋) and satisfies the following property. For every twisted sum of topological Abelian groups of the form , the subgroup π−1(A) is dually embedded in X. Then .
Corollary 14. Let G be a topological Abelian group. Suppose that there exists an open subgroup A ≤ G such that A ∈ STG(𝕋). Then G ∈ STG(𝕋).
Proof. If A is an open subgroup of G, with the notation of Proposition 13, π−1(A) is an open subgroup of X and hence dually embedded.
Corollary 15. Let G be a topological Abelian group. Suppose that there exists a dense subgroup A ≤ G such that A ∈ STG(𝕋). Then G ∈ STG(𝕋).
Proof. If A is a dense subgroup of G, with the notation of Proposition 13, π−1(A) is a dense subgroup of X because π is continuous and onto. In particular it is dually embedded in X.
We next see that the converse of Corollary 15 is true in the case of G metrizable. For any topological Abelian group G, we denote by the Raĭkov completion of G. See [14] for more information about this subject.
Lemma 16 ([14, Theorem 6.11]). If G is a metrizable topological group that has a completion and if H is a closed normal subgroup of G, then G/H has a completion that is topologically isomorphic to , where is the closure of H in .
Proposition 17. Let G be a metrizable topological Abelian group which is in . Suppose that A is a dense subgroup of G. Then A is in STG(𝕋), too.
Proof. Let X be a topological Abelian group, and let 𝕋≅L ≤ X be a subgroup such that A≅X/L. Since metrizability is a 3-space property ([15, 5.38(e)]), X is a metrizable group. By Lemma 16, . By Corollary 15, . It follows that L is dually embedded in ; hence it is dually embedded in X, too.
Our next aim is to prove that Hausdoff locally precompact groups are in S TG (𝕋). Note first that if G is a topological Abelian group and H ≤ G is a precompact subgroup such that the quotient G/H is locally precompact, then G is locally precompact, too. (Indeed, let π : G → G/H be the canonical projection. Choose U ∈ 𝒩0(G) such that π(U) is precompact. Let us see that U is precompact. Given V ∈ 𝒩0(G) we need to find a finite subset F ⊂ G with U ⊂ F + V. Fix V′ ∈ 𝒩0(G) with V′ + V′ ⊂ V and find a finite F1 ⊂ G with H ⊂ F1 + V′. Since π(U) is precompact there exists a finite subset of G/H with . We may suppose that with F2 being a finite subset of G. Hence π(U) ⊂ π(F2) + π(V′) = π(F2 + V′), which implies U ⊂ π−1π(U) ⊂ π−1π(F2 + V′) = F2 + V′ + H ⊂ F1 + F2 + V′ + V′ ⊂ F + V if we put F = F1 + F2.)
Theorem 18. Locally precompact Hausdorff Abelian groups are in STG(𝕋).
Proof. Let G be a locally precompact Hausdorff Abelian group. Given a twisted sum , as 𝕋 is in particular precompact, by the above argument X is locally precompact, too. But every subgroup of a locally compact group is dually embedded [15, 24.12], so ı(𝕋) is dually embedded in , the completion of X. Then ı(𝕋) is also dually embedded in X and by Theorem 5, the twisted sum splits.
Corollary 19. Locally compact Hausdorff Abelian groups and precompact Hausdorff Abelian groups are in STG(𝕋).
Remark 20. It is proved in [11] that every topological vector space endowed with its weak topology is a 𝒦-space. The above corollary shows that a similar result is true for topological Abelian groups, since a topological group endowed with the topology induced by its characters is precompact (see [16]).
Theorem 21. Let G be a topological Abelian group.
- (1)
If a closed subgroup H ≤ G is such that G/H ∈ STG(𝕋), then H is dually embedded.
- (2)
If G is in STG(𝕋) and H ≤ G is a closed dually embedded subgroup, then G/H ∈ STG(𝕋).
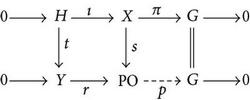
Proof. (1) Suppose that G/H ∈ S TG (𝕋). Let χ : H → 𝕋 be a character, and consider the natural twisted sum . By taking the corresponding push out, we obtain the following commutative diagram:
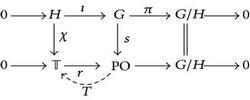
where both rows are twisted sums of topological Abelian groups. Since G/H ∈ S TG (𝕋), the bottom sequence splits; hence by Theorem 2, there exists a continuous homomorphism T : PO → 𝕋 such that T∘r = id𝕋. The homomorphism T∘s is an extension of χ.
(2) Suppose that H is dually embedded in G. Fix a twisted sum . Let q : G → G/H be the canonical projection, and let PB = {(g, x) ∈ G × X : q(g) = π(x)} be the pull-back of q and π. Define r : PB → G and s : PB → X, as the restrictions of the corresponding projections. Note that
We thus obtain the following diagram:
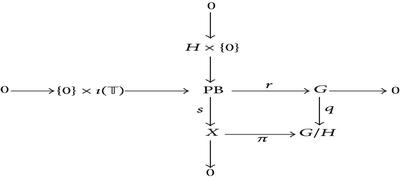
Note that since q and π are onto, the definition of PB yields r((U × X)∩PB)⊃U and s((G × V)∩PB)⊃V for every U ∈ 𝒩0(G) and V ∈ 𝒩0(X); hence r and s are onto and open. Thus both short sequences are twisted sums of topological Abelian groups.
Fix φ ∈ ı(𝕋) ∧; we will find an extension of φ to the whole X. We can regard φ as a character of {0} × ı(𝕋) by defining . Since {0} × ı(𝕋)≅𝕋 and G ∈ S TG (𝕋), by Theorem 5, {0} × ı(𝕋) is dually embedded in PB. Thus there exists ψ ∈ PB∧ with ; that is, ψ(0, x) = φ(x) for every x ∈ ı(𝕋). Define, for every h ∈ H, (note that if h ∈ H then (h, 0) ∈ PB).
Since H is dually embedded in G there exists σ ∈ G∧ with i.e. σ(h) = ψ(h, 0) for every h ∈ H. Now define ρ ∈ PB∧ as follows: . This is clearly continuous. Note that ker ρ ≥ ker s = H × {0} since if h ∈ H, we have that . As X≅PB/(H × {0}), the character in X∧ given by for every (g, x) ∈ PB is well defined and continuous.
Now is the desired extension of φ: if x ∈ ı(𝕋), we have .
Remark 22. An analogous result in the framework of F-spaces is [1, Theorem 5.2] (cf. also [11, Lemma 4.1]).
The following corollary is a generalization of Theorems 5.2 and 5.3 in [4] and appears as Theorem 4.1 in [3].
Corollary 23. A topological Abelian group G is in S TG (𝕋) if and only if whenever X is a topological Abelian group and H is a closed subgroup of X with X/H≅G, then H is dually embedded.
Let (Gα) α∈I be a family of topological Abelian groups. The coproduct of (Gα) α∈I is the direct sum ⨁α∈IGα endowed with the finest group topology making the inclusion maps iβ : Gβ↪⨁α∈IGα continuous, for every β ∈ I. If is a countable family of groups, this topology coincides with the box topology on ⨁n∈ℕGn.
Recall that the coproduct ⨁α∈IGα has the following universal property. Given an arbitrary topological Abelian group G and a homomorphism f : ⨁α∈IGα → G, f is continuous if and only if f∘iβ is continuous ∀β ∈ I.
Proposition 24. Let (Gα) α∈I be a family of topological Abelian groups in S TG (𝕋). The coproduct ⨁α∈IGα is in S TG (𝕋).
Proof. Let be a twisted sum. Consider, for each β ∈ I, the pull-back PBβ of π and iβ : Gβ → ⨁α∈IGα; for every β ∈ I there is a commutative diagram
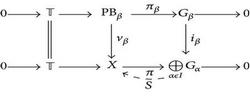
so S is a right inverse for π, and again by Theorem 2, the initial twisted sum splits.
The class of nuclear groups was formally introduced by Banaszczyk in [8]. His aim was to find a class of topological groups enclosing both nuclear spaces and locally compact Abelian groups (as natural generalizations of finite-dimensional vector spaces). The original definition is rather technical, as could be expected from its success in gathering objects from such different classes into the same framework. Next we collect some facts concerning the class of nuclear groups which are relevant to this paper.
- (i)
Nuclear groups are locally quasi-convex [8, 8.5].
- (ii)
Subgroups of nuclear groups are dually embedded [8, 8.3].
- (iii)
Products, countable coproducts, subgroups, and Hausdorff quotients of nuclear groups are nuclear [8, 7.6, 7.8, 7.5].
- (iv)
Every locally compact Abelian group is nuclear [8, 7.10].
- (v)
A nuclear locally convex space is a nuclear group [8, 7.4]. Furthermore, if a topological vector space is a nuclear group, then it is a locally convex nuclear space [8, 8.9].
Theorem 25. Let be a countable direct system of nuclear Abelian groups in S TG (𝕋). Then the direct limit lim → Gn is in S TG (𝕋). In particular, sequential direct limits of locally compact groups are in S TG (𝕋).
Proof. The direct sum with the coproduct topology is in S TG (𝕋) by Proposition 24. Let im : Gm → ⨁ Gn be the inclusion map, for every m ∈ ℕ. It is known (see [17]) that , where is the closure of the subgroup H generated by . Since countable coproducts of nuclear groups are nuclear groups, is dually embedded. By Theorem 21, lim → Gn ∈ S TG (𝕋).
Varopoulos introduced in [18] the class ℒ∞ of all topological groups whose topologies are the intersection of a decreasing sequence of locally compact Hausdorff group topologies. He succeeded in his aim of extending known results about locally compact groups and established the basis for the development of the harmonic analysis on ℒ∞ groups. Subsequently many other authors investigated different properties of this class ([19–23]).
The following is a relevant fact concerning the structure of ℒ∞ groups proved by Sulley.
Proposition 26 ([22]). Let G be any Abelian group endowed with an ℒ∞ topology. Then G has an open subgroup which is a strict inductive limit of a sequence of Hausdorff locally compact Abelian groups.
Corollary 27. Let G be any Abelian group endowed with an ℒ∞ topology. Then G is in S TG (𝕋).
3. Quasi-Homomorphisms
In his study of the stability of homomorphisms between topological Abelian groups [7], Cabello defined the notion of quasi-homomorphism, which is inspired by the technique of quasi-linear maps introduced by Kalton and others (see [1]).
Definition 28 ([7]). Let G and H be topological Abelian groups and ω : G → H a map with ω(0) = 0. We say that ω is a quasi-homomorphism if the map Δω : (x, y) ∈ G × G ↦ ω(x + y) − ω(x) − ω(y) ∈ H is continuous at (0,0).
A quasi-homomorphism ω : G → H is approximable if there exists a homomorphism a : G → H such that ω − a is continuous at 0.
Our aim is to use the notion of approximable quasi-homomorphisms to obtain new examples of groups in S TG (𝕋).
We start with some facts about quasi-homomorphism taken from [7].
Proposition 29. Let G and H be topological Abelian groups and ω : G → H a quasi-homomorphism.
- (1)
The sets
() -
form a basis of neighborhoods of zero for a group topology on H × G.
- (2)
If H⨁ωG denotes the group H × G endowed with the topology induced by the quasi-homomorphism ω and ıH and πG denote the canonical inclusion and projection, respectively, is a twisted sum of topological Abelian groups.
- (3)
A quasi-homomorphism is approximable if and only if the induced twisted sum splits.
- (4)
The twisted sum is equivalent to one induced by a quasi-homomorphism if and only if it splits algebraically and there exists a map ρ : G → X such that π∘ρ = idG, ρ(0) = 0 and ρ is continuous at the origin.
Lemma 30. Let G and H be topological Abelian groups and ω : G → H a quasi-homomorphism. Then the map g ∈ G ↦ (ω(g), g) ∈ H⨁ωG is continuous at 0.
Proof. Note that for every U ∈ 𝒩0(G) and V ∈ 𝒩0(H) we have [g ∈ U⇒(ω(g), g) ∈ W(V, U)].
The following result is [7, Lemma 11]. We give here a proof for the sake of completeness.
Proposition 31. Let π : X → G be a continuous and open surjective homomorphism between topological Abelian groups. Suppose that X is metrizable. Then there exists ρ : G → X such that π∘ρ = idG and ρ is continuous at 0 ∈ G.
Proof. Note that in order to define ρ with π∘ρ = idG, we simply must choose for every g ∈ G an element x ∈ π−1(g), which is a nonempty set since π is onto. Let us see that it can be done in such a way that the map thus obtained is continuous at zero.
Let {Un : n ∈ ℕ} be a decreasing basic sequence of neighborhoods of zero in X, where U1 = X. Due to the continuity of π, we have ⋂n∈ℕ π(Un) = {0}. Let ρ take the value 0 on g = 0. For any g ≠ 0, by the previous paragraph, we can choose n and x with π(x) = g, x ∈ Un, g ∉ π(Un+1), and define ρ(g) = x. Now fix m ∈ ℕ; we must find V ∈ 𝒩0(G) with ρ(V)⊆Um. Since π is open there exists V ∈ 𝒩0(G) with π(Um)⊇V. Fix g ∈ V, and let us show that ρ(g) ∈ Um. If ρ(g) = 0 this is trivial. Otherwise ρ(g) = x with π(x) = g, x ∈ Un, g ∉ π(Un+1) for some n. Then g ∈ V⊆π(Um); hence m ≤ n and x ∈ Un⊆Um.
Corollary 32. Let G be a metrizable topological Abelian group.
- (1)
If H is metrizable and divisible, every twisted sum is equivalent to one induced by a quasi-homomorphism.
- (2)
G is in S TG (𝕋) if and only if every quasi-character ω : G → 𝕋 is approximable.
Proof. Metrizability is a 3-space property (see [15, 5.38(e)]). If is a twisted sum where both G and H are metrizable, so is X, and thus the hypotheses of Proposition 31 hold. Therefore, there exists a section of π continuous at the origin. As H is a divisible group, the twisted sum splits algebraically. By Proposition 29(4), this twisted sum is equivalent to one induced by a quasi-homomorphism.
The second part is a consequence of the first one and Proposition 29(3).
We call a norm on an Abelian group G any subadditive, symmetric functional ∥·∥ : G → [0, ∞) such that ∥x∥ = 0 if and only if x = 0.
Definition 33. For any t ∈ 𝕋 let us call 〈t〉 the only real number α ∈ ] − 1/2,1/2] such that exp (2πiα) = t. Then [t→|〈t〉|] is a norm on 𝕋. (Note that 〈ts〉∈〈t〉+〈s〉+ℤ; hence |〈ts〉|≤|〈t〉+〈s〉|≤|〈t〉|+|〈s〉.) Put θ(t) = |〈t〉|. For every β > 0 let us define Tβ = {t ∈ 𝕋 : θ(t) ≤ β}. Note that 𝕋+ = T1/4 with this notation.
Definition 34. For every Abelian group G, every V⊆G with 0 ∈ V, and every n ∈ ℕ we define (1/2n)V = {x ∈ V : 2kx ∈ V ∀ k ∈ {0,1, …, n}}.
Proposition 35 ([24, Corollary 2]). For every n ∈ ℕ ∪ {0} and β ∈ [0,1/3), we have .
Lemma 36. Let G be a topological Abelian group, and let ω : G → 𝕋 be a quasi-character. Suppose that there exist U ∈ 𝒩0(G) and β ∈ (0,1/3) such that ω(U)⊆Tβ. Then ω is continuous at zero.
Proof. Since ω is a quasi-character, for every ρ > 0, there exists Wρ ∈ 𝒩0(G) with for every u ∈ Wρ. Fix any ɛ > 0. Let us find V ∈ 𝒩0(G) with ω(V)⊆Tɛ.
Fix any β′ ∈ (β, 1/3). Find N ∈ ℕ with β′/2N ≤ ɛ. Put .
It is enough to prove that
since by Proposition 35, this will imply . Now, for every n ∈ {0,1, 2, …, N}
Corollary 37. A quasi-character ω : G → 𝕋 is approximable if and only if there exist U ∈ 𝒩0(G), β ∈ (0,1/3) and an algebraic character χ ∈ Hom (G, 𝕋) such that . Moreover any such χ approximates ω.
Lemma 38 ([7, Lemma 6]). Let G be an Abelian group (no topology is assumed), and let ω : G → 𝕋 be any mapping such that for some β < 1/3, . Then there is a unique character χ : G → 𝕋 such that .
Theorem 39. Let μ be a nonatomic σ-finite measure on a set Δ. Let L0 : = L0(μ) be the space of all measurable functions on Δ with the norm
Proof. We can assume, without loss of generality, that μ is a probability (note that L0(μ) is topologically isomorphic to L0(ν), where ν is a probability with the same null sets as μ).
Let ω : L0 → 𝕋 be a quasi-character, fix β < 1/3, and choose δ0 such that for every f, g with ∥f∥0, ∥g∥0 ≤ δ0.
Let be a partition of Δ into measurable sets, with μ(Δi) ≤ δ0 for all 1 ≤ i ≤ r. Then as a topological direct product. For all f ∈ L0(Δi) we have that
Corollary 40. L0 is in S TG (𝕋).
Example 41. Let L0 be as in Theorem 39. Fix a discrete, nontrivial D ≤ L0 (e.g., a copy of ℤ). Note that L0 does not have any nontrivial continuous character, and in particular D is not dually embedded in L0. Using Theorem 21 we deduce that L0/D is not in S TG (𝕋). Since L0 ∈ S TG (𝕋), this example shows that being in S TG (𝕋) is not preserved by local isomorphisms (compare with Corollary 14).
Let (G, τ) be a topological group. We say that (G, τ) is a protodiscrete group (or that the topology τ is linear) if it has a basis of neighborhoods of 0 formed by open subgroups. Note that protodiscrete Hausdorff groups are exactly the subgroups of products of discrete groups.
Proposition 42. Let G be a protodiscrete topological Abelian group. Every quasi-character of G is approximable.
Proof. Let ω : G → 𝕋 be a quasi-character. There exists an open subgroup U ≤ G such that for every a, b ∈ U. Using Lemma 38 we deduce that there exists an algebraic character χ : U → 𝕋 with for every u ∈ U. Now Corollary 37 implies that any algebraic extension of χ approximates ω.
Corollary 43. Every protodiscrete, metrizable group is in S TG (𝕋).
Example 44. Countable products of discrete Abelian groups belong to S TG (𝕋).
Acknowledgments
The authors acknowledge the financial support of Spanish MICINN (Grant MTM2009-14409-C02-01), and of University of Navarra (PIUNA Grant). The third listed author acknowledges support of Consellería de Educación e Ordenación Universitaria (Xunta de Galicia, Grant CN2011/002) and FEDER funds.




