Abstract and Applied Analysis
Volume 2013, Issue 1 573782
Research Article
Open Access

Variational Iteration Method for the Magnetohydrodynamic Flow over a Nonlinear Stretching Sheet

Lan Xu, 

Lan Xu

National Engineering Laboratory for Modern Silk, College of Textile and Engineering, Soochow University, 199 Ren-ai Road, Suzhou, Jiangsu 215123, China suda.edu.cn

Nantong Textile Institute of Soochow University, 58 Chong-chuan Road, Nantong, Jiangsu 226018, China suda.edu.cn

Search for more papers by this author
Eric W. M. Lee, 

Corresponding Author

Eric W. M. Lee

Department of Civil and Architectural Engineering, City University of Hong Kong, 83 Tat Chee Avenue, Kowloon Tong, Kowloon, Hong Kong cityu.edu.hk

Search for more papers by this author
First published: 20 March 2013
https://doi.org/10.1155/2013/573782
Citations: 16
Academic Editor: de Dai

Abstract

The variational iteration method (VIM) is applied to solve the boundary layer problem of magnetohydrodynamic flow over a nonlinear stretching sheet. The combination of the VIM and the Padé approximants is shown to be a powerful method for solving two-point boundary value problems consisting of systems of nonlinear differential equations. And the comparison of the obtained results with other available results shows that the method is very effective and convenient for solving boundary layer problems.

1. Introduction

It is well known that most of the phenomena that arise in mathematical physics and engineering fields can be described by partial differential equations. Recent advances of partial differential equations are stimulated by new examples of applications in fluid mechanics, viscoelasticity, mathematical biology, electrochemistry, and physics. There are many traditional and recently developed methods to give numerical and analytical approximate solutions of nonlinear differential equations such as Euler method, Runge-Kutta method, Taylor series method, Adomian decomposition method [1], Variational iteration method [2, 3], Hankel-Padé method [4], DTM-Padé method [5], homotopy perturbation method [6], and Hamiltonian method [7].

In this paper, we consider the model proposed by authors in [1] describing the problem of the boundary layer flow of an incompressible viscous fluid over a nonlinear stretching sheet. The boundary layer flow is often encountered in many engineering and industrial processes. Such processes include the aerodynamic extrusion of plastic sheets, hot rolling, glass fiber production, and so on [1, 4, 5]. And various aspects of the stretching flow problem were discussed by various investigators. Chiam [8] analyzed the MHD flow of a viscous fluid bounded by a stretching surface with power law velocity. He presented the numerical solution of the boundary value problem by utilizing the Runge-Kutta shooting algorithm with Newton iteration. Here, we aim to solve the MHD flow caused by a sheet with nonlinear stretching. The approximate solution of the nonlinear problem is obtained by the variational iteration method.

The variational iteration method [2] is a type of Lagrange multiplier method to find analytical solutions. The method gives the possibility to solve many kinds of non linear equations. In this method, general Lagrange multipliers are introduced to construct correction functional for the problems. The multipliers can be identified optimally via variational theory. It has been used to solve effectively, easily, and accurately a large class of nonlinear problems with approximation [9].

2. Basic Idea of the VIM

The basic idea was systematically illustrated and discussed in [9, 10]. To illustrate the basic idea of the VIM, we consider the following general nonlinear system:
()
where L, N, and g(t) are the linear operator, the nonlinear operator, and a given continuous function, respectively. The basic character of the method is to construct a correction functional for the system, which reads
()
where λ is a Lagrange multiplier which can be identified optimally via the variational theory. The subscript n indicates the nth approximation, and denotes a restricted variation, that is, .

3. Problem Statement and Governing Equations

We consider the magnetohydrodynamic (MHD) flow of an incompressible viscous fluid over a stretching sheet at y = 0. The fluid is electrically conducting under the influence of an applied magnetic field B(x) normal to the stretching sheet. The induced magnetic field is neglected. The resulting boundary layer equations are as follows [1]:
()
()
where u and v are the velocity components in the x and y directions, respectively, ν is the kinematic viscosity, ρ is the fluid density, and σ is the electrical conductivity of the fluid. In (4), the external electric field and the polarization effects are negligible, and in [8]
()
The boundary conditions corresponding to the nonlinear stretching of a sheet are
()
Upon making use of the following substitutions:
()
()
Substituting (8) into (3)–(6), the resulting nonlinear differential system can be written in the following form:
()
()
where
()
The parameter β is a measure of the pressure gradient, and M is the magnetic parameter. Positive β denotes the favorable negative pressure gradient, and negative β denotes the unfavorable positive pressure gradient; naturally, β = 0 denotes the flat plate. For the special case of β = 1, the exact analytical solution of (9) is [11]
()

4. Approximate Solution by the VIM

In order to obtain VIM solution of (9), we construct a correction functional which reads
()
where λ(τ) is the general Lagrangian multiplier which can be identified optimally via the variational theory. And is considered as a restricted variation, that is, . We omit asterisks for simplicity. Its stationary conditions can be obtained as follows:
()
The Lagrange multipliers can be readily identified as the following form:
()
As a result, we obtain the following variational iteration formula
()
Now, we assume that an initial approximation
()
where a,   b, and c are unknown constants to be further determined.
By the iteration formula (16) and the initial approximation (17), we can obtain directly the first-order approximate solution as follows:
()
Making use of the initial conditions f(0) = 0,   f′(0) = 1, we can readily obtain the results as follows:
()
where f′′(0) = α will be examined in this work, according the initial condition f′(∞) = 0.
Then,
()
And the following second-order approximate solution can be obtained
()
Therefore, according to (13), we can easily obtain higher-order approximate solution as follows:
()
by using mathematical software such as MATLAB.

It is evident that the main problem for solving (21) is to obtain the value of f′′(0), then we can resort to any numerical integration routine to obtain the solution of the problem. For this purpose, we will employ the Padé method to determine this unknown value with high accuracy.

5. Padé Approximation

It is well known that Padé approximations [12] have the advantage of manipulating the polynomial approximation into a rational function of polynomials. This manipulation provides us with more information about the mathematical behavior of the solution. Besides that, power series are not useful for large values of η, say η = ∞. This can be attributed to the possibility that the radius of convergence may not be sufficiently large to contain the boundaries of the domain. Therefore, the combination of the series solution through the decomposition method or any other series solution method with the Padé approximation provides an effective tool for handling boundary value problems on infinite or semi-infinite domains. Furthermore, it is noted that Padé approximants can be easily evaluated by using Matlab.

Therefore, we suppose that the solution f(η) can be expanded as a Taylor series about η = 0
()
Padé approximant, symbolized by [S/N], is a rational function defined by
()
If we selected S = N, then the approximants [N/N] are called diagonal approximants. More importantly, the diagonal approximants are the most accurate approximants; therefore, we have to construct only diagonal approximants.
Then,
()
By using cross multiplication in (25), we find
()
Using the boundary condition f′(∞) = 0, the diagonal approximant [N/N] vanishes if the coefficient of η with the highest power in the numerator vanishes. By putting the coefficients of the highest power of η equal to zero, we can easily obtain the values of f′′(0) listed in Tables 1 and 2 and Figure 1, using Matlab. The order of Padé approximation [12/12] has sufficient accuracy; on the other hand, if the order of Padé approximation increases, the accuracy of the solution increases.
Table 1. Comparison of the values of f′′(0) obtained by the variational iteration method and other methods [1] for various values of M when β = 1.
M VIM ADM [1] Exact [1]
1.0 −1.41421 −1.41421 −1.41421
5.0 −2.44948 −2.44948 −2.44948
10.0 −3.31662 −3.31662 −3.31662
50.0 −7.14142 −7.14142 −7.14142
100.0 −10.04987 −10.04987 −10.04987
500.0 −22.38302 −22.38302 −22.38302
Table 2. Comparison of the values of f′′(0) obtained by the variational iteration method and the modified Adomian decomposition method [1] for various values of β and M.
M β = −1.5 β = 1.5 β = 5
VIM ADM [1] VIM ADM [1] VIM ADM [1]
1.0 −0.6530 −0.6532 −1.5253 −1.5252 −2.1529 −2.1528
5.0 −2.0852 −2.0852 −2.5162 −2.5161 −2.9414 −2.9414
10 −3.0562 −3.0562 −3.3663 −3.3663 −3.6957 −3.6956
50 −7.0239 −7.0239 −7.1647 −7.1647 −7.3256 −7.3256
100 −9.9667 −9.9666 −10.0776 −10.0776 −10.1816 −10.1816
500 −22.3458 −22.3457 −22.3905 −22.3904 −22.4426 −22.4425
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Comparison between the approximate solution by the VIM and exact solution for β = 1 and M = 10.

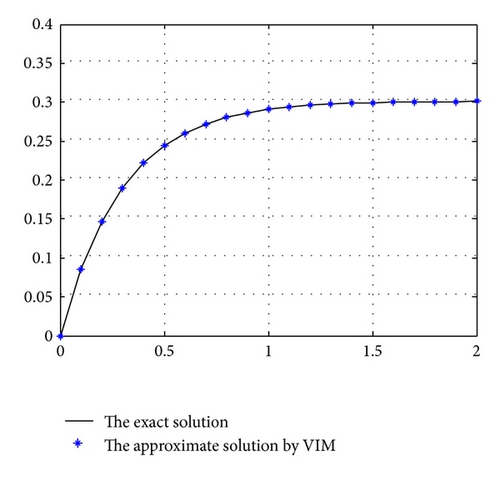
Substituting (21) and the value of f′′(0) into (8), we can easily obtain the second-order approximate solution of (3)-(4).

6. Conclusion

In this paper, the variational iteration method is used to obtain approximate solutions of magnetohydrodynamics boundary layer equations. The analytical solutions of the governing nonlinear boundary layer problem are obtained. Without using the Padé approximation, the analytical solution that were obtained by the VIM cannot satisfy the boundary condition at infinity f′(∞) = 0. The combination of the VIM and the Padé approximants is shown to be a powerful method for solving two-point boundary value problems consisting of systems of nonlinear differential equations. And the obtained solutions are in good agreement with exact values.

Acknowledgments

The work described in this paper was fully supported by a grant from the Research Grants Council of the Hong Kong Special Administrative Region, China (CityU 116308) and Natural Science Foundation of the Jiangsu Higher Education Institutions of China (Grant no. 12KJB130002).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.