Approximate Analytic Solutions of Time-Fractional Hirota-Satsuma Coupled KdV Equation and Coupled MKdV Equation

1. Introduction

In the last past decade, the fractional differential equations have been widely used in various fields of physics and engineering. The analytical approximation of such problems has attracted great attention and became a considbased onerable interest in mathematical physics. Some powerful methods including the homotopy perturbation method [1], Adomian decomposition method [2, 3], variational iteration method [4, 5], homotopy analysis method [6, 7], fractional complex transform method [8], and generalized differential transform method [9] have been developed to obtain exact and approximate analytic solutions. These solution techniques are more clear and realistic methods for fractional differential equations, because they give the approximate solutions of the considered problems without any linearization or discretization.

The variational iteration method and the homotopy perturbation method were first proposed by Professor He in [10, 11], respectively. The idea of the variational iteration method is to construct correction functionals using general Lagrange multipliers identified optimally via the variational theory, and the initial approximations can be freely chosen with unknown constants. Recently, Wu and Lee proposed a fractional variational iteration method for fractional differential equation based on the modified Riemann CLiouville derivative, which is more effective to solve fractional differential equation [12]. This method has been developed by many authors, see [13–16] and the references cited therein. The homotopy perturbation method, which does not require a small parameter in an equation, has a significant advantage that it provides an analytical approximate solution to a wide range of nonlinear problems in applied sciences. Recently, the fractional complex transform is developed to convert the fractional differential equation to its differential partner and gave a geometrical explanation [8]. These methods are more effective for solving the linear and nonlinear fractional differential equations.

The differential transform method was used firstly by Zhou in 1986 to study electric circuits [17]. The differential transform is an iterative procedure based on the Taylor series expansion which constructs an analytic solution in the form of a polynomial. The method is well addressed in [18–23]. Recently, the generalized differential transform method is developed for obtaining approximate analytic solutions for some linear and nonlinear differential equations of fractional order [24, 25].

The Caputo fractional derivative is considered here because it allows traditional initial and boundary conditions to be included in the formulation of the problem.

2. Generalized Two-Dimensional Differential Transform Method (GDTM)

The fundamental theorems of the generalized two-dimensional differential transform are as follows.

Some details of the aformentioned theorems can be found in [30].

3. Applications of GDTM

3.1. Fractional Hirota-Satsuma Coupled KdV Equation

Consider the following time-fractional Hirota-Satsuma coupled KdV equation:

$$ (11)

subject to the initial conditions

$$ (12)

where c₀, c₂, β, and γ are arbitrary constants.

The exact solutions of (11) and (12), for the special case of α = 1, given in [26], are

$$ (13)

Suppose that the solutions u(x, t), v(x, t), and w(x, t) can be represented as the products of single-valued functions, respectively. Applying the generalized two-dimensional differential transform to both sides of (11) and using the related theorems, we have

$$ (14)

The generalized two-dimensional differential transforms of the initial conditions can be obtained as follows:

$$ (15)

Utilizing the recurrence relations (14) and the transformed initial conditions, we can obtain all the U_1,α(k, h), V_1,α(k, h), and W_1,α(k, h) with the help of Mathematica. Moreover, substituting all U_1,α(k, h) into (7), we obtain the series form solution

$$ (16)

where

$$ (17)

The closed forms of u₀(x, t), u₁(x, t), and u₂(x, t) are

$$ (18)

Similarly, substituting all V_1,α(k, h) and all W_1,α(k, h) into (7), respectively, we obtain the series form solutions

$$ (19)

The closed forms of v₀(x, t), v₁(x, t) and v₂(x, t) are

$$ (20)

The closed forms of w₀(x, t), w₁(x, t), and w₂(x, t) are

$$ (21)

The approximate solutions of (11) in finite series forms are given by

$$ (22)

$$ (23)

$$ (24)

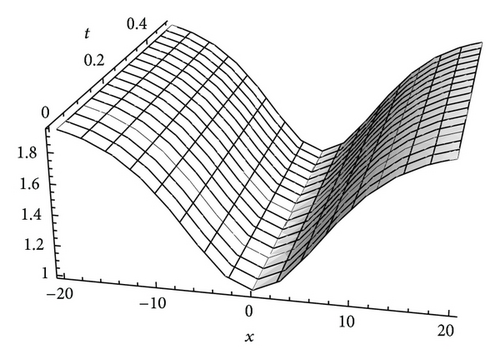
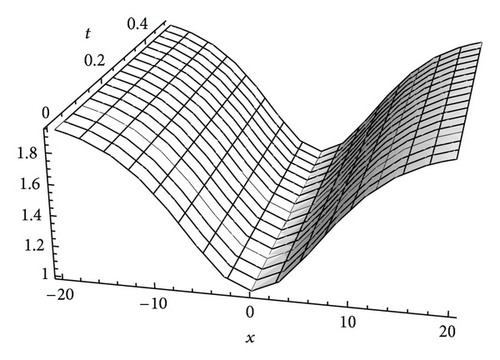
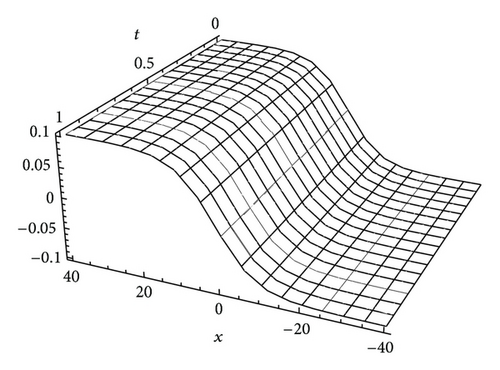
In order to verify whether the approximate solutions of (22)–(24) lead to higher accuracy, we draw the figures of the approximate solutions of (22)–(24) with α = 1, as well as the exact solutions (13) when c₀ = c₂ = 1, γ = 0.1, and β = 0.08. It can be seen from Figures 1(a) to 3(b) that the solutions obtained by the presented method is nearly identical with the exact solutions. So, we conclude that a good approximation is achieved by using the GDTM.

In the following, we will construct an approximate solution of (11) with the new initial conditions,

$$ (25)

where c₀, c₁, γ, and β are arbitrary constants.

The generalized two-dimensional differential transforms of the initial conditions of (25) are given by

$$ (26)

Utilizing the recurrence relations in (14) and the transformed initial conditions, we can obtain the following approximate solutions:

$$ (27)

where the closed forms of u_i(x, t), v_i(x, t), and w_i(x, t)  (i = 0,1, 2,3) are

$$ (28)

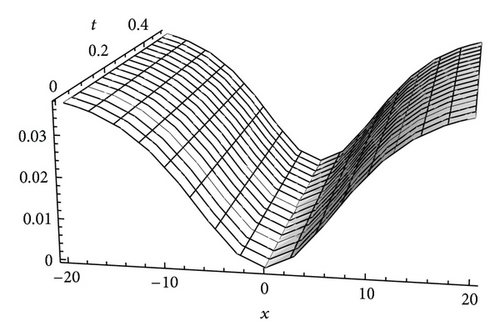
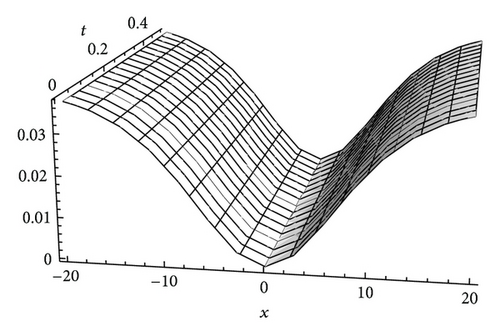
3.2. Fractional Coupled MKdV Equation

Consider the following time-fractional coupled MKdV equation:

$$ (29)

subject to the initial conditions

$$ (30)

where γ is an arbitrary constant.

The exact solutions of (29) and (30), for the special case of β = 1, given in [26], are

$$ (31)

Equation system of (29) is more complex. In order to obtain an explicit iteration scheme, we follow the pretreatment technique introduced recently by Chang [20, 21] to deal with long nonlinear items. Firstly, we suppose that

$$ (32)

According to (32), (29) can be equivalently written as the following form:

$$ (33)

Suppose that the solutions u(x, t) and v(x, t) can be represented as the products of single-valued functions, respectively. Applying the generalized two-dimensional differential transform to both sides of (33) and using the related theorems, we have

$$ (34)

Herein F_1,β(k, h),   G_1,β(k, h),   P_1,β(k, h), and Q_1,β(k, h) denote the differential transformations of the functions f(x, t), g(x, t), p(x, t), and q(x, t), respectively.

The generalized two-dimensional differential transforms of the initial conditions of (30) can be obtained as follows:

$$ (35)

Utilizing the recurrence relations of (34) and the transformed initial conditions, we can obtain all the U_1,β(k, h) and V_1,β(k, h) with the help of Mathematica. Through the complex calculation which is similar to the solving process in Section 3.1, we have the approximate solutions of (29) in finite series,

$$ (36)

$$ (37)

where the closed forms of u_i(x, t) and v_i(x, t)  (i = 0,1, 2,3) are given by

$$ (38)

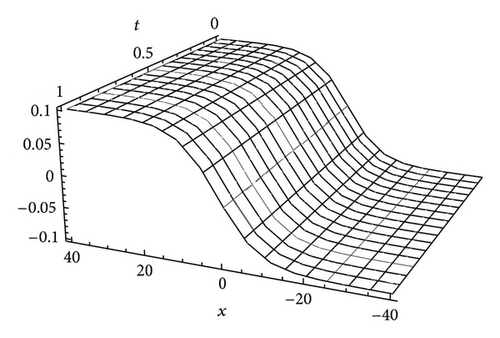
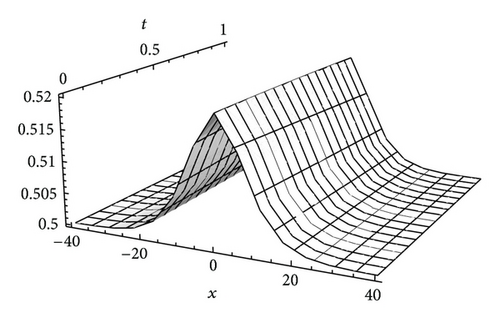
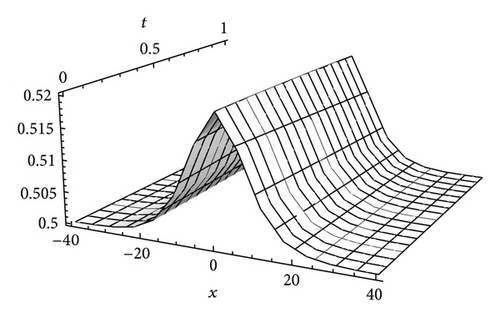
The effectiveness and accuracy of the approximate solutions can be seen from the comparison figures.

Figures 4 and 5 show the approximate solutions of (36) and (37) and the exact ones of (31) with α = λ = 1 and γ = 0.1, respectively. Comparing Figures 1(a) and 1(b) with Figures 2(a) and 2(b), we can see that the solutions obtained by different methods are nearly identical. From these figures, we can know that the series solutions converge rapidly, so a good approximation has been achieved.

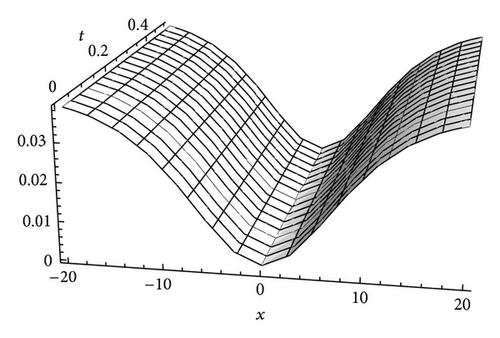
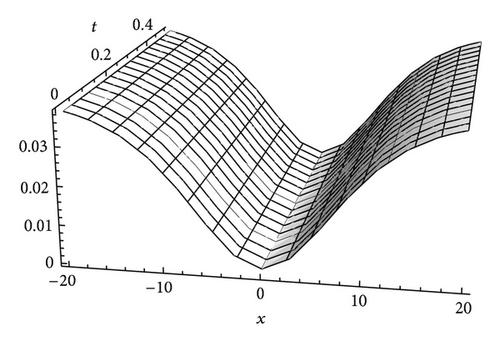
4. Summary and Discussion

In this paper, combining the Caputo fractional derivative, the GDTM was applied to derive approximate analytical solutions of the time-fractional Hirota-Satsuma coupled KdV equation and coupled MKdV equation with initial conditions. The numerical solutions obtained from the GDTM are shown graphically. The obtained results demonstrate the reliability of the algorithm and its wider applicability to nonlinear fractional coupled partial differential equations.

Setting u_m(x, t) = u_m(x)(t^mβ/Γ(1 + mβ)) and v_m(x, t) = v_m(x)(t^mβ/Γ(1 + mβ)), and using (43), we can obtain the 3-order approximate solutions as (36) and (37) by using the symbol computational software Mathematica.