Volume 2013, Issue 1 543549

Research Article

Open Access

Synchronization of Chaotic Delayed Fuzzy Neural Networks under Impulsive and Stochastic Perturbations

Bing Li,

Corresponding Author

Bing Li

[email protected]

College of Science, Chongqing Jiaotong University, Chongqing 400074, China cqjtu.edu.cn

Yangtze Center of Mathematics, Sichuan University, Chengdu 610064, China scu.edu.cn

Search for more papers by this author

Qiankun Song,

Qiankun Song

College of Science, Chongqing Jiaotong University, Chongqing 400074, China cqjtu.edu.cn

Search for more papers by this author

Bing Li,

Corresponding Author

Bing Li

[email protected]

College of Science, Chongqing Jiaotong University, Chongqing 400074, China cqjtu.edu.cn

Yangtze Center of Mathematics, Sichuan University, Chengdu 610064, China scu.edu.cn

Search for more papers by this author

Qiankun Song,

Qiankun Song

College of Science, Chongqing Jiaotong University, Chongqing 400074, China cqjtu.edu.cn

Search for more papers by this author

First published: 14 February 2013

https://doi.org/10.1155/2013/543549

Citations: 4

Academic Editor: Xiaodi Li

Share a link

Email
Wechat
Bluesky

Abstract

The synchronization problem of chaotic fuzzy cellular neural networks with mixed delays is investigated. By an impulsive integrodifferential inequality and the Itô′s formula, some sufficient criteria to synchronize the networks under both impulsive and stochastic perturbations are obtained. The example and simulations are given to demonstrate the efficiency and advantages of the proposed results.

1. Introduction

Fuzzy cellular neural network (FCNN), which integrated fuzzy logic into the structure of a traditional cellular neural networks (CNNs) and maintained local connectivity among cells, was first introduced by T. Yang and L. Yang [1] to deal with some complexity, uncertainty, or vagueness in CNNs. Lots of studies have illustrated that FCNNs are a useful paradigm for image processing and pattern recognition [2]. So far, many important results on stability analysis and state estimation of FCNNs have been reported (see [3–12] and the references therein).

Recently, it has been revealed that if the network’s parameters and time delays are appropriately chosen, then neural networks can exhibit some complicated dynamics and even chaotic behaviors [13, 14]. The chaotic system exhibits unpredictable and irregular dynamics, and it has been found in many fields. Since the drive-response concept was proposed by Pecora and Carroll [15] in 1990 for constructing the synchronization of coupled chaotic systems, the control and synchronization problems of chaotic systems have been extensively investigated. In recent years, various synchronization schemes for chaotic neural networks have derived and demonstrated potential applications in many areas such as secure communication, image processing and harmonic oscillation generation; see [16–32].

Although there have been many results which can be applied to synchronization problems of a broad class of FCNNs [25–32], there are some disadvantages that need attention.

(1) Synchronization procedures and schemes are rather sensitive to the unavoidable channel disturbances which are usually presented in two forms: impulse and random noise. However, in [25–27], authors provided some new schemes to synchronize the chaotic systems without considering both impulse and random noise. In [28, 29], under the condition of no channel disturbance, Yu et al. and Xing and Peng studied the lag synchronization problems of FCNNs, respectively. In [30, 31], authors studied the synchronization of impulsive fuzzy cellular neural networks (IFCNNs) with delays. In [32], authors derived some synchronization schemes for FCNNs with random noise. In fact, in real system, it is more reasonable that the two perturbations coexist simultaneously.

(2) The criteria proposed in [25–32] are valid only for FCNNs with discrete delays. For example, in [25, 28, 30, 31], the involved delays are constants. In [26, 27, 32], the involved delays are time-varying delays which are continuously differentiable, and the corresponding derivatives are required to be finite or not greater than 1. In [29], Xing and Peng provided some new criteria on lag synchronization problem of FCNNs but they only considered the case for bounded time-varying delays. In fact, time delays may occur in an irregular fashion, and sometimes they may be not continuously differentiable. Besides this, distribution delays may also exist when neural networks have a spatial extent due to the presence of a multitude of parallel pathways with a variety of axon sizes and lengths.

(3) Some conditions imposed on the impulsive perturbations are too strong. For instance, Feng et al. [31] required the magnitude of jumps not to be smaller than 0 and not greater than 2. However, the disturbance in the real environment may be very intense.

Therefore, it is of great theoretical and practical significance to investigate synchronization problems of IFCNNs with mixed delays and random noise. However, up to now, to the best of our knowledge, no result for synchronization of IFNNs with mixed delays and random noise has been reported.

Inspired by the above discussion, this paper addresses the exponential synchronization problem of IFCNNs with mixed delays and random noise. Based on the properties of nonsingular ℳ-matrix and the It’s formula, we design some synchronization schemes with a state feedback controller to ensure the exponential synchronization control. Our method does not resort to complicated Lyapunov-Krasovskii functional which is widely used. The proposed synchronization schemes are novel and improve some of the previous literature.

This paper is organized as follows. In Section 2, we introduce the drive-response models and some preliminaries. In Section 3, some synchronization criteria for FCNNs with mixed delays are derived. In Section 4, an example and its simulations are given to illustrate the effectiveness of theoretical results. Finally, conclusions are drawn in Section 5.

2. Model Description and Preliminaries

Let ℝⁿ be the space of n-dimensional real column vectors, and let ℝ^m×n represent the class of m × n matrices with real components. |·| denotes the Euclidean norm in ℝⁿ. The inequality “≤” (“>”) between matrices or vectors such as A ≤ B (A > B) means that each pair of corresponding elements of A and B satisfies the inequality “≤” (“>”). A ∈ ℝ^m×n is called a nonnegative matrix if A ≥ 0, and x ∈ ℝⁿ is called a positive vector if x > 0. The transpose of A ∈ ℝ^m×n or x ∈ ℝⁿ is denoted by A^T or x^T. Let E denote the unit matrix with appropriate dimensions. 𝒩 : = {1,2, …, n}, and ℕ : = {1,2, …}, ℝ₊ : = [0, +∞).

ℙℂ[J, ℝⁿ] = {ψ : J → ℝⁿ | ψ(s) is continuous and bounded for all but at most countable points s ∈ J and at these points, ψ(s⁺) and ψ(s⁻) exist, ψ(s) = ψ(s⁺)}. Here, J ⊂ ℝ is an interval; ψ(s⁺) and ψ(s⁻) denote the right-hand and left-hand limits of the function ψ(s), respectively. Especially ℙℂ : = ℙℂ[(−∞, 0], ℝⁿ] with the norm ∥ψ∥ = sup _−∞<s≤0 | ψ(s)| for ψ ∈ ℙℂ.

𝕃^e = {ψ : ℝ₊ → ℝ | ψ(s) is piecewise continuous and satisfies for some constant σ₀ > 0}.

For A, B ∈ ℝ^n×n and ϕ : ℝ → ℝⁿ, we denote that

()

and D⁺ϕ(t) denotes the upper-right derivative of ϕ(t) at time t.

Consider IFCNNs with mixed delays as follows:

()

where i = 1,2, …, n, n denotes the number of units in the neural network. x(t) = (x₁(t), …, x_n(t)) ^T represents the state variable. f_j(·) is the activation function of the jth neuron. c_i represents the passive decay rate to the state of ith neuron at time t. α_ij and γ_ij are elements of the fuzzy feedback MIN template. β_ij and θ_ij are elements of the fuzzy feedback MAX template. T_ij and S_ij are elements of fuzzy feed-forward MIN template and fuzzy feed-forward MAX template, respectively. a_ij and b_ij are elements of feedback and feed-forward template, respectively. ⋀ and ⋁ denote the fuzzy AND and fuzzy OR operations, respectively. ν_i and J_i denote input and bias of the ith neuron, respectively. For any i, j ∈ 𝒩, τ_ij(t) corresponding to the transmission delay satisfies 0 ≤ τ_ij(t) ≤ τ, and k_ij ∈ 𝕃^e is the feedback kernel. For any k ∈ ℕ, I_k(·) represents the impulsive perturbation, and t_k denotes impulsive moment satisfying t_k < t_k+1, lim _k→+∞t_k = +∞.

We make the following assumptions throughout this paper.

(A₁) f_i is globally Lipschitz continuous, that is, for any i ∈ 𝒩, there exists nonnegative constant L_i such that
()
(A₂) For any k ∈ ℕ, there is a nonnegative constant η_k such that
()

Let (2) be the drive system, and let the response system with random noise be described by

()

where w(t) = (w₁(t), …, w_n(t)) ^T is an n-dimensional standard Brownian motion defined on a complete probability space (Ω, ℱ, 𝒫) with a natural filtration {ℱ_t} _t≥0 generated by {w(s) : 0 ≤ s ≤ t} and satisfying the usual conditions (i.e., it is right continuous, and ℱ₀ contains all 𝒫-null sets). The initial value

which denotes the family of all bounded ℱ₀-measurable and ℙℂ-valued random variables ψ with the norm

, where E denotes the expectation of stochastic process. U(t) = (U₁(t), …, U_n(t)) ^T is the state feedback controller designed by

()

where M = (M_ij) _n×n, N = (N_ij) _n×n are the controller gain matrices to be scheduled. The diffusion coefficient matrix (or noise intensity matrix) σ : ℝ × ℝⁿ × ℝⁿ → ℝ^n×n satisfies the local Lipschitz condition and the linear growth condition (see [33]). In addition,

(A₃) for i ∈ 𝒩, there exist nonnegative constants c_ij, d_ij such that
()

where σ_i = (σ_i1, …, σ_in).

Let e(t) = (e₁(t), …, e_n(t)) ^T, where e_i(t) = y_i(t) − x_i(t), be the synchronization error. Then, the error dynamical system between (2) and (5) is given by

()

For convenience, we use the following notations: D₁ = diag {−c₁, …, −c_n}, L = diag {L₁, …, L_n}, K(s) = (k_ij(s)) _n×n, A = (a_ij) _n×n, with , for i ≠ j, α = (α_ij) _n×n, β = (β_ij) _n×n, Γ = (γ_ij) _n×n, Θ = (θ_ij) _n×n, C = (c_ij) _n×n, and D = (d_ij) _n×n.

The following definition and lemmas will be employed.

Definition 1. The systems (2) and (5) are called to be globally exponentially synchronized in p-moment, if there exist positive constants λ, K such that

()

It is said especially to be globally exponentially synchronized in mean square when p = 2.

For any nonsingular ℳ-matrix A (see [34]), we define that

()

Lemma 2 (see [35].)For a nonsingular ℳ-matrix A, ℳ_A is a nonempty cone without conical surface.

Lemma 3 (see [36].)For x_i ≥ 0, α_i > 0, and ,

()

The sign of equality holds if and only if x_i = x_j for all i, j ∈ 𝒩.

Lemma 4 (see [1].)Let α_ij, β_ij ∈ ℝ and x, y ∈ ℝⁿ be the two states of the system (2). Then, one has

()

Lemma 5 (see [36].)For the integer p ≥ 2 and x = (x₁, …, x_n) ^T ∈ ℝⁿ, there exists a positive constant e_p(n) such that

()

Lemma 6. For k ∈ ℕ, assume that v = (v₁(t), …, v_n(t)) ^T ∈ ℙℂ[(−∞, +∞), ℝⁿ] satisfies

()

in which

(C₁) A₀ = diag {a₁, …, a_n}, P = (p_ij) _n×n with p_ij ≥ 0 for i ≠ j, Q = (q_ij) _n×n ≥ 0, Υ(s) = (υ_ij(s)) _n×n ≥ 0, and υ_ij ∈ 𝕃^e, i, j ∈ 𝒩.
(C₂) is a nonsingular ℳ-matrix.

Then, there must exist z = (z₁, …, z_n) ^T ∈ ℳ_Π and λ ∈ (0, σ₀] such that

()

provided that the initial value

satisfies

()

where ϱ₀ = 1, ϱ_k = max {1, ρ_k}, and z, λ can be determined by

()

Proof. By condition (C₂) and Lemma 2, we can find such that , namely, . By the continuity, there must be some positive constant λ ∈ (0, σ₀] satisfying

()

Noting that

, we can find a constant B > 0 such that

. Denote that

. Obviously, z and λ satisfy (16) and (17).

Let for t ∈ ℝ, i ∈ 𝒩. For any small enough ϵ > 0, (16) implies that v_i(t) ≤ w_i(t)<(1 + ϵ)w_i(t), t ∈ (−∞, t₀]. Next, we claim that for any t ∈ [t₀, t₁),

()

If inequality (19) is not true, then there must exist some m ∈ 𝒩 and t^* ∈ (t₀, t₁) such that

()

On the other hand, (14) together with (17) and (20) leads to

()

which contradicts (21). Therefore, (19) holds. Letting ϵ → 0⁺ in (19), we get

()

Suppose that for ν = 1,2, …, k, the following inequalities hold

()

For t = t_k, from (14) and (24), we have

()

Recalling ρ_k ≥ 1, it follows from (24) and (25) that

()

Repeating the proof similar to (19) can yield

()

By the mathematical induction, we derive that for any k ∈ ℕ,

()

The proof is completed.

3. Exponential Synchronization

In this section, by using Lemma 6, we will obtain some sufficient criteria to synchronize the drive-response systems (2) and (5).

Theorem 7. Assume that (A₁)–(A₃) hold and

(A₄) for p ≥ 2, is a nonsingular ℳ-matrix, where , , , D₀ = diag {d₁, …, d_n} with
()
(A₅) the impulsive perturbations satisfy
()

where

, and λ ∈ (0, σ₀] is determined by

()

Then, drive-response systems (2) and (5) are globally exponential synchronization in p-moment.

Proof. Since is a nonsingular ℳ-matrix, by Lemma 2 and the continuity, there must be a constant vector and a constant λ ∈ (0, σ₀] such that (31) holds.

We denote by e = (e₁, …, e_n) ^T the solution of error dynamical system (8) with the initial value and let

()

Calculating the time derivative of V_i(e(t)) along the trajectory of error system (8) and by the Itô’s formula [33], we get for any k ∈ ℕ,

()

where ℒV_i(e(t)) is given by

()

By (A₁) and Lemma 4, we have

()

Using Lemma 3 and (A₃), it is easy to get

()

Thus, we have

()

It follows from (A₄) and (32) that

()

Substituting (38) into (33) gives

()

Integrating and taking the expectations on both sides of (39) lead to

()

where δ > 0 is small enough such that t, t + δ ∈ [t_k−1, t_k) for k ∈ ℕ.

By the continuity of EV_i(e(t)), we conclude that

()

which implies that for t ≠ t_k, k ∈ ℕ,

()

Meanwhile, it follows from (A₂) and (32) that

()

for i ∈ 𝒩 and k ∈ ℕ, which means that

()

Obviously, (42) and (44) indicate that EV(e(t)) satisfies inequality (14) in Lemma 6.

On the other hand, noting that e(t₀ + s) = ψ(s) − ϕ(s) in (8) and by a simple calculation, we get

()

for any s ∈ (−∞, 0], which means

for t ∈ (−∞, t₀] and i ∈ 𝒩. Recalling the definition of V(e(t)) in (32) and z > 0, we conclude that for t ∈ (−∞, t₀]

()

which further indicates that

()

where

. This implies that condition (16) in Lemma 6 holds.

Therefore, by Lemma 6, we derive that

()

with ζ₀ = 1. Meanwhile, (30) implies that there is a small enough constant ϵ (0 < ϵ < λ) such that

()

Thus, inequality (48) together with (49) shows that for k = 1

()

and for any k ≥ 2,

()

By Lemma 5, we get

()

where

. The proof is complete.

Remark 8. In [25–32], the authors established some useful criteria for ensuring synchronization of FCNNs with delays, respectively. However, once the unbounded distributed delays are involved, all results in [25–32] will be invalid. Hence, in this sense, the proposed Theorem 7 has a wider range of applications than those in previous papers.

Remark 9. In synchronization scheme, we take both impulsive perturbations and random noise into account. Comparing with the results in [25–32], Theorem 7 can reflect a more realistic dynamical behavior and synchronization procedure.

If the random noise has not been considered, which means σ ≡ 0 in (5), then the response system reduces to

()

In this case, the following globally exponential synchronization scheme for drive-response IFCNNs (2) and (53) can be derived.

Theorem 10. Assume that (A₁) and (A₂) hold and

(A₆) is a nonsingular ℳ-matrix, where , ,
(A₇) the impulsive perturbations satisfy
()

where ξ_k = max {1, η_k}, and λ ∈ (0, σ₀] is determined by

()

Then, the drive-response systems (2) and (53) are globally exponential synchronization.

Proof. Let V(e(t)) = [e(t)] ⁺ = (|e₁(t)|, …, |e_n(t) | ) ^T. Calculating the time derivative of V(e(t)) along with the trajectory of error system can give

()

The rest proof is similar to Theorem 7 and omitted here. We complete the proof.

Remark 11. In [31], Feng et al. derived some criteria on the globally exponential synchronization for a special case of (2) and (53) with γ_ij = θ_ij = 0, τ_ij(t) = τ_ij and for i, j ∈ 𝒩, k ∈ ℕ. In order to achieve synchronous control, the conditions as 0 ≤ η_ik ≤ 2 for i ∈ 𝒩, k ∈ ℕ have been imposed on the impulsive perturbations. However, Theorem 10 drops these restrictions.

4. Illustrative Example

In this section, a numerical example and its simulations are given to illustrate the effectiveness of our results.

Example 1. Consider the following 2-dimensional IFCNNs with mixed delays as the drive system

()

where i, j = 1,2, f_j(u) = tanh(u). J_k = e^0.15 + 1, t_k = t_k−1 + 4 for k ∈ ℕ. For the simplicity of computer simulations, we choose k_ij(s) = e^−s for s ∈ [0,20], k_ij(s) = 0 for s ∈ [20, +∞). The system parameters are as follows:

()

We can choose σ₀ = 0.8 and L₁ = L₂ = 1 such that k_ij ∈ 𝕃^e and (A₁) holds, respectively. Obviously, (A₂) holds with η_k = e^0.15, k ∈ ℕ.

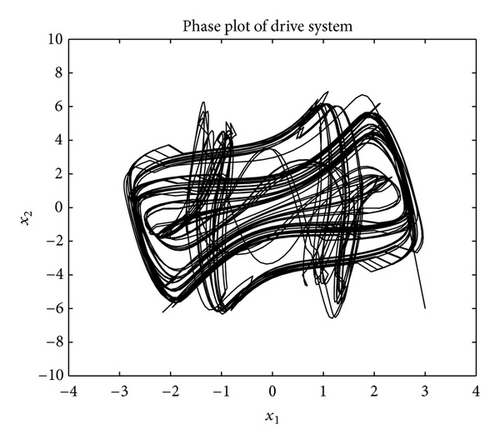
Choosing the initial value ϕ(s) = (3, −6) ^T for s ∈ (−∞, 0], the drive system (57) possesses a chaotic behavior as shown in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Chaos behavior of drive system.

Case 1. The response system without random noise is given by

()

The control gain matrices M and N can be chosen as

()

By simple calculation, we get that

()

is a nonsingular ℳ-matrix, which implies that (A₆) holds. Moreover, we can choose λ = 0.2 and

such that (A₇) holds. Therefore, by Theorem 10, the drive-response systems (57) and (59) are globally exponentially synchronized. The simulation result with ψ(s) = (1.3,1.8) ^T is shown in Figure 2.

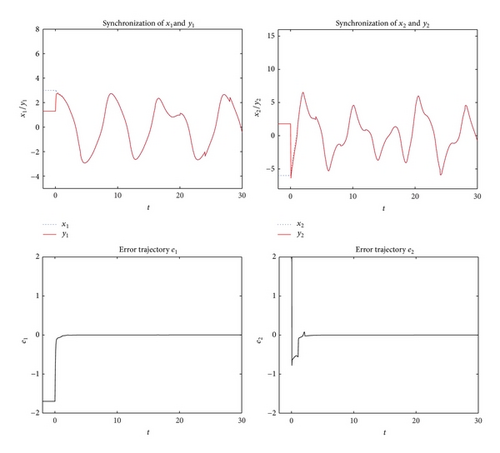
Remark 12. It is worth noting that the impulsive perturbations J_k > 2, which are not a satisfied condition (H2) in [31]. That is to say, even in the absence of the unbounded distributed delays, the results in [31] still cannot be applied to the synchronization problem of (57) and (59).

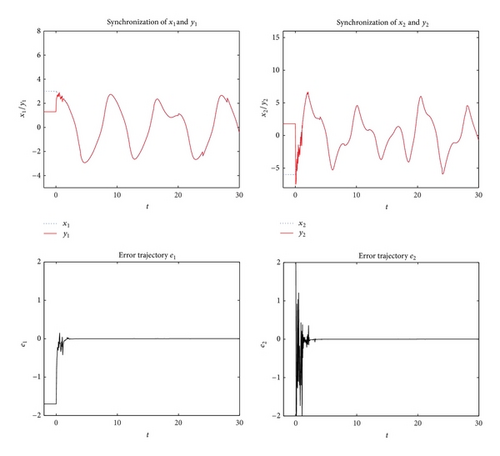
Case 2. Consider the response system with random noise as follows:

()

and the noise intensity matrix is

()

Clearly, we can choose

()

such that (A₃) holds.

For p = 2, let control gain matrices be

()

It is easy to deduce that

()

is a nonsingular ℳ-matrix, which implies that (A₄) holds. Meanwhile, we can choose λ = 0.1 and

such that (A₅) holds. Hence, by Theorem 7, the drive-response systems (57) and (62) are globally exponentially synchronized in mean square. The simulation result based on Euler-Maruyama method is illustrated in Figure 3.

Remark 13. The schemes proposed in [25–29] cannot solve the synchronization problem of (57) and (62) due to the impulsive perturbations and random noise. Besides this, the distributed delays make those methods in [30–32] cannot be applied to synchronization problem of (57) and (62).

5. Conclusion

In this paper, we investigate the synchronization problem of IFCNNs with mixed delays. Based on the properties of nonsingularℳ-matrix and some stochastic analysis approaches, some useful synchronization criteria under both impulse and random noise are obtained. The methods used in this paper are novel and can be extended to many other types of neural networks. These problems will be considered in near future.

Acknowledgments

The authors thank the editor and reviewers for their useful comments. This work was supported by the National Natural Science Foundation of China under Grants 11271270 and 61273021 and the Natural Science Foundation Project of CQ CSTC 2011jjA00012.

References

1 Yang T. and Yang L., The global stability of fuzzy cellular neural network, IEEE Transactions on Circuits and Systems I. (1996) 43, no. 10, 880–883, https://doi.org/10.1109/81.538999, MR1416906.
10.1109/81.538999
Web of Science® Google Scholar
2 Yang T. and Yang L., Fuzzy cellular neural network: a new paradigm for image processing, International Journal of Circuit Theory and Applications. (1997) 25, no. 6, 469–481, 2-s2.0-0031268281.
10.1002/(SICI)1097-007X(199711/12)25:6<469::AID-CTA967>3.0.CO;2-1
Web of Science® Google Scholar
3 Liu Y. and Tang W., Exponential stability of fuzzy cellular neural networks with constant and time-varying delays, Physics Letters A. (2004) 323, no. 3-4, 224–233, https://doi.org/10.1016/j.physleta.2004.01.064, MR2050486, ZBL1118.81400.
10.1016/j.physleta.2004.01.064
CAS Web of Science® Google Scholar
4 Huang T., Exponential stability of delayed fuzzy cellular neural networks with diffusion, Chaos, Solitons & Fractals. (2007) 31, no. 3, 658–664, https://doi.org/10.1016/j.chaos.2005.10.015, MR2262300, ZBL1138.35414.
10.1016/j.chaos.2005.10.015
Web of Science® Google Scholar
5 Niu S., Jiang H., and Teng Z., Exponential stability and periodic solutions of FCNNs with variable coefficients and time-varying delays, Neurocomputing. (2008) 71, no. 13–15, 2929–2936, 2-s2.0-55549095381, https://doi.org/10.1016/j.neucom.2007.07.004.
10.1016/j.neucom.2007.07.004
Web of Science® Google Scholar
6 Chen L. and Zhao H., Stability analysis of stochastic fuzzy cellular neural networks with delays, Neurocomputing. (2008) 72, no. 1–3, 436–444, 2-s2.0-55949088751, https://doi.org/10.1016/j.neucom.2007.12.005.
10.1016/j.neucom.2007.12.005
Web of Science® Google Scholar
7 Zhao H., Ding N., and Chen L., Almost sure exponential stability of stochastic fuzzy cellular neural networks with delays, Chaos, Solitons & Fractals. (2009) 40, no. 4, 1653–1659, https://doi.org/10.1016/j.chaos.2007.09.044, MR2531255, ZBL1198.34173.
10.1016/j.chaos.2007.09.044
Web of Science® Google Scholar
8 Wang X. and Xu D., Global exponential stability of impulsive fuzzy cellular neural networks with mixed delays and reaction-diffusion terms, Chaos, Solitons & Fractals. (2009) 42, no. 5, 2713–2721, https://doi.org/10.1016/j.chaos.2009.03.177, MR2559991, ZBL1198.34094.
10.1016/j.chaos.2009.03.177
Web of Science® Google Scholar
9 Li X., Rakkiyappan R., and Balasubramaniam P., Existence and global stability analysis of equilibrium of fuzzy cellular neural networks with time delay in the leakage term under impulsive perturbations, Journal of the Franklin Institute. (2011) 348, no. 2, 135–155, https://doi.org/10.1016/j.jfranklin.2010.10.009, MR2771833, ZBL1241.92006.
10.1016/j.jfranklin.2010.10.009
Web of Science® Google Scholar
10 Balasubramaniam P., Kalpana M., and Rakkiyappan R., Global asymptotic stability of BAM fuzzy cellular neural networks with time delay in the leakage term, discrete and unbounded distributed delays, Mathematical and Computer Modelling. (2011) 53, no. 5-6, 839–853, https://doi.org/10.1016/j.mcm.2010.10.021, MR2769457, ZBL1217.34116.
10.1016/j.mcm.2010.10.021
Web of Science® Google Scholar
11 Syed A. M. and Balasubramaniam P., Global asymptotic stability of stochastic fuzzy cellular neural networks with multiple discrete and distributed time-varying delays, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 7, 2907–2916, https://doi.org/10.1016/j.cnsns.2010.10.011, MR2772305, ZBL1221.34189.
10.1016/j.cnsns.2010.10.011
Web of Science® Google Scholar
12 Balasubramaniam P., Kalpana M., and Rakkiyappan R., State estimation for fuzzy cellular neural networks with time delay in the leakage term, discrete and unbounded distributed delays, Computers & Mathematics with Applications. (2011) 62, no. 10, 3959–3972, https://doi.org/10.1016/j.camwa.2011.09.048, MR2852113, ZBL1236.93004.
10.1016/j.camwa.2011.09.048
Web of Science® Google Scholar
13 Zou F. and Nossek J., Bifurcation and chaos in cellular neural networks, IEEE Transactions on Circuits and Systems I. (1993) 40, no. 3, 166–173, https://doi.org/10.1109/81.222797, MR1232559, ZBL0782.92003.
10.1109/81.222797
Web of Science® Google Scholar
14 Lu H., Chaotic attractors in delayed neural networks, Physics Letters A. (2002) 298, no. 2-3, 109–116, 2-s2.0-0037013883, https://doi.org/10.1016/S0375-9601(02)00538-8.
10.1016/S0375-9601(02)00538-8
CAS Web of Science® Google Scholar
15 Pecora L. M. and Carroll T. L., Synchronization in chaotic systems, Physical Review Letters. (1990) 64, no. 8, 821–824, https://doi.org/10.1103/PhysRevLett.64.821, MR1038263, ZBL0938.37019.
10.1103/PhysRevLett.64.821
CAS PubMed Web of Science® Google Scholar
16 Liao T. L. and Tsai S. H., Adaptive synchronization of chaotic systems and its application to secure communications, Chaos, Solitons & Fractals. (2000) 11, no. 9, 1387–1396, 2-s2.0-0034217050, https://doi.org/10.1016/S0960-0779(99)00051-X.
10.1016/S0960-0779(99)00051-X
Web of Science® Google Scholar
17 Barahona M. and Pecora L. M., Synchronization in small-world systems, Physical Review Letters. (2002) 89, no. 5, article 054101, 2-s2.0-3343010976.
10.1103/PhysRevLett.89.054101
PubMed Web of Science® Google Scholar
18 Cao J., Wang Z., and Sun Y., Synchronization in an array of linearly stochastically coupled networks with time delays, Physica A. (2007) 385, no. 2, 718–728, https://doi.org/10.1016/j.physa.2007.06.043, MR2584887.
10.1016/j.physa.2007.06.043
Web of Science® Google Scholar
19 Yu W. and Cao J., Synchronization control of stochastic delayed neural networks, Physica A. (2007) 373, 252–260, 2-s2.0-33750445571, https://doi.org/10.1016/j.physa.2006.04.105.
10.1016/j.physa.2006.04.105
Web of Science® Google Scholar
20 Zhu W., Xu D., and Huang Y., Global impulsive exponential synchronization of time-delayed coupled chaotic systems, Chaos, Solitons & Fractals. (2008) 35, no. 5, 904–912, 2-s2.0-35248872134, https://doi.org/10.1016/j.chaos.2006.05.078.
10.1016/j.chaos.2006.05.078
Web of Science® Google Scholar
21 Song Q., Synchronization analysis of coupled connected neural networks with mixed time delays, Neurocomputing. (2009) 72, no. 16–18, 3907–3914, 2-s2.0-69249235736, https://doi.org/10.1016/j.neucom.2009.04.009.
10.1016/j.neucom.2009.04.009
Web of Science® Google Scholar
22 Li T., Song A., Fei S., and Guo Y., Synchronization control of chaotic neural networks with time-varying and distributed delays, Nonlinear Analysis. (2009) 71, no. 5-6, 2372–2384, https://doi.org/10.1016/j.na.2009.01.079, MR2524444, ZBL1171.34049.
10.1016/j.na.2009.01.079
Web of Science® Google Scholar
23 Li X. and Fu X., Synchronization of chaotic delayed neural networks with impulsive and stochastic perturbations, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 2, 885–894, https://doi.org/10.1016/j.cnsns.2010.05.025, MR2725812, ZBL1221.93225.
10.1016/j.cnsns.2010.05.025
Web of Science® Google Scholar
24 Yang X., Huang C., and Zhu Q., Synchronization of switched neural networks with mixed delays via impulsive control, Chaos, Solitons & Fractals. (2011) 44, no. 10, 817–826, https://doi.org/10.1016/j.chaos.2011.06.006, MR2837280.
10.1016/j.chaos.2011.06.006
Web of Science® Google Scholar
25 Ding W. and Han M., Synchronization of delayed fuzzy cellular neural networks based on adaptive control, Physics Letters A. (2008) 372, no. 26, 4674–4681, 2-s2.0-44449094700, https://doi.org/10.1016/j.physleta.2008.04.053.
10.1016/j.physleta.2008.04.053
CAS Web of Science® Google Scholar
26 Xia Y., Yang Z., and Han M., Synchronization schemes for coupled identical Yang-Yang type fuzzy cellular neural networks, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 9-10, 3645–3659, https://doi.org/10.1016/j.cnsns.2009.01.028, MR2509952, ZBL1221.37227.
10.1016/j.cnsns.2009.01.028
Web of Science® Google Scholar
27 Wang L., Ding W., and Chen D., Synchronization schemes of a class of fuzzy cellular neural networks based on adaptive control, Physics Letters A. (2010) 374, no. 13-14, 1440–1449, 2-s2.0-77649232667, https://doi.org/10.1016/j.physleta.2010.01.029.
10.1016/j.physleta.2010.01.029
CAS Web of Science® Google Scholar
28 Yu J., Hu C., Jiang H., and Teng Z., Exponential lag synchronization for delayed fuzzy cellular neural networks via periodically intermittent control, Mathematics and Computers in Simulation. (2012) 82, no. 5, 895–908, https://doi.org/10.1016/j.matcom.2011.11.006, MR2892129, ZBL1244.65097.
10.1016/j.matcom.2011.11.006
Web of Science® Google Scholar
29 Xing Z. and Peng J., Exponential lag synchronization of fuzzy cellular neural networks with time-varying delays, Journal of the Franklin Institute. (2012) 349, no. 3, 1074–1086, https://doi.org/10.1016/j.jfranklin.2011.12.008, MR2899327.
10.1016/j.jfranklin.2011.12.008
Web of Science® Google Scholar
30 Ding W., Synchronization of delayed fuzzy cellular neural networks with impulsive effects, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 11, 3945–3952, https://doi.org/10.1016/j.cnsns.2009.02.013, MR2522897, ZBL1221.34194.
10.1016/j.cnsns.2009.02.013
Web of Science® Google Scholar
31 Feng X., Zhang F., and Wang W., Global exponential synchronization of delayed fuzzy cellular neural networks with impulsive effects, Chaos, Solitons & Fractals. (2011) 44, no. 1–3, 9–16, https://doi.org/10.1016/j.chaos.2010.10.003, MR2782489, ZBL1230.93049.
10.1016/j.chaos.2010.10.003
Web of Science® Google Scholar
32 Gan Q., Xu R., and Yang P., Exponential synchronization of stochastic fuzzy cellular neural networks with time delay in the leakage term and reaction-diffusion, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 4, 1862–1870, https://doi.org/10.1016/j.cnsns.2011.08.029, MR2855476, ZBL1239.93110.
10.1016/j.cnsns.2011.08.029
Web of Science® Google Scholar
33 Friedman A., Stochastic Differential Equations and Applications, 1975, Academic Press, NewYork, NY, USA.
Google Scholar
34 Horn R. A. and Johnson C. R., Matrix Analysis, 1985, Cambridge University Press, Cambridge, UK, MR832183.
10.1017/CBO9780511810817
Google Scholar
35 Yang Z. and Xu D., Robust stability of uncertain impulsive control systems with time-varying delay, Computers & Mathematics with Applications. (2007) 53, no. 5, 760–769, https://doi.org/10.1016/j.camwa.2006.10.023, MR2327632, ZBL1133.93362.
10.1016/j.camwa.2006.10.023
Web of Science® Google Scholar
36 Yang Z., Xu D., and Xiang L., Exponential p-stability of impulsive stochastic differential equations with delays, Physics Letters A. (2006) 359, no. 2, 129–137, https://doi.org/10.1016/j.physleta.2006.05.090, MR2253515.
10.1016/j.physleta.2006.05.090
CAS Web of Science® Google Scholar

All articles

Synchronization of Chaotic Delayed Fuzzy Neural Networks under Impulsive and Stochastic Perturbations

Abstract

1. Introduction

2. Model Description and Preliminaries

3. Exponential Synchronization

4. Illustrative Example

5. Conclusion

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Synchronization of Chaotic Delayed Fuzzy Neural Networks under Impulsive and Stochastic Perturbations

Abstract

1. Introduction

2. Model Description and Preliminaries

3. Exponential Synchronization

4. Illustrative Example

5. Conclusion

Acknowledgments

References

Figures

References

Related

Information