Synchronization of complex networks has been extensively studied in many fields, where intensive efforts have been devoted to the understanding of its mechanisms. As for discriminating network synchronizability by Master Stability Function method, a dilemma usually encountered is that we have no prior knowledge of the network type that the synchronous region belongs to. In this paper, we investigate a sufficient condition for a general complex dynamical network in the absence of control. A main result is that, when the coupling strength is sufficiently strong, the dynamical network achieves synchronization provided that the symmetric part of the inner-coupling matrix is positive definite. According to our results, synchronous region of the network with positive definite inner-coupling matrix belongs to the unbounded one, and then the eigenvalue of the outer-coupling matrix nearest 0 can be used for judging synchronizability. Even though we cannot gain the necessary and sufficient conditions for synchronizing a network so far, our results constitute a first step toward a better understanding of network synchronization.

1. Introduction

Complex dynamical networks have received increasing attention from different fields in the past two decades. So far, the dynamics of complex networks has been extensively investigated, in which synchronization is a typical topic which has attracted lots of concern [1–17].

As an interesting phenomenon that enables coherent behavior in networks as a result of coupling, synchronization and the discussion upon its sufficient or necessary condition are fundamental and valuable. Pecora and his colleagues used the so-called Master Stability Function (MSF) approach to determine the synchronous region in coupled systems [18, 19], in which the negativeness of Lyapunov Exponent for master stability equation ensures synchronization. Combining MSF approach with Gershörin disk theory, Chen et al. imposed constraints on the coupling strengths to guarantee stability of the synchronous states in coupled dynamical network [20]. These methods, however, obtain just necessary conditions for synchronization due to the fact that Lyapunov Exponent is employed to judge the stability of system.

Zhou et al. and Li and Chen investigated synchronization in general dynamical networks by integrating network models and an adaptive technique and proved that strong enough couplings will synchronize an array of identical cells [11, 12]. To overcome the difficulties caused by too many controllers in large scale complex networks, pinning mechanism is further applied to analyze network synchronization criteria in the works by Zhou et al. and Chen et al. [13, 14]. Research studies on network synchronization mentioned above focused on sufficient conditions, but all of them are gained by introducing controllers.

For general complex dynamical networks in the absence of control, we investigate their sufficient conditions for achieving network synchronization in the current work. Using Lyapunov direct method [21, 22] and matrix theory [23–27], a criterion for synchronization in generally coupled identical systems is proposed. We conclude that network synchronization will be reached when the coupling strength is larger than a threshold, given that the symmetric part of the inner-coupling matrix is positive definite. It is analytically derived in our paper that a network belongs to Type I with respect to synchronized region [28], provided with a positive definite inner-coupling matrix.

For discriminating network synchronizability, it is well known that a dilemma is usually encountered in the process of applying MSF method. That is, we have no prior knowledge of the network type that the synchronous region belongs to. Stemmed from our results, the eigenvalue of the outer-coupling matrix nearest 0 can be used for judging synchronizability of a dynamical network with positive definite inner-coupling matrix. Even though we cannot gain the necessary and sufficient conditions for synchronizing a network so far, our results constitute a first step toward a better understanding of network synchronization.

The rest of the paper is organized as follows. In Section 2, a general complex dynamical network model and some mathematical preliminaries are introduced. A sufficient condition for achieving synchronization in the network and detailed discussion are presented in Section 3. Section 4 gives some numerical simulations to show the effectiveness of the proposed synchronization criterion and further illustrates the relationship between synchronous region and our main results. Conclusions are finally drawn in Section 5.

2. Preliminaries

To begin with, we introduce a complex network model describing the dynamical evolution of node states, which is formulated as

()

where 1 ≤ i ≤ N, 𝒩_i represents the neighborhood of the ith node, the state vector of the ith node x_i(t) = (x_i1(t), x_i2(t), …, x_in(t)) ^⊤ ∈ ℝⁿ is a continuous function, f : ℝⁿ → ℝⁿ is a smooth nonlinear vector function, individual node dynamics is

, and H ∈ ℝ^{n × n} is the inner-coupling matrix. The outer-coupling weight configuration matrix A = (a_ij) ∈ ℝ^{N × N} (a_ij ∈ {0,1}, j ≠ i) is symmetric and diffusive satisfying

. If there is a link between node i and node j (j ≠ i), then a_ij = a_ji = 1; otherwise, a_ij = a_ji = 0. In addition,

. It is clear that 0 = λ₁ > λ₂ ≥ λ₃ ≥ ⋯≥λ_N due to the diffusion, with λ_i (1 ≤ i ≤ N) being the eigenvalues of A.

Definition 1. Let be a solution of the complex dynamical network (1) with initial state . Assume that f : Ω → Rⁿ is continuously differentiable, where Ω⊆Rⁿ. If there is a nonempty subset E⊆Ω, with x_i(t₀) ∈ E (1 ≤ i ≤ N), such that x_i(X₀; t) ∈ Ω for all t ≥ t₀, 1 ≤ i ≤ N and that

()

where ∥·∥ denotes any norm of a vector or a matrix, then the complex dynamical network (1) is said to achieve synchronization.

To develop the main results, a useful hypothesis on the inner-coupling matrix H is introduced.

Assumption 2. Suppose that μ_i > 0 (1 ≤ i ≤ n), with μ₁, μ₂, …, μ_n being eigenvalues of the symmetric part of the inner-coupling matrix H^s≜(H + H^⊤)/2.

It suggests that H^s should be a positive definite matrix. This is common for the inner-coupling matrix H to satisfy μ_i > 0 (1 ≤ i ≤ n); for instance, the symmetric part H^s is strictly diagonally dominant.

Since A and H^s are symmetric, there exist orthogonal matrices P ∈ ℝ^N×N and Q ∈ ℝ^n×n, such that

()

where λ₁, λ₂, …, λ_N are real numbers and the denotation diag {*, **, …, ***} represents a diagonal matrix whose elements are *, **, …, ***.

Let ξ = (ξ₁, ξ₂, …, ξ_N) ^⊤ be the left eigenvector of the coupling configuration matrix A corresponding to the eigenvalue λ₁ = 0, in which . It is obvious that ξ^⊤A = 0. Then introducing a weighted mean state of all nodes

()

one has the following Lemma.

Lemma 3. For any initial state X₀ of model (1), network synchronization lim _t→∞ ∥x_i(t) − x_j(t)∥ = 0 (1 ≤ i, j ≤ N) is equivalent to .

Proof. On one hand, provided with lim _t→∞∥x_i(t) − x_j(t)∥ = 0 (1 ≤ i, j ≤ N), one obtains

()

Thus lim _t→∞∥x_i(t) − x_j(t)∥ = 0 (1 ≤ i, j ≤ N) results in

On the other hand, if , one has . Owing to the fact that

()

one gets lim _t→∞∥x_i(t) − x_j(t)∥ = 0 (1 ≤ i, j ≤ N).

Remark 4. Lemma 3 has proved that is a sufficient and necessary condition for network synchronization. In other words, the dynamics of all nodes in the complex network (1) would approach when network synchronization is reached.

Recently, it has been mathematically proved that is a solution of single node dynamical system in the sense of positive limit set [29]

()

Namely, the synchronous state can be an equilibrium point, a periodic orbit, an aperiodic orbit, or even a chaotic orbit in the phase space.

Define the state error vectors as for all nodes in the network.

Then the error system is given by

()

according to systems (1) and (4), where 1 ≤ i ≤ N.

Denote , , F(X) = (f(x₁) ^⊤, f(x₂) ^⊤, …, f(x_N) ^⊤) ^⊤, and . Then one has

()

where ⊗ represents the direct product of matrices.

3. Main Results

In this section, a sufficient condition for reaching synchronization in a general complex dynamical network (1) is presented based on Lyapunov direct method and some related matrix theory. Further discussion of the synchronization criterion in detail is also included.

Linearizing the state equation (1) at trajectory

, one obtains the variational equation as follows:

()

where

is the Jacobian matrix of

evaluated at trajectory

. Letting

, one has

()

Denote η as the form

, where η_i = (η_i1, η_i2, …, η_in) ^⊤ ∈ ℝⁿ. Equation (11) can be rewritten as follows:

()

where 1 ≤ i ≤ N.

For λ₁ = 0 (i = 1), one gets the variational equation for the synchronization manifold. Thus one has succeeded in separating i = 1 from the transverse directions i = 2, 3, …, N. All the i = 2, 3, …, N correspond to the transverse eigenvectors. Therefore, the synchronous solution of dynamical network (1) is asymptotically stable if the following system is stable:

()

where 2 ≤ i ≤ N.

To deduce the sufficient condition for stability of system (13), the following assumption is one of the basic prerequisites.

Assumption 5. Suppose that there exists a positive constant ℒ > 0 satisfying ∥Df(·)∥ ≤ ℒ.

This hypothesis is achievable for a large class of systems depicted by , including linear systems, piecewise linear systems, and numerous chaotic systems (e.g., Chua’s circuit [30], Lorenz family [31–33], etc.).

Theorem 6. Suppose that Assumptions 2 and 5 hold. The synchronous solution of network (1) is asymptotically stable provided that c is larger than c₀, where c₀ = − ℒ/λ₂min _1≤k≤n {μ_k}.

Proof. According to Lemma 3 and the previous discussion, asymptotical stability of synchronous solution of network model (1) can be analyzed by investigating the stability of system (13). Consider a positive semidefinite function as

()

and regard V as a Lyapunov candidate. Then the derivation of V along the trajectories of (13) is

()

Introducing the denotation ζ_i≜Q⁻¹η_i (2 ≤ i ≤ N), one has

and

; thus one obtains

()

In view of λ_i < 0 (2 ≤ i ≤ N) and μ_k > 0 (1 ≤ k ≤ n), the derivation of the Lyapunov candidate would be nonpositive given c > −ℒ/λ₂min _1≤k≤n {μ_k}. The largest invariant set of is Ξ = {ζ_i = 0,2 ≤ i ≤ N}. According to LaSalle’s invariance principle [21], all the trajectories of system (13) will converge to Ξ asymptotically for any initial values. In this set, it is plain to see that η_i = 0 for 2 ≤ i ≤ N. That means system (13) is stable, and accordingly the synchronous solution of dynamical network (1) is asymptotically stable.

From Theorem 6, we conclude that whether can synchronization of a general complex dynamical network (1) be achieved depends on the relationship between the coupling strength c and the constant c₀. The term c₀ = −ℒ/λ₂min _1≤k≤n {μ_k} is associated with individual node dynamics (ℒ), inner coupling (min _1≤k≤n{μ_k}), and topology structure (λ₂) of the whole network.

Remark 7. The smaller the c₀ is, the larger the coupling strength c which leads to network synchronization is. In detail, smaller ℒ of single node dynamics or larger min _1≤k≤n {μ_k} of inner-coupling matrix brings about better synchronizability for particular network topology.

Remark 8. It is worth noticing that although the previous result assumes that c > c₀ = −ℒ/λ₂ min _1≤k≤n {μ_k}, the threshold of c may be much smaller than c₀ in reality. In other words, the synchronization criterion for dynamical network (1) is just a sufficient condition.

Remark 9. Theorem 6 reveals that for any topology structure, synchronization of network (1) can be achieved when the coupling strength c is strong enough, provided that Assumptions 2 and 5 hold. Further, it is seen that the synchronous region of dynamical network (1) belongs to Type I from the angle of Master Stability Function method [28] (see Section 4). Accordingly, the eigenvalue λ₂ of the outer-coupling matrix nearest 0 can be used for judging synchronizability of networks.

Remark 10. Although our analysis is founded on a basic hypothesis that the complex network is bidirectionally coupled (the outer-coupling matrix A is symmetric), similar conclusions can be drawn for the case in which this hypothesis is relaxed to unidirectional network.

4. Numerical Simulations

To verify the effectiveness of our main results, we choose the node dynamics as Lorenz system and the inner-coupling matrix as I in model (1), where I represents identity matrix. Topology structures selected in the network are globally coupled network (GCN), star network (SN), and loop network (LN). Then the outer-coupling matrices are A_GCN, A_SN, and A_LN, respectively, where

()

Lorenz system is a typical benchmark chaotic system, which is a simplified mathematical model first developed by Lorenz in 1963 to describe atmospheric convection. The model is a system of three ordinary differential equations now known as the Lorenz equations [31]:

()

which is chaotic when a = 10, b = 8/3, and c = 28.

It is easy to get that ℒ of Lorenz system is 48 and min _1≤k≤n{μ_k} of the inner-coupling matrix I is 1. For dynamical network (1) coupled with 50 nodes, a direct result is

()

Accordingly, because of c₀ = −ℒ/λ₂min _1≤k≤n{μ_k}, one has

()

Then selecting c(GCN) = 1 > c₀(GCN), c(SN) = 50 > c₀(SN), and c(LN) = 3040 > c₀(LN), we have the following error figure to picture the synchronization errors

(1 ≤ i ≤ 50) in dynamical network (1), in which topology structures are chosen as GCN, SN, and LN. See Figure 1.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Synchronization errors (1 ≤ i ≤ 50) for globally coupled network (GCN) with c = 1, H = I (a); (1 ≤ i ≤ 50) for star network (SN) with c = 50, H = I (b); (1 ≤ i ≤ 50) for loop network (LN) with c = 3040, H = I (c).

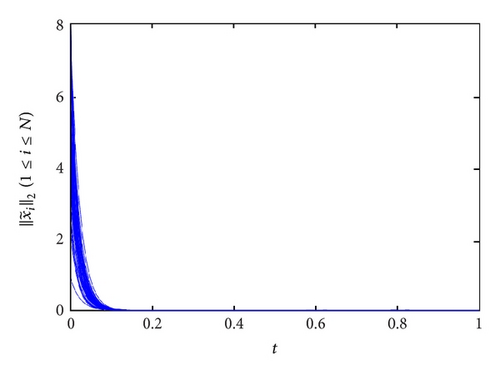
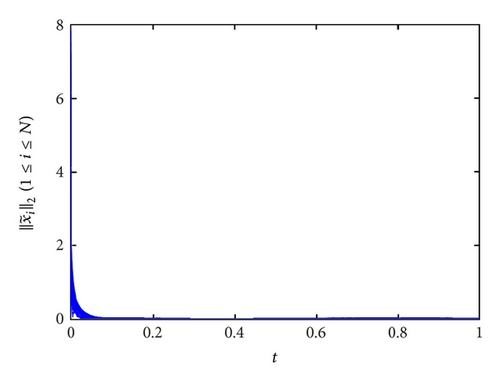
From Figure 1, three networks have all reached synchronization in the condition of c > c₀, which are consistent with Theorem 6.

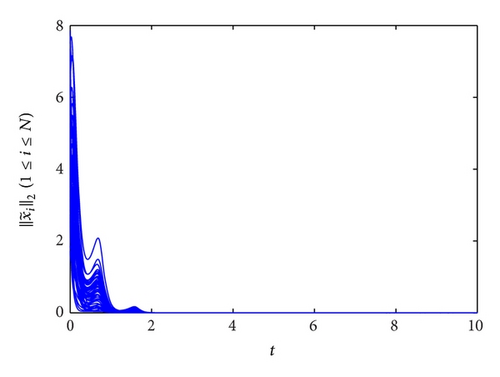
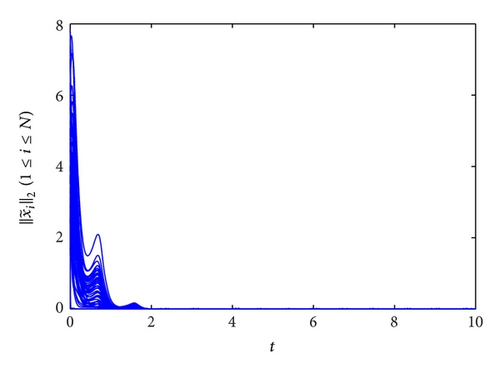
According to Remark 8, the condition c > c₀ for network synchronization is just sufficient. To illustrate, let c be about 10% of the original coupling strength; say, c(GCN) = 0.1, c(SN) = 5, and c(LN) = 310. It is seen from Figure 2 that synchronization of three networks is achieved as well even if the synchronization criterion c > c₀ is not guaranteed.

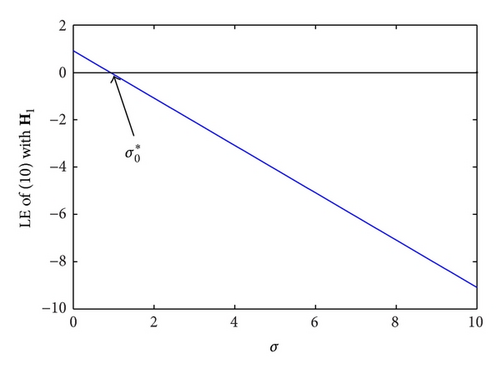
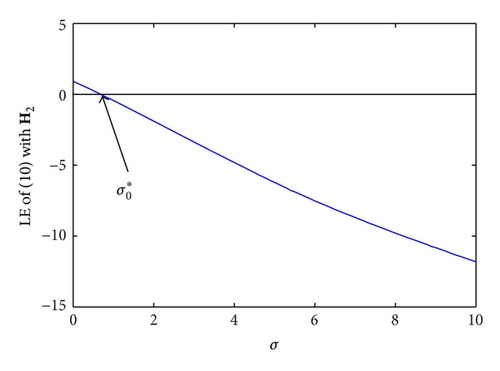
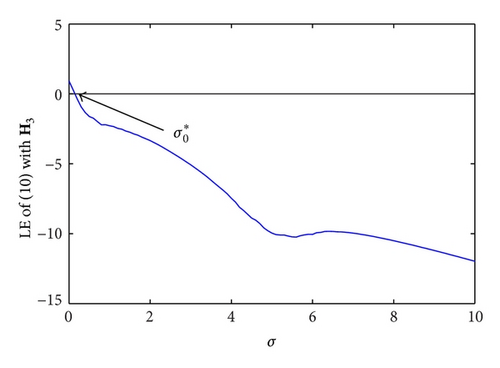
Theorem 6 reveals that if Assumptions 2 and 5 hold, synchronization of network (1) can be achieved provided that c is sufficiently large. In the case of network synchronization, the real number σ = −c λ falls into the synchronous region [28], where λ is any eigenvalue of the outer-coupling matrix A except λ₁ = 0. Furthermore, in view of Theorem 6, the synchronous region of the network is unbounded, which belongs to Type I. If the network belongs to one of the other three types of synchronous region, the coupling strength c which leads to synchronization may be upper bounded or even nonexistent. To clarify the unboundedness of synchronous region for the qualified network, three inner-coupling matrices which satisfy Assumption 2 are employed. We choose Lorenz systems as the nodes in dynamical network (1) and coupled them through H₁, H₂, and H₃. Let H₁ = I, , and . It is easy to verify that the symmetric part of the inner-coupling matrices , , and is positive definite. Figure 3 shows the relationship between Lyapunov Exponents (LEs) of system (13) and σ = −cλ. During the growth of σ, LE of system (13) becomes negative when σ crosses a threshold , and accordingly system (13) is stable. In other words, if synchronization of network (1) is reached, the coupling strength c should be larger than a threshold . Predictably, is much weaker than c₀ got from Theorem 6. Given coupling configuration structure of a dynamical network, the eigenvalues λ_i(1 ≤ i ≤ N) would be certain, and thus network (1) synchronization would ensure . This is in agreement with Remark 9. On the one hand, the exact threshold of coupling strength for network synchronization is smaller than c₀ according to Theorem 6. On the other hand, that is larger than lies in the fact that leads to asynchronization. Although we cannot gain the exact value of so far, our results pave the way for exploring in depth the necessary and sufficient conditions of network synchronization.

5. Conclusions

In conclusion, we have developed a sufficient condition for a general complex dynamical network in the absence of control. We have concluded that if the coupling strength c is larger than c₀ = −ℒ/λ₂min _1≤k≤n{μ_k}, synchronization will be reached in the network, where the symmetric part of the inner-coupling matrix H^s is positive definite. In the sense of Master Stability Function method, we have further illustrated that positive eigenvalues of H^s lead to Type I network with which synchronous region is unbounded. The findings show that the eigenvalue λ₂ of the outer-coupling matrix nearest 0 can be used for exploring synchronizability of a dynamical network with positive definite inner-coupling matrix.

Conflict of Interests

The author declares that there is no conflict of interests regarding the publication of this paper.

Acknowledgment

This work is supported by the National Natural Science Foundation of China under Grants 61004096, 61374173, and 11172215.

References

1 Arenas A., Díaz-Guilera A., and Pérez-Vicente C. J., Synchronization reveals topological scales in complex networks, Physical Review Letters. (2006) 96, 114102, https://doi.org/10.1103/PhysRevLett.96.114102.
10.1103/PhysRevLett.96.114102
CAS PubMed Web of Science® Google Scholar
2 Leyva I., Navas A., Sendina-Nadal I., Almendral J. A., Buldu J. M., Zanin M., Papo D., and Boccaletti S., Explosive transitions to synchronization in networks of phase oscillators, Scientific Reports. (2013) 3, no. article 1281.
10.1038/srep01281
PubMed Web of Science® Google Scholar
3 Szmoski R. M., Pereira R. F., and de Souza Pinto S. E., Effective dynamics for chaos synchronization in networks with time-varying topology, Communications in Nonlinear Science and Numerical Simulation. (2013) 18, no. 6, 1491–1498, https://doi.org/10.1016/j.cnsns.2012.10.005, MR3016901.
10.1016/j.cnsns.2012.10.005
Web of Science® Google Scholar
4 Wu Y., Li C., Wu Y., and Kurths J., Generalized synchronization between two different complex networks, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 1, 349–355, https://doi.org/10.1016/j.cnsns.2011.04.026, MR2826013, ZBL1243.93039.
10.1016/j.cnsns.2011.04.026
Web of Science® Google Scholar
5 Pecora L. M. and Carroll T. L., Synchronization in chaotic systems, Physical Review Letters. (1990) 64, no. 8, 821–824, https://doi.org/10.1103/PhysRevLett.64.821, MR1038263, ZBL0938.37019.
10.1103/PhysRevLett.64.821
CAS PubMed Web of Science® Google Scholar
6 Wu C. W. and Chua L. O., Synchronization in an array of linearly coupled dynamical systems, IEEE Transactions on Circuits and Systems I. (1995) 42, no. 8, 430–447, https://doi.org/10.1109/81.404047, MR1351879, ZBL0867.93042.
10.1109/81.404047
Web of Science® Google Scholar
7 Wang X. F. and Chen G., Synchronization in scale-free dynamical networks: robustness and fragility, IEEE Transactions on Circuits and System I. (2002) 49, no. 1, 54–62, https://doi.org/10.1109/81.974874, MR1874226.
10.1109/81.974874
Web of Science® Google Scholar
8 Motter A. E., Zhou C., and Kurths J., Network synchronization, diffusion, and the paradox of heterogeneity, Physical Review E. (2005) 71, no. 1, 2-s2.0-37649031501, https://doi.org/10.1103/PhysRevE.71.016116, 016116.
10.1103/PhysRevE.71.016116
CAS PubMed Web of Science® Google Scholar
9 Cao J. and Ren F., Exponential stability of discrete-time genetic regulatory networks with delays, IEEE Transactions on Neural Networks. (2008) 19, no. 3, 520–523, 2-s2.0-40949089245, https://doi.org/10.1109/TNN.2007.911748.
10.1109/TNN.2007.911748
PubMed Web of Science® Google Scholar
10 Nishikawa T. and Motter A. E., Maximum performance at minimum cost in network synchronization, Physica D. (2006) 224, no. 1-2, 77–89, https://doi.org/10.1016/j.physd.2006.09.007, MR2301511, ZBL1117.34048.
10.1016/j.physd.2006.09.007
Web of Science® Google Scholar
11 Zhou J., Lu J.-a., and Lü J., Adaptive synchronization of an uncertain complex dynamical network, IEEE Transactions on Automatic Control. (2006) 51, no. 4, 652–656, https://doi.org/10.1109/TAC.2006.872760, MR2228029.
10.1109/TAC.2006.872760
Web of Science® Google Scholar
12 Li Z. and Chen G., Robust adaptive synchronization of uncertain dynamical networks, Physics Letters A. (2004) 324, no. 2-3, 166–178, https://doi.org/10.1016/j.physleta.2004.02.058, MR2067182, ZBL1123.93316.
10.1016/j.physleta.2004.02.058
CAS Web of Science® Google Scholar
13 Zhou J., Lu J.-a., and Lü J., Pinning adaptive synchronization of a general complex dynamical network, Automatica. (2008) 44, no. 4, 996–1003, https://doi.org/10.1016/j.automatica.2007.08.016, MR2530942.
10.1016/j.automatica.2007.08.016
Web of Science® Google Scholar
14 Chen T., Liu X., and Lu W., Pinning complex networks by a single controller, IEEE Transactions on Circuits and Systems I. (2007) 54, no. 6, 1317–1326, https://doi.org/10.1109/TCSI.2007.895383, MR2370589.
10.1109/TCSI.2007.895383
Web of Science® Google Scholar
15 Yu W., Cao J., and Lü J., Global synchronization of linearly hybrid coupled networks with time-varying delay, SIAM Journal on Applied Dynamical Systems. (2008) 7, no. 1, 108–133, https://doi.org/10.1137/070679090, MR2399559, ZBL1161.94011.
10.1137/070679090
Web of Science® Google Scholar
16 Yu W., Chen G., and Lü J., On pinning synchronization of complex dynamical networks, Automatica. (2009) 45, no. 2, 429–435, https://doi.org/10.1016/j.automatica.2008.07.016, MR2527339, ZBL1158.93308.
10.1016/j.automatica.2008.07.016
Web of Science® Google Scholar
17 Yu W., Chen G., Lü J., and Kurths J., Synchronization via pinning control on general complex networks, SIAM Journal on Control and Optimization. (2013) 51, no. 2, 1395–1416, https://doi.org/10.1137/100781699, MR3038018, ZBL1266.93071.
10.1137/100781699
Web of Science® Google Scholar
18 Pecora L. M. and Carroll T. L., Master stability functions for synchronized coupled systems, Physical Review Letters. (1998) 80, no. 10, 2109–2112, 2-s2.0-4243241129.
10.1103/PhysRevLett.80.2109
CAS Web of Science® Google Scholar
19 Barahona M. and Pecora L. M., Synchronization in small-world systems, Physical Review Letters. (2002) 89, no. 5, 4, 054101, https://doi.org/10.1103/PhysRevLett.89.054101, 2-s2.0-3343010976.
10.1103/PhysRevLett.89.054101
CAS PubMed Web of Science® Google Scholar
20 Chen Y., Rangarajan G., and Ding M., General stability analysis of synchronized dynamics in coupled systems, Physical Review E. (2003) 67, no. 2, 4, https://doi.org/10.1103/PhysRevE.67.026209, 2-s2.0-0038396314, 026209.
10.1103/PhysRevE.67.026209
Web of Science® Google Scholar
21 Hassan K. K., Nonlinear Systems, 2002, 3rd edition, Prentice Hall.
Google Scholar
22 Isidori A., Nonlinear Control Systems II, 1st edition, Electronic Industry Press, 2012 (Chinese).
Google Scholar
23 Godsil C. and Royle G., Algebraic Graph Theory, 2001, 207, Springer, New York, NY, USA, https://doi.org/10.1007/978-1-4613-0163-9, MR1829620.
10.1007/978-1-4613-0163-9
Web of Science® Google Scholar
24 Horn R. A. and Johnson C. R., Matrix Analysis, 1985, Cambridge University Press, New York, NY, USA, MR832183.
10.1017/CBO9780511810817
Google Scholar
25 Olfati-Saber R. and Murray R. M., Consensus problems in networks of agents with switching topology and time-delays, IEEE Transactions on Automatic Control. (2004) 49, no. 9, 1520–1533, https://doi.org/10.1109/TAC.2004.834113, MR2086916.
10.1109/TAC.2004.834113
Web of Science® Google Scholar
26 Wu C. W., Synchronization in networks of nonlinear dynamical systems coupled via a directed graph, Nonlinearity. (2005) 18, no. 3, 1057–1064, https://doi.org/10.1088/0951-7715/18/3/007, MR2134084, ZBL1089.37024.
10.1088/0951-7715/18/3/007
PubMed Web of Science® Google Scholar
27 Lu W. and Chen T., New approach to synchronization analysis of linearly coupled ordinary differential systems, Physica D. (2006) 213, no. 2, 214–230, https://doi.org/10.1016/j.physd.2005.11.009, MR2201200, ZBL1105.34031.
10.1016/j.physd.2005.11.009
Web of Science® Google Scholar
28 Chen G. R., Wang X. F., and Li X., Introduction to Complex Networks: Models, Structures and Dynamics, 2012, 1st edition, Higher Education Press.
Google Scholar
29 Lu J. A., Chen J., and Zhou J., On relations between synchronous state and solution of single node in complex networks, Acta Automatica Sinica. In press.
Google Scholar
30 Matsumoto T., Chua L. O., and Komuro M., The double scroll, IEEE Transactions on Circuits and Systems. (1985) 32, no. 8, 797–818, https://doi.org/10.1109/TCS.1985.1085791, MR801479, ZBL0625.58013.
10.1109/TCS.1985.1085791
Web of Science® Google Scholar
31 Lorenz E. N., Deterministic non-periodic flow, Journal of the Atmospheric Sciences. (1963) 20, 130–141.
10.1175/1520-0469(1963)020<0130:DNF>2.0.CO;2
Web of Science® Google Scholar
32 Lü J. and Chen G., A new chaotic attractor coined, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2002) 12, no. 3, 659–661, https://doi.org/10.1142/S0218127402004620, MR1894886, ZBL1063.34510.
10.1142/S0218127402004620
Web of Science® Google Scholar
33 Lü J., Chen G., Cheng D., and Celikovsky S., Bridge the gap between the Lorenz system and the Chen system, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2002) 12, no. 12, 2917–2926, https://doi.org/10.1142/S021812740200631X, MR1956411, ZBL1043.37026.
10.1142/S021812740200631X
Web of Science® Google Scholar

All articles

Criterion for Unbounded Synchronous Region in Complex Networks

Abstract

1. Introduction

2. Preliminaries

3. Main Results

4. Numerical Simulations

5. Conclusions

Conflict of Interests

Acknowledgment

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Criterion for Unbounded Synchronous Region in Complex Networks

Abstract

1. Introduction

2. Preliminaries

3. Main Results

4. Numerical Simulations

5. Conclusions

Conflict of Interests

Acknowledgment

References

Figures

References

Related

Information