Abstract and Applied Analysis
Volume 2013, Issue 1 510903
Research Article
Open Access

Synchronization of Neural Networks with Mixed Time Delays under Information Constraints

Dedong Yang, 

Corresponding Author

Dedong Yang

School of Control Science and Engineering, Hebei University of Technology, Tianjin 300130, China hebut.edu.cn

Search for more papers by this author
He-Xu Sun, 

He-Xu Sun

Hebei University of Science and Technology, Shijiazhuang 050018, China hebust.edu.cn

Search for more papers by this author
Peng Yang, 

Peng Yang

School of Control Science and Engineering, Hebei University of Technology, Tianjin 300130, China hebut.edu.cn

Search for more papers by this author
Tai-Hang Du, 

Tai-Hang Du

School of Control Science and Engineering, Hebei University of Technology, Tianjin 300130, China hebut.edu.cn

Search for more papers by this author
First published: 18 December 2013
https://doi.org/10.1155/2013/510903
Academic Editor: Khalil Ezzinbi

Abstract

This paper investigates the synchronization problem of neural networks with mixed time delays under information constrains. The designed synchronization scheme is built on the framework of hybrid systems. Besides including nonuniform sampling, some other characteristics, such as quantization, transmission-induced delays, and data packet dropouts, are also considered. The sufficient condition that depended on network characteristics is obtained to guarantee the remote asymptotical synchronization of neural networks with mixed time delays. A numerical example is given to illustrate the validity of the proposed method.

1. Introduction

Recently, neural networks have been widely studied by many scholars due to its potential applications in pattern recognition, image processing, signal processing, biology engineering, and information science [1–3]. Moreover, there exists a broad class of neural networks with mixed time delays. Following the development in this field, many master-slave synchronization schemes for neural networks with mixed time delays have been proposed, such as [4–14].

Generally, some useful approaches can be utilized for the synchronization problem of neural networks, which include passivity analysis [5, 12], impulsive control [15, 16], adaptive control [17, 18], and stochastic method [13]. In recent years, the sampled-data control scheme is utilized for the synchronization of neural networks with mixed time delays, such as [10, 11, 14]. However, these schemes did not consider quantization, transmission-induced delays, and data packet dropouts. Essentially, in the range of deterministic systems, the general framework considering information constrains can be divided into three cases: (1) continuous-time models; (2) discrete-time models; (3) hybrid models. In this paper, the networked controller design for asymptotical synchronization of neural networks with mixed time delays is discussed in the framework of hybrid systems. Besides including nonuniform sampling, we also consider other network characteristics, such as quantization, transmission-induced delays, and data packet dropouts. From the view of helpful technologies, the input delay approach and the free-weighting matrix technology are applied to obtain the less conservative condition.

Notation. Throughout this paper, superscripts T and −1 mean the transpose and the inverse of a matrix, respectively, N denotes natural number, Z denotes integer number, Rn denotes the n-dimensional Euclidean space, Rn×m is the set of all n × m real matrices, the identity matrices and zero matrices are denoted by I and 0, respectively, the notation * always denotes the symmetric block in one symmetric matrix, the standard notation >(<) is used to denote the positive (negative)-definite ordering of matrices, and inequality X > Y shows that the matrix X − Y is positive definite.

2. Preliminaries

Consider the following general master-slave neural network with mixed time delays [11]:
()
where , , and xi(t) and yi(t) denote the states of the ith neuron of master and slave neural networks, respectively; , , and g(x(t)) and g(y(t)) denote the neuron activation functions of master and slave neural networks, respectively; C = diag {c1, c2, …, cn} ∈ Rn denotes a diagonal matrix with positive entries; A = (aij) n×n ∈ Rn×n, B = (bij) n×n ∈ Rn×n, and D = (dij) n×n ∈ Rn×n denote the connection weight matrices; u(t) ∈ Rn denotes the control input; denotes the external input vector; d(t) and τ(t) denote the discrete delay and the distributed delay, respectively, and satisfy
()
where μ and τ are constants.

Assumption 1 (see [7].)For i ∈ {1,2, …, n}, the neuron activation functions satisfy

()
where and are some constants, s1, s2 ∈ R, and s1 ≠ s2.

Assumption 2 (see [7].)The neuron activation functions are bounded.

Let the error be e(t) = y(t) − x(t). Then, the synchronization error system can be represented as
()
where f(t): = g(y(t)) − g(x(t)). The networked synchronization controller is designed as
()
where denotes the quantizer, K ∈ Rn×n denotes the controller gain matrix, and are available measurements of y(t) and x(t) at sampling instant , k = 0,1, …, ∞, ik ∈ N denotes the serial number of the available data packet such that {i0, i1, i2, …}⊆{0,1, 2,3, …}, denotes the sampling instant of the available data packet, and denotes the network-induced delay calculated from the instant .

The above controller (5) is related with the quantitative function so the following definition is introduced.

Definition 3 (see [19].)A quantizer is called logarithmic if the set of quantized levels is characterized by

()

The quantizer is assumed to be symmetric; that is, q(−υ) = −q(υ), as described in [19]. Selected as the logarithmic quantizer, q(υ) is given as
()
where i ∈ {1,2, …, n} and σ = (1 − ρ)/(1 + ρ).

Generally, tk denotes the overall sampling instant and all the data packets are assigned as serial numbers. But, the data packets may be discontinuous due to dropouts such that the sampling is nonuniform. Similar to many existing results, the sensor is clock-driven; the controller and actuator are event-driven. The clocks among all the devices are synchronized.

Assumption 4 (see [20].)There exist three constants h > 0, τmin  ≥ 0, and τmax  ≥ 0 such that

()
where h denotes the upper bound of the interval between two consecutive sampling instants and τmin  and τmax  denote the minimum and maximum of network-induced delays, respectively. It is assumed that δmax  denotes the admitted maximum of successive data packet dropouts in network transmissions. Considering condition (8) and successive data packet dropouts, the following result can be obtained:
()

Set ϕ0 : = (1 + δmax )h + τmax  and then the initial condition of e(t) on (t0 − ϕ0, t0] is supplemented as e(t) = ϕ(t), t ∈ (t0 − ϕ0, t0], where ϕ(t) is a continuous function on (t0 − ϕ0, t0]. By the sector bound method as [19], the synchronization error system (4) can be expressed as
()
where , Σ = diag {Σ1, Σ2, …, Σn} and Σi ∈ [−σ, σ]. According to (8) and (9), τmin  ≤ τN(t)<(1 + δmax )h + τmax  and . The control objective is to design the controller gain matrix K such that the synchronization error system (10) is asymptotically stable; that is, e(t) → 0 as t → ∞.

3. Main Result

In this section, the stability of the error system (10) will be analyzed by constructing a corresponding Lyapunov functional. Before beginning the proof procedure, two useful lemmas are introduced.

Lemma 5. Let X be any m × n matrix, for any constant ϵ > 0 and any positive-definite symmetric matrix T, such that

()
for all ζ ∈ Rm, φ ∈ Rn, and T ∈ Rn×n.

Lemma 6 (see [21].)For any constant symmetric matrix G ∈ Rn×n, G = GT > 0, scalar υ > 0, vector function ψ : [t − υ, t] → Rn, such that the integrations in the following are well defined, then

()

Theorem 7. Given scalars τ, μ, and ϕ0 > 0 composed of h, δmax , τmax , and diagonal matrices Σ = diag {Σ1, Σ2, …, Σn}, , and , the synchronization error system (10) is global asymptotically stable in network environments, if there exist matrices , , , , Λ = diag {λ1, λ2, …, λn} ≥ 0, any matrices , with appropriate dimensions, and the controller gain matrix K such that the following condition holds:

()
where
()

Proof. Construct the following Lyapunov functional as

()
where , , , , and ϕ0 = (1 + δmax )h + τmax . Moreover, the following equations hold for any appropriate dimensional matrices N1, N2, N3, M1, M2, and  M3:
()
On the other hand, for any Λ = diag {λ1, λ2, …, λn} ≥ 0, it follows from (3) such that
()
Combining (2), (16), and (17), the corresponding time derivative of  V(e(t)) is given by
()
Using Lemmas 5 and 6 and the inequality
()
the following result can be obtained:
()
where , matrices Θ, M, and N are defined in (13). It is explicit that if
()
then for any nonzero ς(t). Utilizing Schur complement [22], the condition in Theorem 7 can be obtained, and the proof is completed.

Because the uncertain matrix Σ is involved at the condition (13) in Theorem 7, the following theorem is given to obtain a solvable result.

Theorem 8. Given scalars τ, μ, and ϕ0 > 0 composed of h, δmax , τmax , and constant diagonal matrices , , and , the synchronization error system (10) is global asymptotically stable in network environments, if there exist matrices , , , , Λ = diag {λ1, λ2, …, λn} ≥ 0, any matrices , with appropriate dimensions, and the controller gain matrix K such that the following condition holds:

()
where
()

Proof. Utilizing Schur formula and matrix inequality XTY + YTX ≤ XTX + YTY, condition (22) in Theorem 8 is obtained. The proof is completed.

Remark 9. In the above process, the free-weighting matrix technology is applied to complete the proof. Moreover, similar to [23], we can select the new Lyapunov-Krasovskii functional to reduce the conservatism, which utilizes the bounds of the network-induced delay. This will be done in the future works.

4. A Numerical Example

In this section, a numerical example is given to demonstrate the effectiveness of the proposed synchronization scheme.

Example 1. Consider the following master-slave neural network with mixed time delays as in [11, 14]:

()
where
()
d(t) = et/(et + 1), τ(t) = 0.5 sin2 (t), g1(s) = g2(s) = tanh(s), and V(t) = 0. Thus, μ = 0.25 and τ = 0.5. It is assumed that , . According to Assumption 1, the following result is satisfied:
()

The chaotic behaviors of the master and slave systems are given in Figures 1 and 2, with the initial condition chosen as x(0) = [0.2,0.3] T and y(0) = [−0.1,0.6] T, respectively. Setting σ = 0.5, δmax  = 5, τmax  = 0.01 and appropriate matrices Mi  (i = 1,2, 3), the condition (22) in Theorem 8 is feasible for h ≤ 0.001, with the controller gain matrix
()
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Chaotic behavior of the master system.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Chaotic behavior of the slave system with u(t) = 0.

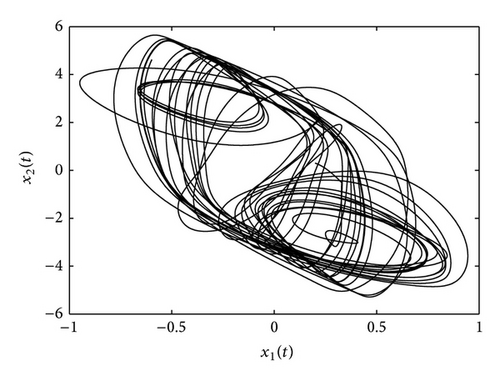
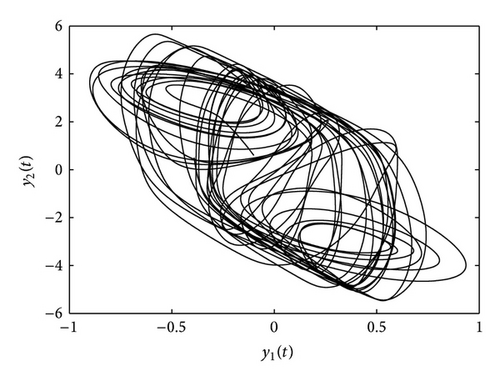
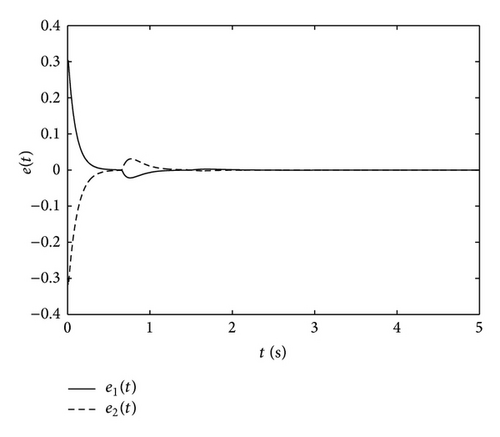
Similar to [14], the initial conditions of the master and slave systems are chosen as x(0) = [0.2,0.3] T and y(0) = [−0.1,0.6] T, respectively. The response curves of the error system are shown in Figure 3 for the upper bound of sampling interval h = 0.001. It shows that the synchronization error converges to zero asymptotically.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
State response curves of the error system.

5. Conclusion

In the present works, the networked synchronization scheme for master-slave neural networks with mixed time delays has been proposed. The error system can be stabilized under information constraints. The obtained result depends on network characteristics. In future works, more performance requirements for synchronization of master-slave neural networks with mixed time delays will be considered in a uniform network topological structure.

Acknowledgments

This work is supported by the Natural Science Foundation of China under Grant 61203076, the Natural Science Foundation of Tianjin City under Grant 13JCQNJC03500, the Natural Science Foundation of Hebei Province under Grant F2012202100, and the Excellent Young Technological Innovation Foundation Project in Hebei University of Technology under Grant 2011005.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.