We are concerned with the estimation of the domain of attraction (DOA) for suboptimal immunity epidemic models. We establish a procedure to determine the maximal Lyapunov function in the form of rational functions. Based on the definition of DOA and the maximal Lyapunov function, a theorem and subsequently a numerical procedure are established to determine the maximal Lyapunov function and the DOA. Determination of the domain of attraction for epidemic models is very important for understanding the dynamic behaviour of the disease transmission as a function of the state of population distribution in different categories of disease states. We focus on suboptimal immunity epidemic models with saturated treatment rate and nonlinear incidence rate. Different from classical models, suboptimal immunity models are more realistic to explain the microparasite infection diseases such as Pertussis and Influenza A. We show that, for certain values of the parameter, larger k value (i.e., the model is more toward the SIR model) leads to a smaller DOA.

1. Introduction

The computing of domain of attraction (DOA), that is, the region where the dynamical system is asymptotically stable, is an interesting research topic in the stability analysis of nonlinear systems such as the systems for compartmental ODE epidemic models. In other words, the mathematical analysis of epidemic models often involves computing the asymptotic stability region for both the disease-free equilibrium and endemic equilibrium. The set of initial states whose corresponding trajectories converge to an asymptotically stable equilibrium point as time increases is known as the stability region or domain of attraction (DOA) of the equilibrium under study. If the initial state lies within the DOA, the disease will evolve towards an endemic state. On the contrary, if the initial state is outside the DOA, the system will converge to a disease-free state. Therefore, it is important to study the DOA of endemic equilibrium.

Lyapunov’s second method (the direct method) is generally used to analyze the stability of epidemic models. In this method, the asymptotic stability of the origin can be examined if a positive definite function whose derivative along the solutions of the system is negative definite. However, it is not only difficult to construct the Lyapunov Function, but also hard to guarantee the asymptotical stability of the equilibrium. Apart from that, it is known even if the Lyapunov function exists in an autonomous ODE, it may not be unique. A maximal Lyapunov function is a special Lyapunov function on S (where S denotes the DOA) which can be used to determine the DOA for a given locally asymptotical stable equilibrium point.

Considerable work on DOA estimation and optimized DOA for epidemic dynamical models has been done. In [1], the authors had computed the DOA in epidemiological models with constant removal rates of infected individuals. An optimization approach for finding the DOA of a class of SEIR models, based on the sum of square optimization, is presented in [2]. Recently, the authors in [3] had adopted a recurrence formula established by Kaslik et al. [4] by using an R-analytical function and the sequence of its Taylor polynomial to construct the Lyapunov function, and solved the linear matrix inequality (LMI) relaxations of a global optimization problem to obtain the DOA. However, all the epidemic models in the papers mentioned above are limited to relatively simple epidemic models, without taking into account nonlinear incidence rates or saturated recovery rates. In this paper, we study the DOA for the suboptimal immunity models with nonlinear incidence rates and saturated recovery rates, by utilizing the maximal Lyapunov function in [5]. Throughout the paper, we focus on DOA for the suboptimal immunity models. This kind of suboptimal immunity models is more appropriate for the study of microparasite infections which usually occurs during childhood. After a primary infection, one may get temporary immunity (namrly, immune protection that will wane over time) or partial immunity (namrly, immunity that is not fully protective). Examples of this kind of diseases include Pertussis (temporary immunity) and Influenza (partial immunity).

The rest of the paper is organized as follows. In Section 2, we will establish a theorem based on [5] and an iterative procedure for the construction of the Maximal Lyapunov Function. In Section 3, we will briefly explain the suboptimal immunity model. In Section 4, two examples of suboptimal immunity models are given to demonstrate the validity of the procedure. A conclusion is then given in Section 5.

2. Maximal Lyapunov Function

Consider the following system

()

where f : ℝⁿ → ℝⁿ is an analytical function with the following properties:

(a)
f(0) = 0, that is, x = 0 is an equilibrium point of system (1);
(b)
all the eigenvalues of the Jacobian matrix at x = 0, that is, (∂f/∂x)(0), have negative real parts, namely, x = 0 is an asymptotically stable equilibrium point.

It is well known that in the Lyapunov sense, if there exists a Lyapunov function for the equilibrium point x = 0 of the system (1), then x = 0 is asymptotically stable.

Definition 1 (Lyapunov function). Let V(x) be a continuously differentiable real-valued function defined on a domain R(0)⊆ℝⁿ containing the equilibrium point x = 0. The function V(x) is a Lyapunov function of the equilibrium x = 0 of the system (1) if the following conditions hold:

(a)
V(x) is positive definite on R(0);
(b)
the time derivative of is negative definite on R(0).

If V(x) is a Lyapunov function which fulfills the conditions in the Definition 1, the estimation of DOA is given by the following definition.

Definition 2. Given an autonomous system (1), where x ∈ ℝⁿ and f(0) = 0, the domain of attraction (DOA) of x = 0 is S_A = {x⁰ ∈ ℝⁿ : lim _t→∞x(t, x⁰) = 0}, where x(·, x⁰) denotes the solution of the autonomous system corresponding to the initial condition x(0) = x⁰.

The Lyapunov function is not unique. A maximal Lyapunov function, V(x), is a special Lyapunov function on S (where S denotes the DOA) which can be used to determine the DOA for a given locally asymptotically stable equilibrium point.

Definition 3 (maximal Lyapunov function [5]). A function V_m(x) : ℝⁿ → ℝ⁺ ∪ {∞} is called a maximal Lyapunov function for the system (1) if

(a)
V_m(0) = 0, V_m(x) > 0, for all x ∈ S, x ≠ 0;
(b)
V_m(x) < ∞ if and only if x ∈ S;
(c)
V_m(x) → ∞ as x → ∂S and/or ∥x∥→∞;
(d)
is well defined and negative definite over S, where S denotes the DOA.

We have the following definition for the DOA of an asymptotically stable equilibrium point which derives from the maximal Lyapunov function.

Definition 4. Suppose we can find a set E⊆ℝⁿ containing the origin in its interior and a continuous function V(x) : E → ℝ⁺ such that

(a)
V(x) is positive definite on E;
(b)
is negative definite on E;
(c)
V(x) → ∞ as x → ∂S and/or as ∥x∥→∞. Then E = S, where S denotes the DOA.

From the above definition, based on the work in [5], we derive the following theorem.

Theorem 5. Consider the nonlinear system of equations , where F_i(·) is a homogeneous function of degree i. Suppose that the linearized system is asymptotically stable at x = 0. Let R_i, Q_i be homogeneous functions of degree i, and the functions R_i and Q_i satisfy the following recursive equations:

()

where Q is a fixed positive definite matrix and k ≥ 3. Then, one has the following Lyapunov functions

()

Proof. Rewrite

()

which satisfy condition (a) in the Definition 3. Differentiating (4) with respect to x, we have

()

One choice to ensure that

is negative definite is

. Then from (5), we have

()

Equating the coefficients of the same degree k of the two sides of (6), we get the following recursive relations:

()

where Q is a fixed positive definite matrix, and k ≥ 3.

Based on Theorem 5, the procedure for obtaining the maximal Lyapunov function and calculating the DOA is established as follows.

Step 1. From the linearized system, F₁ = Ax, find P > 0 such that A^TP + PA = −Q, then set

()

where R₂ = a₁x² + a₂xy + a₃y². In this case, Q is a fixed positive definite matrix. Hence, one of the good choices for Q is the identity matrix.

Step 2. For n = 3, we have

()

where R₃ = a₁x³ + a₂x²y + a₃xy² + a₄y³ and Q₁ = b₁x + b₂y. Equating the coefficients of same degree in (10), we will obtain a system of linear equations in terms of a₁, a₂, a₃, a₄, b₁ and b₂. The solution of these linear equations will be used as constraints in the minimization problem to get e_n(y) in the later steps.

Step 3. For n = 4, we have

()

where R₄ = a₁x⁴ + a₂x³y + a₃x²y² + a₄xy³ + a₄y⁴ and Q₂ = b₁x² + b₂xy + b₃y². Then, we solve the system of linear equations as in Step 2.

Step 4 (optional). For n = 5, we have

()

where R₅ = a₁x⁵ + a₂x⁴y + a₃x³y² + a₄x²y³ + a₅xy⁴ + a₆y⁵ and Q₃ = b₁x³ + b₂x²y + b₃xy² + b₄y³. Then, the system of linear equations is solved. We should address that equations similar to (12) can also be obtained for n > 5.

For each of the Steps 2 and 4, one will lead to a number of choices for the value of the coefficients for R_n and Q_n−2. Consider

()

where e_n(y) is the squared 2-norm of the coefficients of the terms with degree greater than or equal to n + 1 in the expression of

. This ensures that

is negative definite over a neighbourhood of the origin. To make it as similar as possible to

, we take e_n(y) as small as possible. Hence, it creates a new condition that can be formulated as a minimization problem where the constraints are obtained from the recursive relations in each of the steps above.

Step 5. Once we get e_n(y) sufficiently small, say at Step 3, we can have the maximal Lyapunov function as

()

To obtain the DOA, one needs to find the largest possible value C^* when V₄(x) = C^* such that the interior of the resulting ellipsoid is entirely bounded within the region given by

. In this case, one can determine C^* by solving an optimization problem:

()

Then, the set S_A = {x : V₄(x) < C^*} is contained in the DOA S. Appropriate C^* also can be determined manually as suggested in [6]. In this case, one can choose the largest positive value C^* such that the sublevel set S_A = {x : V₄(x) < C^*} is contained in the region given by

. Hence, we obtain the DOA in the form of S_A.

3. Suboptimal Immunity Epidemic Models

In this paper, we estimate the domain of attraction (DOA) for suboptimal immunity epidemic models with saturated treatment/recovery rate and nonlinear incidence rate. Apart from using the saturated treatment/recovery rate, an additional parameter σ is used to form the suboptimal immunity model as in [7]. The new model lies in between the SIS and SIR models.

The suboptimal immunity model with nonlinear incidence rate and saturated treatment/recovery rate is as follows:

()

where all the parameters are positive. We assume that the population is fixed, namely, A/μ = S(t) + I(t) + R(t) and where S denotes susceptible population, I represents infective population, and R is the recovered population. A is the recruitment rate of susceptible population, β is the disease transmission rate, μ is the natural death rate, and T(I) is the recovery rate. We take T(I) = vI + cI/(1 + aI) as the recovery rate function in which c/(1 + aI) and v are, respectively, the recovery rate of the infected population with and with no treatment. The function g(I, S) denotes the incidence rate. In comparison with previous models, our model presented here has various new features and contributions. Firstly, it is more general and includes some previous models as special cases. For example, if we take g(I, S) as βSI², we will have the nonlinear incidence rate. If we take g(I, S) as a bilinear function, then it reduces to the suboptimal immunity model [7], while it reduces to the nonlinear SIR model if T(I) is taken to be zero. It should also be addressed that σ = 1 corresponds to the SIS model in which immunity is assumed not to protect against reinfection, while σ = 0 corresponds to the SIR model in which immunity is assumed to be fully protective and prevents any reinfection. The suboptimal immunity model where σ ∈ [0,1] is more appropriate for the study of microparasite infections which usually occur during childhood. After a primary infection, one may get temporary immunity (namely, immune protection that wanes over time) or partial immunity (namely, immunity that is not fully protective). Examples of this kind of diseases include Pertussis (temporary immunity) and Influenza A (partial immunity) [8]. Secondly, due to the combination of the nonlinearities in both incidence rate and recovery rate, it is hard to obtain exact solution. Hence, estimating its domain of attraction using the numerical procedure is important in order to know whether the disease in a particular state will evolve towards an endemic state or converge to a disease free state.

4. Numerical Examples

Example 1. We consider the following reduced system for the suboptimal immunity model with bilinear incidence rate and saturated treatment rate:

()

where (A, β, v, c, a, μ, k) = (19.2,0.5,1, 10,0.5,1, 0.25) and k = 1 − σ. Rewrite X and Y for I and R, and translate the equilibrium point to the origin by using x = X + 4.549349206 and y = Y + 4.424023809. By using the numerical procedure in Section 2, we have the following result:

()

and C^* = 0.284. Thus, S_A = {x : V₄(x) < 0.284} is an estimate of S for the system (17) when (A, β, v, c, a, μ, k) = (19.2,0.5,1, 10,0.5,1, 0.25). This estimate and its phase portrait are given in Figure 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The DOA when (A, β, v, c, a, μ, k) = (19.2,0.5,1, 10,0.5,1, 0.25) for the model (17).

Consider smaller k, which means the model is more toward the SIS model. Let (A, β, v, c, a, μ, k) = (19.2,0.5,1, 10,0.5,1, 0.15). Rewrite X and Y for I and R, and translate the equilibrium point to the origin by using x = X + 7.494893880 and y = Y + 3.492315487. By using the numerical procedure as given in Section 2, we have the following result:

()

and C^* = 0.4. Thus, S_A = {x : V₄(x) < 0.4} is an estimate of S for the system (17) when (A, β, v, c, a, μ, k) = (19.2,0.5,1, 10,0.5,1, 0.15). This estimate and its phase portrait are given in Figure 2.

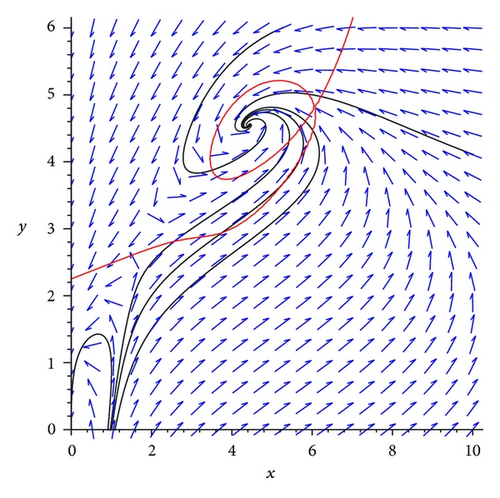
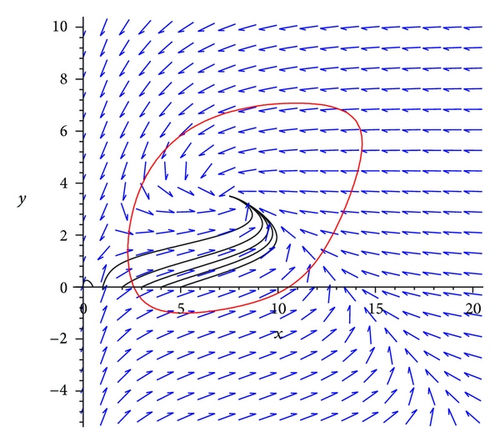
Example 2. We consider the following reduced system for the suboptimal immunity model with nonlinear incidence rate and saturated treatment rate:

()

For this example, we consider the nonlinear incidence rate βSI². According to [9], one of the reasons to consider the nonlinear incidence rate, βS^pI^q, is to represent heterogeneous mixing. Take (A, β, v, c, a, μ, k) = (6,0.5,1.27,2, 4,1, 0.5). Rewrite X and Y for I and R, and translate the equilibrium point to the origin by using x = X + 2.046474176 and y = Y + 1.522295468. By using the numerical procedure in Section 2, we have the following result:

()

and C^* = 0.0002. Thus, S_A = {x : V₅(x) < 0.0002} is an estimate of S for the system (20) when (A, β, v, c, a, μ, k) = (6,0.5,1.27,2, 4,1, 0.5). This estimate and its phase portrait are given in Figure 3.

Here, we study the effect of the value a on the DOA. With the value of a which is ten fold of previous calculation, let (A, β, v, c, a, μ, k) = (6,0.5,1.27,2, 40,1, 0.5). Rewrite X and Y for I and R, and translate the equilibrium point to the origin by using x = X + 2.561174171 and y = Y + 1.651103929. By using the numerical procedure as in Section 2, we have the following result:

()

and C^* = 0.043. Thus, S_A = {x : V₄(x) < 0.043} is an estimate of the DOA for the system (20) when (A, β, v, c, a, μ, k) = (6,0.5,1.27,2, 40,1, 0.5). This estimate and its phase portrait are given in Figure 4.

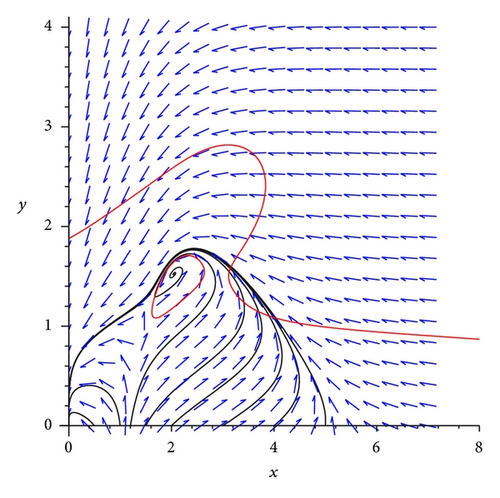
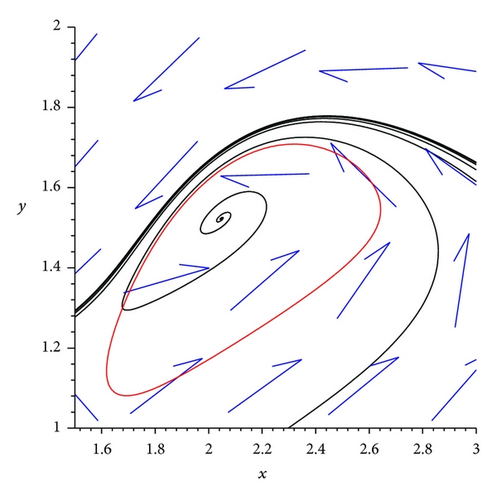
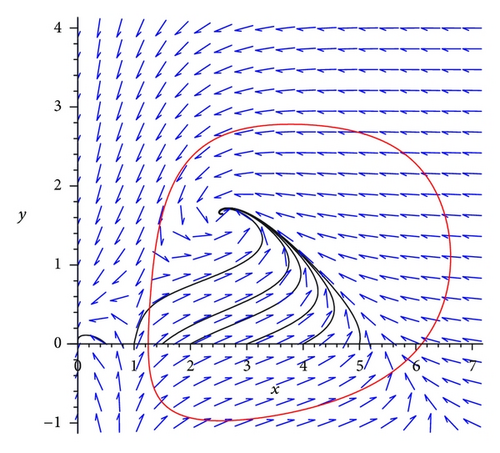
By applying the same procedure, we calculate the DOA when a = 12, and we obtain the DOA as in Figure 5. It is clear that with (A, β, v, c, a, μ, k) = (6,0.5,1.27,2, 12,1, 0.5), increasing the value of a will increase the DOA for the suboptimal model given by (20).

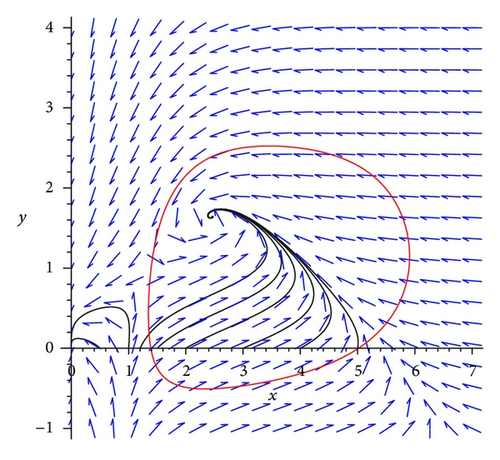
5. Concluding Remarks

In this paper, we deal with the problem of estimating the domain of attraction (DOA) for the suboptimal epidemic model. We have successfully established a procedure to determine the maximal Lyapunov function in the form of rational functions and compute the domain of attraction for epidemic models. Determination of the DOA is extremely important in order to understand the dynamic behaviour of the transmission of disease as a function of the initial population distribution. In our first example, we show that, for certain values of the parameter, a larger k value (i.e., the model is more toward the SIR model) leads to a smaller DOA. In our second example, we show that within certain values of the parameter, decreasing the a value will yield a smaller DOA.

Acknowledgments

The authors are grateful to the anonymous reviewers for their helpful suggestions and comments. The third author wishes to acknowledge the support of the Faculty of Science, Mahidol University.

References

1 Matallana L. G., Blanco A. M., and Alberto Bandoni J., Estimation of domains of attraction in epidemiological models with constant removal rates of infected individuals, Journal of Physics: Conference Series. (2007) 90, no. 1, 2-s2.0-36949030904, https://doi.org/10.1088/1742-6596/90/1/012052, 012052.
10.1088/1742-6596/90/1/012052
Google Scholar
2 Chen X. Y., Li C. J., Lü J. F., and Jing Y. W., The domain of attraction for a SEIR epidemic model based on sum of square optimization, Bulletin of the Korean Mathematical Society. (2012) 49, no. 3, 517–528, https://doi.org/10.4134/BKMS.2012.49.3.517, ZBL1247.34082.
10.4134/BKMS.2012.49.3.517
Web of Science® Google Scholar
3 Zhang Z., Wu J., Suo Y., and Song X., The domain of attraction for the endemic equilibrium of an SIRS epidemic model, Mathematics and Computers in Simulation. (2011) 81, no. 9, 1697–1706, 2-s2.0-79955550073, https://doi.org/10.1016/j.matcom.2010.08.012, ZBL1217.92076.
10.1016/j.matcom.2010.08.012
Web of Science® Google Scholar
4 Kaslik E., Balint A. M., and Balint S., Methods for determination and approximation of the domain of attraction, Nonlinear Analysis, Theory, Methods and Applications. (2005) 60, no. 4, 703–717, 2-s2.0-10644221062, https://doi.org/10.1016/j.na.2004.09.046, ZBL1066.34053.
10.1016/j.na.2004.09.046
Web of Science® Google Scholar
5 Vannelli A. and Vidyasagar M., Maximal lyapunov functions and domains of attraction for autonomous nonlinear systems, Automatica. (1985) 21, no. 1, 69–80, 2-s2.0-0021817154, https://doi.org/10.1016/0005-1098(85)90099-8, ZBL0559.34052.
10.1016/0005-1098(85)90099-8
Web of Science® Google Scholar
6 Rozgonyi S., Hangos K. M., and Szederkényi G., Determining the domain of attraction of hybrid non-linear systems using maximal lyapunov functions, Kybernetika. (2010) 46, no. 1, 19–37, 2-s2.0-77953582632, ZBL1194.34018.
Web of Science® Google Scholar
7 Pang J., Cui J. A., and Hui J., Rich dynamics of epidemic model with sub-optimal immunity and nonlinear recovery rate, Mathematical and Computer Modelling. (2011) 54, no. 1-2, 440–448, 2-s2.0-79955476524, https://doi.org/10.1016/j.mcm.2011.02.033, ZBL1225.37108.
10.1016/j.mcm.2011.02.033
Google Scholar
8 Gomes M. G. M., White L. J., and Medley G. F., Infection, reinfection, and vaccination under suboptimal immune protection: epidemiological perspectives, Journal of Theoretical Biology. (2004) 228, no. 4, 539–549, 2-s2.0-1642350077, https://doi.org/10.1016/j.jtbi.2004.02.015.
10.1016/j.jtbi.2004.02.015
PubMed Web of Science® Google Scholar
9 Liu W. M., Levin S. A., and Iwasa Y., Influence of nonlinear incidence rates upon the behavior of SIRS epidemiological models, Journal of Mathematical Biology. (1986) 23, no. 2, 187–204, 2-s2.0-0022298258.
10.1007/BF00276956
CAS PubMed Web of Science® Google Scholar

Citing Literature

All articles

Computation of the Domain of Attraction for Suboptimal Immunity Epidemic Models Using the Maximal Lyapunov Function Method

Abstract

1. Introduction

2. Maximal Lyapunov Function

3. Suboptimal Immunity Epidemic Models

4. Numerical Examples

5. Concluding Remarks

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Computation of the Domain of Attraction for Suboptimal Immunity Epidemic Models Using the Maximal Lyapunov Function Method

Abstract

1. Introduction

2. Maximal Lyapunov Function

3. Suboptimal Immunity Epidemic Models

4. Numerical Examples

5. Concluding Remarks

Acknowledgments

References

Citing Literature

Figures

References

Related

Information