An optimal H_∞ tracking-based indirect adaptive fuzzy controller for a class of perturbed uncertain affine nonlinear systems without reaching phase is being developed in this paper. First a practical Interval Type-2 (IT2) fuzzy system is used in an adaptive scheme to approximate the system using a nonlinear model and to determine the optimal value of the H_∞ gain control. Secondly, to eliminate the trade-off between H_∞ tracking performance and high gain at the control input, a modified output tracking error has been used. The stability is ensured through Lyapunov synthesis and the effectiveness of the proposed method is proved and the simulation is also given to illustrate the superiority of the proposed approach.

1. Introduction

After the approximation-based adaptive fuzzy controller (AFC) of Wang [1] for a class of uncertain affine nonlinear system, many approaches and ideas have been developed in recent years to overcome the difficulty in controller design [2–4].

The primary feature that characterizes the fuzzy logic is its high capacity for representing and modelling the nonlinear systems with imprecise uncertainty, as the universal approximation theorem, by Lee and Tomizuka, illustrates [5].

Many effective adaptive fuzzy control schemes have been developed to incorporate with human expert knowledge and information in a systematic way, which can also guarantee various stability and performance [6]. The most important issue for Fuzzy Logic Systems (FLSs) is how to get a system design with the guarantee of stability and control performance [7–9].

An adaptive fuzzy control system includes uncertainties caused by unmodeled dynamics, Fuzzy Approximation Errors (FAEs), and external disturbance, which cannot be effectively handled by the FLS and may degrade the tracking performance of the closed-loop system [10, 11]. The AFC combined with H_∞ control technique is an effective approach for rejecting those uncertainties, ensuring stability and consistent performance [12–14].

The research of fuzzy model under H_∞ has attracted many attentions in recent years [4, 15], such as the apparent similarities between H_∞ and fuzzy control which motivate considerable research efforts in combining the two approaches for achieving more superior performance.

Moreover, to the best of our knowledge, the control gain needs to be known in all previous H_∞, indirect adaptive fuzzy controller (HIAFC) approaches, such as the arbitrary choice of the gain which does not always give good results, for which we propose in this work a method for extracting automatically the optimum gain from the Lyapunov equation whilst respecting system stability.

The convergence of the system in the initial time needs the appearance of high gain at the control input, and the high gain is unavoidable in all previous H_∞ tracking-based AFC approaches. The best method to solve the problem of the tradeoffs between H_∞ tracking performance and high gain at the control input is to eliminate the reaching phase. During the reaching phase the tracking error cannot be controlled directly and the system response is sensitive to parameter uncertainties. Several methods have been proposed to completely eliminate the reaching phase [16].

This paper focuses on a class of Single-Input Single-Output (SISO) perturbed uncertain affine nonlinear systems involving external disturbances without exact knowledge of dynamic functions. Firstly, we use the type-2 fuzzy technique to determine the optimal value of the H_∞ gain control. Secondly, a modified output tracking error is used to eliminate the reaching phase [4].

The paper is organized as follows: Section 2 presents the problem statement. Section 3 gives the control design strategy. An illustration example is described in Section 4. Finally, the simulation results are being used to demonstrate the effectiveness and performance of the proposed approach.

2. Problem Formulations

Considering the following nth-order SISO affine nonlinear dynamical system, Chen et al. [14]:

()

Or equivalently

()

where

is the state vector of the systems which is assumed to be available for measurement, u ∈ R and y ∈ R are, respectively, the input and the output of the systems.

and

are two functions that are unknown, nonlinear, and continuous; d(t) denotes the external disturbance. For (1) to be controllable, we require that

for

in certain controllability region. Assume that the given reference

is bounded and have up to (n − 1) bounded derivatives. The reference vector is denoted as

. Define the tracking error e = y_r − y and the error vector

Assumption 1. For all , there exist unknown bounded , and such that , and hold, where compact set D ⊂ Rⁿ is a certain controllable region.

During the AFC design, to improve the tracking performance under the external disturbance, an additional H_∞ compensator associated with an attenuation level is usually suggested to apply, Chen et al. [14]. If the prescribed attenuation level is smaller, the tracking performance is better while the control input gain is higher as the output of the H_∞ compensator becomes larger.

To avoid high control input gain, we have modified the following output tracking error Yilmaz and Hurmuzlu [16]:

()

where (condition 1) ψ(t) is designed to make E(t) small enough at the onset of the motion t = 0, and (condition 2) should rapidly vanish as the motion evolves at t > 0.

A suggested ψ(t) is given in the following exponential form:

()

with γ⁽ⁱ⁾(t₀) (i = 0,1, …, n − 1) is selected to satisfy condition one and F(t) is selected to satisfy condition two. For the selections of γ(t) ⁽ⁱ⁾(t₀) one can follow the methods in Yilmaz and Hurmuzlu [16], on the other side α is selected to satisfy condition two [4].

Now, the objective of this paper is to determine the optimal value of the H_∞ gain control, in a way to force y(t) to follow a given bounded reference signal y_r(t).

Let us denote the parameter tracking error for some parameter estimate and optimal parameter estimate of Type-2 Fuzzy Logic System (T2FLS). Let w denote the sum of error due to fuzzy modelling approximations. Then our design objective is to impose an adaptive fuzzy control algorithm so that the following asymptotically stable tracking

()

is achieved while w = 0 (i.e., in the case of perfect fuzzy approximation and free of external disturbance). While w appears, the following H^∞ tracking performance is requested [17]:

()

where

. V is the Lyapunov function, Q = Q^T > 0, ρ ∈ R⁺ is the prescribed attenuation level, and w ∈ L₂[0, T].

Q, V, and w will be defined in the next subsection.

Remark 2. (i) The roots of polynomial in the characteristic equation of (6) are all in the open left-half plane via an adequate choice of coefficients k₀, k₁, …, k_n−1.

(ii) If the system starts with initial condition V(0) = 0, then the H^∞ performance in (7) can be rewritten as

()

where

, and

, that is, the L₂-gain form w to the tracking error

must be equal to or less than ρ.

3. Control Design Strategy

3.1. Indirect Adaptive Control Scheme

In this section, we propose a new optimal H_∞ tracking-based indirect adaptive output-feedback fuzzy controller that eliminates the reaching phase, with guaranteed stability of the closed loop system. Based on the combination of the H_∞ optimal control with fuzzy logic control, using fuzzy identifier and fuzzy logic control, the H_∞ control design relies on the solution of an algebraic Riccati equation.

If the system (1) is well known and

then the control should be designed to have the following idealized control law:

()

where

However, in practice the functions

and

are unknown, thus the ideal controller in (9) cannot be realized, and the choice of the H^∞ gain control ℜ does not always give good results. In this case the nonlinear functions

and

are approximated using T2-fuzzy systems universal approximation property and by the same technique we determine the optimal H^∞ gain control. Hence, the fuzzy adaptive control law is as follows:

()

where

defined the auxiliary control employed to attenuate the approximation error of the fuzzy model and to eliminate the external disturbance.

, , and are the type-2 fuzzy approximation of ,, and ℜ.

3.2. Interval Type-2 Fuzzy Logic System (IT2FLS)

For an Interval Type-2 Fuzzy Logic System IT2FLS with M, total number of IF-THEN rules in the rule base, the jth rule can be written as follows:

()

Equation (11) represents a T2 fuzzy relation between the input and the output spaces of the FLS, where

’s are antecedent type-2 sets, y is the output, and θ_j’s are the consequent T2 fuzzy singleton.

Since fuzzy sets are type-2, we need to perform the reduction operation type. This operation will give each function estimated

two vector of the fuzzy basis functions [18]

()

is the interval set determined by two end points

and

, and

is the firing interval.

Accordingly, the firing interval bounds for the ith rule of an IT2FLS with n inputs,

and

, can be rewritten as follows:

()

Using the centre of gravity, the defuzzified crisp output for each output is given by Liang and Mendel [19]:

()

can be represented as a vector of fuzzy basis functions (FBFs) expansion as follows:

()

is the FBF vector of

such that

whose components are given by

()

represents the conclusion of T2FLS.

Similar to the foregoing we have

()

Substituting (17) and (15) in (14) then the output of the T2FLS can be given as follows:

()

where

The previous equation (18) will be used, in an indirect adaptive control, to approximate the unknown system dynamics and to determine the optimal H_∞ gain control.

Therefore the expression (18) can be expressed as:

()

Define the compact sets

()

where M_f, M_g, and M_ℜ are given constants.

The minimum approximation error is defined by

()

where

, and

are an optimal parameter vector defined as

()

where r is a positive constant used below.

3.3. H_∞ Tracking Performance Design in Indirect Adaptive Fuzzy System

Choose the H_∞ compensator u_h as

()

where P is the solution of the following Riccati equation:

()

where Q > 0, ρ is prescribed attenuation level and r is positive constant verified r < 2ρ².

Theorem 3. If we select the following adaptive fuzzy control law in the nonlinear system (1)

()

where

()

With P = P^T ≥ 0 is the solution of the Riccati equation (25), then the H^∞ tracking performance in (7) is achieved for a prescribed attenuation level ρ.

Proof. We have

()

And the equation of the control already proposed

()

where

()

And

Utilising (3) and substituting (30) into (31), the output error dynamics may be expressed as

()

The error dynamics can be represented by

()

where

()

Consider the following Lyapunov function:

()

where

()

Utilizing (25) and (32) into (38)

()

where w is defined in (21), the

can be written as

()

By consideration of the update law (27), (28), (23), and (29),

can be written as

()

Integrating the above equality from t = 0 to T yields (0 ≤ T ≤ ∞):

()

Since V(T) ≥ 0 the above inequality implies the following inequality:

()

Hence, the inequality (7) holds. This completes the proof of theorem. So the system is stable and the error will asymptotically converge to zero; that is, H_∞ a performance is achieved.

4. An Illustrative Example

4.1. The Dynamic Model

In this section consider a single-link robot manipulator governed by the following dynamic model [20]:

()

where x₁: Position, x₂: Velocity,

: Nonlinear term depending on

, m, d_f: Mass and damping, l: Length of the manipulator, g_v: is the gravitational acceleration and d(t) = 0.1*rand n is the disturbance.

We assume that the position x₁ and the velocity x₂ are available for measurements, where m = 2 kg, l = 1 m, g_v = 9.8 m/s², and d_f = 1.0 kg m²/s.

4.2. Controller Parameters Design

Step 1. In the first step, we need to define the type-2 fuzzy sets for modelling the unknown functions entering into the creation of the control law and to determine the optimal value of the H_∞ gain control. The choice of the number of fuzzy sets and constant M_f, M_g, and M_ℜ are related to knowledge of expert on the system.

The fuzzy membership functions are chosen as

()

such as cp₁ = −cn₁ = π/3, cp₂ = −cn₂ = π, sig₁ = 5, and sig₂ = 1.53 with M_f = 6, M_g = 1, and M_ℜ = 10.

Step 2. Determine parameters of the modified error E in (3).

Choose α = 5 in (5).

To determine γ(t) in (4) one can follow the method in Yilmaz and Hurmuzlu, and one can make

()

with

()

Thus, one gets

()

Step 3. Design parameters of the control law.

The control parameters for simulation are chosen as follows: k₀ = 1, k₁ = 2, γ₁ = 0.002, γ₂ = 0.0001, γ₃ = 0.001, Q = 5 eye (2), and ρ = 0.1.

The solution to Riccati equation for Q is

()

4.3. Simulation Result

Simulation result is presented to validate performance and robustness of the proposed approaching that we have been using T-S fuzzy logic to determine automatically the gain of the H_∞ control and modifying the output tracking error to eliminate the reaching phase.

Three fuzzy sets for each input have been found sufficient for an efficient system design. Fuzzy sets for inputs x₁ and x₂ are defined according to the membership functions presented forward in Step 1.

The sampling time is defined as 10 ms and the running time as 15 s.

Figure 1 present a responses of the output y(t) versus the desired output y_r(t).

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Reponses of the y(t) and the y_r(t).

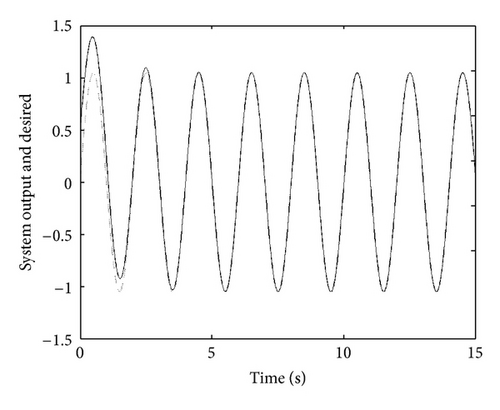
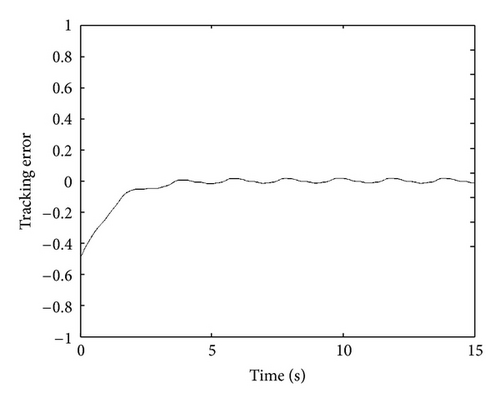
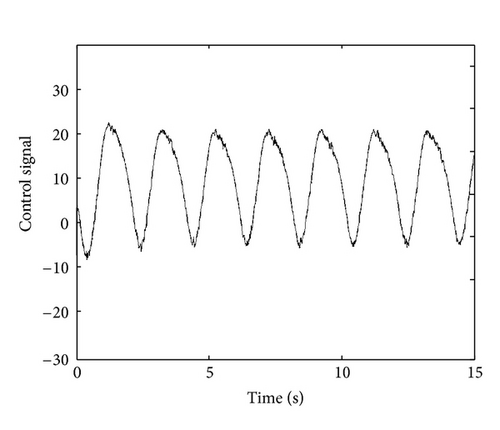
Figures 2 and 3 present successively the tracking error and the control signal that we apply the proposed method.

5. Conclusions

In this paper, we have proposed a new method to determine the optimal value of the H_∞ gain control based on type-2 fuzzy logic systems, and to eliminate the trade-off between H_∞ tracking performance and high gain at the control input, we have used the modification in the output tracking error.

The parameters of the dynamics systems are estimated by using the fuzzy model. Furthermore, the parameters can be tuned on-line by the adaptive law based on Lyapunov synthesis.

References

1 Wang L. X., Stable adaptive fuzzy control of nonlinear systems, IEEE Transactions on Fuzzy Systems. (1993) 1, no. 2, 146–155.
Google Scholar
2 Farrell J. A. and Polycarpou M. M., Adaptive Approximation based Control: Unifying Neural, Fuzzy and Traditional Adaptive Approximation Approaches, 2006, John Wiley & Sons, Hoboken, NJ, USA.
10.1002/0471781819
Google Scholar
3 Haisen K. and Jiang L., Adaptive control for a class of nonlinear system with redistributed models, Journal of Control Science and Engineering. (2012) 2012, 6, 409139, https://doi.org/10.1155/2012/409139.
10.1155/2012/409139
Google Scholar
4 Pan Y., Joo Er M., Huang D., and Wang Q., Fire-rule-based direct adaptive type-2 fuzzy H_∞ tracking control, Engineering Applications of Artificial Intelligence. (2011) 24, 1174–1185.
Google Scholar
5 Lee H. and Tomizuka M., Robust adaptive control using a universal approximator for SISO nonlinear systems, IEEE Transactions on Fuzzy Systems. (2000) 8, no. 1, 95–106, 2-s2.0-0033876064.
Google Scholar
6 Bernal M. and Guerra T. M., Generalized non-quadratic stability of continuous-time Takagi–Sugeno models, IEEE Transactions on Fuzzy Systems. (2010) 18, 815–822.
Google Scholar
7 Zhang Y., Liu C., and Mu X., Hybrid feedback stabilization of fuzzy nonlinear systems, Journal of Control Science and Engineering. (2011) 2011, 7, 2-s2.0-79953285616, https://doi.org/10.1155/2011/579871, 579871.
10.1155/2011/579871
Google Scholar
8 Nguang S. K. and Assawinchaichote W., H_∞ filtering for fuzzy dynamical systems with D stability constraints, IEEE Transactions on Circuits and Systems I. (2003) 50, no. 11, 1503–1508, 2-s2.0-0242527254, https://doi.org/10.1109/TCSI.2003.818624.
Google Scholar
9 Golea N., Golea A., and Benmahammed K., Stable indirect fuzzy adaptive control, Fuzzy Sets and Systems. (2003) 137, no. 3, 353–366, 2-s2.0-0042878505, https://doi.org/10.1016/S0165-0114(02)00279-8.
Google Scholar
10 Tong S., Tang J., and Wang T., Fuzzy adaptive control of multivariable nonlinear systems, Fuzzy Sets and Systems. (2000) 111, no. 2, 153–167.
Google Scholar
11 Tong S., Chen B., and Wang Y., Fuzzy adaptive output feedback control for MIMO nonlinear systems, Fuzzy Sets and Systems. (2005) 156, 285–299.
Google Scholar
12 Rigatos G. G., Adaptive fuzzy control with output feedback for H^∞ tracking of SISO nonlinear systems, International Journal of Neural Systems. (2008) 18, no. 4, 305–320, 2-s2.0-51449095218, https://doi.org/10.1142/S0129065708001610.
Google Scholar
13 Yoneyama J., Nishikawa M., Katayama H., and Ichikawa A., Design of output feedback controllers for Takagi-Sugeno fuzzy systems, Fuzzy Sets and Systems. (2001) 121, no. 1, 127–148, 2-s2.0-0035400789, https://doi.org/10.1016/S0165-0114(99)00141-4.
Google Scholar
14 Chen B. S., Lee C. H., and Chang Y. C., H_∞ tracking design of uncertain nonlinear SISO systems: adaptive fuzzy approach, IEEE Transactions on Fuzzy Systems. (1996) 4, no. 1, 32–43, 2-s2.0-0030083069.
Google Scholar
15 Pan Y., Zhou Y., Sun T., and Joo Er M., Composite adaptive fuzzy H_∞ tracking control of uncertain nonlinear systems, Neurocomputing. (2013) 99, 15–24.
Google Scholar
16 Yilmaz C. and Hurmuzlu Y., Eliminating the reaching phase from variable structure control, Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME. (2000) 122, no. 4, 753–757, 2-s2.0-0000641680.
Google Scholar
17 Doyle J. C., Glover K., Khargonekar P. P., and Francis B. A., State space solution to standard H^∞ control problems, IEEE Transactions on Automatic Control. (1989) 34, no. 8, 831–847, 2-s2.0-0024715909, https://doi.org/10.1109/9.29425.
Google Scholar
18 Mendel J. M., Rule-Based Fuzzy Logic Systems’: Introduction and New Directions, 2001, Prentice-Hall, Englewood Cliffs, NJ, USA.
Google Scholar
19 Liang Q. and Mendel J., Interval Type-2 fuzzy logic systems’: theory and design, IEEE Transactions on Fuzzy Systems. (2000) 8, 535–550.
Google Scholar
20 Mei F., Man Z., and Nguyen T., Fuzzy modeling and tracking control of nonlinear systems, Mathematical and Computer Modeling. (2001) 33, no. 6-7, 759–770.
Google Scholar

Citing Literature

All articles

Optimal Robust Adaptive Fuzzy H_∞ Tracking Control without Reaching Phase for Nonlinear System

Abstract

1. Introduction

2. Problem Formulations