We study the subject of a behaviour of the solutions of systems with sequential fractional h-differences. We give formulas for the unique solutions to initial value problems for systems in linear and semilinear cases. Moreover, the sufficient condition that guaranties the positivity of considered systems is presented.

1. Introduction

The first definition of the fractional derivative was introduced by Liouville and Riemann at the end of the 19th century. Later on, in the late 1960s, this idea was used by engineers for modeling various processes. Thus the fractional calculus started to be exploited since that time. This calculus is a field of mathematics that grows out of the traditional definitions of integrals, derivatives, and difference operators and deals with fractional integrals, derivatives, and differences of any order. Many authors prove that fractional differential and difference equations are more adequate for modeling physical and chemical processes than integer-order equations. Fractional differential and difference equations describe many phenomena arising in engineering, physics, economics, and science. In fact, several applications can be found in viscoelasticity, electrochemistry, electromagnetic, and so forth. For example, Machado [1] gave a novel method for the design of fractional order digital controllers. Fractional difference calculus has been investigated by many authors, for example, [2–12] and others. In particular, different delta and nabla type fractional differences have been studied in [13–15], where the authors relate these differences by deriving some dual identities. The calculus of fractional h-differences was given, for instance, in [5, 10, 16–19]. The properties of systems defined by the fractional difference equations where studied, for example, in [20–24]. There exist definitions of sequential operators in continuous case with different types of derivatives like Caputo type, Riemann-Liouville type, and Hadamard type, see, for example, [9, 12, 25–27]. In parallel with this paper we developed the theory of fractional h-differences with sequential operators in the paper [28], where the approximation of continuous fractional sequential derivative is considered. We compute different formulas of solutions and then we try to check the system′s behaviour, precisely the positivity of solutions. As far as we know the subject of positivity is well developed for fractional linear systems with continuous time; see [8, 29–32]. However, positivity of fractional discrete systems with sequential h-differences is still a field to be examined. In the present paper we open our studies in this field. We give formulas for the unique solutions to initial problems for systems in linear and semilinear cases. Moreover, the positivity of systems with sequential h-differences is considered. We consider systems with sequential h-differences of Caputo type, while in [32] systems with Grünwald-Letnikov operator are studied. It is worth to add that in [32] (and references within) the considered systems are not of sequential type. Additionally, we have the exact formulas of the solutions of the systems both with the sequential differences and with the ordinary differences while in [32] the recurrence form of solution for discrete systems with Grünwald-Letnikov difference is given.

The paper is organized as follows. In Section 2 all preliminary definitions, facts, and notations are gathered. Section 3 presents systems with sequential fractional differences with results on uniqueness of solutions. We include semilinear systems in Section 4. The Section 5 concerns positivity of considered systems. Finally, the illustrative example is presented.

2. Preliminaries

Let us denote by ℱ_D the set of all real valued functions defined on D. Let h > 0, α > 0 and put (hℕ) _a : = {a, a + h, a + 2h, …}, where a ∈ ℝ. Let

()

Then the operator σ : (hℕ) _a → (hℕ) _a is defined by σ(t): = t + h. The next two definitions of h-difference operator were originally given in [16, 17].

Definition 1. For a function the forward h-difference operator is defined as

()

while the h-difference sum is given by

()

where t = a + (n + 1)h, n ∈ ℕ₀ and

Definition 2. For arbitrary α ∈ ℝ the h-factorial function is defined by

()

where Γ is the Euler gamma function, that is,

for all z ∈ ℂ such that Rez > 0, (t/h) ∉ ℤ₋ : = {−1, −2, −3, …}, and we use the convention that division at a pole yields zero.

Notice that if we use the general binomial coefficient

, then (4) can be rewritten as

()

In the sequel we need the following technical properties.

Proposition 3 (see [12].)Let α ∈ ℝ.

(1)
For j ∈ ℕ₀ one has , where α, j are such that both sides are well defined;
(2)
For n ∈ ℕ₀ one has ;
(3)
For k ∈ ℕ₁ one has .

The next definition with another notation was stated in [17]. Here we use more suitable summations.

Definition 4. For a function the fractional h-sum of order α > 0 is given by

()

where t = a + (α + n)h, n ∈ ℕ₀. Moreover, we define

It is important to notice that the operator changes the domains of functions.

Remark 5. Note that .

According to the definition of h-factorial function the formula given in Definition 4 can be rewritten as

()

for t = a + (α + n)h, n ∈ ℕ₀. Observe that

and for α = 1 we have again (3).

Remark 6. In [7] one can find the following form of the fractional h-sum of order α > 0:

()

that can be useful in implementation.

The following definition can be found in [33] for h = 1 or in [10] for an arbitrary h > 0.

Definition 7. Let α ∈ (0,1]. The Caputo h-difference operator of order α for a function is defined by

()

Remark 8. Note that , where α ∈ (0,1].

We need the power rule formulas in the sequel. Firstly, we easily notice that for p ≠ 0 the well-defined h-factorial functions have the following property:

()

More properties of h-factorial functions can be found in [10]. In our consideration the crucial role plays the power rule formula presented in [16], that is,

()

where

, r ∈ (hℕ) _a, t ∈ (hℕ) _a+αh. Note that using the general binomial coefficient one can write (11) as

()

If ψ ≡ 1, then we have for μ = 0, a = (1 − α)h and t = nh + a + αh

()

Let us define special functions that we use in the next section to write the formula for solutions.

Definition 9. For α, β > 0 we define

()

where n belongs to the set of integers ℤ, k, s ∈ ℕ₀ and μ = kα + sβ.

Remark 10. It is worthy to notice that for n ∈ ℕ₀

(a)
φ_0,0(nh) = 1;
(b)
and the values are neglected for n = 0;
(c)
φ_k,s((n − l)h) = (Γ(n − l + 1 + kα + sβ))/(Γ(kα + sβ + 1)Γ(n − l + 1)) and as the division by pole gives zero, the formula works also for n < l, l ∈ ℕ₀;
(d)
, l ∈ ℕ₀.

We also need the following proposition.

Proposition 11. Let α, β ∈ (0,1], h > 0 and a = (α − 1)h, b = (β − 1)h. Then for n ∈ ℕ_l+1, l ∈ ℕ₀

()

Proof. We show only equality (15), as (16) is a symmetric one.

Let μ : = kα + sβ. For r ∈ (hℕ) _lh we define the following h-factorial function . Since

()

for n ≥ l and φ_k,s((m − l)h) = 0 for m < l, by (11) we get

()

where t = a − lh + nh. Hence

()

From the application of the power rule follows the rule for composing two fractional h-sums. The proof for the case h = 1 can be found in [7]. For any positive h > 0 the proof is presented in [10].

Proposition 12. Let x be a real valued function defined on (hℕ)_a, where a, h ∈ ℝ, h > 0. For α, β > 0 the following equalities hold:

()

where t ∈ (hℕ)_a+(α+β)h.

The next proposition gives a useful identity of transforming Caputo fractional difference equations into fractional summations for the case when an order is from the interval (0,1].

Proposition 13 (see [10].)Let α ∈ (0,1], h > 0, a = (α − 1)h and let x be a real valued function defined on (hℕ)_a. The following formula holds:

()

The operators presented above can be extended to vectors in a componentwise manner.

3. Solutions of Systems with Sequential Fractional Differences

Let α, β ∈ (0,1] and x : (hℕ)_a → ℝ^N. Moreover, let us take a = (α − 1)h and b = (β − 1)h. Then we define

()

Note that y : (hℕ)_b → ℝ^N. Then we apply the next difference operator of order β on the new function y and consider here an initial value problem stated by the system

()

where f : (hℕ)₀ × ℝ^N → ℝ^N, with initial values

()

where x_a, x₀ are constant vectors from ℝ^N.

Solutions of the state equations (23) and (24) of the sequential fractional discrete-time system can be computed in the recursive way. From Definition 7 and by Proposition 3, (23) can be written as

()

Since by Proposition 3 the following relation

holds, one gets

()

Repeating the same computation for (24) one gets

()

Hence,

()

Then using the Chu-Vandermonde identity, that is,

, α, β ∈ ℝ, k ∈ ℤ, one gets

()

Then by Proposition 3, we have

()

Consequently, since h^αx₀ = x(a + h) − x(a), x(a + 2h) = h^α+β · f(0, x(a)) − αx(a)+(1 + α) · x(a + h) and for n ≥ 1

()

Using Proposition 3 we get for n ≥ 1

()

Therefore the solution of (23) and (24) is given recursively by the following formula:

()

Another possibility of computing the solution of (23) and (24) is to use Proposition 13 twice and then, for n ≥ 1, we get:

()

Hence

()

where

. Nextly,

()

where

Firstly we prove the formula for the unique solution in linear case of (23) and (24): f(nh, x(nh + a)) = Ax(a + nh), where A is a constant square matrix of degree n.

Theorem 14. The solution to the system

()

with initial conditions (25) and (26), that is,

and x(a) = x_a, x₀, x_a ∈ ℝ^N, is given by the following formula:

()

for n ∈ ℕ₀.

Proof. Notice that for n = 0 we get x(a + 0 · h) = A⁰(φ_0,0(0)x_a + φ_1,0(−h)x₀). Since φ_0,0(0) = 1 and φ_1,0(−h) = 0, we get x(a + 0 · h) = x_a.

For n > 0 let us define the sequence in the following way:

()

where

and

with x₀(a + nh) = x_a.

We calculate the first step. As , then g₀(nh) = Ax_a( ₀Δ^−β1)(b + nh) = Ax_aφ_0,1((n − 1)h). Going further,

()

which could be written as

()

and, using Proposition 11, we get

()

Taking m tending to +∞ we get formula (41) as the solution of (39) and (40) with initial conditions (25) and (26).

3.1. Semilinear Sequential Systems

Firstly we state a technical lemma and notations.

Lemma 15. Let γ : (hℕ) ₀ → ℝ and α > 0. Let and for k ∈ ℕ₁. Then for k ∈ ℕ₁ one gets

()

where t = αh + nh.

Proof. First let us consider the case k = 1. Then from Proposition 12 we can write

()

where t = 2αh + nh, n ∈ ℕ₀.

Let and . Then

()

Equation (46) for k > 1 follows inductively.

Note that

()

Similar to the procedure presented in the proof of Lemma 15 we can prove that for k, s ∈ ℕ₀ and α > 0, β > 0:

()

Taking μ = kα + sβ and using formula (38) we can write (50) shortly in the following way:

()

Moreover, we can also write direct formula for values

given in (38) for nonlinear problem. In fact using Definition 4 of fractional summation, formula (38) of functions

and Proposition 12 we write (51) as follows:

()

Using the power rule formula for μ = 0 and by Remark 10 we can write the recursive formula for the solution to nonlinear problem given by (23) and (24) and conditions (25) and (26):

()

The given formula (53) also works for n = 0 as

. Then x(a + 0h) = x_a. We can check the next steps:

()

For special semilinear case when f(nh, x(nh + a)) = Ax(nh + a) + γ(nh) we have f(0, x(a)) = Ax(a) + γ(0). Then

()

Theorem 16. The solution to the system

()

with initial conditions (25) and (26), that is,

and x(a) = x_a, x₀, x_a ∈ ℝ^N is given by

()

for n ∈ ℕ₀.

Proof. Note that φ_0,0(0) = 1, φ_1,0(−h) = 0 and φ_k+1,k+1(−h) = 0 for k ≥ 0, so we get x(a + 0h) = x_a.

For n > 0 based on the proof for linear case we can write the solution formula as follows:

()

where τ = (k + 1)(α + β). Then taking into account formulas (50) and (51) we get the form (58) as the solution of (56) and (57) with initial conditions (25) and (26).

4. Positivity

Let be the set of real N × M matrices with the nonnegative entries and .

Based on [8, 31, 32] we consider the following definitions.

Definition 17. The fractional system (23) and (24) is called positive fractional system if and only if for any initial conditions .

Similarly as in [32] we will use the recursive formula (35) to show the positivity of the considered systems. Observe that the systems considered in this paper are of the sequential type while in [32] the sequential systems are not studied. Moreover, the Grünwald-Letnikov operator with the step equal to one is used in [32], whereas we study the systems with the h-differences of Caputo type. So in our case the steps are equal to h.

From [32] we have the following lemma.

Lemma 18. If 0 < α < 1, then , i = 1,2, 3, ….

Moreover, for k ≥ 3 we have .

Using the properties of Euler gamma function one can show that if 0 < α + β ≤ 1, then for n ∈ ℕ₁, one has the following inequality:

()

Proposition 19. Let 0 < α + β ≤ 1. If and for all n ≥ 0,

()

then

for all n ≥ 1.

Proof. The proof is by the induction principle. Assume that 0 < α + β ≤ 1 and both α > 0 and β > 0. Since and h > 0, by (35) we have

()

Moreover,

()

where x(a + h) = [x₁(a + h), …, x_N(a + h)] ^T and

. Let x_i(a + nh) and f_i(nh, x(a + nh)) denote the ith coordinates of the vectors x(a + nh) and f(nh, x(a + nh)), respectively. Then since x_i(a + h) ≥ x_i(a) ≥ 0 for i = 1, …, N,

()

Note that for 0 < α + β ≤ 1 we have

, so

. Then since x_i(a) ≥ 0 and (61) holds for n = 0, we get

()

For n = 1 we have

()

Since

, x_i(a + h) ≥ x_i(a) ≥ 0 for i = 1, …, N, and (61) holds for n = 1, we have

()

for 0 < α, β ≤ 1.

Now for n = 2 we get

()

Since

for 0 < α, β ≤ 1, x_i(a + h) ≥ x_i(a) ≥ 0 for i = 1, …, N, and (61) holds for n = 2, using (60) we have

()

for 0 < α, β ≤ 1.

Assume that

for k = 1,2, 3, …, n + 1. Using the properties of gamma function one can show that

for n ≥ 3. Then applying x(a + h) ≥ x(a) to (35) we get for n ≥ 3

()

By inequality (60) and the assumptions, that is,

, k ≤ n + 1, and by (61) one gets

. Hence using the induction principle we get that

for all n ≥ 1.

Corollary 20. Let 0 < α + β ≤ 1 and I_N denote the identity matrix. If and for all n ≥ 1,

()

then

for all n ≥ 1 that is, (39) and (40) is positive.

Remark 21. In [32] the sufficient condition concerning the positivity of the linear discrete systems with Grünwald-Letnikov operator is as follows: . In our case since we have systems with the sequential fractional h-difference, in our condition h and both orders α and β appear. Note that taking h = 1 the sufficient condition (71) has the form .

Let us now consider some examples that illustrate the solution of the considered systems.

Example 22. Let N = 2, α = 0.4, β = 0.5 and h = 0.01. Then let us take a = −0.006 and b = −0.005 and consider the linear system with sequential difference in the following form:

()

with initial conditions (25) and (26), that is,

and x(a) = x_a, x₀, x_a ∈ ℝ². Moreover let

and

. Then the matrix

has nonnegative values and the fact of staring from nonnegative initial conditions provides the remaining in the same positive cone. In Figure 1 we present the trajectory for T = 500 steps on the (x₁, x₂)-plane that start from x_a = (0,0.1) and with the initial value x₀ = (0,1). Let us notice that in the case

one can see that in a few initial steps points are escaping from the positive area (see Figure 2). All calculations were done in the Maple program.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Consider the following system , , where A is given in Example 22, with initial conditions: x₀ = (0,1), x_a = (0,0.1), .

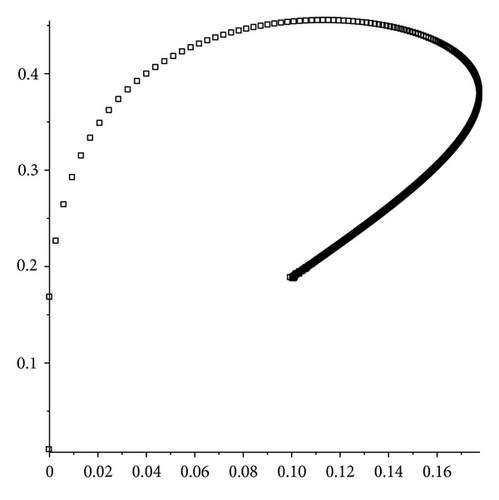
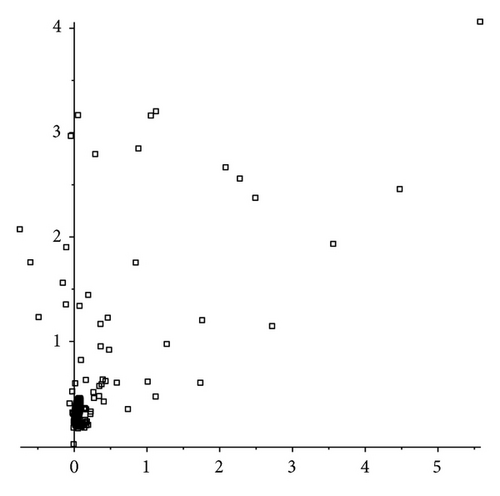
5. Conclusions

The behaviour of the solutions of systems with sequential fractional difference is studied. We present recursive formulas for nonlinear systems and give the exact formulas for the unique solutions to systems in linear and semilinear cases. We prove the sufficient condition for the positivity of considered systems.

Our future goal is to study stability of systems with sequential fractional differences.

Acknowledgments

This project was supported by the foundayion of the National Science Centre granted on the bases of the decision. The DEC-2011/03/B/ST7/03476. This work was supported by Bialystok University of Technology Grant no. G/WM/3/2012.

References

1 Machado J. A. T., Analysis and design of fractional-order digital control systems, Systems Analysis Modelling Simulation. (1997) 27, no. 2-3, 107–122, 2-s2.0-0030651602.
Google Scholar
2 Abdeljawad T. and Baleanu D., Fractional differences and integration by parts, Journal of Computational Analysis and Applications. (2011) 13, no. 3, 574–582, MR2752428, ZBL1225.39008.
Google Scholar
3 Atıcı F. M. and Eloe P. W., A transform method in discrete fractional calculus, International Journal of Difference Equations. (2007) 2, no. 2, 165–176, MR2493595.
Google Scholar
4 Atıcı F. M. and Eloe P. W., Initial value problems in discrete fractional calculus, Proceedings of the American Mathematical Society. (2009) 137, no. 3, 981–989, https://doi.org/10.1090/S0002-9939-08-09626-3, MR2457438, ZBL1166.39005.
10.1090/S0002-9939-08-09626-3
Web of Science® Google Scholar
5 Bastos N. R. O., Ferreira R. A. C., and Torres D. F. M., Discrete-time fractional variational problems, Signal Processing. (2011) 91, no. 3, 513–524, 2-s2.0-78049333168, https://doi.org/10.1016/j.sigpro.2010.05.001.
10.1016/j.sigpro.2010.05.001
Web of Science® Google Scholar
6 Chen F., Luo X., and Zhou Y., Existence results for nonlinear fractional difference equation, Advances in Difference Equations. (2011) 2011, 12, 713201, MR2747089, ZBL1207.39012, https://doi.org/10.1155/2011/713201.
10.1155/2011/713201
Google Scholar
7 Holm M. T., The theory of discrete fractional calculus: development and application [Ph.D. thesis], 2011, University of Nebraska, Lincoln, Neb, USA.
Google Scholar
8 Kaczorek T., Fractional positive continuous-time linear systems and their reachability, International Journal of Applied Mathematics and Computer Science. (2008) 18, no. 2, 223–228, https://doi.org/10.2478/v10006-008-0020-0, MR2426576, ZBL1235.34019.
10.2478/v10006-008-0020-0
Web of Science® Google Scholar
9 Miller K. S. and Ross B., Fractional difference calculus, Proceedings of the International Symposium on Univalent Functions, Fractional Calculus and Their Applications, 1988, Kōriyama, Japan, Nihon University, 139–152.
Google Scholar
10 Mozyrska D. and Girejko E., Overview of the fractional h-difference operators, Advances in Harmonic Analysis and Operator Theory, 2013, 229, Springer, New York, NY, USA, 253–268, Operator Theory: Advances and Applications, https://doi.org/10.1007/978-3-0348-0516-2_14, MR3060418.
Google Scholar
11 Ortigueira M. D., Fractional discrete-time linear systems, 3, Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP ′97), 1997, Munich, Germany, IEEE Computer Society, 2241–2244, https://doi.org/10.1109/ICASSP.1997.599497.
10.1109/ICASSP.1997.599497
Google Scholar
12 Podlubny I., Fractional Differential Equations, 1999, Academic Press, San Diego, Calif, USA, MR1658022.
Web of Science® Google Scholar
13 Abdeljawad T., Dual identities in fractional difference calculus within Riemann, Advances in Difference Equations. (2013) 2013, no. article 36, https://doi.org/10.1186/1687-1847-2013-36, MR3031588.
10.1186/1687-1847-2013-36
Google Scholar
14 Abdeljawad T., On delta and nabla Caputo fractional differences and dual identities, Discrete Dynamics in Nature and Society. (2013) 2013, 12, 406910, https://doi.org/10.1155/2013/406910.
10.1155/2013/406910
Web of Science® Google Scholar
15 Abdeljawad T., Baleanu D., Jarad F., and Agarwal R., Fractional sums and difference with binomial coefficients, Discrete Dynamic Systems in Nature and Society. (2013) 2013, 6, 104173, https://doi.org/10.1155/2013/104173.
10.1155/2013/104173
Web of Science® Google Scholar
16 Ferreira R. A. C. and Torres D. F. M., Fractional h-difference equations arising from the calculus of variations, Applicable Analysis and Discrete Mathematics. (2011) 5, no. 1, 110–121, https://doi.org/10.2298/AADM110131002F, MR2809039.
10.2298/AADM110131002F
Web of Science® Google Scholar
17 Bastos N. R. O., Ferreira R. A. C., and Torres D. F. M., Necessary optimality conditions for fractional difference problems of the calculus of variations, Discrete and Continuous Dynamical Systems. (2011) 29, no. 2, 417–437, https://doi.org/10.3934/dcds.2011.29.417, MR2728463, ZBL1209.49020.
10.3934/dcds.2011.29.417
Web of Science® Google Scholar
18 Mozyrska D. and Pawłuszewicz E., Fractional discrete-time linear control systems with initialisation, International Journal of Control. (2012) 85, no. 2, 213–219, https://doi.org/10.1080/00207179.2011.643413, MR2877340.
10.1080/00207179.2011.643413
Web of Science® Google Scholar
19 Mozyrska D., Girejko E., and Wyrwas M., W. Mitkowski, J. Kacprzyk, and J. Baranowski, Comparison of h-difference fractional operators, Advances in the Thoery and Applications of Non-Integer Order Systems, 2013, 257, Springer, New York, NY, USA, 191–197, Lecture Notes in Electrical Engineering.
Google Scholar
20 Jarad F., Abdeljawad T., Baleanu D., and Biçen K., On the stability of some discrete fractional nonautonomous systems, Abstract and Applied Analysis. (2012) 2012, 9, 476581, https://doi.org/10.1155/2012/476581, MR2889092, ZBL1235.93206.
10.1155/2012/476581
Google Scholar
21 Mozyrska D. and Pawluszewicz E., Local controllability of nonlinear discrete-time fractional order systems, Bulletin of the Polish Academy of Sciences: Technical Sciences. (2013) 61, no. 1, 251–256, https://doi.org/10.2478/bpasts-2013-0024.
10.2478/bpasts-2013-0024
Web of Science® Google Scholar
22 Mozyrska D. and Pawluszewicz E., Controllability of h-difference linear control systems with two fractional orders, International Journal of Systems Science. (2013) https://doi.org/10.1080/00207721.2013.794907.
10.1080/00207721.2013.794907
Web of Science® Google Scholar
23 Pawluszewicz E. and Mozyrska D., W. Mitkowski, J. Kacprzyk, and J. Baranowski, Constrained controllability of h-difference linear systems with two fractional orders, Advances in the Theory and Applications of Non-Integer Order Systems, 2013, 257, Springer, New York, NY, USA, 67–75, Lecture Notes in Electrical Engineering, https://doi.org/10.1007/978-3-319-00933-9_6.
Google Scholar
24 Wyrwas M., Girejko E., Mozyrska D., and Pawłuszewicz E., W. Mitkowski, J. Kacprzyk, and J. Baranowski, Stability of fractional difference systems with two orders, Advances in the Thoery and Applications of Non-Integer Order Systems, 2013, 257, Springer, New York, NY, USA, 41–52, Lecture Notes in Electrical Engineering, https://doi.org/10.1007/978-3-319-00933-9_4.
Google Scholar
25 Miller K. S. and Ross B., An Introduction to the Fractional Calculus and Fractional Differential Equations, 1993, 1st edition, John Wiley & Sons, New York, NY, USA, MR1219954.
Google Scholar
26 Klimek M., Sequential fractional differential equations with hadamard derivative, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 12, 4689–4697, https://doi.org/10.1016/j.cnsns.2011.01.018, MR2820858, ZBL1242.34009.
10.1016/j.cnsns.2011.01.018
Web of Science® Google Scholar
27 Furati K. M., A Cauchy-type problem with a sequential fractional derivative in the space of continuous functions, Boundary Value Problems. (2012) 2012, no. article 58, https://doi.org/10.1186/1687-2770-2012-58.
10.1186/1687-2770-2012-58
Google Scholar
28 Mozyrska D., Girejko E., and Wyrwas M., Fractional nonlinear systems with sequential operators, Central European Journal of Physics. (2013) https://doi.org/10.2478/s11534-013-0223-3.
10.2478/s11534-013-0223-3
Google Scholar
29 Kaczorek T., Reachability and controllability to zero tests for standard and positive fractional discrete-time systems, Journal Européan des Systemès Automatisés. (2008) 42, no. 6–8, 769–787, 2-s2.0-70349613500, https://doi.org/10.3166/JESA.42.769-787.
10.3166/JESA.42.769-787
Google Scholar
30 Kaczorek T., Fractional positive linear systems, Kybernetes. (2009) 38, no. 7-8, 1059–1078, https://doi.org/10.1108/03684920910976826, MR2597223, ZBL1173.93017.
10.1108/03684920910976826
Web of Science® Google Scholar
31 Kaczorek T., Reachability of cone fractional continuous-time linear systems, International Journal of Applied Mathematics and Computer Science. (2009) 19, no. 1, 89–93, https://doi.org/10.2478/v10006-009-0008-4, MR2515026, ZBL1169.93004.
10.2478/v10006-009-0008-4
Web of Science® Google Scholar
32 Kaczorek T., Selected Problems of Fractional Systems Theory, 2011, 411, Springer, Berlin, Germany.
10.1007/978-3-642-20502-6
Web of Science® Google Scholar
33 Abdeljawad T., On Riemann and Caputo fractional differences, Computers & Mathematics with Applications. (2011) 62, no. 3, 1602–1611, https://doi.org/10.1016/j.camwa.2011.03.036, MR2824747, ZBL1228.26008.
10.1016/j.camwa.2011.03.036
Web of Science® Google Scholar

Citing Literature

All articles

On Solutions to Fractional Discrete Systems with Sequential h-Differences

Abstract

1. Introduction

2. Preliminaries

3. Solutions of Systems with Sequential Fractional Differences

3.1. Semilinear Sequential Systems

4. Positivity

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

On Solutions to Fractional Discrete Systems with Sequential h-Differences

Abstract

1. Introduction

2. Preliminaries

3. Solutions of Systems with Sequential Fractional Differences

3.1. Semilinear Sequential Systems

4. Positivity

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information