Volume 2013, Issue 1 382762

Research Article

Open Access

Asymptotic Hyperstability of a Class of Linear Systems under Impulsive Controls Subject to an Integral Popovian Constraint

Corresponding Author

M. De la Sen

[email protected]

Department of Electricity and Electronics, Institute of Research and Development of Processes, University of Basque Country, Campus of Leioa (Bizkaia), Apartado 644, 48940 Bilbao, Spain ehu.es

Search for more papers by this author

A. Ibeas,

A. Ibeas

Department of Telecommunications and Systems Engineering, Universitat Autònoma de Barcelona (UAB), 08193 Barcelona, Spain uab.es

Search for more papers by this author

S. Alonso-Quesada,

S. Alonso-Quesada

Department of Electricity and Electronics, Institute of Research and Development of Processes, University of Basque Country, Campus of Leioa (Bizkaia), Apartado 644, 48940 Bilbao, Spain ehu.es

Search for more papers by this author

M. De la Sen,

Corresponding Author

M. De la Sen

[email protected]

Department of Electricity and Electronics, Institute of Research and Development of Processes, University of Basque Country, Campus of Leioa (Bizkaia), Apartado 644, 48940 Bilbao, Spain ehu.es

Search for more papers by this author

A. Ibeas,

A. Ibeas

Department of Telecommunications and Systems Engineering, Universitat Autònoma de Barcelona (UAB), 08193 Barcelona, Spain uab.es

Search for more papers by this author

S. Alonso-Quesada,

S. Alonso-Quesada

Department of Electricity and Electronics, Institute of Research and Development of Processes, University of Basque Country, Campus of Leioa (Bizkaia), Apartado 644, 48940 Bilbao, Spain ehu.es

Search for more papers by this author

First published: 02 October 2013

https://doi.org/10.1155/2013/382762

Citations: 2

Academic Editor: Hamid Reza Karimi

Share a link

Email
Wechat
Bluesky

Abstract

This paper is focused on the study of the important property of the asymptotic hyperstability of a class of continuous-time dynamic systems. The presence of a parallel connection of a strictly stable subsystem to an asymptotically hyperstable one in the feed-forward loop is allowed while it has also admitted the generation of a finite or infinite number of impulsive control actions which can be combined with a general form of nonimpulsive controls. The asymptotic hyperstability property is guaranteed under a set of sufficiency-type conditions for the impulsive controls.

1. Introduction

The problems of absolute stability and hyperstability classically received much attention from the fifties in a wide class of problems of control theory and its applications, [1–10]. Some extensions or applications of hyperstability theory rely on the incorporation of the formalism of quantified controls [3] and multiple nonlinearities, [4]. Also, in some of the studies, the incorporation of extra subsystems to the linear positive real part, the presence of delays, and that of hybrid continuous-discrete systems has also been considered, [5–7]. Its extension to some models based on neural networks has been studied in [9] and references therein, while its usefulness for the design of adaptive schemes with good stability and transient properties was proposed in a set of results compiled in [10] and in more exhaustive later investigations performed along the eighties and nineties. The properties of parametrical stability of nonlinear systems with some robustness extensions have been investigated in [11, 12] and references therein. Also, applications of stability theory to base-isolated building structures including modelling delays and wireless control issues has been investigated in a number of papers. The main objective of the studies is to prevent the structures via active control designs against earthquake or heavy wind potential damages. See, for instance, [13, 14] and references therein. In those studies, Lyapunov stability and associated appropriate manipulations via linear matrix inequalities are used ad hoc for the problems at hand.

Furthermore, the following Figures 3 and 4 show, respectively, the output and control input to the system.

The problem of absolute stability is basically stated as that of guaranteeing the global asymptotic stability of a control system consisting of a linear plant under a feedback nonlinear regulator which belongs to a certain class of regulators all satisfying either some sector-type or some integral-type constraints of Lurie’s or Popov’s type, respectively. See, for instance, [2–4, 15–17]. If global asymptotic stability is guaranteed for the whole class of regulators then it is typically said that the closed-loop system is absolutely stable for such a class of controllers. The main reason for setting this theory was its ability to guarantee the stabilization for a whole class of systems under potential dispersion of the values of the parameters in a serial controller construction process while keeping its stabilization capability. Thus, it is a robustly stable design for a characterization of the nonlinear feedback controller as belonging to a certain admissible class. Then, the absolute stability property is guaranteed for the feed-forward controlled object and the whole class of nonlinear controllers.

The more general problem of asymptotic hyperstability extends that of absolute stability to classes of nonlinear regulators satisfying integral-type constraints for eventually time-varying nonlinearities which are not necessarily constrained to sectors. The asymptotic hyperstability property of a closed-loop system requires, in particular, that the feed-forward loop consists of a positive real transfer matrix (sometimes referred to as the asymptotic hyperstability of the linear feed-forward loop) or function, and that the nonlinear/time-varying controller belongs to a class satisfying an integral-type constraint, the so-called Popovian integral inequality, [15, 16]. Then, the property is guaranteed for such a linear feed-forward linear block and the whole class of nonlinear/time-varying controllers. Historically, the properties of absolute stability and hyperstability were of crucial interest by the time of World War II because the component dispersion in regulators controlling tanks often fail the blank targeting process, [16]. Such a practical problem motivated the convenience of formulating and designing stabilizing classes of regulators rather than individual stabilizing ones, [15, 16]. The related studies on this subject have been performed for the stabilization of both linear continuous-time and discrete dynamic systems.

Asymptotic hyperstability has also received a very important attention in adaptive control designs such as model reference adaptive control or model reference adaptive systems. See, for instance, [17–25] and references therein. A wide representation of practical problems has been focused on this theoretical formalism including theoretical design of adaptive systems, adaptive control of manipulators and other robotic devices, adaptive neural networks, and synchronization. A main reason of the success of the hyperstability formal theory in the existing background of adaptive designs relies on the fact that the implementation of the estimation algorithms is flexible while offering the designer the chance of choosing wide ranges of admissible values of the free design parameters being compatible with accomplishing the required properties of convergence and closed-loop stabilization.

Most of the stability problems can be extended to the use of switching laws acting on the controlled objects or on their controllers so that the dynamics can be changed to improve certain suitable performances like, for instance, suited settling times or transient errors, or to accommodate the system behavior to suitable transients around several operation points. This frequently happens in complex dynamic problems associated to distinct phases in some production chains like it occurs, for instance, in some chemical engineering processes. Some of such complex models might include point or distributed delays and/or hybrid structures consisting of continuous-time, discrete-time, and digitally modelled subsystems. The existing background literature on switching dynamics is exhaustive. See, for instance, [26–29] and references therein. Finally, recent work on absolute stability and hyperstability of complex nonlinear models, including absolute stability of hyperbolic systems and topics related to Ulam’s-type stability, has been reported in [30–32] and some of the references therein.

Other topics of increasing interest in the last years and nowadays in stabilization and control of dynamic systems are that of the synthesis of impulsive controls and that of the switching conditions of the dynamics guaranteeing the closed-loop stabilization. In particular, the injection of impulsive controls lead to a discontinuous sudden change (in practice, in a very short time interval) in the state vector at impulsive time instants. Switched dynamic systems have several possible parameterizations while switches among them in such a way that the dynamic system is parameterized by one of such parameterizations in connected time-intervals before the next switching happens. It is of interest the design of switching laws which ensure closed-loop stabilization either conditionally, via appropriate rules either on the minimum residence time or on the averaging dwelling times, or under arbitrary switching. Exhaustive work has been made in this field. See, for instance, [26–30, 33–39] and references therein. Related studies are of interest, for instance, in synchronization, deterministic, and stochastic stabilization, impulsive vaccination in epidemic models, control of chemical process under their various dynamics, and so forth. Switched dynamic systems and impulsive control also appear in some combined problems. See, for instance, [27, 38–40] and references therein.

This paper is focused on an extended study of asymptotic hyperstability in the continuous-time framework for a single-input single-output system. Basically, the undertaken generalizations are:

(a)
it has admitted the presence of a parallel connection of a linear strictly proper and strictly stable subsystem to the standard linear asymptotically hyperstable subsystem in the feed-forward loop of the feedback system;
(b)
the generation of a finite or infinite number of impulsive control actions is allowed while it can be combined with a general form of nonimpulsive controls. The control impulses can be state/output dependent or not.

The asymptotic hyperstability property is guaranteed to hold under sufficiency-type conditions for the above proposed general structure. The property is guaranteed under conditions being dependent on certain combined constraints. Such constraints involve the values of the gain of the feed-forward strictly positive real transfer function at infinity, the maximum value of the modulus of its parallel-connected linear block, and the sign and gain bounds of the different impulses of the impulsive control. The paper is organized as follows. Section 2 is devoted to the problem statement and some preliminary results while the main asymptotic hyperstability results are stated and commented in Section 3. The proofs are given in Appendices. Section 4 considers some extensions for robust hyperstability due to the presence of state and measurement disturbances. Section 5 presents some illustrative simulated examples and, finally, conclusions end the main body of the paper.

2. Problem Statement and Some Preliminary Results

Consider the following linear and time-invariant system:

()

which is subject to a potentially nonlinear time-varying controller device satisfying the Popovian type integral inequality below:

()

where x(t) ∈ Rⁿ is the n-state vector, and y(t) and u_im(t) are the output and the (in general, impulsive) control which satisfies the Popovian integral constraint

and any nonzero γ ∈ R. The, in general, nonlinear function φ(y(t), t) used to generate the control input, subject to the integral constraint (4), defines a class of regulators via such a constraint which is admissible to control the linear plant (1) and (3). Thus, the hyperstability property to be addressed in the paper ensures the closed-loop stability for any member of such a class of regulators. Note that if (4) holds for any nonzero γ then it also holds for any γ^′ ≥ γ. The transfer function of the linear feed-forward loop (1)–(3) is decomposed in parallel blocks as follows:

()

where

(i)
is both strictly stable and strictly proper with poles in Re s ≤ −σ < 0 for some σ ∈ R₊ and satisfying for some nonnegative real constant and all ω ∈ R₀₊. Note that its real part is finitely lower-bounded since it is strictly stable.
(ii)
G^*(s) is strictly positive real with d^* = d₀ = lim _ω→±∞G(iω) = lim _ω→±∞G^*(iω) > 0, since, whereis the complex unit andis strictly proper and strictly stable since G^*(s) is strictly positive real and d₀ is a positive real constant.

Note that

is strictly proper and strictly stable since G^*(s) is of zero relative degree (i.e., biproper) since d^*is nonzero. It is well-known that a transfer function G^*(s) is strictly positive (resp., positive real) real if Re G(s) > 0 (resp., Re G(s) ≥ 0) for any complex number s with Re s ≥ 0 (resp., for Re s > 0), and then, it has a relative degree equal to 0 or 1. The sets of strictly positive real and positive real transfer functions are simply denoted in the sequel by SPR and PR, respectively. Strictly positive real transfer functions are strictly stable while the positive real transfer functions are stable. Note that the set of positive real functions contains that of strictly positive real ones. If the transfer functions are realizable, then it is evident that they have relative degrees (also often referred to as relative orders, equivalently, and their pole-zero excess number) being 0 or 1. Now, assume that the impulsive control is of the following form:

()

where u(t) is the piecewise continuous impulse-free input, δ(t) is the Dirac distribution describing the impulsive actions of amplitudes K_jg(t_j) where g(t_j) = 1 if the input impulse is independent of the output and g(t_j) = y(t_j) in the case that it depends directly on such an output. The sequence {g(t_j)} can be, in general, any nonzero function sequence being dependent on the output and input sequences {y(t_j)} and {u(t_j)} at the impulsive time instants. A typical case in many practical situations is that the input impulse is

, that is, g(t_j) = y(t_j). In the following, the subsequent notation is used:

(i)
if τ ∈ [t₁, t₂) and, otherwise, it is a truncated function of f(t) (f_0,t(τ) ≡ f_t(τ) is used for notation abbreviation);
(ii)
Im (t) = {t₁, t₂, …, t_p(t)} is the set of impulsive time instants until time t with the convention t_p(t) < t so that Im (t⁺) = {t₁, t₂, …, t_p+1(t) = t} if t, itself, is an impulsive time instant which is denoted by t ∈ Im (t⁺). Note that the convention implies that if t ∉ Im (t⁺) then Im (t⁺) = Im (t) and that t_k ∉ Im (t_k). Let us also denoteas the whole set of impulsive time instants and card Im_∞ is its cardinal. The notation card Im_∞ = χ₀ (the usual symbol for an infinite cardinal of a numerable set) refers to the case when the set of impulses is infinity while card Im_∞ < χ₀ indicates that there is a finite number of impulses.

The notation “support sequence” for {g(t_j)}, t_j ∈ Im_∞ for some impulsive set Im_∞ is often used by obvious reasons for such a sequence {g(t_j)}.

The limit notationused in some of the obtained results stands for the limits as time tends to infinity within the interimpulse time intervals provided that they exist. In this context, note that (6) is very general so that the impulses can be state-dependent or not. Thus, such limits do not always exist as time tends to infinity to the left of the impulsive time instants. This motivate the use of such a notation.

The following definitions are well-known from the background literature for the impulsive-free case u_im(t) = u(t) in (6).

Definition 1. The closed-loop system (1)–(4) is said to be asymptotically hyperstable (resp., hyperstable) for the impulsive-free case u_im(t) = u(t) for all t ∈ R₀₊ if it is globally asymptotically stable (resp., globally stable) for any control device satisfying Popov’s integral inequalityand any nonzero γ ∈ R₊.

It is well-known that the system (1)–(4) is asymptotically hyperstable if and only if its associate transfer function G(s) ∈ SPR. Note that if G(s) is strongly strictly positive real, since

is strictly proper, then

()

The following preliminary technical results to be then used to establish the main asymptotic hyperstability results hold.

Lemma 2. The input-output energy measure on the time intervals [0, t), respectively, on , respectively, on [0, t] is uniformly bounded for all time while it satisfies the following relationships:

()

where

Proof. See Appendix A.

A useful result based on Lemma 2 follows below so as to get the main stability result after establishing the subsequent definition.

Definition 3. Any sequence of impulsive gains {K_j} subject to the following constraints:

()

for some given real function m(t), which satisfies 0 < m(t) < γ² for all t ∈ R₊, and any

such that y(t_k) ≠ 0, is said to be of the class I_gain = I_gain(Im_∞, γ, g) for some given γ ∈ R₊ and for the support sequence {g(t_j)}, t_j ∈ Im_∞.

The feature that if (4) holds for any nonzero γ then it also holds for any γ^′ ≥ γ makes that the particular value of any finite nonzero γ in (10) can be increased to upper-bound the admissible impulsive gains for different controls while keeping the validity of the formulated asymptotic hyperstability theorem for the impulsive case. See Theorem 10 in Section 3.

Definition 4. An integral Popovian inequality (4) for a nonzero real constant γ and an impulsive control is said to be impulsive control-compatible if the sequence of impulsive gains {K_j} is of the class I_gain(Im_∞, γ, g) for some γ ∈ R₊.

Lemma 5. Assume that the sequence of impulsive gains for system (1)–(4) is of the class I_gain = I_gain(Im_∞, γ, g), then, the following properties hold:

()

if card Im_∞ < χ₀, and

()

if card Im_∞ ≤ χ₀ so that the input-output energy is positive and uniformly upper-bounded by a finite bound for all nonzero time.

Proof. See Appendix B.

Remark 6. It is then proven in Theorem 10 that (11) holds even if card Im_∞ = χ₀ and .

Lemma 5 is subject to the subsequent important necessary condition.

Lemma 7. Assume thatthen a necessary condition for Lemma 5 to hold is that the class I_gain = I_gain(Im_∞, γ, g ) is such that t₁ = 0 ∈ Im(t) ⊂ Im_∞ for all t ∈ R₀₊, and its associate impulsive gain satisfies the constraint:

()

Another necessary condition for Lemma 5 to hold is that the class I_gain = I_gain(Im_∞, γ, g) has an impulsive set of time instants Im_∞ of infinite cardinal.

Proof. Proceed by contradiction by assuming that , Im_∞∋t₁ > 0, and Lemma 5 holds so that (12) holds. Then,

()

and the previous second relationship is clearly a contradiction to t₁ > 0. On the other hand, if there is a finite number of impulsive time instants then the following contradiction follows from (12):

()

Hence, the proof of the result is complete.

To the light of Definition 3, the hyperstability concepts of Definition 1 are extended so as to consider also certain classes on impulsive controls which lead to the global asymptotic stability of the closed-loop system as follows.

Definition 8. The impulsive closed-loop system (1)–(4) is said to be impulsive asymptotically I_gain(Im_∞, γ, g)-hyperstable (resp., impulsive I_gain(Im_∞, γ, g)-hyperstable) if it is globally asymptotically stable (resp., globally stable) for any sequence of impulsive gains {K_j} of the class I_gain = I_gain(Im_∞, γ, g) for a given nonzero γ ∈ R₊, a given support sequence {g(t_j)}, t_j ∈ Im_∞, and any control device satisfying an impulsive control compatible Popov’s integral inequality.

3. Main Results on Asymptotic Hyperstability

It turns out that Lemma 7 establishes that the origin has to be an impulsive time instant to keep the input-output energy to be positive and upper-bounded for all time. On the other hand, Lemma 5 leads to the subsequent main result of usefulness in the impulsive-free case.

Theorem 9. Assume that Im_∞ = ∅ (i.e., there are no impulsive controls). Then, the following properties hold.

(i)
Assume also that G^*(s) ∈ SPR and. Then, ∞ > E(t) ≥ 0 for all t ∈ R₀₊ with E(0) = 0, and the closed-loop system is asymptotically hyperstable for any nonlinear feedback device φ(y(t), t) satisfying Popov’s integral inequality for all t ∈ R₀₊. As a result, G(s) ∈ SPR, lim _t→∞u(t) = 0, u(t), y(t) and x(t) are uniformly bounded for all t ∈ R₀₊, and lim _t→∞y(t) = 0 and lim _t→∞x(t) = 0 for all x₀ ∈ Rⁿ.
(ii)
Assume that Re G^*(iω) > 0, for all ω ∈ R₀₊, and.

Then, Lemma 5 holds and the closed-loop system is asymptotically hyperstable for any nonlinear feedback device φ(y(t), t) satisfying Popov’s integral inequality

for all t ∈ R₀₊. The, lim _t→∞u(t) = 0, u(t), y(t) and x(t) are uniformly bounded for all t ∈ R₀₊, and lim _t→∞y(t) = 0 and lim _t→∞x(t) = 0 for all x₀ ∈ Rⁿ.

Proof. It is given in Appendix C.

Theorem 9(i) addresses the asymptotic hyperstability for the impulsive-free case when G^*(s) ∈ SPR is strongly positive real since G^*(iω) ≥ d > 0 for all ω ∈ R₀₊. Theorem 9(ii) considers the same property for the case when G^*(s) ∈ SPR is weakly positive real since G^*(iω) > 0 and d = lim _ω→±∞G^*(iω) = 0, that is, the transfer function is strictly proper so that it is zero at infinity frequency. Lemma 5 leads to the subsequent main result of usefulness in the control impulsive case.

Theorem 10. Assume that card Im_∞ ≤ χ₀ (i.e., there are impulsive controls with χ₀ being the infinity cardinal of a denumerable set) for any set of control impulses of amplitudes satisfying (10). Then, the following properties hold.

(i)
Assume also that G(s) ∈ SPR with . Then, ∞ > E(t) ≥ 0 for all t ∈ R₀₊ with E(0) = 0, and the closed-loop system is impulsive asymptotically I_gain(Im_∞, γ, g)-hyperstable for any nonlinear feedback device φ(y(t), t) satisfying a compatible Popov’s integral inequality for all t ∈ R₀₊. As a result, y(t) and x(t) are uniformly bounded for all t ∈ R₀₊ for all x₀ ∈ Rⁿ, u(t) is bounded for t ∈ R₀₊∖Im_∞, with if card Im_∞ = χ₀ (i.e., there are infinitely many control impulsive time instants); and lim _t→∞u(t) = 0 if card Im_∞ < χ₀, that is, if there is a finite number of control impulsive time instants. Also
()
(ii)
Assume that Re G^*(iω) > 0, for all ω ∈ R₀₊ and.

Then, Lemma 5 holds and the closed-loop system is asymptotically hyperstable for any nonlinear feedback device φ(y(t), t) satisfying Popov’s integral inequality

for all t ∈ R₀₊. Then, y(t) and x(t) are uniformly bounded for all t ∈ R₀₊, for all x₀ ∈ Rⁿ, u(t) is bounded for t ∈ R₀₊∖Im_∞, with

if card Im_∞ = χ₀ (i.e., there are infinitely many control impulsive time instants); and lim _t→∞u(t) = 0, lim _t→∞x(t) = 0 and lim _t→∞y(t) = 0 if card Im_∞ < χ₀ (i.e., there is a finite number of control impulsive time instants) or if card Im_∞ = χ₀ (i.e., there are infinitely many control impulsive time instants) and K_j → 0 as j → ∞. Also, the boundedness properties (16) for the impulsive contributions still hold.

Proof. It is given in Appendix D.

Note that the constraint (10) invoked in Theorem 10 is guaranteed by amplitude constraints of each impulse at t_k depending only on input and output values on [0, t_k) for the case of signal-dependent control impulses.

4. Some Extensions Concerning Robustness

Assume that (1) is modified in the presence of state and measurement disturbances η(t) and λ(t), of respective Laplace transforms N(s) and Λ(s), as follows:

()

Taking Laplace transforms under zero initial conditions in (17), one gets

()

where A and A^* are stability matrices with

(then also strictly stable biproper if d₀ = d^* > 0 and strictly proper if d₀ = 0), and

being strictly stable and strictly proper. Now, the results of Sections 2 and 3 can be reformulated for this case with the replacement of the nominal output y(t) by a modified output calculated as follows:

()

where

is the impulse response of c^T(sI − A) ⁻¹. Define the robust impulsive class and its associated robust impulsive I_rgain = I_rgain(Im_∞, γ, g, η, λ )-hyperstability and asymptotic I_rgain = I_rgain(Im_∞, γ, g, η, λ)-hyperstability as follows.

Definition 11. Any sequence of impulsive gains {K_j} subject to the following constraints:

()

for some given real function m(t), which satisfies 0 < m(t) < γ² for all t ∈ R₊, and any

, such that y(t_k) ≠ 0, is said to be of the robust impulsive class I_rgain = I_rgain(Im_∞, γ, g, η, λ) for some given γ ∈ R₊ and for the support sequence {g(t_j)}, t_j ∈ Im_∞.

Definition 12. The impulsive closed-loop system (17), subject to (2), is said to be robustly impulsive asymptotically I_rgain(Im_∞, γ, g, η, λ)-hyperstable (resp., impulsive I_rgain(Im_∞, γ, g, η, λ)-hyperstable) if it is globally asymptotically stable (resp., globally stable) for any sequence of impulsive gains {K_j} of the class I_rgain(Im_∞, γ, g, η, λ) for a given nonzero γ ∈ R₊, a given support sequence {g(t_j)}, t_j ∈ Im_∞ and any control device satisfying an impulsive control compatible Popov integral inequality; for all t ∈ R₀₊.

Now, the asymptotic hyperstability Theorem 10 is directly extended for robust asymptotic hyperstability as follows.

Theorem 13. Assume that card Im_∞ ≤ χ₀ for any set of control impulses of amplitudes satisfying (20). Assume also thatis uniformly bounded for all t ∈ R₀₊ (it suffices that λ(t) and η(t) be bounded for all time). Then, the following properties hold.

(i)
Assume also that G(s) ∈ SPR with . Then, ∞ > E(t) ≥ 0 for all t ∈ R₀₊ with E (0) = 0, and the closed-loop system is robustly impulsive asymptotically I_rgain(Im_∞, γ, g, η, λ)-hyperstable for any nonlinear feedback device φ(y(t), t) satisfying a compatible Popov’s integral inequality for all t ∈ R₀₊. As a result, y(t) and x(t) are uniformly bounded for all t ∈ R₀₊ for all x₀ ∈ Rⁿ, u(t) is bounded for t ∈ R₀₊∖Im_∞, with if card Im_∞ = χ₀ (i.e., there are infinitely many control impulsive time instants); and lim _t→∞u(t) = 0 if card Im_∞ < χ₀ (i.e., there is a finite number of control impulsive time instants).
(ii)
Assume that Re G^*(iω) > 0, for all ω ∈ R₀₊ and.

Then, Lemma 5 holds and the closed-loop system is robustly asymptotically hyperstable for any nonlinear feedback device φ(y(t), t) satisfying Popov’s integral inequality for all t ∈ R₀₊. Then, y(t) and x(t) are uniformly bounded for all t ∈ R₀₊, for all x₀ ∈ Rⁿ, u(t) is bounded for t ∈ R₀₊∖Im_∞, with if card Im_∞ = χ₀ (i.e., there are infinitely many control impulsive time instants); and lim _t→∞u(t) = 0, lim _t→∞x(t) = 0 and lim _t→∞y(t) = 0 if card Im_∞ < χ₀ (i.e., there is a finite number of control impulsive time instants) or if card Im_∞ = χ₀ (i.e., there are infinitely many control impulsive time instants) and K_j → 0 as j → ∞.

Proof (outline). It is given in Appendix E.

5. Numerical Examples

This section discusses some simulation examples illustrating the theoretical results stated in the previous ones. Two different examples will be provided. The first one corresponds to the impulsive-free case while the second one considers the effect of feedback impulses. The following transfer functions are used:

()

G^*(s) is SPR since it is stable and Re G^*(jω) = (4ω² + 30)/(ω⁴ + 29ω² + 100) > 0 for ω ≥ 0. On the other hand,

is stable but is not SPR since its relative degree is two. Therefore,

is a parallel connection of an SPR and a non-SPR transfer function as discussed in Section 2. In addition, a family of nonlinear feedback functions is given by φ_i(y, t) = tanh (γ_iy), where γ_i ∈ {0.2,0.6,1.4}. These nonlinear functions satisfy the integral-type Popov’s constraint specified by (4) since tanh (γ_iy)y > 0 for y ≠ 0, and tanh (γ_iy)y = 0 for y = 0, implying that

for any t > 0 and all i = 1,2, 3. The next Section 5.1 shows the asymptotic hyperstability of the closed-loop for the SPR transfer function G^*(s) and for the non-SPR transfer function G(s) in the absence of impulses. The state variables are always defined from the (minimal) canonical controllable state-space realizations of the transfer functions with the first state component being the output. The initial conditions are in all the cases x₁(0) = 1, x₂(0) = 2.5 for the realization of G^*(s), and x₁(0) = 1, x₂(0) = 2.5, x₃(0) = −1, x₄(0) = 2 for the realization of G(s). We point out that the hyperstability properties of strictly positive real transfer functions are independent of the chosen realization and on the fact that it is minimal or not. Note that, if the realization is nonminimal, it has to be stable and any potential zero-pole cancellations do not modify the frequency plots and then the positive realness properties and minimum gain values.

5.1. Asymptotic Hyperstability in the Impulsive-Free Case

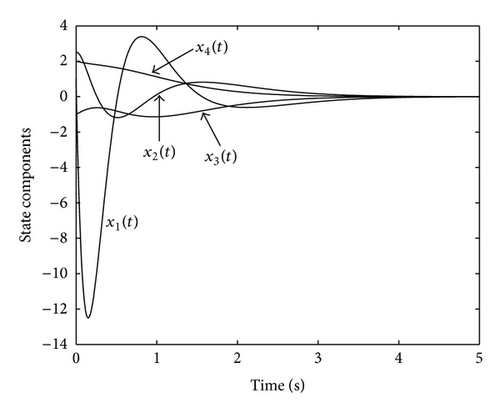
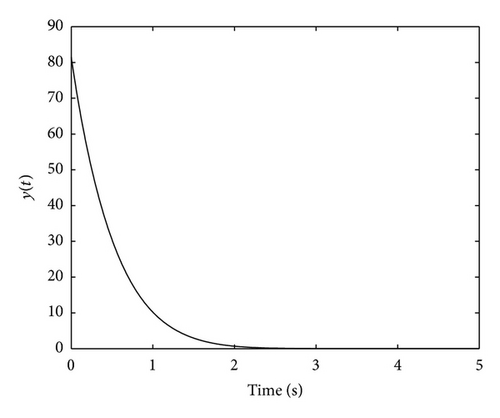
Figures 1 and 2 show the evolution of the state variables of the SPR system G^*(s) when members of the family of nonlinear static feedback devices φ_i(y, t) = tanh (γ_iy) are used as controllers.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Evolution of the state variable x₁(t).

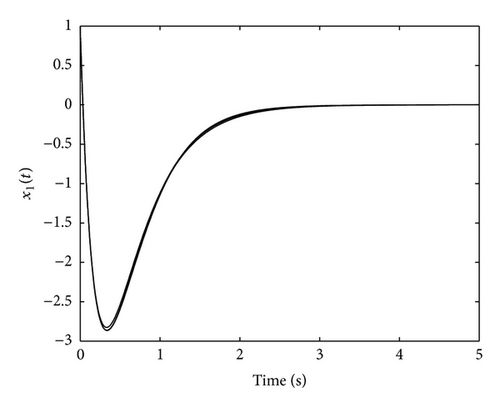
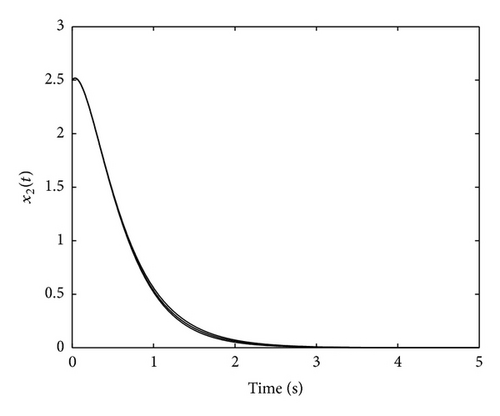
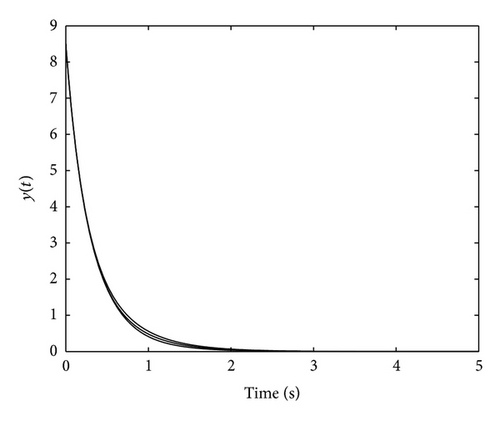
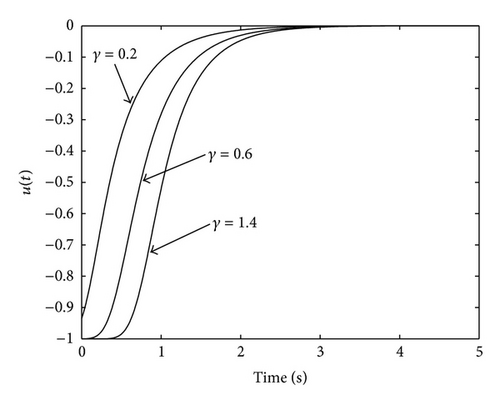
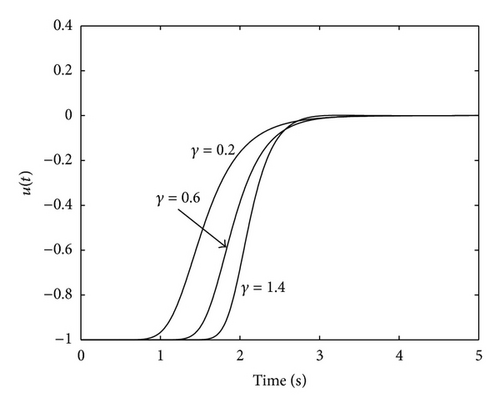
Figures 1–4 confirm the results of Theorem 9(i) guaranteeing the boundedness and convergence to zero of the state, the output and the control signal. Moreover, it can be appreciated in Figures 1–3 that the evolution of the system is very similar for the different considered values of γ_i. This similar evolution is obtained at the expense of a different control action for each γ_i, as Figure 4 depicts. On the other hand, the following Figures 5, 6, and 7 show the state evolution, the output and the control input for the non-SPR system G(s). The particular value of γ_i = 0.6 has been used in Figures 5 and 6 since the evolution of the system is very similar for all values of γ_i. However, Figure 7 shows the control input for different values of γ_i since its value varies depending on γ_i. Figures 5–7 confirm the results of Theorem 9(ii) guaranteeing the convergence to zero of the state, the output, and the control signal. The next Section 5.2 is devoted to the study of the impulsive control.

5.2. Asymptotic Hyperstability in the Presence of Impulses

A number of impulses are added to the nonlinear feedback controller introduced in Section 5.1. The support sequence is given by g(t_k) = y(t_k) and the impulsive gains constant K_k = 1. The impulsive time instants are multiples of 0.2 seconds; this means that the presence of impulses is periodic. The value γ_i = 0.6 has been used for the sake of simplicity. Figure 8 depicts the evolution of the state variables of the SPR transfer function G^*(s) while Figure 9 shows the output. Finally, Figure 10 illustrates the control input with the impulsive action.

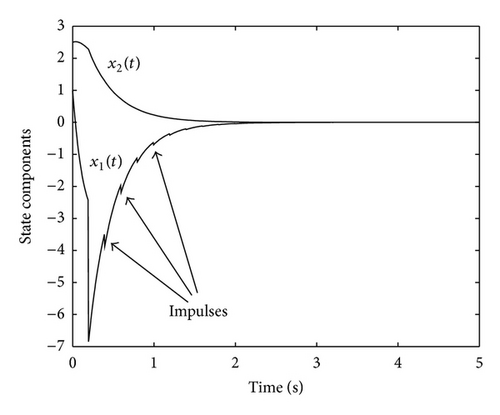
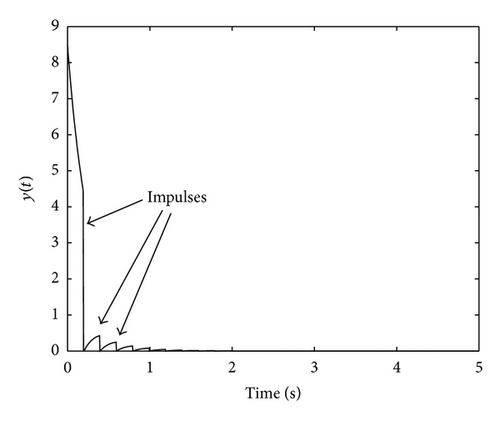
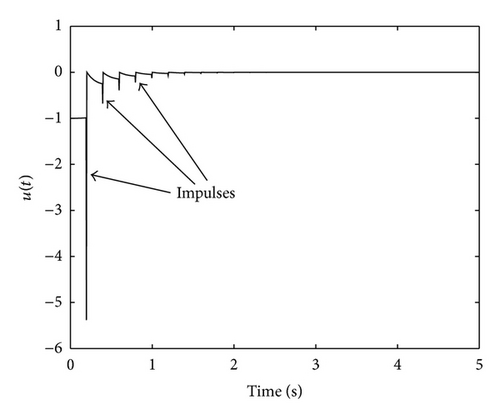
Figures 8–10 confirm the statements of Theorem 10(i) showing the convergence to zero of the state, the output, and the control signal. In addition, these figures explicitly show the presence of impulses in different signals of the system. On the other hand, for the complete system, G(s), we obtain the following Figures 11, 12, 13, and 14 depicting the state evolution, the output, and the control input.

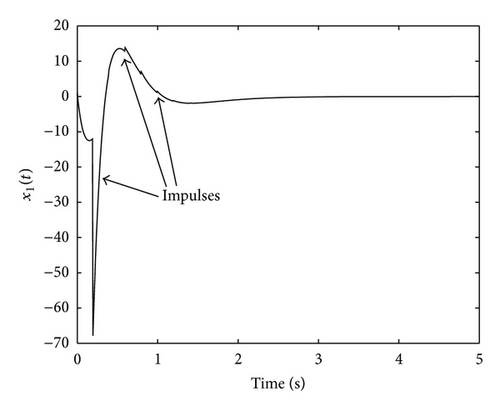
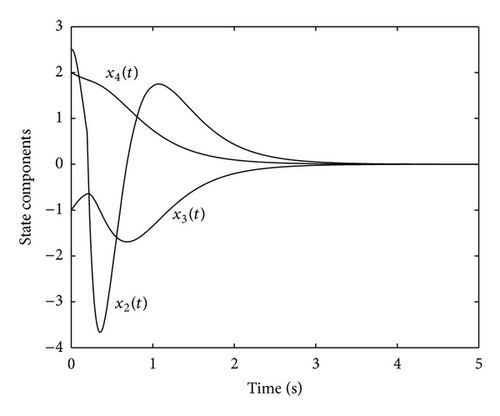
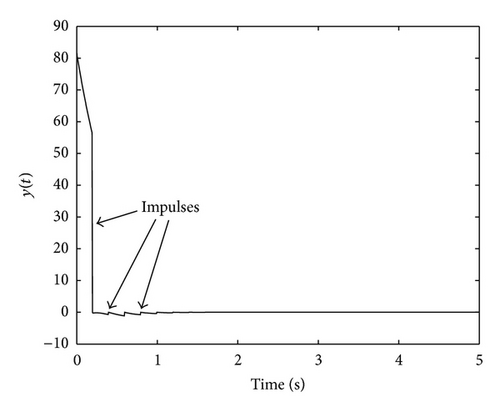
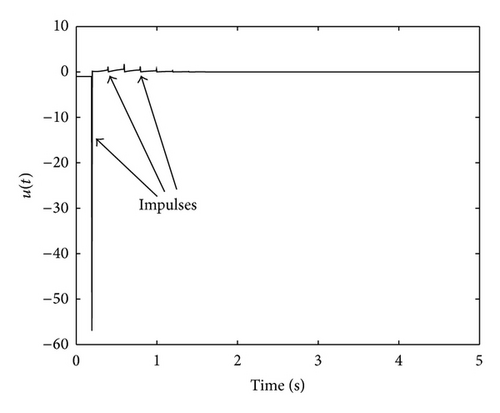
Figures 11–14 illustrate the results compiled in Theorem 10(ii) since they show the convergence of the state, the output and the input to zero. Moreover, it can be appreciated the effect of adding impulses to the control signal by first comparing Figures 3 and 9 and, on the other hand, Figures 6 and 13. It can be deduced that the use of an impulsive controller makes the output to converge to zero faster than when a single continuous-time one is used. This fact highlights how the concept of impulsive asymptotic hyperstability is relevant since it allows ensuring the closed-loop stability for a whole family of nonlinear devices while accelerating the convergence of the output to zero.

6. Conclusions

This paper has studied the problem of asymptotic hyperstability under a regular controller combined with a class of impulsive controls provided that the feed-forward linear- loop is not asymptotically hyperstable, since it has a parallel component subsystem being strictly stable. Asymptotic hyperstability results with robustness extensions have also been discussed. The controller has been assumed to satisfy an integral Popovian-type inequality for all time. Also, examples have been given to illustrate the proposed study.

Acknowledgments

The authors are grateful to the Spanish Government for its support of this research through Grant DPI2012-30651 and to the Basque Government for its support of this research through Grants IT378-10 and SAIOTEK S-PE12UN015. They are also grateful to the University of Basque Country for its financial support through Grant UFI 2011/07. Finally, the authors are very grateful to the reviewers by their useful comments.

Appendices

A. Proof of Lemma 2

The Popovian integral constraints (8)-(9) and Parseval’s theorem while absorbing the delta distribution describing impulses from the time-integral or frequency-integral of the input-output energy measures are used. Then, one gets the following sets of inequalities and equalities by taking into account the use of truncated signals to convert time-integral expressions in frequency ones and vice versa as well as the symmetry of the frequency-response hodographs G^*(iω) and

()

In the same way, and since,

, one has

()

and the proof is complete.

B. Proof of Lemma 5

The finite uniform upper-bound of (12) follows from Lemma 2. It is needed to guarantee a positive lower-bound for all nonzero time so that

()

to hold with

. This implies that

and

while it is avoided that (12) can hold with

. Thus, it suffices for any given strictly positive bounded function 0 < m(t) < γ² for all t ∈ R₊ to guarantee (B.1) in the form

()

or, equivalently,

()

so that (12) holds if card Im_∞ ≤ χ₀ if and only if for each

Consider

()

which holds if (10) holds for any

, such that y(t_k) ≠ 0, which also implies that (11) holds if card Im_∞ < χ₀.

C. Proof of Theorem 9

(i) If Im_∞ = ∅ and

, then also d > 0 as a result, and one has from (B.1) in the proof of Lemma 5 that for any nonzero piecewise continuous control input satisfying Popovian integral inequality the following:

()

The property γ² ≥ E(t) > 0 for all t ∈ R₀₊ with E (0) = 0 follows from (B.1) in view of (A.1). Since u(t) is piecewise continuous then it is also bounded for all time. Thus, since the matrix A is strictly stable, x(t) and y(t) are bounded for all time and also lim _t→∞x(t) = 0, and lim _t→∞y(t) = 0 for any x₀ ∈ Rⁿ with the state and output being also uniformly bounded since

implies that

for all Re s ≥ 0 so that

and then is strictly stable.

(ii) In this case, Im_∞ = ∅. One has from the given hypotheses that

(1)
,
(2)
.

Direct calculations similar to those performed in the proof of Lemma 2 yield

()

where M(W) = min _{ω∈[−W, W]}Re G(iω) and

are everywhere continuous, nonnegative, and strictly decreasing so that lim _W→∞M(W) = lim _W→∞ε_t(W) = 0; for all t ∈ R₀₊. Thus, for a sufficiently large finite W₀ ∈ R⁺ and for all t ∈ R₀₊, (γ² − ε_t(W))/M(W) is finite and positive for all W ≥ W₀ so that

()

The remaining of the proof follows in the same way as that of property (i).

D. Proof of Theorem 10

It follows directly as the proof of Theorem 9 by using Lemma 5 and the guidelines for the proof of Lemma 2 with the following modifications. The control is bounded except at the impulsive time instants while the state and output are uniformly bounded while possessing discontinuities at the impulsive time instants. Furthermore, if card Im_∞ < χ₀, then it is possible to take an initial state after some sufficiently large finite time, which are bounded for any bounded x₀, to conclude that the control, input, and output converge asymptotically to zero as in the impulsive-free case of Theorem 9. To prove that the control, state and output converge to zero as time tends to infinity if card Im_∞ = χ₀ with K_j → 0 as j → ∞, note that

()

as j → ∞, u(t) → 0 since

as j → ∞. Then, x(t) → 0, y(t) → 0 as t → ∞ since A is strictly stable, and

()

and, since K_j → 0 and

as j → ∞, one concludes that

()

Then,

, so that there is a limit

. Then

or it does not exist, which would be contradiction, unless x^* = 0. Then,

and, since A is strictly stable, and u(t) → 0 as t → ∞, x(t) → 0 on [t_j, t_j+1) as t_j → ∞. Since

then x(t) → 0 on

as t_j → ∞. As a result and since t_j → ∞, x(t) → 0 as t → ∞. The same property follows for the output so that y(t) → 0 as t → ∞, and u(t_j) → 0 as t_j → ∞, since if card Im_∞ = χ₀, |t_j+1 − t_j| < ∞ and u(t_j) → 0 as t_j → ∞, then

so that u(t) → 0 as t → ∞ since u(t) is almost everywhere piecewise continuous on its definition domain. It also follows from (12) and (C.3) that

()

so that (11) in Lemma 5 holds, in fact, if card Im_∞ ≤ χ₀ and

. The boundedness of the state and the output for all time follow directly from that of the input and the strict stability of the feed-forward system. The boundedness properties of the impulsive contributions (16) follow from Lemma 2 and (8)-(9), for both properties (i)-(ii).

E. Outline of Proof of Theorem 13

Most of the proof is close to that of Theorem 10. It has to be rearranged as the proof of the validity of (16). One has from (20), the modified property of the boundedness of the input-output energy measure (8) and resulting modified inequalities arising in the proof of Theorem 10 that

()

Then,

is bounded since

is bounded and

()

The rest of the proof follows “mutatis-mutandis” correspondingly to that of Theorem 10.

References

1 Xiong K., Necessary and sufficient conditions for the existence of a Lyapunov function with a quadratic form plus an integral term, International Journal of Control. (1996) 64, no. 4, 707–719, https://doi.org/10.1080/00207179608921651, MR1656782, ZBL0855.93062.
10.1080/00207179608921651
Web of Science® Google Scholar
2 Xu B., Liu X., and Liao X., Absolute stability of Lurie systems with impulsive effects, Computers & Mathematics with Applications. (2004) 47, no. 2-3, 419–425, https://doi.org/10.1016/S0898-1221(04)90034-X, MR2048193, ZBL1057.34049.
10.1016/S0898-1221(04)90034-X
Web of Science® Google Scholar
3 Zhou B., Duan G.-R., and Lam J., On the absolute stability approach to quantized feedback control, Automatica. (2010) 46, no. 2, 337–346, https://doi.org/10.1016/j.automatica.2009.10.039, MR2877078, ZBL1205.93133.
10.1016/j.automatica.2009.10.039
Web of Science® Google Scholar
4 Kazemy A. and Farrokhi M., Robust absolute stability analysis of multiple time-delay Lur′e systems with parametric uncertainties, Asian Journal of Control. (2013) 15, no. 1, 203–213, https://doi.org/10.1002/asjc.503, MR3015769.
10.1002/asjc.503
Web of Science® Google Scholar
5 De la Sen M., Stability of composite systems with an asymptotically hyperstable subsystem, International Journal of Control. (1986) 44, no. 6, 1769–1775, https://doi.org/10.1080/00207178608933701, MR864922, ZBL0606.93059.
10.1080/00207178608933701
Web of Science® Google Scholar
6 De la Sen M., Some conceptual links between dynamic physical systems and operator theory issues concerning energy balances and stability, Informatica. (2005) 16, no. 3, 395–406, MR2168732, ZBL1140.93473.
10.15388/Informatica.2005.106
Web of Science® Google Scholar
7 De la Sen M., On the asymptotic hyperstability of dynamic systems with point delays, IEEE Transactions on Circuits and Systems I. (2003) 50, no. 11, 1486–1488, https://doi.org/10.1109/TCSI.2003.818621, MR2024572.
10.1109/TCSI.2003.818621
Web of Science® Google Scholar
8 Wang D. and Liao F., Absolute stability of Lurie direct control systems with time-varying coefficients and multiple nonlinearities, Applied Mathematics and Computation. (2013) 219, no. 9, 4465–4473, https://doi.org/10.1016/j.amc.2012.10.050, MR3001497.
10.1016/j.amc.2012.10.050
Web of Science® Google Scholar
9 Zeng H.-B., He Y., Wu M., and Xiao S.-P., Absolute stability and stabilization for Lurie networked control systems, International Journal of Robust and Nonlinear Control. (2011) 21, no. 14, 1667–1676, https://doi.org/10.1002/rnc.1658, MR2835694, ZBL1227.93099.
10.1002/rnc.1658
Web of Science® Google Scholar
10 Landau Y. D., Adaptive Control: The Model Reference Approach, 1979, Marcel Dekker, New York, NY, USA, MR535441.
Google Scholar
11 Sundarapandian V., New results on the parametric stability of nonlinear systems, Mathematical and Computer Modelling. (2006) 43, no. 1-2, 9–15, https://doi.org/10.1016/j.mcm.2005.04.010, MR2197399, ZBL1156.34330.
10.1016/j.mcm.2005.04.010
Web of Science® Google Scholar
12 Sundarapandian V., A necessary condition for local asymptotic stability of nonlinear systems with exogenous disturbance, Computers & Mathematics with Applications. (2006) 51, no. 3-4, 667–672, https://doi.org/10.1016/j.camwa.2005.01.032, MR2207450, ZBL1179.93095.
10.1016/j.camwa.2005.01.032
Web of Science® Google Scholar
13 Karimi H. R., Zapateiro M., and Luo N., An LMI approach to vibration control of base-isolated building structures with delayed measurements, International Journal of Systems Science. (2010) 41, no. 12, 1511–1523, https://doi.org/10.1080/00207720903402513, MR2734127, ZBL1206.93050.
10.1080/00207720903402513
Web of Science® Google Scholar
14 Karimi H. R., Luo N., Zapateiro M., and Zhang L., H-infinity control design for building structures under seismic motion with wireless communication, International Journal of Innovative Computing, Information and Control. (2011) 7, no. 9, 5269–5284, 2-s2.0-80052429020.
Web of Science® Google Scholar
15 Landau I. D., Systèmes Non linéaires, Notes de cours, 1975, Laboratoire d'Automatique de Grenoble, ENSGP, Grenoble, France.
Google Scholar
16 Popov V.-M., Hyperstability of Control Systems, 1973, Springer, New York, NY, USA.
10.1007/978-3-642-65654-5
Google Scholar
17 Li R., Liu B., and Liu C., Absolute stability and master-slave synchronization of systems with state-dependent nonlinearities, Mathematical Problems in Engineering. (2013) 2013, 6, 326560, https://doi.org/10.1155/2013/326560.
10.1155/2013/326560
Web of Science® Google Scholar
18 Landau I. D., A generalization of the hyperstability conditions for model reference adaptive systems, IEEE Transactions on Automatic Control. (1972) 17, 246–247, MR0373713.
10.1109/TAC.1972.1099940
Google Scholar
19 Chen F., Hou R., and Tao G., Adaptive controller design for faulty UAVs via quantum information technology, International Journal of Advanced Robotic Systems. (2012) 9, https://doi.org/10.5772/53617.
10.5772/53617
Web of Science® Google Scholar
20 Wang X. and Zhao J., Switching adaptive tracking control of robot manipulators with friction and changing loads, International Journal of Systems Science. (2013) https://doi.org/10.1080/00207721.2013.801098.
10.1080/00207721.2013.801098
Web of Science® Google Scholar
21 Prause F. and Reuter J., A model reference adaptive approach for state estimation in electromagnetic actuators, Proceedings of the 17th IEEE International Conference on Methods and Models in Automation and Robotics (MMAR ′12), 2012, 361–366.
Google Scholar
22 Khalilian M., Abedi A., and Zadeh A. D., Sensorless direct torque control of hybrid stepper motor based on MRAS, Energy Procedia. (2012) 14, 1992–1997.
10.1016/j.egypro.2011.12.1199
Google Scholar
23 Panwar V., Kumar N., Sukavanam N., and Borm J., Adaptive neural controller for cooperative multiple robot manipulator system manipulating a single rigid object, Applied Soft Computing Journal. (2012) 12, no. 1, 216–227, 2-s2.0-81155148255, https://doi.org/10.1016/j.asoc.2011.08.051.
10.1016/j.asoc.2011.08.051
Web of Science® Google Scholar
24 Ulrich S. and Sasiadek J. Z., Modified simple adaptive control for a two-link space robot, Proceedings of the 2010 American Control Conference (ACC ′10), July 2010, 3654–3659, 2-s2.0-77957768341.
Google Scholar
25 Niu Y., Robust passivity and feedback design for nonlinear stochastic systems with structural uncertainty, Mathematical Problems in Engineering. (2013) 2013, 9, 460348, https://doi.org/10.1155/2013/460348.
10.1155/2013/460348
Web of Science® Google Scholar
26 Lien C.-H., Yu K.-W., Chung L.-Y., and Chen J.-D., H-infinity performance for uncertain discrete switched systems with interval time-varying delay via switching signal design, Applied Mathematical Modelling. (2013) 37, no. 4, 2484–2494, https://doi.org/10.1016/j.apm.2012.06.001, MR3002334.
10.1016/j.apm.2012.06.001
Web of Science® Google Scholar
27 Li X., Karimi H. R., and Xiang Z., Robust reliable control of uncertain discrete impulsive switched systems with state delays, Mathematical Problems in Engineering. (2013) 2013, 8, 197819, https://doi.org/10.1155/2013/197819, MR3035652.
10.1155/2013/197819
Web of Science® Google Scholar
28 De la Sen M., Stability of switched feedback time-varying dynamic systems based on the properties of the gap metric for operators, Abstract and Applied Analysis. (2012) 2012, 17, 612198, https://doi.org/10.1155/2012/612198, MR2999874, ZBL1255.93115.
10.1155/2012/612198
Google Scholar
29 De la Sen M. and Ibeas A., Stability results for switched linear systems with constant discrete delays, Mathematical Problems in Engineering. (2008) 2008, 28, 543145, https://doi.org/10.1155/2008/543145, MR2482049, ZBL1162.93393.
10.1155/2008/543145
Web of Science® Google Scholar
30 Tai Z., Wang X., Shi Y., and Karimi H. R., Input-to-state stability of Lur′e hyperbolic distributed complex-valued parameter control systems: LOI approach, Mathematical Problems in Engineering. (2013) 2013, 4, 364057, https://doi.org/10.1155/2008/364057, MR3035636.
10.1155/2013/364057
Web of Science® Google Scholar
31 Brillouët-Belluot N., Brzdęk J., and Ciepliński K., On some recent developments in Ulam′s type stability, Abstract and Applied Analysis. (2012) 2012, 41, 716936, https://doi.org/10.1155/2012/716936, MR2999925, ZBL1259.39019.
10.1155/2012/716936
Google Scholar
32 Fang Y., You X., and Chen Z., New phase fitted and amplification fitted Numerov-type methods for periodic IVPs with two frequencies, Abstract and Applied Analysis. (2012) 2012, 15, 742585, https://doi.org/10.1155/2012/742585, MR2984039, ZBL1253.65110.
10.1155/2012/742585
Google Scholar
33 Zhou X., Liu S., and Jiang W., Complete controllability of impulsive fractional linear time-invariant systems with delay, Abstract and Applied Analysis. (2013) 2013, 7, 374938, https://doi.org/10.1155/2013/374938.
10.1155/2013/374938
Google Scholar
34 Dai X. and Yang F., Complete controllability of impulsive stochastic integrodifferential systems in Hilbert space, Abstract and Applied Analysis. (2013) 2013, 7, 783098, https://doi.org/10.1155/2013/783098.
10.1155/2013/783098
Google Scholar
35 Wu R. and Cao C., Modified projective synchronization of hyper-chaotic systems with nonlinear adaptive-impulsive control, Proceedings of the 25th Chinese Control and Decision Conference (CCDC ′13), May 2013, 440–443.
Google Scholar
36 Chen Y. and Xiang Z., The globally attractivity of a SIV epidemic disease model with two delays and pulse vaccination, Proceedings of the 25th Chinese Control and Decision Conference (CCDC ′13), May 2013, 4416–4420.
Google Scholar
37 de la Sen M., Ibeas A., and Alonso-Quesada S., A time-varying SIS epidemic model with incidence rate depending on the susceptible and infective populations with eventual impulsive effects, Applied Mathematics and Computation. (2013) 219, no. 10, 5516–5536, https://doi.org/10.1016/j.amc.2012.11.001, MR3009508.
10.1016/j.amc.2012.11.001
Web of Science® Google Scholar
38 Li X., Xiang Z., and Karimi H. R., Asynchronously switched control of discrete impulsive switched systems with time delays, Information Sciences. (2013) 249, 132–142.
10.1016/j.ins.2013.06.007
Web of Science® Google Scholar
39 Huang S., Xiang Z., and Karimi H. R., Input-output finite-time stability of discrete-time impulsive switched linear systems with state delays, Circuits, Systems, and Signal Processing. (2013) https://doi.org/10.1007/s00034-013-9610-7.
10.1007/s00034-013-9600-9
Web of Science® Google Scholar
40 Sevillano M. G., Garrido I., and Garrido A. J., Sliding-mode loop voltage control using ASTRA-Matlab integration in tokamak reactors, International Journal of Innovative Computing, Information and Control. (2012) 8, no. 9, 6473–6489.
Web of Science® Google Scholar

Citing Literature

All articles

Asymptotic Hyperstability of a Class of Linear Systems under Impulsive Controls Subject to an Integral Popovian Constraint

Abstract

1. Introduction

2. Problem Statement and Some Preliminary Results

3. Main Results on Asymptotic Hyperstability

4. Some Extensions Concerning Robustness

5. Numerical Examples

5.1. Asymptotic Hyperstability in the Impulsive-Free Case

5.2. Asymptotic Hyperstability in the Presence of Impulses

6. Conclusions

Acknowledgments

Appendices

A. Proof of Lemma 2

B. Proof of Lemma 5

C. Proof of Theorem 9

D. Proof of Theorem 10

E. Outline of Proof of Theorem 13

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley