Abstract and Applied Analysis
Volume 2013, Issue 1 358010
Research Article
Open Access

Multiple Input Delays Estimation Using an Artificial Bee Colony Algorithm

Wei-Der Chang, 

Corresponding Author

Wei-Der Chang

Department of Computer and Communication, Shu-Te University, Kaohsiung 824, Taiwan stu.edu.tw

Search for more papers by this author
First published: 12 September 2013
https://doi.org/10.1155/2013/358010
Academic Editor: Chang-Hua Lien

Abstract

This paper focuses on the time delay estimation of the system described in the form of discrete-time state equation with multiple input delays. To estimate the input delays, a new evolutionary computation called the artificial bee colony (ABC) algorithm is utilized. This algorithm is originally motivated from the social behaviors of honeybee organization, and it has been proven to be a powerful means for solving the optimized problem. Based on the proposed algorithm, the unknown system input delays can be further solved by minimizing a quadratic cost function of the system. Two illustrative examples are provided to verify the potential of the presented method in the time delay estimation. Some simulations containing different initial condition examinations and appearance of noises are further given. Numerical results show that the proposed method can do well in the multiple inputs delay estimation of discrete-time state equations.

1. Introduction

Among numerous evolutionary computations developed in recent years, artificial bee colony (ABC) algorithm has attracted many researchers’ considerable attentions and also been applied in a variety of engineering optimization problems. It was initially developed by Karaboga and spread out by his research teams [1–4], and it is a population-based optimization algorithm like other evolutionary computations. Thus, this algorithm is in parallel to seek for the global or near global solution of the optimized problem, not a single direction search such as the gradient descent method. The ABC algorithm is motivated from the physical bee swarm behavior and possesses a powerful searching capacity on optimizations. In the real honeybee colony, there are three different types of foragers which are the employed bees, onlookers, and scouts [1]. The employed bee is a bee that is going to the food source visited by itself previously, the onlooker is a bee that is waiting on the dance area for making decision to select some food source, and the scout bee means that a bee is carrying out random search for food sources. Furthermore, each employed bee goes to one food source, and, therefore, this implies that the number of employed bees is identical with the number of food sources. An employed bee will become a scout when her food source is exhausted by herself and onlooker bees.

In [1], Karaboga and Basturk have shown that the proposed algorithm is superior to some evolutionary algorithms, for example, genetic algorithm, particle swarm optimization, particle swarm inspired evolutionary algorithm, and so on. A large number of engineering applications combined with the ABC algorithm have been developed in recent years [5–11]. In [5], a nonlinear chemical CSTR process system was controlled by using proportional-integral-derivative (PID) controller from the stable equilibrium point to unstable equilibrium point. The design method for tuning PID control gains is the ABC algorithm. In [7], the authors proposed an optimal design method for the reactive power flow in which the active power loss was minimized by the ABC approach. In machining operations, selection of cutting parameters is an essential task for reducing the cost of products. Yildiz developed an optimization approach by using artificial bee colony algorithm for optimal selection of cutting parameters in multipass turning operations. Simulation results revealed that the ABC algorithm outperforms other optimization techniques [8]. Besides, Huang and Liu presented the ABC algorithm to enhance the fault section estimation performance in power systems [9]. The proposed method can reduce the possibility of inaccurate diagnosis and find the accurate fault section among voluminous alarms.

Another issue considered in this paper is concerned with the time delay estimation. Time delay problem often occurs in many physical situations such as sensor array, sonar, medical imaging, and communications because of the inherent system dynamics and instrumentations. Especially for the control engineering and system identification, the time delay information is of importance. It is attractive and practical to directly estimate these delays according to the measured data rather than making an attempt to obtain them from a physical understanding of systems [12]. To cope with time delay estimation, many techniques were developed in the literature [12–17]. In [14], the authors proposed a novel time delay estimation approach by sliding discrete Fourier transform, and the maximum magnitude of the spectrum and its corresponding phase offset were utilized. It was shown that the proposed method outperforms the standard correlation-based method. Shaltaf then developed a Neurofuzzy-based approach combined with discrete cosine transform (DCT) coefficients for time delay estimation problem [15]. However, a design method for system time delay estimations based on using ABC optimization algorithm seems not to be reported to date. Thus, this paper will focus on the issue of multiple time delays estimation and develop an ABC-based approach to solve such a delay estimation problem. It is requested to define a quadratic cost function of the system at the beginning; the developed ABC algorithm then minimizes this function by means of certain mechanisms, and the actual time delays can be estimated correctly. Besides, the effect of initial condition of the algorithm on the estimation performance is also considered. The rest of this paper is organized as follows. In Section 2, the system formulation for multiple input time delays of discrete-time state equations is addressed. The concept and evolutionary computation of the ABC algorithm is firstly introduced in Section 3, and the design steps combined with ABC for such a time delay estimation is proposed. In Section 4, two illustrative examples are given to confirm the potential of the developed method, and some examinations including different independent runs and appearance of noises are further performed. Finally, Section 5 gives some simple conclusions.

2. System Formulations

In this section, the following system that is expressed by the discrete-time state equation with multiple input delays is considered [16]:
()
where x(k) = [x1(k), x2(k), …, xn(k)] ∈ Rn is the state variable vector of the system at time k, ui(k) ∈ R, for i = 1, 2, …, p, represents the ith system input, A ∈ Rn×n is the coefficient matrix of the system and it is here assumed to be known, Bi ∈ Rn, for i = 1,2, …, p, is also a known coefficient vector, and τ1, τ2, …, τp denote the unknown integer time delays which will be estimated. Moreover, it is assumed that the n system state variables in (1) are observed at each time k. In order to estimate these input delays accurately, the following mathematical model for (1) is given:
()
where is the state variable vector of this estimated model at time k, ui(k) ∈ R is the same as one of (1), represent the estimates of actual input delays τ1, τ2, ⋯, τp, and they should be integer constants as well. The ABC algorithm is utilized such that the estimated values can approximate the actual ones. Before solving the estimation problem, a proper cost function of the system needs to be defined. In this study, a sum of squared error of system states is used over a given time frame as follows
()
where is the error vector of the system between x(k) and and N is the sampling number. It can be seen that better estimation results are obtained by minimizing (3). For simplicity, these estimates of input time delays are collected to form a parameter vector as
()
In the viewpoint of ABC algorithm, the cost function of (3) and the parameter vector of (4) are referred to as the nectar amount and the food source, respectively. Moreover, a food source represents a possible solution of the optimized problem and a large number of food sources then forms the so-called population. From (3), it is clearly seen that the food sources greatly affect the cost function value. Our purpose is to evolve these food sources successively according to some mechanisms of ABC algorithm such that the best food source (i.e., this food source is with the lowest cost function value) is obtained. Next section further introduces the detailed ABC algorithm and its designing steps on time delay estimation.

3. ABC Algorithm and Its Application to Time Delay Estimation

In recent years, Karaboga and his teams have developed a large number of literatures regarding the ABC algorithm and its application to diverse engineering fields such as cluster [3], parameter optimization [18], and symbolic regression [19]. They already showed that the ABC algorithm is an efficient means for solving the optimization problems and is superior to other evolutionary computations like GA, PSO, and DE algorithms. The foragers of honeybee society consist of the following behavior models [1, 5]. Firstly, a set of food source positions are chosen at random by bees, and the nectar amount related to each food source is calculated. These honeybees then come back to the hive to share the nectar information of sources with other bees that are waiting on the dance area. Secondly, each of employed bees, after sharing the information, still goes to the neighborhood of the original food source which was visited by herself previously and then selects a new food source by visual information. Thirdly, the onlooker prefers a food source area depending on the nectar information shared by employed bees on the dance area. While the nectar amount of a food source increases, the probability of choosing such a food source by an onlooker increases as well. The onlooker bee then flies to arrive at the selected area and seeks for a new food source around this area. Visual information is based on the comparison of food source positions. Lastly, a scout bee will randomly find out a new food source to take the place of the previous one when its nectar is abandoned by the honeybee. The artificial bee colony is developed by mimicking such model of foraging bees.

Following the above descriptions, some central components of the ABC algorithm need to be explained in detail [1, 5].

3.1. Food Source

In the ABC algorithm, the notation for the ith food source is denoted by Θi. Each of food sources represents a possible candidate solution to the optimized problem, and note that the number of food sources is the same with that of employed bees. As can be seen from (4), for time delay estimation problem, the ith food source can be further expressed by Θi = [θi1, θi2, …, θip] consisting of p elements.

3.2. Population Size

A population is composed of numerous food sources, and here it is assumed that the size of population is H. Thus, for each food source position, it can be denoted by θij for i = 1, 2, …, H and j = 1, 2, …, p.

3.3. Probability Related to Food Source

In the ABC algorithm, a probability value needs to be evaluated for each of food sources. This probability is concerned with its cost function as defined in (3) and determines whether an onlooker bee chooses a new food source or not. The probability related to the ith food source Θi is defined by
()
where J(Θi) is the cost function evaluated by Θi (the nectar amount of the ith food source). From (5), it can be realized that such a probability value is proportional to the cost function of every food source.

3.4. New Food Source Position

A new food source position can be generated around the present one θij in accordance with the following equation:
()
where is the new position after updating, ϕij ∈ [−2, 2] is a uniformly random number, which greatly dominates the making of a new food source position around θij, and m ∈ {1, 2, …, H} is a random integer constant as well but m ≠ i. Equation (6) represents a comparison of neighbor food positions visually by foraging honeybees, and the ABC algorithm uses (6) to achieve the optimization for a given problem. Moreover, it should be noticed for time delay estimation problem that the estimates of the mathematical model equation (2) are requested to be integer constants; therefore, it is necessary to take the integer part of every food source position to evaluate the mathematical model and the cost function of each food source after executing (6) and for initial positions.

3.5. Abandoned Food Source

In the real-world situation, the food source may be further replaced by a new food source when its nectar has been abandoned by honeybees. In the ABC algorithm, therefore, if the cost function derived from some food source cannot be improved through an assigned number of generations (here called limit), such a food source is abandoned. After that, a new food source instead of the abandoned one will be produced from the original interval.

3.6. Termination Condition

This algorithm stops if the number of generations achieves the maximum allowable number G which is assigned by the designer.

Designing steps for solving the time delay estimation problem based on ABC algorithm can be summarized in the following.

Data. A discrete-time state equation with some unknown input delays described by (1), a mathematical model of (2) for modeling (1), control input ui(k) ∈ R for i = 1,2, …, p, the sampling number N, population size H, parameter limit, and number of generations G.

Goal. Accurately estimate the real input delays τ1, τ2, …, τp of (1) by using the proposed ABC algorithm to minimize the cost function defined in (3).

Step 1. In the beginning, a population consisting of H food sources is randomly established from the interval [0, 1].

Step 2. If an assigned number of generations G is achieved, then the algorithm stops.

Step 3. Calculate the cost function J(Θi) of every food source Θi by using (3).

Step 4. Evaluate every probability Pr(Θi) of Θi by using (5).

Step 5. Generate a random number from [0, 1], and if the probability Pr(Θi) is less than this generated number, then a new food source is derived by means of (6).

Step 6. Further calculate , and let this new food source replace the original Θi if <J(Θi); otherwise, the present food source Θi still remains, and the new one is discarded.

Step 7. When the number of generations is equal to the number, limit, check every Θi whether its positions have been modified or not. If not yet, this food source is removed, and correspondingly a new food source is generated from the initial interval [0, 1].

Step 8. Go back to Step 2.

4. Illustrative Examples

This section will show the applicability of the ABC-based approach to the time delay estimation by using two illustrative examples. For all the following simulations, the related parameter setting for the ABC algorithm is given by the population size H = 40, limit = 20, number of generations G = 100, and sampling number N = 200 in (3).

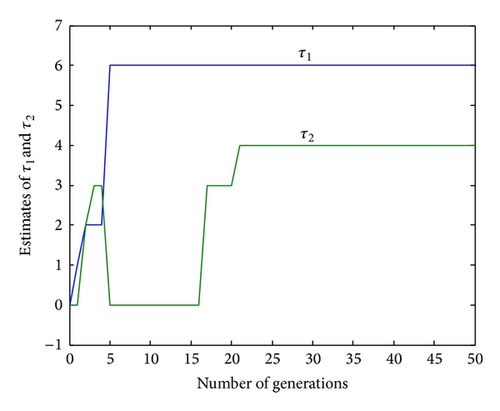
Example 1. Let us consider the first example which is a discrete-time state equation with three state variables and two system inputs described by [16]

()
where τ1 = 6 and τ2 = 4 are the real input time delays and will be estimated. Correspondingly, a mathematical model for (7) is constructed by
()
where and denote the estimates of τ1and τ2, respectively. It is assumed that the initial values are given by x1(0) = 0, x2(0) = 0, and x3(0) = 0 for the system and , , and for the model. In addition, system inputs u1and u2 are two uniformly random numbers generated from the interval [−1, 1]. After executing the proposed ABC algorithm with these data, simulation results are listed in Table 1 and displayed in Figure 1, respectively. In Table 1, it is clearly shown that the estimates and are all exactly the same with τ1 = 6 and τ2 = 4 from ten runs with different initial conditions of the algorithm. Convergence trajectories of τ1 and τ2 with respect to number of generations is shown in Figure 1 only for Run 1. After performing about 25 iterations, the actual time delays can be correctly estimated.

Table 1. Estimation results for Example 1.
 
Run 1 6 4
Run 2 6 4
Run 3 6 4
Run 4 6 4
Run 5 6 4
Run 6 6 4
Run 7 6 4
Run 8 6 4
Run 9 6 4
Run 10 6 4
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Estimates of τ1 and τ2 for Run 1 of Example 1.

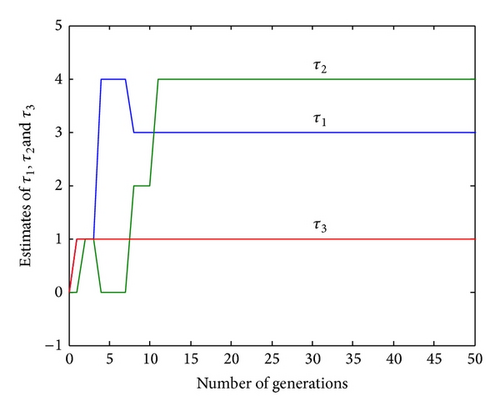
Example 2. In the second example, a discrete-time state equation with two state variables and three system inputs is considered and can be expressed by

()
where three input delays τ1 = 3, τ2 = 4, and τ3 = 1 are given, respectively. As the same as Example 1, three system inputs are all generated from [−1, 1] randomly to excite the responses, and all initial values are assumed to be zero. However, in this case the effect of measurement noises on estimation performance is involved. It is assumed that two Gaussian signals N1(0, 0.1) and N2(0, 0.1) shown in Figure 2 are incorporated into the system states x1 and x2, respectively, as measurement noises. Also, ten different runs are illustrated for examining the robustness of the developed algorithm. Table 2 lists the estimation results for Example 2, and all simulation results from any independent run reveal that the input time delays can be correctly estimated even though measured noises appear. Figure 3 then displays the convergence of time delay estimations for Run 1. As can be seen from the figure, the estimates all approach the actual values after some generations.

Table 2. Estimation results for Example 2.
 
Run 1 3 4 1
Run 2 3 4 1
Run 3 3 4 1
Run 4 3 4 1
Run 5 3 4 1
Run 6 3 4 1
Run 7 3 4 1
Run 8 3 4 1
Run 9 3 4 1
Run 10 3 4 1
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Gaussian noises N1(0, 0.1) and N2(0, 0.1) for Example 2.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Estimates of τ1, τ2, and τ3 for Run 1 of Example 2.

5. Conclusions

This paper has successfully developed an estimation approach for the discrete-time state equation with multiple input time delays. The estimation method is based on the artificial bee colony algorithm which is one of new evolutionary computations. By mimicking the social behaviors of honeybees, such an algorithm can be used to solve the system optimization problem. In this paper, the detailed descriptions for ABC algorithm have been presented, and the design steps combined with the proposed ABC algorithm have also been given for multiple input time delay estimations. It is concluded form two illustrative examples that the ABC-based approach has a satisfactory outcome for solving the time delay estimation problem.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.