Observer-Based Robust H∞ Control for Switched Stochastic Systems with Time-Varying Delay
Abstract
This paper investigates the problem of observer-based robust H∞ control for a class of switched stochastic systems with time-varying delay. Based on the average dwell time method, an exponential stability criterion for switched stochastic delay systems is proposed. Then, H∞ performance analysis and observer-based robust H∞ controller design for the underlying systems are developed. Finally, a numerical example is presented to illustrate the effectiveness of the proposed approach.
1. Introduction
Switched systems are a kind of hybrid dynamical systems composed of a set of continuous-time subsystems or discrete-time subsystems and a switching law that orchestrates the switching between them. Switched systems have attracted increasing attention during the past decades because of their wide applications in real-world systems, such as robot control systems [1], networked control systems [2, 3]. Many useful results on stability analysis and control synthesis for such systems have been reported in [4–8]. For example, H∞ control of switched linear discrete-time systems with polytopic uncertainties was investigated in [8].
It is well known that the time delay phenomenon is frequently encountered in engineering and social systems, and the existence of which may cause instability or undesirable system performance. Therefore, many research efforts have been devoted to the study of switched time delay systems [9–15]. On the other hand, stochastic systems have attracted considerable attention during the past several decades. Early results can be found in [16], and the H∞ control problem of stochastic systems with time delay was investigated in [17, 18]. The study on H2/H∞ control of stochastic system was developed in [19]. Stability analysis on stochastic system with multiple delays was proposed in [20]. Moreover, some results on switched stochastic systems with and without time delay have been obtained (see [21–25] and the references cited therein).
In many real-world systems, state feedback control will fail to guarantee the stabilization because the states of the systems are not all measurable [26]. One of the key approaches to solve the problem is to reconstruct the states of the systems and realize the required feedback control. Hence, the observer-based control has been an interesting topic in control theory. Some results on observer-based control for stochastic delay systems or Markovian jump systems have been presented in [27–29]. However, to the best of our knowledge, the problem of observer-based robust H∞ control for switched stochastic systems with time delay has not been fully studied, which motivates the present study.
In this paper, we aim to design an observer-based robust H∞ controller for switched stochastic systems with time delay such that the closed-loop system is mean-square exponentially stable with H∞ performance. The major contributions of the work can be summarized as follows: (1) a new Lyapunov-Krasovskii functional candidate is introduced to derive the exponential stability of switched stochastic systems with time delay, and the free-weighting matrix method is employed to reduce the conservatism; (2) an observer-based robust H∞ controller design scheme for the underlying systems is proposed.
The remainder of the paper is organized as follows. In Section 2, problem statement and some useful lemmas are given. In Section 3, the main results are presented. In Section 4, a numerical example is given to illustrate the effectiveness of the proposed approach. Finally, concluding remarks are provided in Section 5.
Notation. In this paper, the superscript “T” denotes the transpose, and the symmetric term in a matrix is denoted by ∗. The notation X > Y (X ≥ Y) means that X − Y is positive definite (positive semidefinite, respectively). Rn denotes the n-dimensional Euclidean space. ∥x(t)∥ denotes the Euclidean norm. |a| denotes the absolute value of a. L2[t0, ∞) is the space of square integrable functions on [t0, ∞), and t0 is the initial time. λmax (P) and λmin (P) denote the maximum and minimum eigenvalues of P, respectively. A+ denotes the Moore-Penrose pseudoinverse of A. I is the identity matrix. diag {ai} denotes a diagonal matrix with the diagonal elements ai, i = 1,2, …, n.
2. Problem Formulation and Preliminaries
Remark 1. It is noted that the observer-based H∞ control for stochastic systems or Markovian jump systems was considered in [27–29]. However, the results in the aforementioned papers cannot be directly applied to the switched stochastic system considered in the paper. This motivates our study. Also, the proposed observer in (6a), (6b), and (6c) is a switching observer, which is different from the existing ones given in [27–29].
Assumption 2. Bi is full row rank, for all .
Definition 3. System (1a), (1b), (1c), and (1d) with v(t) = 0 is said to be mean-square exponentially stable under the switching signal σ(t) if there exist scalars κ > 0 and α > 0, such that the solution x(t) of the system satisfies
Definition 4 (see [24].)For any T2 > T1 ≥ t0, let Nσ(T1, T2) denote the switching number of σ(t) on an interval [T1, T2). If
Definition 5 (see [30].)For any λ > 0 and γ > 0, system (7a), (7b), and (7c) is said to be mean-square exponentially stable with a prescribed weighted H∞ performance level γ if the following conditions are satisfied:
Lemma 6 (see [31].)For any positive symmetric constant matrix M ∈ Rn×n and a scalar r > 0, if there exists a vector functiong : [0, r] → Rn such that integrations in the following are well defined, then the following inequality holds
Lemma 7 (see [32].)Let U, V, W, and X be constant matrices of appropriate dimensions with X satisfying X = XT, then for all VTV ≤ I, X + UVW + WTVTUT < 0 if and only if there exists a scalar ε > 0 such that X + εUUT + ε−1WTW < 0.
The objective of this paper is to design an observer-based robust H∞ controller for switched stochastic delay system (1a), (1b), (1c), and (1d) such that the augmented closed-loop system (7a), (7b), and (7c) is mean-square exponentially stable with a prescribed weighted H∞ performance level γ.
3. Main Results
3.1. Stability Analysis
Theorem 8. For a given scalar α > 0, if there exist symmetric positive definite matrices Pi, Qi, and Ri and any matrices Si such that
Proof. Let Y(t) = Aσ(t)x(t) + Aτσ(t)x(t − τ(t)), then (13a) can be described as
Choose the following Lyapunov functional candidate for the ith subsystem
For the sake of simplicity, Vi(t, x(t)) is written as Vi(t) in this paper. According to Itô’s formula, along the trajectory of the ith subsystem, we have
According to Lemma 6, we have
Integrating both sides of (18) from t − τ(t) to t, we have
Thus,
By using the Schur complement, we obtain from (14) that
According to (26), one obtains that
Then, taking mathematical expectation, we have
From (16) and (19), we obtain that
Let σ(tk) = i. Then, using formula, we can obtain that for t ∈ [tk, tk+1),
Notice that
Thus, it can be obtained that
Noticing that E{V(t)} ≤ sup −τ≤θ≤0 E{V(t + θ)}, one gets
For any t ∈ [tk, tk+1), from (16) and (36), it follows that
When (15) holds, noticing that Nσ(t0, t)≤(t − t0)/Tα, one has
The proof is completed.
Remark 9. In the derivation of Theorem 8, a new Lyapunov-Krasovskii functional candidate is constructed for the stability analysis of switched stochastic systems with time delay, and it is different from the ones given in [9–15]. Also, the free-weighting matrix method is utilized to reduce the conservatism.
Remark 10. If μ = 1 in (15), which leads to Pi = Pj, Qi = Qj, and Ri = Rj, for all , then system (13a) and (13b) possesses a common Lyapunov function, and the switching signals can be arbitrary.
From Theorem 8, we can readily get the exponential stability criterion for switched system (39a) and (39b).
3.2. H∞ Performance Analysis
Theorem 12. For a given scalar α > 0, if there exist symmetric positive definite matrices Pi, Qi, and Ri and any matrices Si such that
Proof. We can easily obtain that (14) is satisfied if (42) holds. Thus, system (41a), (41b), and (41c) with v(t) = 0 is mean-square exponentially stable.
When v(t) ≠ 0, let
Choosing the same Lyapunov functional candidate as (19) and following the proof line of Theorem 8, we have
Using the Schur complement, from (42), we get
It follows that
From (44), we obtain that
For any t ∈ [tk, tk+1), using formula and taking the mathematical expectation, one has
Under the zero initial condition, we obtain that
According to (46), one has
Multiplying both sides of (55) by leads to
Noticing that Nσ(t0, s)≤(s − t0)/Tα and Tα ≥ τ + ln (χμ)/λ ≥ ln μ/λ, one obtains that
When t → ∞, the following inequality is derived:
The proof is completed.
3.3. Observer-Based Robust H∞ Stabilization
Now, we are in a position to design an observer-based robust H∞ controller for system (1a), (1b), (1c), and (1d) such that the augmented closed-loop system (7a), (7b), and (7c) is mean-square exponentially stable with a prescribed weighted H∞ performance level γ. Based on Theorem 12, a sufficient condition for the existence of such a controller is presented in the following theorem.
Theorem 13. Consider system (1a), (1b), (1c), and (1d), for a given scalar α > 0, if there exist scalars εi > 0, symmetric positive definite matrices Pi, Qi, and Ri, and any matrices , Yi, and Zi such that, for all ,
Moreover, if the above conditions have a feasible solution, the controller gain matrices and the observer gain matrices can be obtained by and .
Proof. According to Theorem 12, we get that system (7a), (7b), and (7c) is mean-square exponentially stable with a weighted H∞ performance level γ if the following inequality is satisfied:
Then, we have
From Lemma 7, we have
Thus, according to Theorem 12, we obtain from (59)–(62) that system (7a), (7b), and (7c) is mean-square exponentially stable with a weighted H∞ performance level γ. Moreover, we can obtain the controller gain matrices and the observer gain matrices .
The proof is completed.
Remark 14. An observer-based H∞ controller design scheme is proposed in the paper. Compared with the existing results presented in [27–29], a remark advantage of the work is that the proposed observer is mode-dependent, which means that each subsystem has its individual observer. Moreover, the proposed observer not only ensures the convergence of the estimated error of each subsystem, but also guarantees that the estimated error of the whole system converges to zero exponentially.
In Theorem 13, when we choose that Qi = Ri = Pi, it is not difficult to get that βi = 1 and χ = χi = 1 + τ(1 + τ)(eλτ − 1), for all . Then, the following corollary is derived.
Corollary 15. Consider system (1a), (1b), (1c), and (1d), for a given scalar α > 0, if there exist scalars εi > 0, symmetric positive definite matrices Pi > 0, and matrices , Yi, and Zi such that, for all ,
Moreover, the controller gain matrices are , and the observer gain matrices are .
4. Numerical Example
Moreover, we have μ = 4.3051, λ = 0.7, χ = 1.3143, and . Taking , and letting , t ∈ [−0.5,0), , and , and simulation results are shown in Figures 1–5.
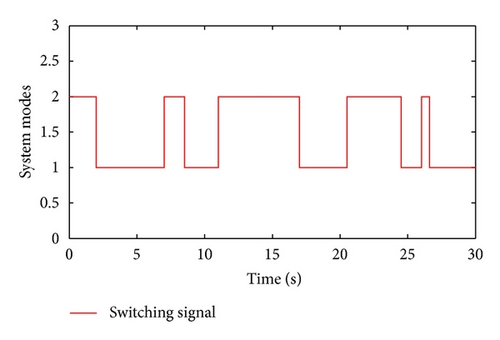
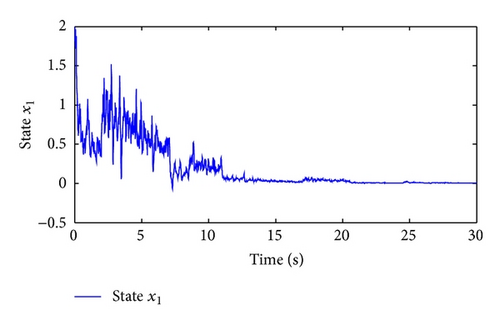
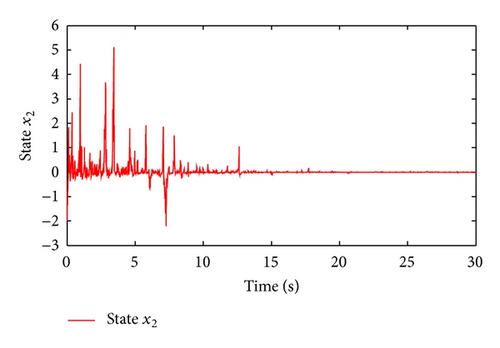
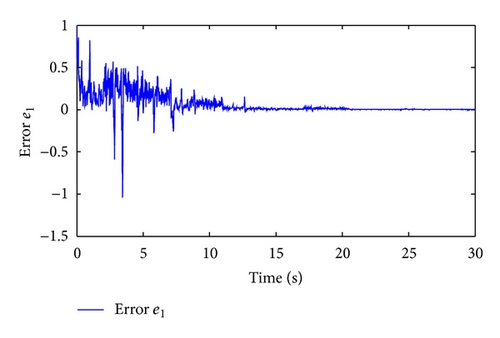
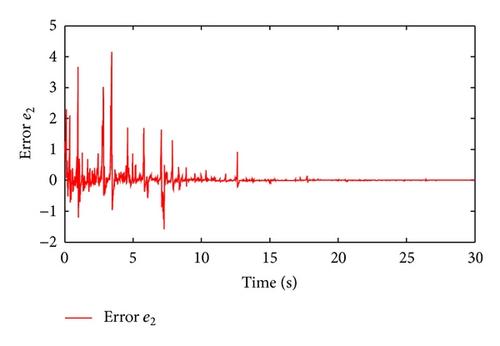
Figure 1 shows the switching signal of the switched system with the average dwell time Tα = 3. Figures 2 and 3 illustrate the state trajectories of the closed-loop system. The estimated errors are plotted in Figures 4 and 5, respectively. We can see from Figures 2–5 that the proposed observer can guarantee the convergence of the estimated error and the designed controller can guarantee the stability of the corresponding closed-loop system. This demonstrates the effectiveness of the proposed method.
In addition, some observer-based controller design approaches proposed in the existing literature [27–29] are only applicable to stochastic systems or Markovian jump systems and they cannot be used to stabilize the system considered in this section, which also shows the advantage of the proposed method.
5. Conclusions
In this paper, the problem of observer-based robust H∞ stabilization for stochastic switched systems with time delay has been investigated. By using the average dwell time method, sufficient conditions which guarantee the mean-square exponential stability of switched stochastic systems with time delay are derived. Then, H∞ performance analysis and observer-based H∞ control for such systems are developed. Finally, a numerical example is given to demonstrate the effectiveness of the proposed approach.
Acknowledgment
This work was supported by the National Natural Science Foundation of China under Grant No. 61273120.




