A New Legendre Spectral Galerkin and Pseudo-Spectral Approximations for Fractional Initial Value Problems
Abstract
We extend the application of the Galerkin method for treating the multiterm fractional differential equations (FDEs) subject to initial conditions. A new shifted Legendre-Galerkin basis is constructed which satisfies exactly the homogeneous initial conditions by expanding the unknown variable using a new polynomial basis of functions which is built upon the shifted Legendre polynomials. A new spectral collocation approximation based on the Gauss-Lobatto quadrature nodes of shifted Legendre polynomials is investigated for solving the nonlinear multiterm FDEs. The main advantage of this approximation is that the solution is expanding by a truncated series of Legendre-Galerkin basis functions. Illustrative examples are presented to ensure the high accuracy and effectiveness of the proposed algorithms are discussed.
1. Introduction
Many practical problems arising in engineering, physical, biological, and biomedical sciences require solving fractional differential equations (FDEs), (see, e.g., [1–4]). For that reason, accurate and efficient numerical approaches for solving FDEs are needed. Several methods have also been proposed in the literature to solve ordinary or partial fractional differential equations (see, for instance, [5–8]). In contrast, there is a relatively small literature on spectral methods for direct solution of such fractional-order problems, (see, for instance, [9–11]).
The aim of this paper is to design some spectral techniques based on the shifted Legendre-Galerkin (SLG) method and shifted Legendre-Gauss-Lobatto collocation (SL-G-LC) method in modal basis for the solution of linear and nonlinear multi-term FDEs, respectively. Indeed, this is the first work concerning the spectral Galerkin method and pseudo-spectral method in modal basis for solving such problems.
In the tau, Galerkin, or pseudo-spectral approximations, the spectral solution is represented by a truncated series of smooth global trial functions, in such a representation the coefficients of the expansion are the unknown to be determined. An explicit expression for the derivatives of an infinitely differentiable function of any degree and for any fractional order in terms of the function itself is needed for tackling FDEs. In this direction, Doha et al. [9] have derived such a formula in the case of the trial functions of truncated expansion that are Chebyshev polynomials and implemented such a relation for solving two classes of FDEs. Furthermore, the fractional derivative of shifted Jacobi polynomials is derived in [12]. Ahmadian et al. [13] proposed an accurate and reliable computational scheme based Jacobi polynomials for fuzzy linear FDEs.
The pseudo-spectral methods for the numerical approximations of the solution of several types of FDEs have been proposed and developed. Maleki et al. [14] proposed an efficient and accurate pseudo-spectral method based on shifted Legendre-Gauss quadrature nodes for solving a class of FDEs with boundary conditions. The authors of [15] used the spline functions methods for tackling the linear and nonlinear FDEs. The authors of [16] proposed two types of spectral approximations based on shifted Legendre polynomials for solving two classes of FDEs with multipoint boundary conditions. Yüzbaşı [17] proposed the Bessel pseudo-spectral method to introduce an approximate solution of a class of FDEs. A collocation method based on Bernstein polynomials has recently been proposed and analyzed for solving fractional order Riccati differential equation in [18]. Moreover, the authors in [11] computed the fractional derivative of the new fractional Legendre functions (FLF), also they developed an efficient spectral tau approximations based on FLF to approximate the FDEs. Recently, Bhrawy et al. [19] investigated the fractional integrals of modified generalized Laguerre operational matrix to implement a numerical solution of the integrated form of the linear FDEs on semi-infinite interval. Meanwhile, Baleanu et al. [20] proposed and developed two efficient generalized Laguerre spectral algorithms based on the operational matrix of derivative for the solution of linear and nonlinear fractional initial value problems. We refer also to the recent papers [21–27] where several numerical methods are developed to approximate the solution of various kinds of FDEs.
The fundamental goal of this paper is to develop a direct solution technique to approximate linear FDEs subject to homogeneous initial conditions, using the shifted Legendre spectral Galerkin (SLG) approximations. We start by constructing a new appropriate shifted Legendre basis functions which satisfy the homogeneous initial equations and then are used for the approximation of the fractional differential operators. We also present an explicit expression for the derivatives of any fractional order for the shifted Legendre basis functions in terms of the shifted Legendre polynomials. Moreover, the matrices corresponding to shifted Legendre-Galerkin approximation are clearly described, including the modes required to impose nonhomogeneous initial conditions.
Another goal of this paper is to treat the nonlinear FDEs subject to nonhomogeneous initial conditions by implementing a new pseudo-spectral approximation based on Legendre polynomials. This approach is characterized by the representation of the solution by a truncated series of Legendre-Galerkin basis functions. The proposed technique differs from the classical pseudo-spectral approximation in that the homogeneous initial conditions are satisfied exactly. Finally, the accuracy and effectiveness of the proposed algorithms are demonstrated by some numerical examples.
The outline of the paper is as follows. Section 2 introduces necessary definitions of fractional derivatives and shifted Legendre polynomials. In Section 3, we construct an appropriate shifted Legendre basis function for initial FDEs and prove a formula that gives the fractional derivatives of the shifted Legendre basis function in terms of the shifted Legendre polynomials. In Section 4, we present and develop the Legendre-Gauss-Lobatto collocation algorithm in modal basis for solving nonlinear FDEs. In Section 5, some numerical results are discussed. Section 6 is devoted to concluding remarks.
2. Preliminaries and Notations
We present recall and in this section recall some properties of the fractional calculus (see, e.g., [1–4]) and Legendre polynomials.
In the following theorem, we state the Caputo fractional derivative of order μ for the shifted Legendre polynomials, for more details, see [16].
Theorem 1 (see [16].)The Caputo fractional derivative of order μ of the shifted Legendre polynomials is given by
3. Legendre-Galerkin Method for Fractional IVPs
The problem of approximating solutions of multi-term fractional differential equations by shifted Legendre-Galerkin approximation involves the projection onto the span of some appropriate sets of shifted Legendre basis function. The members of the basis may satisfy automatically the given initial conditions imposed on the multi-term FDEs (11). The following lemma provides a shifted Legendre basis function which satisfies the homogeneous initial conditions (12).
Lemma 2. Let one defines
Proof. As a general rule, for fractional-order differential equations with m initial conditions, one may choose the basis function ϕk(x), in the form (see, [28, 29])
Remark 3. The computation of the exact solution of the linear system (19) for the unknown coefficients {ηi,m(k)} is extremely tedious by hand and we have resorted to the symbolic computation software Mathematica 8.
In the following theorem, we introduce a formula expanding explicitly the fractional derivatives of the basis functions for any fractional-order in terms of shifted Legendre polynomials.
Theorem 4. The Caputo fractional derivative for the shifted Legendre basis functions is given by
Proof. The proofs of the this theorem can be immediately obtained on similar lines to that of Theorem 1 and Lemma 2.
Let us denote that
Theorem 5. If one takes ϕk(x) as defined in (21), and if one denotes , , and , then
Proof. The basis functions ϕk(x) are chosen such that ϕk(x) ∈ VN for k = 0,1, …, N − m, and the dimension of VN is equal to N − m + 1. Hence,
To obtain the elements akj for 0 ≤ k, j ≤ N − m, we set μ = ν in Theorem 4 to get, for j ≥ ⌈ν⌉,
Now, we will transform FDEs with nonhomogeneous initial conditions to other ones with homogeneous initial conditions. Consider the multi-term fractional differential equation (11) subject to the nonhomogeneous initial conditions
The transformation (38) turns the nonhomogeneous initial conditions (37) into the conditions
If we employ the shifted Legendre-Galerkin approximation to the modified problem (41), based on the basis function ϕk(x) which given in (21), we obtain the following system of linear algebraic equations:
4. Shifted Legendre Pseudospectral Approximation in Modal Basis
The main advantage of pseudo-spectral approximation in solving differential equations [30, 31] lies in its high accuracy for a given number of unknowns. In the proposed shifted Legendre-Gauss-Lobatto collocation method in modal basis, there are two successive steps for obtaining the approximate solution of nonlinear fractional initial value problem. First, an appropriate finite set of shifted Legendre basis functions must be chosen for the representation of the truncated solution, and then the nonlinear FDE may be collocated by the well known shifted Legendre-Gauss-Lobatto quadrature nodes. Consequently, The nonlinear FDE is reduced to a system of algebraic equations. In the second step, we implement any standard numerical solver for solving such system of nonlinear algebraic equations.
5. Numerical Examples
In this section, we implement several numerical examples to demonstrate the accuracy and applicability of the proposed spectral algorithms. Comparison of the results obtained by our methods with shifted Jacobi pseudo-spectral approximation [12] reveals that the present algorithms are very convenient and produces high accurate solutions to multi-term FDEs.
Example 1. Consider the linear FDE equation with homogeneous initial conditions
Table 1 lists the maximum absolute error, using the shifted Legendre-Galerkin (SLG) method with various choices of ν and N.
| N − 6 | ν | SLG method | ν | SLG method | ν | SLG method |
|---|---|---|---|---|---|---|
| 8 | 5.1 | 1.00 × 10−3 | 5.5 | 2.30 × 10−3 | 5.9 | 2.88 × 10−3 |
| 16 | 1.19 × 10−7 | 1.11 × 10−6 | 1.47 × 10−6 | |||
| 24 | 7.15 × 10−10 | 1.08 × 10−8 | 1.86 × 10−8 |
Example 2. Consider the linear FDE equation
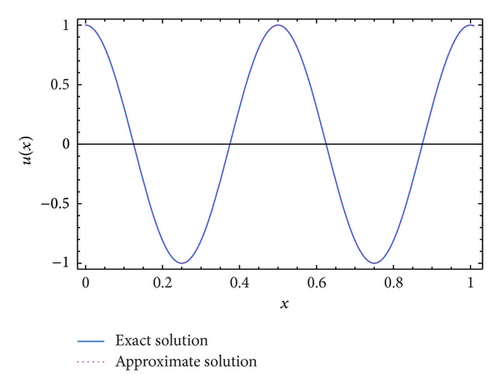
Table 2 lists the maximum absolute error, using the SLG method with various choices of γ and N. Moreover, the approximate solution obtained by the SLG method at γ = 4π and N = 16 is shown in Figure 1 to make it easier to compare with the analytic solution.
| N − 2 | ν | SLG method | ν | SLG method | ν | SLG method |
|---|---|---|---|---|---|---|
| 16 | 1 | 2.87 × 10−4 | π | 3.21 × 10−3 | 2π | 3.99 × 10−1 |
| 20 | 2.47 × 10−5 | 2.43 × 10−4 | 9.96 × 10−4 | |||
| 24 | 6.05 × 10−6 | 6.01 × 10−5 | 2.55 × 10−4 |
Example 3. Consider the nonlinear fractional initial value problem [12]
In Table 3, we introduce maximum absolute error, using SL-G-LC method for ζ = 2.5, η = 1.5, θ = 0.9 with various choices of N.
| N | SL-G-LC | SJ-GC (α = β = 0) | SL-GLC (α = β = 1/2) | SL-GLC (α = β = 1) |
|---|---|---|---|---|
| 4 | 4.06 × 10−4 | 3.91 × 10−3 | 2.73 × 10−3 | 1.84 × 10−3 |
| 8 | 1.61 × 10−4 | 1.42 × 10−3 | 8.66 × 10−4 | 5.40 × 10−4 |
| 16 | 7.06 × 10−5 | 1.24 × 10−4 | 1.17 × 10−4 | 1.03 × 10−4 |
| 24 | 2.33 × 10−5 | 3.37 × 10−5 | 3.50 × 10−5 | 3.39 × 10−5 |
This problem was solved in [12] using shifted Jacobi-Gauss collocation (SJ-GC) method based on Jacobi operational matrix, the results provided by Doha et al. [12] have been presented in the third, fourth, and fifth columns of Table 3 for Jacobi parameters α = β = 0, α = β = 1/2, and α = β = 1, respectively. Numerical results of this FDE demonstrate that the SL-G-LC method is more accurate than the SJ-GC method, see Table 5.7 in [12].
Example 4. Consider the nonlinear fractional initial value problem
In Table 4, we introduce the maximum absolute error, using the shifted Legendre collocation method based on Gauss-Lobatto points, with various choices of ζ, m and N at p = 4.
| N − m | m | ζ | SL-G-LC | ζ | SL-G-LC |
|---|---|---|---|---|---|
| 4 | 3 | 2.5 | 9.29 × 10−3 | 2.9 | 4.80 × 10−3 |
| 8 | 3.29 × 10−3 | 2.44 × 10−3 | |||
| 16 | 1.34 × 10−3 | 2.65 × 10−4 | |||
| 24 | 4.89 × 10−4 | 2.63 × 10−4 | |||
| 4 | 5 | 4.2 | 1.16 × 10−2 | 4.8 | 1.98 × 10−2 |
| 8 | 3.69 × 10−3 | 4.31 × 10−3 | |||
| 16 | 1.47 × 10−4 | 1.89 × 10−3 | |||
| 24 | 1.19 × 10−4 | 7.90 × 10−4 | |||
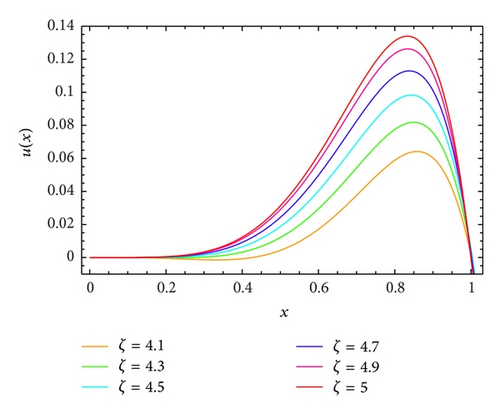
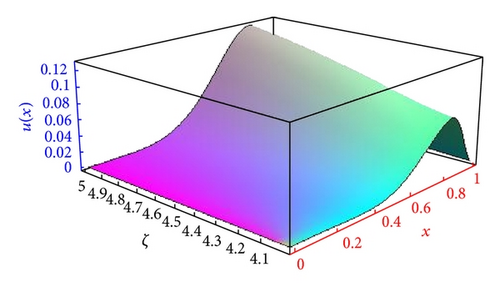
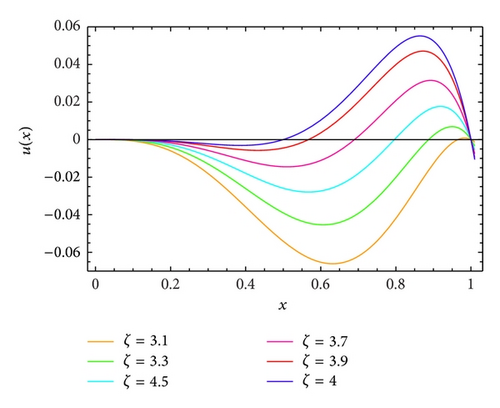
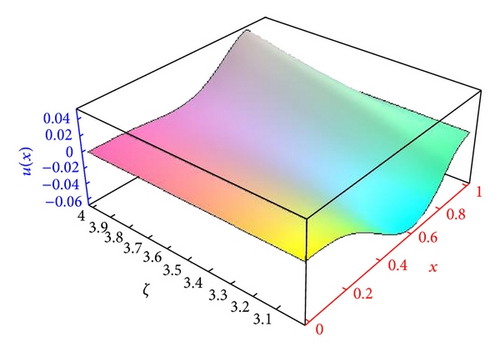
The approximated solutions are evaluated for ζ = 4.1,4.3,4.5,4.7,4.9,5 with m = 5 and p = 2 and 12 nodes. The results of the numerical simulations are plotted in Figure 2. It is evident from Figure 2 that, as ζ approaches close to 5, the numerical solution by shifted Legendre-Gauss-Lobatto collocation method for such FDE approaches to the solution of integer order differential equation. In the case of 4 < ζ ≤ 5, p = 2 with m = 5, and 12 nodes, the results of the numerical simulations are shown in Figure 3. In Figure 4, we plotted the approximated solutions for different choices of ζ, m = 4, p = 3, and 12 nodes. Moreover, the approximate solutions obtained by the present method at 3 < ζ ≤ 4, p = 3 with m = 4, and 12 nodes are shown in Figure 5 to make it easier to show that; as ζ approaches to its integer value, the solution of FDE approaches to the solution of integer order differential equation.
6. Conclusion
We have extended the application of the shifted Legendre spectral Galerkin approximation for treating fractional initial value problems. In this approximation, the initial conditions are satisfied exactly for each member of shifted Legendre basis functions. In particular, any fractional-order Caputo derivative of such basis functions is expanded in terms of the shifted Legendre polynomials. In addition, we have proposed an accurate direct solvers for the general multi-term FDEs with nonhomogeneous initial conditions using the Legendre spectral Galerkin approximation.
In this paper, we proposed a Legendre-Gauss-Lobatto collocation algorithm in model basis for solving the nonlinear FDEs in which the numerical solution was approximated directly using the shifted Legendre basis functions. The results from numerical examples demonstrate the accuracy and stability of these spectral approximations for treating linear and nonlinear FDEs. In the forthcoming works, we hope that similar techniques can be applied to Chebyshev polynomials or other Jacobi polynomials.




