Abstract and Applied Analysis
Volume 2013, Issue 1 281675
Research Article
Open Access

SPICE Mutator Model for Transforming Memristor into Meminductor

Hui Wang, 

Hui Wang

College of Mathematics Science, Chongqing Normal University, Chongqing 401331, China cqnu.edu.cn

Search for more papers by this author
Xin Wang, 

Xin Wang

College of Computer Science, Chongqing University, Chongqing 400044, China cqnu.edu.cn

Search for more papers by this author
Chuandong Li, 

Corresponding Author

Chuandong Li

College of Computer Science, Chongqing University, Chongqing 400044, China cqnu.edu.cn

Search for more papers by this author
Ling Chen, 

Ling Chen

College of Computer Science, Chongqing University, Chongqing 400044, China cqnu.edu.cn

Search for more papers by this author
First published: 31 January 2013
https://doi.org/10.1155/2013/281675
Citations: 5
Academic Editor: Xiaodi Li

Abstract

The memristor (resistor with memory), as the fourth fundamental circuit element, is a nonvolatile nanoelectronic device and holds great promise for VLSI applications. It was suggested that the meminductor (ML, inductor with memory) circuit can be built by memristor emulators. This paper further addresses the transformation mechanism in terms of constitutive relation from the memristor to the meminductor and then designs an MR-ML mutator to achieve MR-ML transformation. We also present the mutator’s SPICE model and analyze the simulation results.

1. Introduction

The memristor (a contraction for memory resistor) was believed to be the fourth fundamental two-terminal passive element, besides the resistor, the capacitor, and the inductor. The element was firstly postulated by Chua [1] to characterize the relationship between the charge and the flux linkage for the sake of the completeness of the circuit theory. However, this pioneer work had not attracted the researchers’ attention until 2008. Strukov et al., at Hewlett Packard, announced the first experimental design of memristor—two TiO2 layers sandwiched between two platinum electrodes [2]. This work has been causing a tremendously increased interest in the field of the theory and applications of the memristor. Progressive potential applications of memristor cover many important areas, such as digital memory logic, analog circuits, and neural synapse [1, 3–7].

The memristor is a special case of a more general memristive system which was defined by Chua and Kang [8]. In 2009, the memcapacitatative and meminductive systems were also formulated in the spirit of memristive systems. As the special types of the memcapacitive and meminductive systems, memcapacitor and meminductor [9] also attract interest of the scientists. Combining with memristive systems, these elements will open up much new and unexpected functionality in the field of electronics [10].

Recently, several emulator models for meminductor and memcapacitor were built [11, 12]. However, these emulator models are complicated for circuit implementation. To conquer this problem, we present a design method of mutator for MR-ML transformation, which makes the circuit realization and theoretical analysis much more convenient and effective. This method can apply easily to build the mutator for MR-MC transformation. In the next section, we will analyze the constitutive relation of meminductor via CR transforming method. Then, the idea for transforming MR to ML is proposed in Section 3. Based on the SPICE model of the memristor, the mutator model for meminductor will be designed in Section 4, and then simulation and analysis results are demonstrated in Section 5. Finally, the conclusions are drawn in Section 6.

2. Constitutive Relation of Meminductor

As discussed in [13], a network element can be defined axiomatically by its constitutive relation, which does not depend on the element interaction with the surrounding networks. The constitutive relation of meminductor is
()
where ρ, q are defined by
()
Assuming that constitutive relation (1) can be depicted as a single-valued function h of charge, namely,
()
where h is a nonlinear function, then the current-controlled meminductor’s constitutive relation can be rewritten as
()
where LM(q) = dh(q)/dq | Q is the small-signal meminductance defined at the operating Q.

3. Transformation from Memristor to Meminductor

In this paper, we use the memristor model proposed in [14] to demonstrate the theoretical possibility of transforming the memristor into the meminductor.

The memristor models presented in [2, 3, 14] are shown in Figure 1. The total resistance of the memristor, RMEM, is a sum of the resistance of the doped and undoped regions, namely,
()
where w and D are the width of the doped region and the total length of the TiO2 layer, respectively, and RON and ROFF are the limit values of the memristor resistance for w = D and w = 0.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The variable resistor model.
The corresponding port equation (PE) of the memristor is
()
where w(t) is the state variable about the length of the doped region in the thin film. dw(t)/dt is proportional to the current passing through the memristor. The model presented in [12] used the window function which is the Joglekar function (f(x) = 1 − (2x − 1) 2p) to model nonlinear dopant drift. But in order to analyze conveniently, we define the window function as f(x) = 1, while choosing the Joglekar function [14] with the parameter p = 1 in model design.
The speed of the movement of the boundary between the doped and undoped regions depends on the resistance of the doped area, on the passing current, and on the other factors according to the states equation [1, 14],
()
Therefore w is a function of charge
()
Based on (8) and 0 ≤ w(t) ≤ D, the condition for the memristor regime is 0 ≤ q(t) ≤ D2/uvRON. Substituting (8) into (5), one can observe that the memristor is acting like a variable resistor with the resistivity M(q) which is a function with respect to charge, namely,
()
From the definition of the memristor dϕ = M(q)dq, it follows that
()
As we know, the constitutive relation of the memristor has the same form with (10). Arguing similarly with [15, 16], we now transform the port equation into the constitutive relation. For this purpose, we denote
()
It follows from (2) that
()
Therefore,
()
By the discussion above, one can see that the meminductance is a function of charge if q ≠ 0, and otherwise h(q) = 0.

Hence, we have obtained the constitutive relation of meminductor ρ(q) (12) and the meminductance (13) LM(q) upon expanding the constitutive relation of the memristor.

4. Mutator from MR into ML

4.1. Characterization of the MR-ML Mutator

The mutator is an active, two-port linear network for transforming one type of nonlinear element into another type. There are three types of mutators—an L-R mutator, a C-R mutator, and an L-C mutator—which have been realized [17]. In this subsection, we introduce an MR-ML mutator which is firstly proposed in [15, 18]. It is characterized by the property that if a nonlinear memristor with a v–i curve γ is connected across port 2 of this element, the resulting one port (seen across port 1) becomes a nonlinear inductor in the sense that it can be characterized by a ϕ-i curve which is identical to the original v-i curve γ. The basic principle of a mutator is as shown in Figure 2.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Characterization of MR-ML mutator.
Inspired by the idea presented in [15], we design a mutator for simulating meminductor through the memristors. The constitutive relations of MR and ML can be accomplished by the following linear transformation of the coordinates φ = kxρML, q = kyqML, where kx and ky are real constants. Their values depend on the way the concrete mutator is implemented. The time-domain differentiation of the linear transformation yields the following: v2 = kx(d/dt)v1, i2 = kyi1. These equations are written in the operator form by means of the transmission matrix T [15]. So we can have the following matrix as the transmission matrix:
()

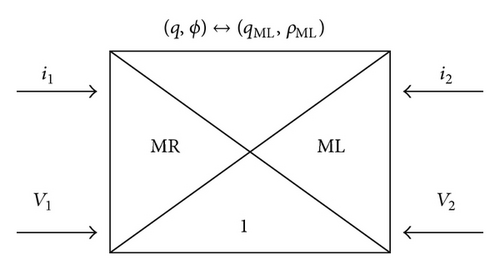
4.2. Demonstration by Example

In this subsection, we apply a sinusoidal current source defined by
()
across this memristor, where A = 1 and ω = 1. One can calculate the corresponding charge (assuming the initial charge q0 = q(0) = 0)
()
Substituting (16) into (10) yields the corresponding flux
()
Substituting (17) into (12) then yields the corresponding TIF (integral of magnetic flux)
()
In a period [−T/2, T/2], it follows from (16) that
()
This together with (18) implies that
()
Note that the constitutive relation holds the following condition which is one of the fingerprints of the meminductors: ρ(q) = 0, for q = 0.
For the existence of higher-order derivative of ρ(q), one can rewrite (20) in the form of the Taylor series [11]:
()
And therefore the meminductance LM(q) is rewritten as
()
or, in form of the Taylor series,
()
From (23) one observes that if γk = 0, for k > 1, the meminductance is independent of the circuit variables; namely, the meminductor behaves as a linear inductor. In other words, the memory effect is described by the remaining terms of the Taylor series just for k > 1. From the constitutive relation ρ(q) of meminductor, (15), and the meminductance LM(q), (13), one observes that the proposed results for meminductor by expanding the constitutive relation of the memristor are well consistent with those in [15].

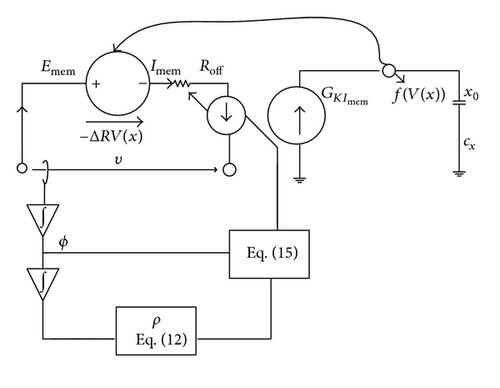
4.3. Realization of MR-ML Mutator Model

In this subsection, we present a mutator to transform MR to ML inspired by the idea in [15, 18, 19]. The PSpice model of the mutator is based on the following steps.
  • (i)

    The terminal voltage of mutator is sensed and led to a cascade of two time-domain integrations in order to get the flux(ϕ) and the TIF(ρ).

  • (ii)

    Based on the knowledge of the charge and TIF, the meminductance is computed from (13).

  • (iii)

    Based on the knowledge of the LM(q) and ϕ, the current i of the meminductor mutator can be computed as follows:

    ()

The PSpice model of the mutator proposed in this paper is shown in Figure 3.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
SPICE model of the mutator.

5. Simulation Results

To verify the effectiveness of the proposed mutator, SPICE simulation is designed and simulation results with series waveforms demonstrate its performance. The run time is set as 2 s. We connect the sinusoidal current source as the excitation of the circuit. The voltage and the current flow through the memristor as the excitation of e port 1.

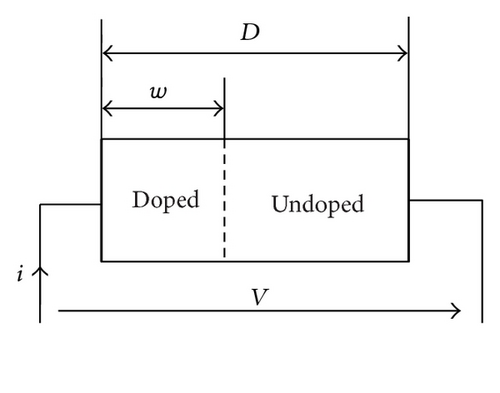
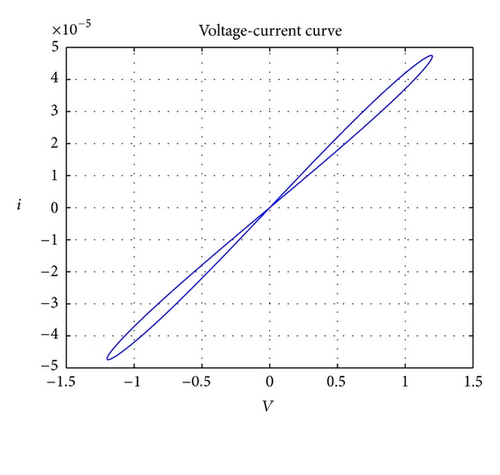
Consider the memristor model shown in Figure 1 with the parameters RON  = 100, ROFF = 16 K, Rinit = 11 k, D ≈ 10 nm, and uv ≈ 10−14 m2 s−1 V−1. As used in [12], the window function is chosen as a smoother Joglekar function with the parameter p = 1. We use the sinusoidal voltage source, with the parameter of the peak amplitude Va = 1.4 V, and the frequency freq = 0.325 HZ. The V-I characteristic of memristor is presented in Figure 4.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
The V-I characteristics of memristor.

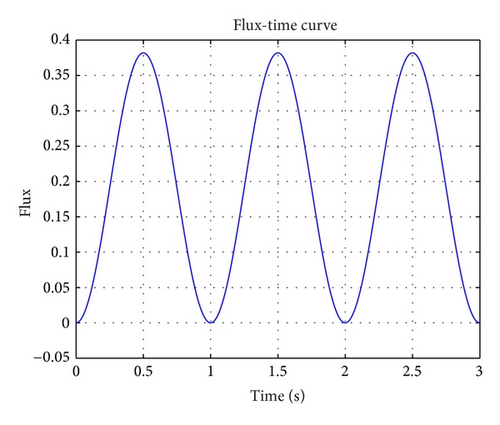
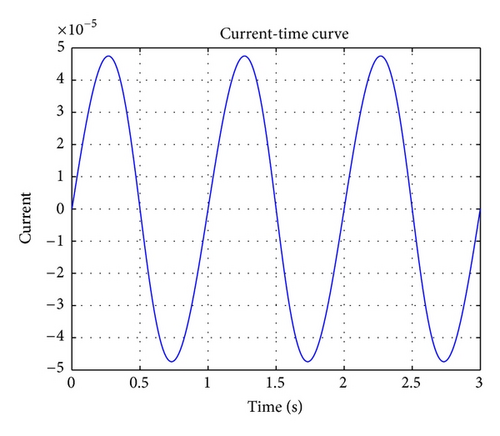
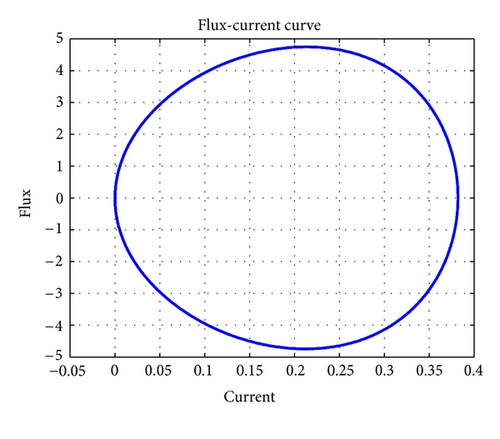
The ϕ(t) curve and the i(t) curve of port 1, which are used to characterize the property of the meminductor, are shown in Figures 5(a) and 5(b). Figure 5(a) represents the flux of the meminductor, and Figure 5(b) represents the current, respectively. Figure 6 shows the meminductance LML(LML = ϕ(t)/i(t)) curve.

Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
(a) Flux of meminductor; (b) current of meminductor.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
(a) Flux of meminductor; (b) current of meminductor.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
The meminductance curve for sinusoidal source.

6. Conclusions

We have demonstrated that the current-controlled meminductor can be transformed into memristor through the constitutive relation expanding. The mutator presented here provides a true MR-ML transformation. Using the procedure mentioned above, the memristor-to-memcapacitor mutator can also be easily designed. Together with the recently reported mutator, these circuits serve as useful tools for analyzing these new memory elements.

Acknowledgments

This work was supported in part by the National Natural Science Foundation of China under Grant 60974020, 60972155, the Natural Science Foundation of Chongqing under Grant CSTC2009BB2305, the Fundamental Research Funds for the Central Universities (Grant no. XDJK2010C023), and the National Science Foundation for Post-doctoral Scientists of China (Grant no. CPSF20100470116).

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.