A codimension-4 homoclinic bifurcation with one orbit flip and one inclination flip at principal eigenvalue direction resonance is considered. By introducing a local active coordinate system in some small neighborhood of homoclinic orbit, we get the Poincaré return map and the bifurcation equation. A detailed investigation produces the number and the existence of 1-homoclinic orbit, 1-periodic orbit, and double 1-periodic orbits. We also locate their bifurcation surfaces in certain regions.

1. Introduction and Hypotheses

The study of homoclinic flip bifurcations is comprehensively developed from the last two decades with the beginning work of Yanagida (1987) for homoclinic-doubling bifurcations. Generally there exist two kinds of homoclinic flips, namely the orbit flips and the inclination flips corresponding to nonprincipal homoclinic orbits or critically twisted homoclinic orbits, respectively. Kisaka et al. in [1, 2] and Naudot in [3] studied some cases of codimension two inclination flips; Morales and Pacifico in [4] and Naudot in [5] considered the orbit flips cases, while Homburg and Krauskopf in [6] proposed several unfoldings of the resonant homoclinic flip bifurcations around the central codimension-three point (the organizing centre) in parameter space to study the qualitative structure of bifurcation curves on a sphere and also that of Oldeman et al. in [7] by a numerical investigation with some software into these bifurcations in a specific three-dimensional vector field.

Recently, Zhang et al. in [8–10] studied a kind of multiple flips homoclinic resonant bifurcation and got the existence of some saddle-node bifurcations and homoclinic-doubling bifurcations. Meanwhile Geng et al. in [11], Lu et al. in [12], and Liu in [13] discussed, respectively, a heterodimensional cycle flip or accompanied by transcritical bifurcation; they found the double and triple periodic orbit bifurcations and gave also some coexistence conditions for homoclinic orbits and periodic orbits.

As mentioned in [6, 7], due to the break of three genericity conditions, there are many complicated homoclinic flips cases to study. In this paper, we confine our attention to a principal eigenvalue resonance of one orbit flip and one inclination flip homoclinic bifurcation. Compared with the above-mentioned work, our subject is very challenging and difficult because of the stronger degeneracy and the higher codimension. By constructing specifically a local active coordinate in a small tubular neighborhood of homoclinic orbit, we establish a regular map and then combine it with a singular map defined by the approximation solutions of system to build Poincaré return map (see also [14]). We obtain the existence of several 1-periodic orbit, 1-homoclinic orbit, and double 1-periodic orbits, as well as some bifurcation surfaces with the analysis of the bifurcation equation.

We first consider a C^r system

()

and its unperturbed system

()

where r ≥ 3, z ∈ ℝ⁴, μ ∈ ℝ^l, l ≥ 4, 0<|μ | ≪ 1, f(0) = 0, and g(0, μ) = g(z, 0) = 0. Suppose that the linearization Df(0) has four simple real eigenvalues λ₁, λ₂, −ρ₁, and −ρ₂ with λ₂ > λ₁ > 0 > −ρ₁ > −ρ₂. Accordingly, the stable manifold W^s and the unstable manifold W^u are both two-dimensional. Let W^ss and W^uu be the strong stable manifold and the strong unstable manifold of the saddle z = O, respectively. Assume further that system (2) has a homoclinic orbit Γ = {z = r(t) : t ∈ ℝ, r(±∞) = 0}. Hereinafter, our arguments will spread based on the following three hypotheses.

(H1) Resonance. λ₁(μ) = ρ₁(μ), |μ | ≪ 1, where λ₁(0) = λ₁ and ρ₁(0) = ρ₁.
(H2) Orbit Flip. Define ; ; then e⁺ ∈ T₀W^u and are unit eigenvectors corresponding to λ₁ and −ρ₂, respectively, where T₀W^u (resp., T₀W^ss) is the tangent space of the corresponding manifold W^u (resp., W^ss) at the saddle z = O.
(H3) Inclination Flip. Let and e⁻ be the unit eigenvectors corresponding to λ₂ and −ρ₁, respectively, and
()

Remark 1. Hypothesis (H2) is called an orbit flip because homoclinic orbit trends from the weak unstable manifold toward the strong stable manifold. Hypothesis (H3) means an inclination flip for its equivalence to

()

2. Poincaré Return Map

This section treats mainly the establishment of Poincaré return map with two steps. To begin we first need to transform system (1) into a normal form in some neighborhood of the origin O.

It is well known that there are always two C^r and C^r−1 transformations successively, also by the stable (or unstable) manifold theorem in [15], to straighten the local manifolds

and

, respectively,

(resp.,

); see [8–10]. Notice that now

and

, where z = (x, y, u, v) ∈ ℝ⁴ and u(0) = u^′(0) = 0. Thus, system (1) can be changed to a C^r−2 form in the neighborhood U as follows:

()

where H₁(x, 0,0) = 0, H₂(0, y, 0) = 0, λ₁(0) = λ₁, λ₂(0) = λ₂, ρ₁(0) = ρ₁, and ρ₂(0) = ρ₂. a(μ), b(μ), c(μ), and d(μ) are parameters depending on μ.

Owing to the above straightness of the invariant manifolds, it is easy to find some moment T, such that r(−T) = {δ, 0, δ_u, 0} and r(T) = {0,0, 0, δ} for some sufficiently small δ and |δ_u | = O(δ²) with {(x, y, u, v):|x | , |y | , |u | , |v | < 2δ} ⊂ U. Wherefore one can choose

()

as the cross-sections of Γ at t = T and t = −T, respectively. Let τ be the time going from q₀(x₀, y₀, u₀, v₀) ∈ S₀ to q₁(x₁, y₁, u₁, v₁) ∈ S₁ and the Silnikov time

, with the help of the linear approximation solutions of system (5) (see [8–10]); we have thereby

()

which give explicitly the definition of the local transition map F₀ : S₀ → S₁ : q₀ ↦ q₁; see Figure 1(a).

Details are in the caption following the image — **Figure 1 (a) F0: S0→S1**
Open in figure viewer PowerPoint

Transition maps.

In the following part we construct the map F₁ : S₁ → S₀. Firstly consider the linear variational system

()

and its adjoint system

()

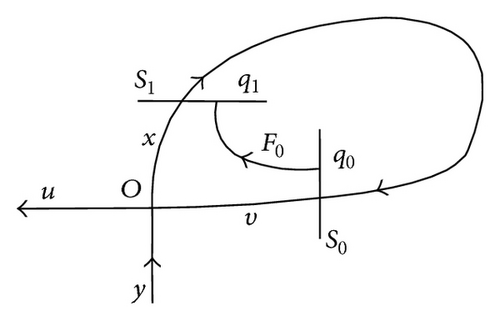
Lemma 2. There exists a fundamental solution matrix Z(t) = (z₁(t), z₂(t), z₃(t), z₄(t)) of system (8) satisfying

()

where z₁(t)∈(T_r(t)W^u) ^c∩(T_r(t)W^s) ^c,

, z₃(t) ∈ T_r(t)W^u, z₄(t) ∈ T_r(t)W^s and w₁₂w₂₁w₃₁w₄₄ ≠ 0, w₂₃ < 0. Moreover,

, i ≠ 2,

, i ≠ 4 for T → +∞.

Proof. Notice that the tangent subspace T_γ(−T)W^u is invariant and is straightened to be u axis; it is possible to choose z₃(−T) = (0,0, 1,0) since z₃(t) ∈ T_γ(t)W^u. While for w₃₁ ≠ 0, it is because and z₃(T) ∈ T_γ(T)W^u corresponding to x axis.

As to z_i(−T) or z_i(T), i = 1,2, 4, one may refer to [8, 9] for the similar proof, but we omit the details here.

Remark 3. The matrix (Z⁻¹(t)) ^* is a fundamental solution matrix of system (9). We denote it as Φ(t) = (ϕ₁(t), ϕ₂(t), ϕ₃(t), ϕ₄(t)) = (Z⁻¹(t)) ^*; then ϕ₁(t)∈(T_r(t)W^u) ^c∩(T_r(t)W^s) ^c is bounded and tends to zero exponentially as |t | →+∞ due to <ϕ_i(t), z_i(t) ≥ 1 and z_i(t) tends exponentially to infinity.

In fact (z₁(t), z₂(t), z₃(t), z₄(t)) can be regarded as a new local coordinate system along Γ. So we may make a coordinate change as

()

where N = N(t) = (n₁(t), 0, n₃(t), n₄(t)) ^*. Note that the new s(t) should satisfy system (1); that is,

()

An asymptotic expansion with respect to r(t) shows that

()

Via integrating both sides from −T to T of this equation, one can finally obtain

()

where

are the Melnikov vectors. And further

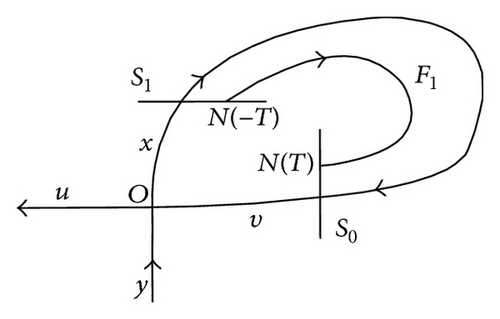
Equation (14) defines exactly the map F₁ : S₁ → S₀; N(−T) ↦ N(T) under the new coordinate system; see Figure 1(b).

In order to combine F₀ and F₁ into the Poincaré return map, we still need to establish a relationship between the original and the new coordinate systems. In doing so, recall that z(t) = r(t) + Z(t)N(t); then by taking time t = T and t = −T, respectively, together with z(T) = q_2j(x_2j,y_2j,u_2j,v_2j) ∈ S₀, z(−T) = q_2j+1(x_2j+1,y_2j+1,u_2j+1,v_2j+1) ∈ S₁ and N_2j(T) = (n_2j,1,0,n_2j,3,n_2j,4), N_2j+1(−T) = (n_2j+1,1,0,n_2j+1,3, n_2j+1,4), j = 0,1, 2, …, we obtain immediately the following formulas:

()

With all of the above, the Poincaré return map is given as F = F₁∘F₀. Therefore, the associated successor function G(s, u₁, y₀) = (G₁, G₃, G₄) = F(q₀) − q₀ is

()

3. Bifurcation Results

From the definition of the Silnikov time , we know that a solution with s > 0 of (16) or equivalently τ > 0 corresponds to a periodic orbit near Γ and a solution with s = 0 of (16) or equivalently τ = +∞ corresponds to a homoclinic orbit near Γ. It is enough to study the solutions of the successor function G(s, u₁, y₀) = 0 for bifurcation analysis. Consider for concision that we omit the dependence on parameter μ from now on in the exponent notation.

From G₃ = 0 and G₄ = 0, there are

()

Put u₁ and y₀ into G₁ = 0; we have

()

which is the bifurcation equation. Furthermore, for w₃₃ ≠ 0,

()

where

. Implicit function theorem reveals that (16) has a unique solution as

()

with s(0) = 0, u₁(0) = 0, and y₀(0) = 0. It means that system (1) has a unique periodic orbit as s > 0 or a unique homoclinic orbit as s = 0, and they cannot coexist.

Theorem 4. Suppose that M₁ ≠ 0 and w₃₃ ≠ 0 are true; then system (1) has a unique 1-periodic orbit near Γ for w₃₁w₃₃M₁μ < 0 or has a unique 1-homoclinic orbit Γ_μ near Γ as , and they do not coexist.

Proof. Clearly F(s, μ) = 0 has a small positive solution ., for w₃₁w₃₃M₁μ < 0, and has a zero solution s = 0 for μ ∈ H¹ which is a codimension-one hypersurface.

In the following part we restrict our attention on the case w₃₃ = 0 for 2λ₁ > λ₂ > ρ₂. Define

()

where k, l = 0,1, i = 1,3, j = 1,3, 4.

In order to well solve (18), we rewrite it into two parts, namely, a line W = P(s, μ) and a curve W = Q(s, μ) with respect to s:

()

Then there are firstly the following conclusions based on an analysis of the relative position of the line W = P(s, μ) and the curve W = Q(s, μ).

Lemma 5. Suppose that 2λ₁ > λ₂ > ρ₂, w₃₃ = 0, and w₄₂ ≠ 0 hold; then F(s, μ) = 0 has a unique small positive solution for , where .

Proof. It is clear that

()

Therefore, the line W = P(s, μ) intersects the curve W = Q(s, μ) at a unique point

for

. Notice that Q(s^*, μ) = 2w₁₂M₁μ + M₄μ + h.o.t.>w₁₂M₁μ + M₄μs^* + h.o.t. = P(s^*, μ), so

Theorem 6. Suppose that 2λ₁ > λ₂ > ρ₂, w₃₃ = 0, and w₄₂ ≠ 0 hold; then system (1) has exactly a unique (resp., not any) 1-periodic orbit for (resp., ).

Proof. From Lemma 5, we know that F(s, μ) = 0 has exactly a unique small positive solution for which corresponds exactly to a 1-periodic orbit of system (1). Moreover, F(s, μ) = 0 does not have any small positive solutions for .

Theorem 7. Suppose that 2λ₁ > λ₂ > ρ₂, w₃₃ = 0, and w₄₂ ≠ 0 hold; then, for and Rank (M₁, M₄) = 2, system (1) has a unique double 1-periodic orbit near Γ on the bifurcation surface

()

which has a normal vector M₁ at μ = 0. The corresponding double positive zero point is

()

(see Figure 2(a)).

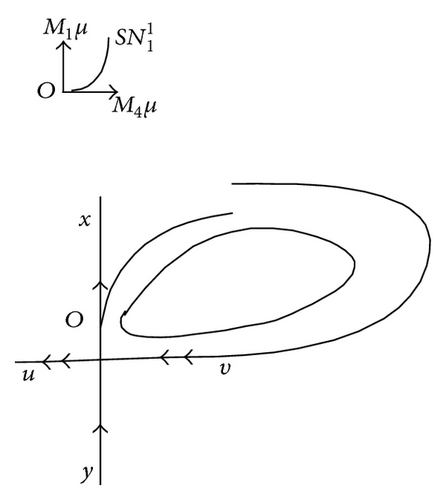
Proof. We know that the existence of a double 1-periodic orbit corresponds to the equations P(s, μ) = Q(s, μ), P^′(s, μ) = Q^′(s, μ), and P^′′(s, μ) ≠ Q^′′(s, μ), that is,

()

having solutions. Indeed, the second equation of (26) permits the double positive zero point s_* as

. Putting it into the first equation of (26), there is

()

Then SN¹ exists for

From the above proof, we see that, when M₄μ > 0 and w₁₂M₁μ < 0, the line W = P(s, μ) has a positive slope lying under the curve W = Q(s, μ) when w₄₂w₄₄ > 0, so if w₁₂M₁μ increases, the line must intersect the curve at two sufficiently small positive points, which can be equal to the existence of two 1-periodic orbits of system (1). For M₄μ < 0, w₄₂w₄₄ < 0, and w₁₂M₁μ > 0, the arguments are similar. So we have immediately a complement of Theorem 7.

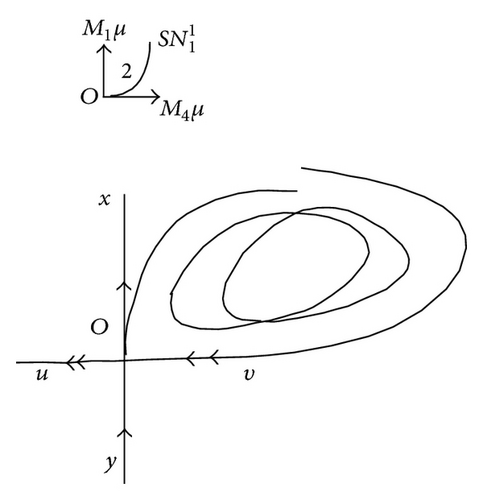
Corollary 8. Assume that the hypotheses of Theorem 7 are valid, system (1) then has two (resp., not any) 1-periodic orbits near Γ when μ lies on the side of SN¹ which points to the direction (sgn w₁₂w₄₂w₄₄) M₁ (resp., in the opposite direction) (see Figures 2(b) and 2(c)).

As Melnikov functions generally play an important role in bifurcation study, the following theorem shows also the existence of some double 1-periodic orbits relying on the investigation of M_i = 0 for i = 1,3, 4.

Theorem 9. Suppose 2λ₁ > λ₂ > ρ₂, w₃₃ = 0, and w₄₂ ≠ 0 are valid; then the following applies.

(1)
For M₁ = 0 or , system (1) has exactly one 1-homoclinic orbit and one (resp., not any) 1-periodic orbit near Γ and they (resp., do not) coexist as (resp., ).
(2)
For M₃ = 0, system (1) has exactly one (resp., not any) 1-periodic orbit near Γ as (resp., ).
system (1) has a unique double 1-periodic orbit near Γ as and Rank (M₁, M₄) = 2. Accordingly, the double 1-periodic orbit bifurcation surface is with a normal vector M₁ at μ = 0, and it may generate two 1-periodic orbits when μ lies in the direction (sgn w₄₂w₄₄w₁₂)M₁ of SN¹ and no such a 1-periodic orbit in the opposite direction.
(3)
For M₄ = 0 or , system (1) has only one (resp. not any) 1-periodic orbit near Γ as (resp., ).
(4)
For , system (1) does not have any 1-periodic orbit near Γ.
(5)
For , system (1) has only one 1-homoclinic orbit near Γ.

Proof. When M₁ = 0 or M₁ = M₃ = 0, has two solutions s₁ = 0 and . for which correspond to a 1-periodic orbit, and a 1-homoclinic orbit respectively. Thus, (1) is true.

The result of the cases (2) is exactly the same as that of Theorem 7.

If M₄ = 0 or M₃ = M₄ = 0, F(s, μ) = 0 has only a positive solution . for , which means system (1) has a 1-periodic orbit. Then (3) is valid.

In case of , it is clear that F(s, μ) = 0 does not have any small nonnegative solutions, so system (1) does not have, any 1-homoclinic orbits or 1-periodic orbits.

The last conclusion is obvious. Thereby, the proof is complete.

Remark 10. Notice that, in Theorem 9 (1) and (5), F(s, μ) = 0 has a solution s = 0, which means that system (1) has a codimension-1 1-homoclinic orbit (see Figure 3(a)), so the existing homoclinic orbit is no longer orbit flip for y₀ = M₄μ + h.o.t.≠0. But if y₀ = 0, an orbit flip homoclinic orbit could still exist, where y₀ is given by G₄ = 0; see Figure 3(b).

Remark 11. There still exist some double 1-periodic orbits or triple 1-periodic orbits for the case w₄₂ = 0 and δ_u ≠ 0; one may pursue the similar process to discuss, so we leave it here.

Acknowledgment

The project is supported by the National Natural Science Foundation of China (no. 11126097).

References

1 Kisaka M., Kokubu H., and Oka H., Bifurcations to N-homoclinic orbits and N-periodic orbits in vector fields, Journal of Dynamics and Differential Equations. (1993) 5, no. 2, 305–357, https://doi.org/10.1007/BF01053164, MR1223451.
10.1007/BF01053164
Google Scholar
2 Kisaka M., Kokubu H., and Oka H., Supplement to homoclinic-doubling bifurcation in vector fields, Handbook of Dynamical Systems, 1993, 92–116.
Google Scholar
3 Naudot V., Strange attractor in the unfolding of an inclination-flip homoclinic orbit, Ergodic Theory and Dynamical Systems. (1996) 16, no. 5, 1071–1086, https://doi.org/10.1017/S014338570001018X, MR1417774, ZBL0866.58045.
10.1017/S014338570001018X
Web of Science® Google Scholar
4 Morales C. A. and Pacifico M. J., Inclination-flip homoclinic orbits arising from orbit-flip, Nonlinearity. (2001) 14, no. 2, 379–393, https://doi.org/10.1088/0951-7715/14/2/311, MR1819803, ZBL1026.37045.
10.1088/0951-7715/14/2/311
Web of Science® Google Scholar
5 Naudot V., A strange attractor in the unfolding of an orbit-flip homoclinic orbit, Dynamical Systems. (2002) 17, no. 1, 45–63, https://doi.org/10.1080/14689360110104563, MR1888697, ZBL1184.37029.
10.1080/14689360110104563
Google Scholar
6 Homburg A. J. and Krauskopf B., Resonant homoclinic flip bifurcations, Journal of Dynamics and Differential Equations. (2000) 12, no. 4, 807–850, https://doi.org/10.1023/A:1009046621861, MR1826963, ZBL0990.37038.
10.1023/A:1009046621861
Google Scholar
7 Oldeman B. E., Krauskopf B., and Champneys A. R., Numerical unfoldings of codimension-three resonant homoclinic flip bifurcations, Nonlinearity. (2001) 14, no. 3, 597–621, https://doi.org/10.1088/0951-7715/14/3/309, MR1830909, ZBL0990.37039.
10.1088/0951-7715/14/3/309
Web of Science® Google Scholar
8 Zhang T. S. and Zhu D. M., Homoclinic bifurcation of orbit flip with resonant principal eigenvalues, Acta Mathematica Sinica. (2006) 22, no. 3, 855–864, https://doi.org/10.1007/s10114-005-0581-x, MR2220179, ZBL1106.37013.
10.1007/s10114-005-0581-x
Web of Science® Google Scholar
9 Zhang T. and Zhu D., Bifurcations of homoclinic orbit connecting two nonleading eigendirections, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2007) 17, no. 3, 823–836, https://doi.org/10.1142/S0218127407017574, MR2324982, ZBL1140.37346.
10.1142/S0218127407017574
Web of Science® Google Scholar
10 Zhang T. S. and Zhu D. M., Bifurcation analysis of homoclinic flips at principal eigenvalues resonance, Applied Mathematics. (2013) 4, 271–278.
10.4236/am.2013.42041
Google Scholar
11 Geng F., Liu D., and Zhu D., Bifurcations of generic heteroclinic loop accompanied by transcritical bifurcation, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2008) 18, no. 4, 1069–1083, https://doi.org/10.1142/S0218127408020847, MR2422923, ZBL1147.34324.
10.1142/S0218127408020847
Web of Science® Google Scholar
12 Lu Q., Qiao Z., Zhang T., and Zhu D., Heterodimensional cycle bifurcation with orbit-flip, International Journal of Bifurcation and Chaos in Applied Sciences and Engineering. (2010) 20, no. 2, 491–508, https://doi.org/10.1142/S0218127410025569, MR2662042, ZBL1188.34044.
10.1142/S0218127410025569
Web of Science® Google Scholar
13 Liu X., Homoclinic flip bifurcations accompanied by transcritical bifurcation, Chinese Annals of Mathematics B. (2011) 32, no. 6, 905–916, https://doi.org/10.1007/s11401-011-0675-y, MR2852311, ZBL1271.34046.
10.1007/s11401-011-0675-y
CAS Web of Science® Google Scholar
14 Zhu D. and Xia Z., Bifurcations of heteroclinic loops, Science in China A. (1998) 41, no. 8, 837–848, https://doi.org/10.1007/BF02871667, MR1667063, ZBL0993.34040.
10.1007/BF02871667
Google Scholar
15 Wiggins S., Global Bifurcations and Chaos, 1988, 73, Springer, New York, NY, USA, https://doi.org/10.1007/978-1-4612-1042-9, MR956468.
10.1007/978-1-4612-1042-9
Google Scholar

All articles

Resonant Homoclinic Flips Bifurcation in Principal Eigendirections

Abstract

1. Introduction and Hypotheses

2. Poincaré Return Map

3. Bifurcation Results

Acknowledgment

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Resonant Homoclinic Flips Bifurcation in Principal Eigendirections

Abstract

1. Introduction and Hypotheses

2. Poincaré Return Map

3. Bifurcation Results

Acknowledgment

References

Figures

References

Related

Information