Volume 2013, Issue 1 217540

Research Article

Open Access

An Efficient Algorithm for the Reflexive Solution of the Quaternion Matrix Equation AXB + CX^HD = F

Ning Li

Department of Mathematics, Shanghai University, Shanghai 200444, China shu.edu.cn

School of Mathematics and Quantitative Economics, Shandong University of Finance and Economics, Jinan 250002, China sdfi.edu.cn

Search for more papers by this author

Qing-Wen Wang,

Corresponding Author

Qing-Wen Wang

[email protected]

Department of Mathematics, Shanghai University, Shanghai 200444, China shu.edu.cn

Search for more papers by this author

Jing Jiang,

Jing Jiang

Department of Mathematics, Qilu Normal University, Jinan 250013, China chinagate.cn

Search for more papers by this author

Ning Li,

Ning Li

Department of Mathematics, Shanghai University, Shanghai 200444, China shu.edu.cn

School of Mathematics and Quantitative Economics, Shandong University of Finance and Economics, Jinan 250002, China sdfi.edu.cn

Search for more papers by this author

Qing-Wen Wang,

Corresponding Author

Qing-Wen Wang

[email protected]

Department of Mathematics, Shanghai University, Shanghai 200444, China shu.edu.cn

Search for more papers by this author

Jing Jiang,

Jing Jiang

Department of Mathematics, Qilu Normal University, Jinan 250013, China chinagate.cn

Search for more papers by this author

First published: 24 February 2013

https://doi.org/10.1155/2013/217540

Citations: 2

Academic Editor: P. N. Shivakumar

Share a link

Email
Wechat
Bluesky

Abstract

We propose an iterative algorithm for solving the reflexive solution of the quaternion matrix equation AXB + CX^HD = F. When the matrix equation is consistent over reflexive matrix X, a reflexive solution can be obtained within finite iteration steps in the absence of roundoff errors. By the proposed iterative algorithm, the least Frobenius norm reflexive solution of the matrix equation can be derived when an appropriate initial iterative matrix is chosen. Furthermore, the optimal approximate reflexive solution to a given reflexive matrix X₀ can be derived by finding the least Frobenius norm reflexive solution of a new corresponding quaternion matrix equation. Finally, two numerical examples are given to illustrate the efficiency of the proposed methods.

1. Introduction

Throughout the paper, the notations ℝ^m×n and ℍ^m×n represent the set of all m × n real matrices and the set of all m × n matrices over the quaternion algebra ℍ = {a₁ + a₂i + a₃j + a₄k∣i² = j² = k² = ijk = −1, a₁, a₂, a₃, a₄ ∈ ℝ}. We denote the identity matrix with the appropriate size by I. We denote the conjugate transpose, the transpose, the conjugate, the trace, the column space, the real part, the mn × 1 vector formed by the vertical concatenation of the respective columns of a matrix A by , respectively. The Frobenius norm of A is denoted by ∥A∥, that is, . Moreover, A ⊗ B and A⊙B stand for the Kronecker matrix product and Hadmard matrix product of the matrices A and B.

Let Q ∈ ℍ^n×n be a generalized reflection matrix, that is, Q² = I and Q^H = Q. A matrix A is called reflexive with respect to the generalized reflection matrix Q, if A = QAQ. It is obvious that any matrix is reflexive with respect to I. Let ℝℍ^n×n(Q) denote the set of order n reflexive matrices with respect to Q. The reflexive matrices with respect to a generalized reflection matrix Q have been widely used in engineering and scientific computations [1, 2].

In the field of matrix algebra, quaternion matrix equations have received much attention. Wang et al. [3] gave necessary and sufficient conditions for the existence and the representations of P-symmetric and P-skew-symmetric solutions of quaternion matrix equations A_aX = C_a and A_bXB_b = C_b. Yuan and Wang [4] derived the expressions of the least squares η-Hermitian solution with the least norm and the expressions of the least squares anti-η-Hermitian solution with the least norm for the quaternion matrix equation AXB + CXD = E. Jiang and Wei [5] derived the explicit solution of the quaternion matrix equation . Li and Wu [6] gave the expressions of symmetric and skew-antisymmetric solutions of the quaternion matrix equations A₁X = C₁ and XB₃ = C₃. Feng and Cheng [7] gave a clear description of the solution set of the quaternion matrix equation .

The iterative method is a very important method to solve matrix equations. Peng [8] constructed a finite iteration method to solve the least squares symmetric solutions of linear matrix equation AXB = C. Also Peng [9–11] presented several efficient iteration methods to solve the constrained least squares solutions of linear matrix equations AXB = C and AXB + CYD = E, by using Paige’s algorithm [12] as the frame method. Duan et al. [13–17] proposed iterative algorithms for the (Hermitian) positive definite solutions of some nonlinear matrix equations. Ding et al. proposed the hierarchical gradient-based iterative algorithms [18] and hierarchical least squares iterative algorithms [19] for solving general (coupled) matrix equations, based on the hierarchical identification principle [20]. Wang et al. [21] proposed an iterative method for the least squares minimum-norm symmetric solution of AXB = E. Dehghan and Hajarian constructed finite iterative algorithms to solve several linear matrix equations over (anti)reflexive [22–24], generalized centrosymmetric [25, 26], and generalized bisymmetric [27, 28] matrices. Recently, Wu et al. [29–31] proposed iterative algorithms for solving various complex matrix equations.

However, to the best of our knowledge, there has been little information on iterative methods for finding a solution of a quaternion matrix equation. Due to the noncommutative multiplication of quaternions, the study of quaternion matrix equations is more complex than that of real and complex equations. Motivated by the work mentioned above and keeping the interests and wide applications of quaternion matrices in view (e.g., [32–45]), we, in this paper, consider an iterative algorithm for the following two problems.

Problem 1. For given matrices A, C ∈ ℍ^m×n, B, D ∈ ℍ^n×p, F ∈ ℍ^m×p and the generalized reflection matrix Q, find X ∈ ℝℍ^n×n(Q), such that

(1)

Problem 2. When Problem 1 is consistent, let its solution set be denoted by S_H. For a given reflexive matrix X₀ ∈ ℝℍ^n×n(Q), find , such that

(2)

The remainder of this paper is organized as follows. In Section 2, we give some preliminaries. In Section 3, we introduce an iterative algorithm for solving Problem 1. Then we prove that the given algorithm can be used to obtain a reflexive solution for any initial matrix within finite steps in the absence of roundoff errors. Also we prove that the least Frobenius norm reflexive solution can be obtained by choosing a special kind of initial matrix. In addition, the optimal reflexive solution of Problem 2 by finding the least Frobenius norm reflexive solution of a new matrix equation is given. In Section 4, we give two numerical examples to illustrate our results. In Section 5, we give some conclusions to end this paper.

2. Preliminary

In this section, we provide some results which will play important roles in this paper. First, we give a real inner product for the space ℍ^m×n over the real field ℝ.

Theorem 3. In the space ℍ^m×n over the field ℝ, a real inner product can be defined as

(3)

for A, B ∈ ℍ^m×n. This real inner product space is denoted as (ℍ^m×n, ℝ, 〈·, ·〉).

Proof. (1) For A ∈ ℍ^m×n, let A = A₁ + A₂i + A₃j + A₄k, then

(4)

It is obvious that 〈A, A〉 > 0 and 〈A, A〉 = 0⇔A = 0.

(2) For A, B ∈ ℍ^m×n, let A = A₁ + A₂i + A₃j + A₄k and B = B₁ + B₂i + B₃j + B₄k, then we have

(5)

(3) For A, B, C ∈ ℍ^m×n

(6)

(4) For A, B ∈ ℍ^m×n and a ∈ ℝ,

(7)

All the above arguments reveal that the space ℍ^m×n over field ℝ with the inner product defined in (3) is an inner product space.

Let ∥·∥_Δ represent the matrix norm induced by the inner product 〈·, ·〉. For an arbitrary quaternion matrix A ∈ ℍ^m×n, it is obvious that the following equalities hold:

(8)

which reveals that the induced matrix norm is exactly the Frobenius norm. For convenience, we still use ∥·∥ to denote the induced matrix norm.

Let E_ij denote the m × n quaternion matrix whose (i, j) entry is 1, and the other elements are zeros. In inner product space (ℍ^m×n, ℝ, 〈·, ·〉), it is easy to verify that E_ij, E_iji, E_ijj, E_ijk, i = 1, 2, …, m, j = 1, 2, …, n, is an orthonormal basis, which reveals that the dimension of the inner product space (ℍ^m×n, ℝ, 〈·, ·〉) is 4mn.

Next, we introduce a real representation of a quaternion matrix.

For an arbitrary quaternion matrix M = M₁ + M₂i + M₃j + M₄k, a map ϕ(·), from ℍ^m×n to ℝ^4m×4n, can be defined as

(9)

Lemma 4 (see [41].)Let M and N be two arbitrary quaternion matrices with appropriate size. The map ϕ(·) defined by (9) satisfies the following properties.

(a)
M = N⇔ϕ(M) = ϕ(N).
(b)
ϕ(M + N) = ϕ(M) + ϕ(N), ϕ(MN) = ϕ(M)ϕ(N), ϕ(kM) = kϕ(M), k ∈ ℝ.
(c)
ϕ(M^H) = ϕ^T(M).
(d)
, where
(10)

By (9), it is easy to verify that

(11)

Finally, we introduce the commutation matrix.

A commutation matrix P(m, n) is a mn × mn matrix which has the following explicit form:

(12)

Moreover, P(m, n) is a permutation matrix and P(m, n) = P^T(n, m) = P⁻¹(n, m). We have the following lemmas on the commutation matrix.

Lemma 5 (see [46].)Let A be a m × n matrix. There is a commutation matrix P(m, n) such that

(13)

Lemma 6 (see [46].)Let A be a m × n matrix and B a p × q matrix. There exist two commutation matrices P(m, p) and P(n, q) such that

(14)

3. Main Results

3.1. The Solution of Problem 1

In this subsection, we will construct an algorithm for solving Problem 1. Then some lemmas will be given to analyse the properties of the proposed algorithm. Using these lemmas, we prove that the proposed algorithm is convergent.

Algorithm 7 (Iterative algorithm for Problem 1).

(1)
Choose an initial matrix X(1) ∈ ℝℍ^n×n(Q).
(2)
Calculate
(15)
(3)
If R(k) = 0, then stop and X(k) is the solution of Problem 1; else if R(k) ≠ 0 and P(k) = 0, then stop and Problem 1 is not consistent; else k : = k + 1.
(4)
Calculate
(16)
(5)
Go to Step (3).

Lemma 8. Assume that the sequences {R(i)} and {P(i)} are generated by Algorithm 7, then 〈R(i), R(j)〉 = 0 and 〈P(i), P(j)〉 = 0 for i, j = 1, 2, …, i ≠ j.

Proof. Since 〈R(i), R(j)〉 = 〈R(j), R(i)〉 and 〈P(i), P(j)〉 = 〈P(j), P(i)〉 for i, j = 1, 2, …, we only need to prove that 〈R(i), R(j)〉 = 0 and 〈P(i), P(j)〉 = 0 for 1 ≤ i < j.

Now we prove this conclusion by induction.

Step 1. We show that

(17)

We also prove (17) by induction. When i = 1, we have

(18)

Also we can write

(19)

Now assume that conclusion (17) holds for 1 ≤ i ≤ s − 1, then

(20)

And it can also be obtained that

(21)

Therefore, the conclusion (17) holds for i = 1, 2, ….

Step 2. Assume that 〈R(i), R(i + r)〉 = 0 and 〈P(i), P(i + r)〉 = 0 for i ≥ 1 and r ≥ 1. We will show that

(22)

We prove the conclusion (22) in two substeps.

Substep 2.1. In this substep, we show that

(23)

It follows from Algorithm 7 that

(24)

Also we can write

(25)

Substep 2.2. In this substep, we prove the conclusion (22) in Step 2. It follows from Algorithm 7 that

(26)

Repeating the above process (26), we can obtain

(27)

Combining these two relations with (24) and (25), it implies that (22) holds. So, by the principle of induction, we know that Lemma 8 holds.

Lemma 9. Assume that Problem 1 is consistent, and let be its solution. Then, for any initial matrix X(1) ∈ ℝℍ^n×n(Q), the sequences {R(i)}, {P(i)}, and {X(i)} generated by Algorithm 7 satisfy

(28)

Proof. We also prove this conclusion by induction.

When i = 1, it follows from Algorithm 7 that

(29)

This implies that (28) holds for i = 1.

Now it is assumed that (28) holds for i = s, that is

(30)

Then, when i = s + 1

(31)

Therefore, Lemma 9 holds by the principle of induction.

From the above two lemmas, we have the following conclusions.

Remark 10. If there exists a positive number i such that R(i) ≠ 0 and P(i) = 0, then we can get from Lemma 9 that Problem 1 is not consistent. Hence, the solvability of Problem 1 can be determined by Algorithm 7 automatically in the absence of roundoff errors.

Theorem 11. Suppose that Problem 1 is consistent. Then for any initial matrix X(1) ∈ ℝℍ^n×n(Q), a solution of Problem 1 can be obtained within finite iteration steps in the absence of roundoff errors.

Proof. In Section 2, it is known that the inner product space (ℍ^m×p, R, 〈·, ·〉) is 4mp-dimensional. According to Lemma 9, if R(i) ≠ 0, i = 1, 2, …, 4mp, then we have P(i) ≠ 0, i = 1, 2, …, 4mp. Hence R(4mp + 1) and P(4mp + 1) can be computed. From Lemma 8, it is not difficult to get

(32)

Then R(1), R(2), …, R(4mp) is an orthogonal basis of the inner product space (ℍ^m×p, R, 〈·, ·〉). In addition, we can get from Lemma 8 that

(33)

It follows that R(4mp + 1) = 0, which implies that X(4mp + 1) is a solution of Problem 1.

3.2. The Solution of Problem 2

In this subsection, firstly we introduce some lemmas. Then, we will prove that the least Frobenius norm reflexive solution of (1) can be derived by choosing a suitable initial iterative matrix. Finally, we solve Problem 2 by finding the least Frobenius norm reflexive solution of a new-constructed quaternion matrix equation.

Lemma 12 (see [47].)Assume that the consistent system of linear equations My = b has a solution y₀ ∈ R(M^T) then y₀ is the unique least Frobenius norm solution of the system of linear equations.

Lemma 13. Problem 1 is consistent if and only if the system of quaternion matrix equations

(34)

is consistent. Furthermore, if the solution sets of Problem 1 and (34) are denoted by S_H and

, respectively, then, we have

Proof. First, we assume that Problem 1 has a solution X. By AXB + CX^HD = F and QXQ = X, we can obtain AXB + CX^HD = F and AQXQB + CQX^HQD = F, which implies that X is a solution of quaternion matrix equations (34), and .

Conversely, suppose (34) is consistent. Let X be a solution of (34). Set X_a = (X + QXQ)/2. It is obvious that X_a∈ℝℍ^n×n(Q). Now we can write

(35)

Hence X_a is a solution of Problem 1. The proof is completed.

Lemma 14. The system of quaternion matrix equations (34) is consistent if and only if the system of real matrix equations

(36)

is consistent, where X_ij ∈ ℍ^n×n, i, j = 1, 2, 3, 4, are submatrices of the unknown matrix. Furthermore, if the solution sets of (34) and (36) are denoted by

and

, respectively, then, we have

Proof. Suppose that (34) has a solution

(37)

Applying (a), (b), and (c) in Lemma 4 to (34) yields

(38)

which implies that ϕ(X) is a solution of (36) and

. Conversely, suppose that (36) has a solution

(39)

By (d) in Lemma 4, we have that

(40)

Hence

(41)

which implies that

, and

are also solutions of (36). Thus,

(42)

is also a solution of (36), where

(43)

Let

(44)

Then it is not difficult to verify that

(45)

We have that

is a solution of (34) by (a) in Lemma 4. The proof is completed.

Lemma 15. There exists a permutation matrix P(4n,4n) such that (36) is equivalent to

(46)

Lemma 15 is easily proven through Lemma 5. So we omit it here.

Theorem 16. When Problem 1 is consistent, let its solution set be denoted by S_H. If , and can be expressed as

(47)

then,

is the least Frobenius norm solution of Problem 1.

Proof. By (a), (b), and (c) in Lemmas 4, 5, and 6, we have that

(48)

By Lemma 12,

is the least Frobenius norm solution of matrix equations (46).

Noting (11), we derive from Lemmas 13, 14, and 15 that is the least Frobenius norm solution of Problem 1.

From Algorithm 7, it is obvious that, if we consider

(49)

then all X(k) generated by Algorithm 7 can be expressed as

(50)

Using the above conclusion and considering Theorem 16, we propose the following theorem.

Theorem 17. Suppose that Problem 1 is consistent. Let the initial iteration matrix be

(51)

where G is an arbitrary quaternion matrix, or especially, X(1) = 0, then the solution X^*, generated by Algorithm 7, is the least Frobenius norm solution of Problem 1.

Now we study Problem 2. When Problem 1 is consistent, the solution set of Problem 1 denoted by S_H is not empty. Then, For a given reflexive matrix X₀ ∈ ℝℍ^n×n(Q),

(52)

Let

and

, then Problem 2 is equivalent to finding the least Frobenius norm reflexive solution of the quaternion matrix equation

(53)

By using Algorithm 7, let the initial iteration matrix

, where G is an arbitrary quaternion matrix in ℍ^m×p, or especially,

, we can obtain the least Frobenius norm reflexive solution

of (53). Then we can obtain the solution of Problem 2, which is

(54)

4. Examples

In this section, we give two examples to illustrate the efficiency of the theoretical results.

Example 18. Consider the quaternion matrix equation

(55)

with

(56)

We apply Algorithm 7 to find the reflexive solution with respect to the generalized reflection matrix.

(57)

For the initial matrix X(1) = Q, we obtain a solution, that is

(58)

with corresponding residual ∥R(20)∥ = 2.2775 × 10⁻¹¹. The convergence curve for the Frobenius norm of the residuals R(k) is given in Figure 1, where r(k) = ∥R(k)∥.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The convergence curve for the Frobenius norm of the residuals from Example 18.

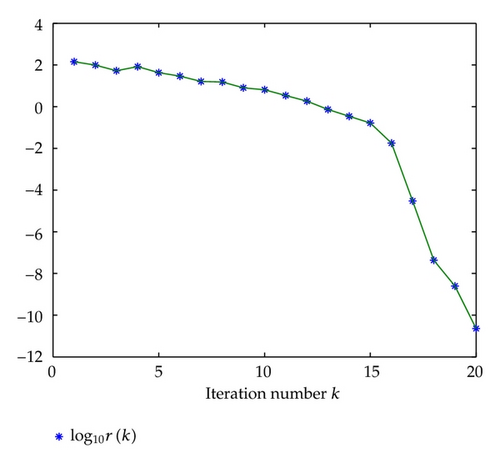
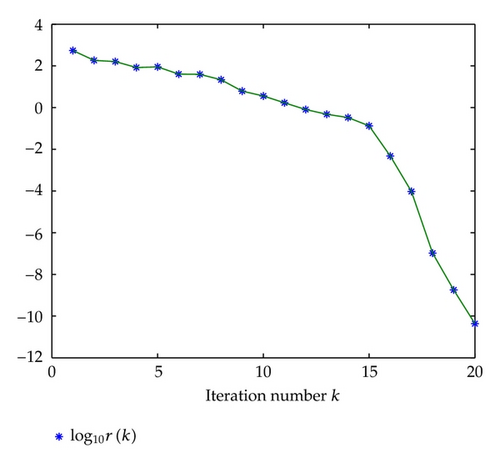
Example 19. In this example, we choose the matrices A, B, C, D, F, and Q as same as in Example 18. Let

(59)

In order to find the optimal approximation reflexive solution to the given matrix X₀, let

and

. Now we can obtain the least Frobenius norm reflexive solution

of the quaternion matrix equation

, by choosing the initial matrix

, that is

(60)

with corresponding residual . The convergence curve for the Frobenius norm of the residuals is given in Figure 2, where .

Therefore, the optimal approximation reflexive solution to the given matrix X₀ is

(61)

The results show that Algorithm 7 is quite efficient.

5. Conclusions

In this paper, an algorithm has been presented for solving the reflexive solution of the quaternion matrix equation AXB + CX^HD = F. By this algorithm, the solvability of the problem can be determined automatically. Also, when the quaternion matrix equation AXB + CX^HD = F is consistent over reflexive matrix X, for any reflexive initial iterative matrix, a reflexive solution can be obtained within finite iteration steps in the absence of roundoff errors. It has been proven that by choosing a suitable initial iterative matrix, we can derive the least Frobenius norm reflexive solution of the quaternion matrix equation AXB + CX^HD = F through Algorithm 7. Furthermore, by using Algorithm 7, we solved Problem 2. Finally, two numerical examples were given to show the efficiency of the presented algorithm.

Acknowledgments

This research was supported by Grants from Innovation Program of Shanghai Municipal Education Commission (13ZZ080), the National Natural Science Foundation of China (11171205), the Natural Science Foundation of Shanghai (11ZR1412500), the Discipline Project at the corresponding level of Shanghai (A. 13-0101-12-005), and Shanghai Leading Academic Discipline Project (J50101).

References

1 Chen H. C. and Sameh A. H., A matrix decomposition method for orthotropic elasticity problems, SIAM Journal on Matrix Analysis and Applications. (1989) 10, no. 1, 39–64, https://doi.org/10.1137/0610004, 976151, ZBL0669.73010.
10.1137/0610004
Web of Science® Google Scholar
2 Chen H. C., Generalized reflexive matrices: special properties and applications, SIAM Journal on Matrix Analysis and Applications. (1998) 19, no. 1, 140–153, https://doi.org/10.1137/S0895479895288759, 1609944, ZBL0910.15005.
10.1137/S0895479895288759
Web of Science® Google Scholar
3 Wang Q. W., Chang H. X., and Lin C. Y., P-(skew)symmetric common solutions to a pair of quaternion matrix equations, Applied Mathematics and Computation. (2008) 195, no. 2, 721–732, https://doi.org/10.1016/j.amc.2007.05.021, 2381251, ZBL1149.15011.
10.1016/j.amc.2007.05.021
Web of Science® Google Scholar
4 Yuan S. F. and Wang Q. W., Two special kinds of least squares solutions for the quaternion matrix equation AXB + CXD = E, Electronic Journal of Linear Algebra. (2012) 23, 257–274, 2889586, ZBL1250.65051.
10.13001/1081-3810.1519
Web of Science® Google Scholar
5 Jiang T. S. and Wei M. S., On a solution of the quaternion matrix equation and its application, Acta Mathematica Sinica (English Series). (2005) 21, no. 3, 483–490, https://doi.org/10.1007/s10114-004-0428-x, 2145901, ZBL1083.15019.
10.1007/s10114-004-0428-x
Web of Science® Google Scholar
6 Li Y. T. and Wu W. J., Symmetric and skew-antisymmetric solutions to systems of real quaternion matrix equations, Computers & Mathematics with Applications. (2008) 55, no. 6, 1142–1147, https://doi.org/10.1016/j.camwa.2007.06.015, 2394352, ZBL1143.15012.
10.1016/j.camwa.2007.06.015
Web of Science® Google Scholar
7 Feng L. G. and Cheng W., The solution set to the quaternion matrix equation , Algebra Colloquium. (2012) 19, no. 1, 175–180, 2876851, ZBL1236.15032.
10.1142/S1005386712000132
Web of Science® Google Scholar
8 Peng Z. Y., An iterative method for the least squares symmetric solution of the linear matrix equation AXB = C, Applied Mathematics and Computation. (2005) 170, no. 1, 711–723, https://doi.org/10.1016/j.amc.2004.12.032, 2177574, ZBL1081.65039.
10.1016/j.amc.2004.12.032
Web of Science® Google Scholar
9 Peng Z. Y., A matrix LSQR iterative method to solve matrix equation AXB = C, International Journal of Computer Mathematics. (2010) 87, no. 8, 1820–1830, https://doi.org/10.1080/00207160802516875, 2665753, ZBL1195.65056.
10.1080/00207160802516875
Web of Science® Google Scholar
10 Peng Z. Y., New matrix iterative methods for constraint solutions of the matrix equation AXB = C, Journal of Computational and Applied Mathematics. (2010) 235, no. 3, 726–735, https://doi.org/10.1016/j.cam.2010.07.001, 2719811, ZBL1206.65145.
10.1016/j.cam.2010.07.001
Web of Science® Google Scholar
11 Peng Z. Y., Solutions of symmetry-constrained least-squares problems, Numerical Linear Algebra with Applications. (2008) 15, no. 4, 373–389, https://doi.org/10.1002/nla.578, 2413779, ZBL1212.65181.
10.1002/nla.578
Web of Science® Google Scholar
12 Paige C. C., Bidiagonalization of matrices and solutions of the linear equations, SIAM Journal on Numerical Analysis. (1974) 11, 197–209, 0341842, https://doi.org/10.1137/0711019.
10.1137/0711019
Web of Science® Google Scholar
13 Duan X. F., Liao A. P., and Tang B., On the nonlinear matrix equation , Linear Algebra and Its Applications. (2008) 429, no. 1, 110–121, https://doi.org/10.1016/j.laa.2008.02.014, 2419144, ZBL1148.15012.
10.1016/j.laa.2008.02.014
Web of Science® Google Scholar
14 Duan X. F. and Liao A. P., On the existence of Hermitian positive definite solutions of the matrix equation X^s + A^*X^−tA = Q, Linear Algebra and Its Applications. (2008) 429, no. 4, 673–687, https://doi.org/10.1016/j.laa.2008.03.019, 2428122, ZBL1143.15011.
10.1016/j.laa.2008.03.019
Web of Science® Google Scholar
15 Duan X. F. and Liao A. P., On the nonlinear matrix equation X + A^*X^−qA = Q(q ≥ 1), Mathematical and Computer Modelling. (2009) 49, no. 5-6, 936–945, https://doi.org/10.1016/j.mcm.2008.10.009, 2495010, ZBL1165.15302.
10.1016/j.mcm.2008.10.009
Google Scholar
16 Duan X. F. and Liao A. P., On Hermitian positive definite solution of the matrix equation , Journal of Computational and Applied Mathematics. (2009) 229, no. 1, 27–36, https://doi.org/10.1016/j.cam.2008.10.018, 2522496, ZBL1170.15005.
10.1016/j.cam.2008.10.018
Web of Science® Google Scholar
17 Duan X. F., Li C. M., and Liao A. P., Solutions and perturbation analysis for the nonlinear matrix equation , Applied Mathematics and Computation. (2011) 218, no. 8, 4458–4466, https://doi.org/10.1016/j.amc.2011.10.026.
10.1016/j.amc.2011.10.026
Web of Science® Google Scholar
18 Ding F., Liu P. X., and Ding J., Iterative solutions of the generalized Sylvester matrix equations by using the hierarchical identification principle, Applied Mathematics and Computation. (2008) 197, no. 1, 41–50, https://doi.org/10.1016/j.amc.2007.07.040, 2396289, ZBL1143.65035.
10.1016/j.amc.2007.07.040
Web of Science® Google Scholar
19 Ding F. and Chen T., Iterative least-squares solutions of coupled Sylvester matrix equations, Systems & Control Letters. (2005) 54, no. 2, 95–107, https://doi.org/10.1016/j.sysconle.2004.06.008, 2109576, ZBL1129.65306.
10.1016/j.sysconle.2004.06.008
Web of Science® Google Scholar
20 Ding F. and Chen T., Hierarchical gradient-based identification of multivariable discrete-time systems, Automatica. (2005) 41, no. 2, 315–325, https://doi.org/10.1016/j.automatica.2004.10.010, 2157667, ZBL1073.93012.
10.1016/j.automatica.2004.10.010
Web of Science® Google Scholar
21 Wang M. H., Wei M. S., and Hu S. H., An iterative method for the least-squares minimum-norm symmetric solution, CMES: Computer Modeling in Engineering & Sciences. (2011) 77, no. 3-4, 173–182, 2895803.
Web of Science® Google Scholar
22 Dehghan M. and Hajarian M., An iterative algorithm for the reflexive solutions of the generalized coupled Sylvester matrix equations and its optimal approximation, Applied Mathematics and Computation. (2008) 202, no. 2, 571–588, https://doi.org/10.1016/j.amc.2008.02.035, 2435692, ZBL1154.65023.
10.1016/j.amc.2008.02.035
Web of Science® Google Scholar
23 Dehghan M. and Hajarian M., Finite iterative algorithms for the reflexive and anti-reflexive solutions of the matrix equation A₁X₁B₁ + A₂X₂B₂ = C, Mathematical and Computer Modelling. (2009) 49, no. 9-10, 1937–1959, https://doi.org/10.1016/j.mcm.2008.12.014, 2532100, ZBL1171.15310.
10.1016/j.mcm.2008.12.014
Web of Science® Google Scholar
24 Hajarian M. and Dehghan M., Solving the generalized Sylvester matrix equation over reflexive and anti-reflexive matrices, International Journal of Control and Automation. (2011) 9, no. 1, 118–124, https://doi.org/10.1007/s12555-011-0115-5.
10.1007/s12555-011-0115-5
Google Scholar
25 Dehghan M. and Hajarian M., An iterative algorithm for solving a pair of matrix equations AYB = E, CYD = F over generalized centro-symmetric matrices, Computers & Mathematics with Applications. (2008) 56, no. 12, 3246–3260, https://doi.org/10.1016/j.camwa.2008.07.031, 2474579, ZBL1165.15301.
10.1016/j.camwa.2008.07.031
Web of Science® Google Scholar
26 Dehghan M. and Hajarian M., Analysis of an iterative algorithm to solve the generalized coupled Sylvester matrix equations, Applied Mathematical Modelling. (2011) 35, no. 7, 3285–3300, https://doi.org/10.1016/j.apm.2011.01.022, 2785279, ZBL1227.65037.
10.1016/j.apm.2011.01.022
Web of Science® Google Scholar
27 Dehghan M. and Hajarian M., The general coupled matrix equations over generalized bisymmetric matrices, Linear Algebra and Its Applications. (2010) 432, no. 6, 1531–1552, https://doi.org/10.1016/j.laa.2009.11.014, 2580446, ZBL1187.65042.
10.1016/j.laa.2009.11.014
Web of Science® Google Scholar
28 Dehghan M. and Hajarian M., An iterative method for solving the generalized coupled Sylvester matrix equations over generalized bisymmetric matrices, Applied Mathematical Modelling. (2010) 34, no. 3, 639–654, https://doi.org/10.1016/j.apm.2009.06.018, 2563346, ZBL1185.65054.
10.1016/j.apm.2009.06.018
Web of Science® Google Scholar
29 Wu A. G., Li B., Zhang Y., and Duan G. R., Finite iterative solutions to coupled Sylvester-conjugate matrix equations, Applied Mathematical Modelling. (2011) 35, no. 3, 1065–1080, https://doi.org/10.1016/j.apm.2010.07.053, 2740850, ZBL1211.15024.
10.1016/j.apm.2010.07.053
Web of Science® Google Scholar
30 Wu A. G., Lv L. L., and Duan G. R., Iterative algorithms for solving a class of complex conjugate and transpose matrix equations, Applied Mathematics and Computation. (2011) 217, no. 21, 8343–8353, https://doi.org/10.1016/j.amc.2011.02.113, 2802243, ZBL1222.65041.
10.1016/j.amc.2011.02.113
Web of Science® Google Scholar
31 Wu A. G., Lv L. L., and Hou M. Z., Finite iterative algorithms for extended Sylvester-conjugate matrix equations, Mathematical and Computer Modelling. (2011) 54, no. 9-10, 2363–2384, https://doi.org/10.1016/j.mcm.2011.05.045, 2834638, ZBL1235.65040.
10.1016/j.mcm.2011.05.045
Google Scholar
32 Bihan N. L. and Mars J., Singular value decomposition of matrices of Quaternions matrices: a new tool for vector-sensor signal processing, Signal Process. (2004) 84, no. 7, 1177–1199, https://doi.org/10.1016/j.sigpro.2004.04.001.
10.1016/j.sigpro.2004.04.001
Web of Science® Google Scholar
33 Bihan N. L. and Sangwine S. J., Jacobi method for quaternion matrix singular value decomposition, Applied Mathematics and Computation. (2007) 187, no. 2, 1265–1271, https://doi.org/10.1016/j.amc.2006.09.055, 2321330, ZBL1114.65321.
10.1016/j.amc.2006.09.055
Web of Science® Google Scholar
34 Farid F. O., Wang Q. W., and Zhang F., On the eigenvalues of quaternion matrices, Linear and Multilinear Algebra. (2011) 59, no. 4, 451–473, https://doi.org/10.1080/03081081003739204, 2802526, ZBL1237.15016.
10.1080/03081081003739204
Web of Science® Google Scholar
35 de Leo S. and Scolarici G., Right eigenvalue equation in quaternionic quantum mechanics, Journal of Physics A. (2000) 33, no. 15, 2971–2995, https://doi.org/10.1088/0305-4470/33/15/306, 1766502, ZBL0954.81008.
10.1088/0305-4470/33/15/306
Google Scholar
36 Sangwine S. J. and Bihan N. L., Quaternion singular value decomposition based on bidiagonalization to a real or complex matrix using quaternion Householder transformations, Applied Mathematics and Computation. (2006) 182, no. 1, 727–738, https://doi.org/10.1016/j.amc.2006.04.032, 2292081, ZBL1109.65037.
10.1016/j.amc.2006.04.032
Web of Science® Google Scholar
37 Took C. C., Mandic D. P., and Zhang F., On the unitary diagonalisation of a special class of quaternion matrices, Applied Mathematics Letters. (2011) 24, no. 11, 1806–1809, https://doi.org/10.1016/j.aml.2011.04.038, 2812216.
10.1016/j.aml.2011.04.038
Web of Science® Google Scholar
38 Wang Q. W., Chang H. X., and Ning Q., The common solution to six quaternion matrix equations with applications, Applied Mathematics and Computation. (2008) 198, no. 1, 209–226, https://doi.org/10.1016/j.amc.2007.08.091, 2403943, ZBL1141.15016.
10.1016/j.amc.2007.08.091
CAS Web of Science® Google Scholar
39 Wang Q. W., van der Woude J. W., and Chang H. X., A system of real quaternion matrix equations with applications, Linear Algebra and Its Applications. (2009) 431, no. 12, 2291–2303, https://doi.org/10.1016/j.laa.2009.02.010, 2563022, ZBL1180.15019.
10.1016/j.laa.2009.02.010
Web of Science® Google Scholar
40 Wang Q. W., Yu S. W., and Xie W., Extreme ranks of real matrices in solution of the quaternion matrix equation AXB = C with applications, Algebra Colloquium. (2010) 17, no. 2, 345–360, 2654356, ZBL1188.15016.
10.1142/S1005386710000349
Web of Science® Google Scholar
41 Wang Q. W. and Jiang J., Extreme ranks of (skew-)Hermitian solutions to a quaternion matrix equation, Electronic Journal of Linear Algebra. (2010) 20, 552–573, 2735973, ZBL1207.15016.
10.13001/1081-3810.1393
Web of Science® Google Scholar
42 Wang Q. W., Liu X., and Yu S. W., The common bisymmetric nonnegative definite solutions with extreme ranks and inertias to a pair of matrix equations, Applied Mathematics and Computation. (2011) 218, no. 6, 2761–2771, https://doi.org/10.1016/j.amc.2011.08.018, 2838182.
10.1016/j.amc.2011.08.018
Google Scholar
43 Wang Q. W., Zhou Y., and Zhang Q., Ranks of the common solution to six quaternion matrix equations, Acta Mathematicae Applicatae Sinica (English Series). (2011) 27, no. 3, 443–462, https://doi.org/10.1007/s10255-011-0083-9, 2810515.
10.1007/s10255-011-0083-9
CAS Web of Science® Google Scholar
44 Zhang F., Geršgorin type theorems for quaternionic matrices, Linear Algebra and Its Applications. (2007) 424, no. 1, 139–153, https://doi.org/10.1016/j.laa.2006.08.004, 2324381, ZBL1117.15017.
10.1016/j.laa.2006.08.004
Web of Science® Google Scholar
45 Zhang F., Quaternions and matrices of quaternions, Linear Algebra and Its Applications. (1997) 251, 21–57, https://doi.org/10.1016/0024-3795(95)00543-9, 1421264, ZBL0873.15008.
10.1016/0024-3795(95)00543-9
Web of Science® Google Scholar
46 Horn R. A. and Johnson C. R., Topics in Matrix Analysis, 1991, Cambridge University Press, Cambridge, UK, https://doi.org/10.1017/CBO9780511840371, 1091716.
10.1017/CBO9780511840371
Google Scholar
47 Peng Y. X., Hu X. Y., and Zhang L., An iteration method for the symmetric solutions and the optimal approximation solution of the matrix equation AXB = C, Applied Mathematics and Computation. (2005) 160, no. 3, 763–777, https://doi.org/10.1016/j.amc.2003.11.030, 2113117, ZBL1068.65056.
10.1016/j.amc.2003.11.030
Web of Science® Google Scholar

Citing Literature

All articles

An Efficient Algorithm for the Reflexive Solution of the Quaternion Matrix Equation AXB + CX^HD = F

Abstract

1. Introduction

2. Preliminary

3. Main Results

3.1. The Solution of Problem 1

3.2. The Solution of Problem 2

4. Examples

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

An Efficient Algorithm for the Reflexive Solution of the Quaternion Matrix Equation AXB + CXHD = F

Abstract

1. Introduction

2. Preliminary

3. Main Results

3.1. The Solution of Problem 1

3.2. The Solution of Problem 2

4. Examples

5. Conclusions

Acknowledgments

References

Citing Literature

Figures

References

Related

Information

An Efficient Algorithm for the Reflexive Solution of the Quaternion Matrix Equation AXB + CX^HD = F