Volume 2013, Issue 1 196139

Research Article

Open Access

Existence and Global Exponential Stability of Equilibrium for Impulsive Cellular Neural Network Models with Piecewise Alternately Advanced and Retarded Argument

Corresponding Author

Kuo-Shou Chiu

[email protected]

orcid.org/0000-0002-3823-5898

Departamento de Matemática, Facultad de Ciencias Básicas, Universidad Metropolitana de Ciencias de la Educación, José Pedro Alessandri 774, Santiago, Chile umce.cl

Search for more papers by this author

Kuo-Shou Chiu,

Corresponding Author

Kuo-Shou Chiu

[email protected]

orcid.org/0000-0002-3823-5898

Departamento de Matemática, Facultad de Ciencias Básicas, Universidad Metropolitana de Ciencias de la Educación, José Pedro Alessandri 774, Santiago, Chile umce.cl

Search for more papers by this author

First published: 31 December 2013

https://doi.org/10.1155/2013/196139

Citations: 14

Academic Editor: Agacik Zafer

Share a link

Email
Wechat
Bluesky

Abstract

We introduce impulsive cellular neural network models with piecewise alternately advanced and retarded argument (in short IDEPCA). The model with the advanced argument is system with strong anticipation. Some sufficient conditions are established for the existence and global exponential stability of a unique equilibrium. The approaches are based on employing Banach’s fixed point theorem and a new IDEPCA integral inequality of Gronwall type. The criteria given are easily verifiable, possess many adjustable parameters, and depend on impulses and piecewise constant argument deviations, which provides exibility for the design and analysis of cellular neural network models. Several numerical examples and simulations are also given to show the feasibility and effectiveness of our results.

1. Introduction

Chua and Yang [1] proposed a novel class of information-processing systems called cellular neural networks (CNNs) in 1988. Like neural networks, it is a large-scale nonlinear analog circuit which processes signals in real time. Like cellular automata [2] it is made of a massive aggregate of regularly spaced circuit clones, called cells, which communicate with each other directly only through its nearest neighbors. Each cell is made of a linear capacitor, a nonlinear voltage-controlled current source, and a few resistive linear circuit elements. The key features of neural networks are asynchronous parallel processing and global interaction of network elements. Impressive applications of neural networks have been proposed for various fields such as optimization, linear and nonlinear programming, associative memory, pattern recognition, and computer vision. For the circuit diagram and connection pattern implementing the CNN, one can refer to [1]. The CNN can be applied in signal processing and can also be used to solve some image processing and pattern recognition problems [3]. However, it is necessary to solve some dynamic image processing and pattern recognition problems by using delayed cellular neural networks (DCNN) [4–6]. The study of the stability of CNN and DCNN is known to be an important problem in theory and applications.

On the other hand, in real world, many evolutionary processes are characterized by abrupt changes at certain time. These changes are known to be impulsive phenomena, which are included in many fields such as physics, chemistry, population dynamics, and optimal control. Fundamental theory of impulsive differential equations has been developed in [7]. Furthermore, researches of impulsive differential equations have been received much interesting in recent years [8–18]. Meanwhile, several kinds of neural networks with impulse have been investigated. In particular, Xu and Yang established the delay differential inequalities with impulsive initial conditions; some new sufficient conditions for global exponential stability of impulsive delay model were obtained [15, 16].

Most neural networks can be classified into two types, continuous or discrete. However, many real-world systems and natural processes cannot be categorized into one of them. They display characteristics both continuous and discrete styles. For instance, some biological neural networks in biology, bursting rhythm models in pathology, and optimal control models in economics are characterized by abrupt changes of state. These are the familiar impulsive phenomena.

It is well known that applications of CNN depend crucially on the dynamical behavior of the networks. In these applications, stability and convergence of neural networks are prerequisites. However, in the design of neural networks one is interested not only in the uniform asymptotic stability but also in the global exponential stability, which guarantees a neural network to converge fast enough in order to achieve fast response. In addition, in the analysis of dynamical neural networks for parallel computation and optimization, to increase the rate of convergence to the equilibrium point of the networks and reduce the neural computing time, it is necessary to ensure a desired exponential convergence rate of the networks′ trajectories, starting from arbitrary initial states to the equilibrium point which corresponds to the optimal solution. Thus, from the mathematical and engineering points of view, it is required that the neural networks have a unique equilibrium point which is globally exponentially stable. Therefore, the problem of stability analysis has received great attention and many results on this topic have been reported in the literature. See, for instance, [4, 9, 13, 19–27] and references cited therein.

1.1. Piecewise Constant Impulsive Systems

Differential equations with piecewise constant argument (in short DEPCA) are first considered by Shah and Wiener [28] and Cooke and Wiener [29] in the 80s and have been developed by many authors. Applications of DEPCAs are discussed in [30]. Theory and practice of DEPCA of general type, have been discussed extensively in [31–37]. Piecewise constant systems exist in widely expanded areas such as biomedicine, chemistry, mechanical engineering, and physics. The systematical studies with mathematical models involving piecewise constant arguments were initiated for solving some biomedical problems. These kinds of equations are similar in structure to those found in certain sequential-continuous models of disease dynamics. In [38], the following system of equations describing the dynamics of the disease for generation n = 1,2, … is investigated:

()

while

()

where c is the death rate and k is the horizontal transmission factor. These types of models are special cases of the general form

()

which arise naturally in a number of models of epidemic. DEPCAs usually describe hybrid dynamical systems (a combination of continuous and discrete) and so combine properties of both differential and difference equations.

Impulsive differential equations with discontinuous argument are proposed as an open problem by Wiener [30] in 1994, namely, the impulsive differential equations with piecewise constant argument: IDEPCA. As we know, impulsive differential equations with piecewise constant arguments (in short IDEPCA) are studied in a few papers [8, 39, 40].

1.2. Model Description

First, let us give a general description of the mathematical model of ICNNs with piecewise alternately advanced and retarded argument:

()

where [·] signifies the greatest integer function, l and m are positive real numbers such that l < m, t, x_i ∈ ℝ⁺, i = 1,2, …, n, Δx_i(mk − l) = x_i(mk − l) − x_i(mk − l⁻), and x_i(mk − l⁻) =

. Moreover, n denotes the number of neurons in the network, x_i(t) corresponds to the state of the ith unit at time t, f_j(x_j(t)) and g_j(x_j(m[(t + l)/m])) denote, respectively, the measures of activation to its incoming potentials of the unit j at time t and discrete-time m[(t + l)/m], a_i denotes the rate with which the unit i resets its potential to the resting state when isolated from other units and inputs, b_ij denotes the synaptic connection weight of the unit j on the unit i at time t, c_ij denotes the synaptic connection weight of the unit j on the unit i at discrete-time m[(t + l)/m], and d_i is the input from outside the network to the unit i. The numbers x_i(mk − l⁻) and x_i(mk − l) are, respectively, the states of the ith unit before and after impulse perturbation at the moment mk − l, k ∈ ℕ, and represent the abrupt change of the state J_ik(x_i(mk − l⁻)) at the impulsive moment mk − l.

Let us clarify why the IDEPCA (4a)-(4b) is of alternately advanced and retarded type; that is, the argument can change its deviation character during the motion. The argument is deviated if it is advanced or retarded. Fix k ∈ ℕ, and consider the IDEPCA on the interval I_k = [mk − l, m(k + 1) − l). Then, the identification function m[(t + l)/m] is equal to mk. If , then m[(t + l)/m] ≥ t and IDEPCA (4a)-(4b) is an equation with advanced argument. Similarly, if then m[(t + l)/m] < t and IDEPCA (4a)-(4b) is an equation with retarded argument. Consequently, IDEPCA (4a)-(4b) changes the type of deviation of the argument during the process. In other words, the IDEPCA (4a)-(4b) is of alternately advanced and retarded type.

For any solution x(t) = (x₁(t), …, x_n(t)) ^T of IDEPCA (4a)-(4b), the model can be summarized as follows:

()

where A = diag (a₁, …, a_n), B = (b_ij) _n×n, and C = (c_ij) _n×n are constant matrices and D = (d₁, …, d_n) is a constant vector. Moreover, the functions f : ℝⁿ ↦ ℝⁿ, g : ℝⁿ ↦ ℝⁿ satisfy (∂f_i/∂x_j) = (∂g_i/∂x_j) = 0 when i ≠ j.

To the best of our knowledge, cellular neural network with piecewise constant argument has been developed by few authors, for example, Huang et al. Reference [41] considered first the following cellular neural network with piecewise constant delay:

()

where [·] signifies the greatest integer function. Some sufficient conditions of existence and attractivity of almost periodic sequence solution were given for the corresponding discrete-time analogue:

()

In 2010, Akhmet and Yılmaz [8] considered first the following impulsive neural network with only piecewise constant retarded argument:

()

where β(t) = θ_k if θ_k < t < θ_k+1, k ∈ ℕ, t ∈ ℝ⁺, is an identification function and θ_k > 0, k ∈ ℕ, is a sequence of real numbers. Several sufficient conditions are obtained for the existence and stability of a unique ω-periodic solution.

In this paper, we for the first time study the dynamic behavior of impulsive cellular neural network models that combine the properties of impulsive differential equations and discrete-time difference equations, that is, the following impulsive cellular neural network with piecewise alternately advanced and retarded argument:

()

The purpose of this paper is to derive some new and simple sufficient conditions for the existence and uniqueness of solutions of the ICNNs with IDEPCA system (5a)-(5b), which is globally exponentially stable. This paper is organized as follows. In Section 2, we establish several criteria for the existence and uniqueness of a unique equilibrium of the ICNNs with IDEPCA system and the equivalence lemma for (5a)-(5b). Here, a new IDEPCA Gronwall-type inequality is very useful. In Section 3, we derive some sufficient conditions which ensure that a unique equilibrium of the ICNNs with IDEPCA system (5a)-(5b) is globally exponentially stable. In Section 4, two illustrative examples and the numerical simulations are given to demonstrate the effectiveness of our results. The conclusions are drawn in Section 5.

2. Existence and Uniqueness Theorems

In this section, sufficient conditions that govern the network parameters and the activation functions are established for the existence of a unique equilibrium state of the impulsive cellular neural network models (5a)-(5b).

2.1. Preliminaries and Definition

In this section, we will focus our attention on some preliminary results which will be used in the existence and uniqueness of solutions of the ICNNs with IDEPCA system (5a)-(5b).

For every t ∈ ℝ, let i = i(t) ∈ ℕ be the unique integer such that t ∈ I_i = [mi − l, m(i + 1) − l).

For the sake of convenience, two of the standing assumptions are formulated below.

Lipschitz Condition

(L)
The activation functions f_j and g_j with f_j(0) = 0, g_j(0) = 0 (j = 1,2, …, n) satisfy the Lipschitz condition; that is, there are constants , such that
()
for all u, v ∈ ℝ⁺.

The impulsive operator J_k satisfies

()

for all u, v ∈ ℝ⁺, j = 1, …, n, k ∈ ℕ, where

is a positive Lipschitz constant.

Existence condition

(E)
Consider
()
where .

First, we prove the existence and uniqueness of solutions of IDEPCA system (5a)-(5b). A natural extension of the original definition of a solution of DEPCA [28–30, 42] allows us to define a solution of IDEPCA system.

Definition 1. A function x is a solution of IDEPCA system (5a)-(5b) in ℝ⁺ = [0, ∞) if

(i)
x(t) is continuous for t ∈ ℝ⁺ with the possible exception of the points t = mk − l, k ∈ ℕ,
(ii)
x(t) is right continuous and has left-hand limits at the points t = mk − l, k ∈ ℕ,
(iii)
x(t) is differentiable and satisfies (5a) for any t ∈ ℝ⁺, with the possible exception of the points t = mk − l, k ∈ ℕ, where one-sided derivatives exist,
(iv)
x(n) satisfies (5b) for n = km − l, k ∈ ℕ.

To study nonlinear IDEPCA system, we will use the approach based on the construction of an equivalent integral equation. Let us give the following proposition.

Proposition 2. Let (τ, x₀) ∈ ℝ⁺ × ℝⁿ. The function x(t) = x(t, τ, x₀) is a solution on ℝ⁺ of the IDEPCA system (5a)-(5b) in the sense of Definition 1 if and only if it is a solution of the integral equation

()

In particular, one has the following integral equations: for i = 1, …, n, t ∈ ℝ⁺,

()

The proof of Proposition 2 is almost identical to the verification in [7] with slight changes which are caused by the piecewise constant argument.

In the next, we give the following lemma about IDEPCA integral inequality of Gronwall type, which is one of the most important auxiliary results of the present paper.

Lemma 3. Let u : ℝ → [0, ∞) be a function such that u is continuous with possible points of discontinuity of the first kind at t = mk − l,k ∈ ℕ, and η₁, η₂ are nonnegative real constants satisfying

()

Suppose that for t ≥ τ the inequality

()

holds. Then for t ≥ τ,

()

Proof. Call v(t) the right member of (16). So v(τ) = u(τ), u ≤ v, and v is a piecewise differentiable and nondecreasing function and, by (16), it satisfies

()

k ∈ ℕ and for any t ≥ r with t,r ∈ I_i

()

With t = mi and r = mi − l in (21) for t ∈ I_i, since v is a nondecreasing function, we get

()

Considering the particular case τ = t_i and taking v(t_i) = u(t_i) and u ≤ v, by (15) and (22), estimate (19) follows. Take now in (21) t ∈ I_i and r = mi − l to obtain

()

because v is a nondecreasing function. Now, we can apply the classical Gronwall’s Lemma to get

()

By the impulsive effect (20), we have

()

From (25), recursively we obtain

()

using v(τ) = u(τ) and (19); then we give (17) and (18). The proof is complete. This IDEPCA inequality of Gronwall type seems to be new.

We need to have the global unique existence of solutions x(t) = x(t, τ, x₀) on ℝ⁺ of the nonlinear IDEPCA system (5a)-(5b).

One can easily see that IDEPCA system (5a)-(5b) has the form of DEPCA system without impulsive effect within the intervals [mi − l, m(i + 1) − l),i ∈ ℕ; then using the same technique of [34, 35, 37] we have the following results.

Proposition 4. Suppose that conditions (L) and (E) hold. For any (τ, x₀) ∈ ℝ⁺ × ℝⁿ there exists a unique solution x(t) = x(t, τ, x₀) of the IDEPCA system (5a)-(5b) on [mi(τ) − l, m(i(τ) + 1) − l).

Theorem 5. Under conditions (L) and (E), for every (τ, x₀) ∈ ℝ⁺ × ℝⁿ, there exists a unique solution x(t) = x(t, τ, x₀) of the IDEPCA system (5a)-(5b) with x(τ) = x₀ for t ∈ [τ, ∞) in the sense of Definition 1.

Proof. Fix τ ∈ ℝ⁺; then τ ∈ I_i(τ) = [mi(τ) − l, mi(τ) + m − l). Use Proposition 4 with x(τ) = x₀ to obtain the unique solution x(t) = x(t, τ, x₀) on I_i(τ). Then apply the impulse condition to evaluate uniquely

()

Next, on the interval I_i(τ)+1 = [mi(τ) + m − l, mi(τ) + 2m − l) the solution satisfies the DEPCA:

()

The IDEPCA system has a unique solution y(t, mi(τ) + m − l, x(mi(τ) + m − l, τ, x₀)). By definition of the solution of IDEPCA system (5a)-(5b), x(t, τ, x₀) = y(t, mi(τ) + m − l, x(mi(τ) + m − l, τ, x₀)) on I_i(τ)+1 = [mi(τ) + m − l, mi(τ) + 2m − l). The mathematical induction completes the proof.

2.2. Existence and Uniqueness of Equilibrium

When impulsive cellular neural network models are used for the solution of optimization problems, one of the fundamental issues in the design of a network is concerned with the existence of a unique globally exponentially stable equilibrium state of network (5a)-(5b). Without requiring the boundedness, differentiability, or monotonicity, we establish easily verifiable sufficient conditions for the existence of a unique equilibrium state in this section.

Let us denote an equilibrium state of the impulsive cellular neural network models (5a)-(5b) by the constant vector

, where each

is governed by the algebraic system

()

Here, it is assumed that the impulse functions J_ik(·) satisfy

for all i = 1, …, n, k ∈ ℕ.

In the following theorem, we obtain sufficient conditions for the existence of a unique equilibrium, , of the impulsive cellular neural network models (5a)-(5b).

Theorem 6. Suppose that conditions (L) and (E) hold and the neural parameters a_i, b_ij, and c_ij and Lipschitz constants , satisfy

()

Then there exists a unique equilibrium state x^* of the ICNNs with IDEPCA system (5a)-(5b).

Proof. Let us consider a mapping G(u) = (G₁(u), G₂(u), …, G_n(u)) ^T ∈ ℝⁿ, where u = (u₁, u₂, …, u_n) ^T ∈ ℝⁿ and

()

By applying the hypotheses,

()

where the number

()

satisfies 0 < ρ < 1 by virtue of condition (30). Thus,

()

for any two vectors u, v ∈ ℝⁿ implying that the mapping G : ℝⁿ → ℝⁿ is a global contraction on ℝⁿ endowed with the supremum norm. Hence, there is a unique fixed point x^* ∈ ℝⁿ that satisfies G(x^*) = x^* (i.e.,

for i = 1, …, n). This point defines the unique equilibrium state of the impulsive cellular neural network models (5a)-(5b). The proof is now complete.

3. Global Exponential Stability of Equilibrium

The existence and stability of a unique equilibrium state are usually a requirement in the design of cellular neural network models for various applications, particularly when there are destabilizing agents such as retarded arguments and impulses. However, even if the unique stable state exists, these agents may affect the convergence speed of the network, which in turn can downgrade the performance of the network in applications that demand fast computation in real-time mode. Thus, exponential stability is usually desirable for an impulsive network, and sufficient conditions for the global exponential stability of the unique equilibrium state x^* of the ICNNs with IDEPCA system (5a)-(5b) are obtained in this section.

For analytical convenience, the ICNNs with IDEPCA system (5a)-(5b) can be simplified as follows. Let

()

so that the ICNNs with IDEPCA system (5a)-(5b) can be written as

()

where

and

The activation functions

, inheriting the properties of f_i(·), satisfy

()

the functions

inherit the properties of g_i(·), namely,

()

and the impulsive operator

satisfies

()

for all u, v ∈ ℝ⁺, i = 1, …, n, k ∈ ℕ.

It is clear that the stability of the zero solution of (36) is equivalent to that of the equilibrium x^* of the ICNNs with IDEPCA system (4a)-(4b). Therefore, we restrict our discussion to the stability of the zero solution of (36).

First of all, we give the following definition and lemma, which will be used in the proof of the stability of the zero solution for the ICNNs with IDEPCA system.

Definition 7. The equilibrium x^* of the ICNNs with IDEPCA system (5a)-(5b) is said to be globally exponentially stable if there exist positive constants α and λ such that the estimation

()

is valid for all t ≥ τ.

Lemma 8. If (L) and (E) are satisfied, then the solutions φ and ψ of the IDEPCA system (5a)-(5b) satisfy for all t ≥ τ the inequality

()

where λ_i(t) = a_* − β^* − ℒ_i(t),

()

Proof. Suppose that φ(t) = (φ₁, …, φ_n) ^T and ψ(t) = (ψ₁, …, ψ_n) ^T are arbitrary solutions of the IDEPCA system (5a)-(5b). Let y(t) = φ(t) − ψ(t) and by (5a) and (5b) it follows that y(·) satisfies

()

By the variation of parameters formula, it can be proved that

()

where

()

Notice that (L) implies that

()

By (44), we can deduce that v_i(t) = exp (a_* · (t − τ)) | y_i(t)| satisfies

()

for any finite t ∈ [τ, ∞).

Hence, by Lemma 3 of IDEPCA Gronwall′s inequality implies

()

Then, we have

()

and the statement (41) follows.

The following result will show sufficient conditions for the global exponential stability of the unique equilibrium of the ICNNs with IDEPCA system (5a)-(5b).

Theorem 9. If the assumptions of Theorem 6, (42) and

()

are satisfied, then the unique equilibrium x^* of the ICNNs with IDEPCA system (5a)-(5b) is globally exponentially stable.

Proof. By Theorem 6, we know that the IDEPCA system (5a)-(5b) has a unique equilibrium x^*. Let x(t, x₀) be an arbitrary solution of (5a)-(5b) with initial condition x₀ and define z(t) = x(t, x₀) − x^*. By Lemma 8 and (42), we obtain

()

where λ_i(t) = a_* − β^* − ℒ_i(t). So, using (52), we see that |z(t)| → 0 as t → ∞. That is, the zero solution of ICNNs with IDEPCA system (36) is globally exponentially stable. Therefore, the unique equilibrium x^* of the ICNNs with IDEPCA system (5a)-(5b) is globally exponentially stable.

Remark 10. To the best of the author′s knowledge, this is the first time we investigate impulsive cellular neural network models with piecewise alternately advanced and retarded argument in equilibrium case. Sufficient conditions are gained for the existence and exponential stability of a unique equilibrium of the ICNNs with IDEPCA system. And our results can be extended to a unique equilibrium of the CNNs with DEPCA system. See Corollaries 11–12. Our results about exponential stability of a unique equilibrium of the ICNNs with IDEPCA system may give some insight into the application of neural networks.

As immediate corollaries of Lemma 8 and Theorem 9, the following results without impulsive effects are true.

Corollary 11. If (L) and (E) are satisfied, then the solutions φ and ψ of the DEPCA system (5a) satisfy for all t ≥ τ the inequality

()

where λ = a_* − β^*,

()

Corollary 12. If the assumptions of Corollary 11 and

()

are satisfied, then the unique equilibrium x^* of the CNNs with DEPCA system (5a) is globally exponentially stable.

Remark 13. In [41], authors investigated discrete-time cellular neural network without impulsive effects in almost periodic case. Simple sufficient conditions are gained for a unique almost periodic sequence solution which is globally attractive. When m = 1, l = 0, this conclusion of Corollary 12 cannot be derived by applying the corresponding stability result for cellular neural networks given in the literature [41] with a_i, b_ij, c_ij, and d_i being constant coefficients.

4. Examples and Simulations

In this section, we give two examples with numerical simulations to illustrate the effectiveness of the proposed method and results.

Example 1. Consider the following impulsive cellular neural networks with piecewise alternately advanced and retarded argument:

()

where

. One can check that the point

satisfies the algebraic system

()

approximately. And it is clear that

for i = 1,2. By simple calculation, we can see that a_* = 0.9,

, and

. Then

()

By Theorem 6, we know that the ICNNs with IDEPCA system (57) have a unique equilibrium state x^*, approximately with the error, which is less than 10⁻¹¹ (evaluated by MATLAB).

Moreover, we have

()

Thus, according to Theorem 9, the ICNNs with IDEPCA system (57) have a unique globally exponentially stable equilibrium. The numerical simulations, showing the convergence of the unique equilibrium x^* of the ICNNs with and without impulses (57), are given in Figures 1(a) and 1(b).

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

(a) The simulation, where the initial value is chosen as (1,3) ^T, illustrates that all trajectories uniformly converge to the unique equilibrium x^* = (1.943,1.57) ^T for the ICNNs (57) with impulsive effects. (b) The simulation, where the initial value is chosen as (1,3) ^T, illustrates that all trajectories uniformly converge to the unique equilibrium x^* = (1.943,1.57) ^T for the ICNNs (57) without impulsive effects.

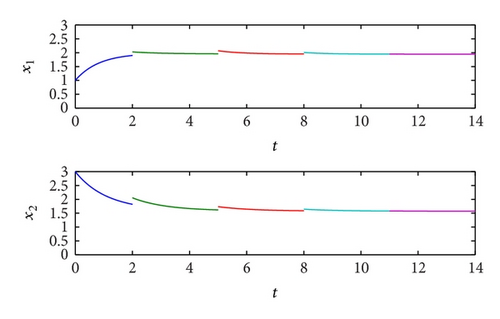
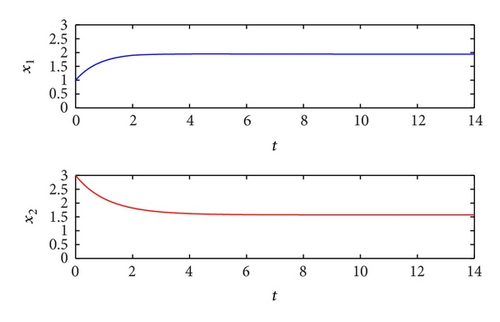
Example 2. Consider the following impulsive cellular neural networks model with piecewise constant argument:

()

where

. One can check that the point

satisfies the algebraic system (29) approximately and it is clear that

for i = 1,2. The output functions are f₁(x₁) = tanh(x₁/3), f₂(x₂) = tanh(x₂/4), g₁(x₁) = (|x₁ + 1 | −|x₁ − 1|)/10, and g₂(x₂) = (|x₂ + 1 | −|x₂ − 1|)/8.

We can easily obtain that a_* = 0.8, , , , , and .

Then we give

()

By Theorem 6, we know that the ICNNs with IDEPCA system (61) have a unique equilibrium.

In addition, we have

()

From Theorem 9, the ICNNs with IDEPCA system (61) have the unique equilibrium x^* which is globally asymptotically stable and all other solutions of the IDEPCA system (61) converge exponentially to it as t → ∞. The numerical simulations, showing the convergence of the unique equilibrium x^* of the ICNNs with and without impulses (61), are given in Figures 2(a) and 2(b).

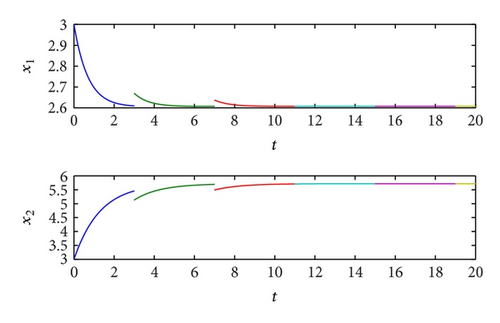
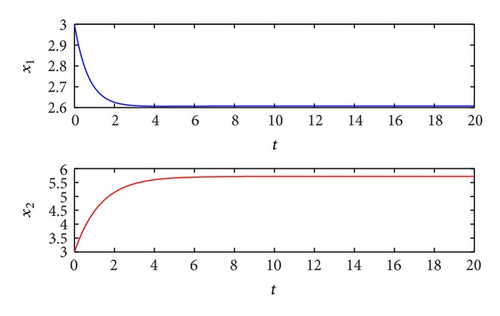
5. Conclusions

This is the first time that impulsive differential equations with alternately advanced and retarded argument have been applied to the model of cellular neural network models, and this paper has provided sufficient conditions guaranteeing the existence, uniqueness, and global exponential stability of the unique equilibrium of the impulsive cellular neural network models for the considered system based on a new IDEPCA integral inequality of Gronwall type and fixed point theorem. In addition, our method gives new ideas not only from the modeling point of view but also from that of theoretical opportunities since the impulsive cellular neural network model equation involves piecewise constant arguments of both advanced and delayed types. The obtained results could be useful in the design and applications of impulsive cellular neural network models. Furthermore, the examples with numerical simulations are given to show the effectiveness of the proposed method and results.

Acknowledgments

The author thanks the referees and editor very much for their valuable suggestions which made this paper much improved. This research was in part supported by FIBE 01-12 DIUMCE.

References

1 Chua L. O. and Yang L., Cellular neural networks: theory, IEEE Transactions on Circuits and Systems. (1988) 35, no. 10, 1257–1272, https://doi.org/10.1109/31.7600, MR960777, ZBL0663.94022.
10.1109/31.7600
Web of Science® Google Scholar
2 Wolfram S., Theory and Applications of Cellular Automata, 1986, 1, World Scientific, Singapore, Advanced Series on Complex Systems, MR857608.
Google Scholar
3 Chua L. O. and Yang L., Cellular neural networks: applications, IEEE Transactions on Circuits and Systems. (1988) 35, no. 10, 1273–1290, https://doi.org/10.1109/31.7601, MR960778.
10.1109/31.7601
Web of Science® Google Scholar
4 Civalleri P. P., Gilli M., and Pandolfi L., On stability of cellular neural networks with delay, IEEE Transactions on Circuits and Systems I. (1993) 40, no. 3, 157–165, https://doi.org/10.1109/81.222796, MR1232558, ZBL0792.68115.
10.1109/81.222796
Web of Science® Google Scholar
5 Cao J., A set of stability criteria for delayed cellular neural networks, IEEE Transactions on Circuits and Systems I. (2001) 48, no. 4, 494–498, https://doi.org/10.1109/81.917987, MR1827297, ZBL0994.82066.
10.1109/81.917987
Web of Science® Google Scholar
6 Chua L. O. and Roska T., Stability of a class of nonreciprocal cellular neural networks, IEEE Transactions on Circuits and Systems I. (1990) 37, no. 12, 1520–1527, https://doi.org/10.1109/31.101272.
10.1109/31.101272
Web of Science® Google Scholar
7 Lakshmikantham V., Bainov D. D., and Simeonov P. S., Theory of Impulsive Differential Equations, 1989, 6, World Scientific, Singapore, Series in Modern Applied Mathematics, MR1082551.
10.1142/0906
Google Scholar
8 Akhmet M. U. and Yılmaz E., Impulsive Hopfield-type neural network system with piecewise constant argument, Nonlinear Analysis: Real World Applications. (2010) 11, no. 4, 2584–2593, https://doi.org/10.1016/j.nonrwa.2009.09.003, MR2661925, ZBL1202.92001.
10.1016/j.nonrwa.2009.09.003
Web of Science® Google Scholar
9 Shao Y. F., Xu C. J., and Zhang Q. H., Globally exponential stability of periodic solutions to impulsive neural networks with time-varying delays, Abstract and Applied Analysis. (2012) 14, 358362, https://doi.org/10.1155/2012/358362, MR2922935, ZBL1242.93104.
10.1155/2012/358362
Google Scholar
10 Sun G. and Li X., A new criterion to global exponential stability for impulsive neural networks with continuously distributed delays, Mathematical Methods in the Applied Sciences. (2010) 33, no. 17, 2107–2117, https://doi.org/10.1002/mma.1322, MR2762322, ZBL1213.34085.
10.1002/mma.1322
Web of Science® Google Scholar
11 Wu B., Liu Y., and Lu J., New results on global exponential stability for impulsive cellular neural networks with any bounded time-varying delays, Mathematical and Computer Modelling. (2012) 55, no. 3-4, 837–843, https://doi.org/10.1016/j.mcm.2011.09.009, MR2887425, ZBL1255.93103.
10.1016/j.mcm.2011.09.009
PubMed Web of Science® Google Scholar
12 Xi Q., Global exponential stability for a class of generalized delayed neural networks with impulses, Mathematical Methods in the Applied Sciences. (2011) 34, no. 11, 1414–1420, https://doi.org/10.1002/mma.1451, MR2839383, ZBL1219.92002.
10.1002/mma.1451
Web of Science® Google Scholar
13 Xia Y. and Wong P. J. Y., Global exponential stability of a class of retarded impulsive differential equations with applications, Chaos, Solitons & Fractals. (2009) 39, no. 1, 440–453, https://doi.org/10.1016/j.chaos.2007.04.005, MR2504578, ZBL1197.34146.
10.1016/j.chaos.2007.04.005
Web of Science® Google Scholar
14 Xiang L., Dynamical analysis of impulsive neural networks with time-varying delays, Mathematical Methods in the Applied Sciences. (2012) 35, no. 13, 1564–1569, https://doi.org/10.1002/mma.2542, MR2957517, ZBL1253.34068.
10.1002/mma.2542
Web of Science® Google Scholar
15 Xu D. and Yang Z., Impulsive delay differential inequality and stability of neural networks, Journal of Mathematical Analysis and Applications. (2005) 305, no. 1, 107–120, https://doi.org/10.1016/j.jmaa.2004.10.040, MR2128115, ZBL1091.34046.
10.1016/j.jmaa.2004.10.040
Web of Science® Google Scholar
16 Yang Z. and Xu D., Impulsive effects on stability of Cohen-Grossberg neural networks with variable delays, Applied Mathematics and Computation. (2006) 177, no. 1, 63–78, https://doi.org/10.1016/j.amc.2005.10.032, MR2234497, ZBL1103.34067.
10.1016/j.amc.2005.10.032
Web of Science® Google Scholar
17 Zhang Q., Shao Y., and Liu J., Analysis of stability for impulsive fuzzy Cohen-Grossberg BAM neural networks with delays, Mathematical Methods in the Applied Sciences. (2013) 36, no. 7, 773–779, https://doi.org/10.1002/mma.2624, MR3056935, ZBL1271.34080.
10.1002/mma.2624
Web of Science® Google Scholar
18 Zhang Y., Robust exponential stability of discrete-time uncertain impulsive neural networks with time-varying delay, Mathematical Methods in the Applied Sciences. (2012) 35, no. 11, 1287–1299, https://doi.org/10.1002/mma.2531, MR2945852, ZBL1250.93099.
10.1002/mma.2531
Web of Science® Google Scholar
19 Barone E. and Tebaldi C., Stability of equilibria in a neural network model, Mathematical Methods in the Applied Sciences. (2000) 23, no. 13, 1179–1193, https://doi.org/10.1002/1099-1476(20000910)23:13<1179::AID-MMA158>3.3.CO;2-Y, MR1779387, ZBL0959.92002.
10.1002/1099-1476(20000910)23:13<1179::AID-MMA158>3.0.CO;2-6
Web of Science® Google Scholar
20 Cao J., Global asymptotic stability of neural networks with transmission delays, International Journal of Systems Science. (2000) 31, no. 10, 1313–1316, https://doi.org/10.1080/00207720050165807.
10.1080/00207720050165807
Web of Science® Google Scholar
21 Cao J., Yuan K., and Li H. X., Global asymptotical stability of recurrent neural networks with multiple discrete delays and distributed delays, IEEE Transactions on Neural Networks. (2006) 17, no. 6, 1646–1651, https://doi.org/10.1109/TNN.2006.881488.
10.1109/TNN.2006.881488
PubMed Web of Science® Google Scholar
22 Du Y., Xu R., and Liu Q., Stability and bifurcation analysis for a neural network model with discrete and distributed delays, Mathematical Methods in the Applied Sciences. (2013) 36, no. 1, 49–59, https://doi.org/10.1002/mma.2568, MR3008322, ZBL06133216.
10.1002/mma.2568
Web of Science® Google Scholar
23 Liu Q. S. and Cao J., Improved global exponential stability criteria of cellular neural networks with time-varying delays, Mathematical and Computer Modelling. (2006) 43, no. 3-4, 423–432, https://doi.org/10.1016/j.mcm.2005.11.007, MR2214652, ZBL1157.34055.
10.1016/j.mcm.2005.11.007
Google Scholar
24 Liu X. Z. and Dickson R., Stability analysis of Hopfield neural networks with uncertainty, Mathematical and Computer Modelling. (2001) 34, no. 3-4, 353–363, https://doi.org/10.1016/S0895-7177(01)00067-X, MR1835832, ZBL0999.34052.
10.1016/S0895-7177(01)00067-X
Google Scholar
25 Oliveira J. J., Global asymptotic stability for neural network models with distributed delays, Mathematical and Computer Modelling. (2009) 50, no. 1-2, 81–91, https://doi.org/10.1016/j.mcm.2009.02.002, MR2542590, ZBL1185.34107.
10.1016/j.mcm.2009.02.002
Google Scholar
26 Qiu J. and Cao J., Delay-dependent robust stability of neutral-type neural networks with time delays, Journal of Mathematical Control Science and Applications. (2007) 1, 179–188.
Google Scholar
27 Wei X., Zhou D., and Zhang Q., On asymptotic stability of discrete-time non-autonomous delayed Hopfield neural networks, Computers & Mathematics with Applications. (2009) 57, no. 11-12, 1938–1942, https://doi.org/10.1016/j.camwa.2008.10.031, MR2523361, ZBL1186.39028.
10.1016/j.camwa.2008.10.031
Web of Science® Google Scholar
28 Shah S. M. and Wiener J., Advanced differential equations with piecewise constant argument deviations, International Journal of Mathematics and Mathematical Sciences. (1983) 6, no. 4, 671–703, https://doi.org/10.1155/S0161171283000599, MR729389, ZBL0534.34067.
10.1155/S0161171283000599
Google Scholar
29 Cooke K. L. and Wiener J., Retarded differential equations with piecewise constant delays, Journal of Mathematical Analysis and Applications. (1984) 99, no. 1, 265–297, https://doi.org/10.1016/0022-247X(84)90248-8, MR732717, ZBL0557.34059.
10.1016/0022-247X(84)90248-8
Web of Science® Google Scholar
30 Wiener J., Generalized Solutions of Functional-Differential Equations, 1993, World Scientific, Singapore, MR1233560.
10.1142/1860
Google Scholar
31 Chiu K.-S. and Pinto M., Oscillatory and periodic solutions in alternately advanced and delayed differential equations, Carpathian Journal of Mathematics. (2013) 29, no. 2, 149–158.
10.37193/CJM.2013.02.15
Web of Science® Google Scholar
32 Chiu K.-S., Stability of oscillatory solutions of differential equations with a general piecewise constant argument, Electronic Journal of Qualitative Theory of Differential Equations. (2011) 88, 1–15, MR2854027.
10.14232/ejqtde.2011.1.88
Google Scholar
33 Chiu K.-S. and Pinto M., Variation of parameters formula and Gronwall inequality for differential equations with a general piecewise constant argument, Acta Mathematicae Applicatae Sinica (English Series). (2011) 27, no. 4, 561–568, https://doi.org/10.1007/s10255-011-0107-5, MR2835931, ZBL1270.34169.
10.1007/s10255-011-0107-5
Web of Science® Google Scholar
34 Chiu K.-S. and Pinto M., Periodic solutions of differential equations with a general piecewise constant argument and applications, Electronic Journal of Qualitative Theory of Differential Equations. (2010) 46, 1–19, MR2678388, ZBL1211.34082.
10.14232/ejqtde.2010.1.46
PubMed Web of Science® Google Scholar
35 Chiu K.-S. and Pinto M., Stability of periodic solutions for neural networks with a general piecewise constant argument, Proceedings of the 1st Joint International Meeting AMS-SOMACHI, December 2010, Pucón, Chile.
Google Scholar
36 Chiu K.-S., Periodic solutions for nonlinear integro-differential systems with piecewise constant argument, The Scientific World Journal. In press.
Google Scholar
37 Pinto M., Asymptotic equivalence of nonlinear and quasi linear differential equations with piecewise constant arguments, Mathematical and Computer Modelling. (2009) 49, no. 9-10, 1750–1758, https://doi.org/10.1016/j.mcm.2008.10.001, MR2532088, ZBL1171.34321.
10.1016/j.mcm.2008.10.001
Google Scholar
38 Busenberg S. and Cooke K., V. Lakshmikantham, Models of vertically transmitted diseases with sequential-continuous dynamics, Nonlinear Phenomena in Mathematical Sciences, 1982, Academic Press, New York, NY, USA, 179–187.
10.1016/B978-0-12-434170-8.50028-5
Google Scholar
39 Bereketoglu H., Seyhan G., and Ogun A., Advanced impulsive differential equations with piecewise constant arguments, Mathematical Modelling and Analysis. (2010) 15, no. 2, 175–187, https://doi.org/10.3846/1392-6292.2010.15.175-187, MR2604207, ZBL1218.34095.
10.3846/1392-6292.2010.15.175-187
Web of Science® Google Scholar
40 Karakoc F., Bereketoglu H., and Seyhan G., Oscillatory and periodic solutions of impulsive differential equations with piecewise constant argument, Acta Applicandae Mathematicae. (2010) 110, no. 1, 499–510, https://doi.org/10.1007/s10440-009-9458-9, MR2601669, ZBL1196.34104.
10.1007/s10440-009-9458-9
Web of Science® Google Scholar
41 Huang Z. K., Wang X. H., and Gao F., The existence and global attractivity of almost periodic sequence solution of discrete-time neural networks, Physics Letters A. (2006) 350, no. 3-4, 182–191, https://doi.org/10.1016/j.physleta.2005.10.022.
10.1016/j.physleta.2005.10.022
CAS Web of Science® Google Scholar
42 Cooke K. L. and Wiener J., An equation alternately of retarded and advanced type, Proceedings of the American Mathematical Society. (1987) 99, no. 4, 726–732, https://doi.org/10.2307/2046483, MR877047, ZBL0628.34074.
10.1090/S0002-9939-1987-0877047-8
Web of Science® Google Scholar

All articles

Existence and Global Exponential Stability of Equilibrium for Impulsive Cellular Neural Network Models with Piecewise Alternately Advanced and Retarded Argument

Abstract

1. Introduction

1.1. Piecewise Constant Impulsive Systems

1.2. Model Description

2. Existence and Uniqueness Theorems

2.1. Preliminaries and Definition

2.2. Existence and Uniqueness of Equilibrium

3. Global Exponential Stability of Equilibrium

4. Examples and Simulations

5. Conclusions

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Existence and Global Exponential Stability of Equilibrium for Impulsive Cellular Neural Network Models with Piecewise Alternately Advanced and Retarded Argument

Abstract

1. Introduction

1.1. Piecewise Constant Impulsive Systems

1.2. Model Description

2. Existence and Uniqueness Theorems

2.1. Preliminaries and Definition

2.2. Existence and Uniqueness of Equilibrium

3. Global Exponential Stability of Equilibrium

4. Examples and Simulations

5. Conclusions

Acknowledgments

References

Figures

References

Related

Information