On the Mean Residual Life Function and Stress and Strength Analysis under Different Loss Function for Lindley Distribution
Abstract
Purpose. Mathematical properties of Lindley distribution are derived under different loss functions. These properties include mean residual life function, Lorenz curve, stress and strength characteristic, and their respective posterior risk via simulation scheme. Methodology. Bayesian approach is used for the reliability characteristics. Results are compared on the basis of posterior risk. Findings. Using prior information on the parameter of Lindley distribution, Bayes estimates for reliability characteristics are compared under different loss functions. Practical Implications. Since Lindley distribution is a mixture of gamma and exponential distribution, so Bayesian estimation of reliability characteristics will have a great implication in reliability theory. Originality. A real life application to waiting time data at the bank is also described for the developed procedures. This study is useful for researcher and practitioner in reliability theory.
1. Introduction
Exponential distribution is frequently used as a lifetime distribution in statistics and applied areas; the Lindley distribution has been ignored in the literature since 1958. Lindley distribution originally developed by Lindley [1] and some classical statistic properties are investigated by Ghitany et al. [2]. Sankaran [3] introduced a discrete version of Lindley distribution known as discrete Poisson-Lindley distribution, and Ghitany and Al-Mutairi [4] described some estimation methods. The distribution of zero-truncated Poisson-Lindley was introduced by Ghitany et al. [5] who used the distribution for modeling count data in the case where the distribution has to be adjusted for the count of missing zeros. Zamani and Ismail [6] introduced negative binomial distribution as an alternative to zero-truncated Poisson-Lindley distribution. Recently, Ghitany et al. [7] introduced a two-parameter weighted Lindley distribution and pointed that Lindley distribution is particularly useful in modelling biological data from mortality studies.
The rest of the study is organized as follows. Section 2 deals with the derivation of posterior distribution using different noninformative and informative priors. Using different loss functions, the Bayes estimators and their respective posterior risks are discussed in Section 3. Elicitation of hyperparameter is also discussed in Section 3. Simulation study of Bayes estimates of mean residual life and their posterior risks is performed in Section 4. Lorenz curve discussion for Lindley distribution is given in Section 5 while stress and strength reliability characteristics and simulation study under different loss functions is discussed/performed in Section 6. Real life application is illustrated in Section 7. Finally, Section 8 deals with a conclusion and some future remarks.
2. Likelihood Function and Posterior Distributions
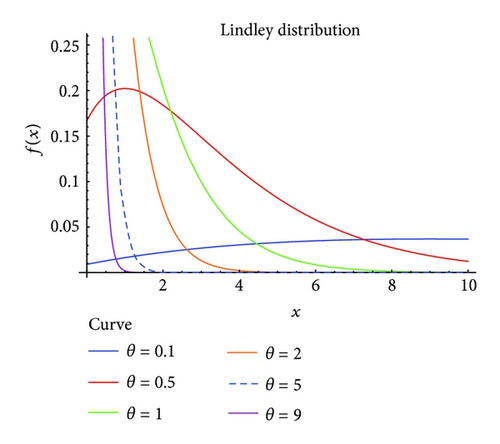
It is obvious from Figure 1 that behavior of Lindley distribution is close to exponential or gamma distribution.
2.1. Posterior Distribution Using Noninformative Priors
2.1.1. Uniform Prior
2.1.2. Jeffreys Prior
2.2. Posterior Distribution Using Informative Prior
In case of an informative prior, the use of prior information is equivalent to adding a number of observations to a given sample size and, therefore, leads to a reduction of the variance/posterior risk of the Bayes estimates. Bansal [9] discussed a method to evaluate the relevance of a prior information in terms of the number of additional observation supposed to be added to a given sample size. We used the gamma and conjugate informative prior for analysis.
2.2.1. Gamma Prior
2.2.2. Likelihood Matching Prior (Conjugate Prior)
3. Bayes Estimators and Posterior Risk under Different Loss Functions
This section spotlight is on the derivation of the Bayes estimator (BE) under different loss functions and their respective posterior risk (PR). The results are compared for noninformative as well as informative priors. If the decision is a choice of an estimator, then, the Bayes decision is a Bayes estimator. The Bayes estimators are evaluated under squared error loss function (SELF), weighted squared error loss function (WSELF), precautionary loss function (PLF), modified (quadratic) squared error loss function (M/Q SELF), logarithmic loss function (SLLF), entropy loss function (ELF), and K-Loss function. K-loss function proposed by Wasan [10] is well fitted for a measure of inaccuracy for an estimator of a scale parameter of a distribution defined on R+ = (0, ∞); this loss function is called K-loss function (KLF). Kanefuji and Iwase [11] used KLF for the estimation of a scale parameter with a known coefficient of variations. Table 1 (by [12]) will show the Bayes estimators and their posterior risks for the above-mentioned loss function.
| Loss function | Bayes estimator (BE) | Posterior risk (PR) |
|---|---|---|
| L1 = SELF = (θ−d)2 | E(θ∣x) | Var(θ∣x) |
| 2 | ||
| L5 = SLLF = (logθ−logd)2 | exp(E(log θ∣x)) | Var (log θ∣x) |
| E(log θ∣x) − log (E(θ−1∣x)) | ||
| 2[E(θ∣x)E(θ−1∣x) − 1] |
3.1. Elicitation of Hyperparameter(s)
Even though many authors have pointed a need for a formal and comprehensive process for elicitation of hyperparameters, there is no standard method. For elicitation, mainly two points are considered; the functional form of the prior distribution and hyperparameter(s), that is why a natural conjugate prior distribution has been generally recommended because its functional form is identical to likelihood function and posterior distribution can be determined by the way of conjugancy. To determine hyperparameter, we adopted the method discussed by Ali et al. [12].
4. Mean Residual Life Function
-
m(0) = μ.
-
m(x) is a decreasing function in x and θ and 1/θ < m(x) < (θ + 2)/(θ(θ + 1)) = μ.
From m(x), one can easily observe that mean residuals life is a diminishing function of time because the distribution belongs to exponential family and for larger parameter value it is close to zero. To evaluate the Bayes estimates and their risk, since the integral appears in both numerator and denumerator, we required a suitable approximate method to obtain Bayes estimates and respective posterior risks. The simplest method is Lindley’s [16] approximation method, which approaches the ratio of the integrals as a whole and produces a single numerical results. Thus, Lindley approximation (LA) given by Lindley [16] for obtaining the Bayes estimator and posterior risk of θ (Mathematica can be used for the solution of integral but takes large time as compared to LA). Many researchers have used this approximation for solving the ratio of integrals for different numbers of parameters for lifetime distributions; see among others Howlader and Hossain [17], Singh et al. [18], and Preda et al. [19].
wherethe simulation study of mean residual life function (MRLF) for different loss functions under different prior is using t = 3 (see Tables 2, 3, 4, 5, 6, 7, and 8).
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 |
|
|
|
|
|
|
| 40 |
|
|
|
|
|
|
| 60 |
|
|
|
|
|
|
| 80 |
|
|
|
|
|
|
| 100 |
|
|
|
|
|
|
| n | LMP | GP | ||||
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 |
|
|
|
|
|
|
| 40 |
|
|
|
|
|
|
| 60 |
|
|
|
|
|
|
| 80 |
|
|
|
|
|
|
| 100 |
|
|
|
|
|
|
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 |
|
|
|
|
|
|
| 40 |
|
|
|
|
|
|
| 60 |
|
|
|
|
|
|
| 80 |
|
|
|
|
|
|
| 100 |
|
|
|
|
|
|
| n | LMP | GP | ||||
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 |
|
|
|
|
|
|
| 40 |
|
|
|
|
|
|
| 60 |
|
|
|
|
|
|
| 80 |
|
|
|
|
|
|
| 100 |
|
|
|
|
|
|
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 |
|
|
|
|
|
|
| 40 |
|
|
|
|
|
|
| 60 |
|
|
|
|
|
|
| 80 |
|
|
|
|
|
|
| 100 |
|
|
|
|
|
|
| n | LMP | GP | ||||
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 |
|
|
|
|
|
|
| 40 |
|
|
|
|
|
|
| 60 |
|
|
|
|
|
|
| 80 |
|
|
|
|
|
|
| 100 |
|
|
|
|
|
|
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 | 16.9211 (0.520576) | 1.1815 (0.042188) | 0.111158 (0.004791) | 17.3777 (0.493072) | 1.2205 (0.039405) | 0.115987 (0.004383) |
| 40 | 17.0582 (0.265186) | 1.18848 (0.021509) | 0.112945 (0.002464) | 17.2934 (0.258053) | 1.20859 (0.020784) | 0.115468 (0.002356) |
| 60 | 17.0648 (0.177533) | 1.19326 (0.014463) | 0.11312 (0.001653) | 17.2229 (0.174329) | 1.20683 (0.012135) | 0.114822 (0.001604) |
| 80 | 17.0966 (0.133627) | 1.1956 (0.010893) | 0.113516 (0.001246) | 17.2158 (0.131813) | 1.20584 (0.010708) | 0.114803 (0.001218) |
| 100 | 17.0883 (0.10698) | 1.19684 (0.008735) | 0.113575 (0.000999) | 17.1838 (0.105815) | 1.20506 (0.008616) | 0.114608 (0.000981) |
| n | LMP | GP | ||||
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 | 16.8904 (0.485218) | 1.18104 (0.034205) | 0.112775 (0.004302) | 17.3612 (0.492507) | 1.21811 (0.033652) | 0.117262 (0.004203) |
| 40 | 17.0425 (0.256431) | 1.18823 (0.020514) | 0.11376 (0.002342) | 17.2848 (0.256428) | 1.20734 (0.020449) | 0.116118 (0.002310) |
| 60 | 17.0543 (0.173642) | 1.19309 (0.011465) | 0.113666 (0.001602) | 17.2171 (0.173498) | 1.20599 (0.011464) | 0.115259 (0.001583) |
| 80 | 17.0886 (0.131689) | 1.19547 (0.010704) | 0.113926 (0.001214) | 17.2114 (0.131609) | 1.20520 (0.010704) | 0.115132 (0.001207) |
| 100 | 17.0819 (0.105019) | 1.19673 (0.008536) | 0.113903 (0.000979) | 17.1803 (0.105017) | 1.20454 (0.008527) | 0.114871 (0.0009735) |
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 | 16.4002 (0.031314) | 1.13929 (0.036423) | 0.106377 (0.043796) | 16.8701 (0.031313) | 1.17967 (0.036422) | 0.111405 (0.043784) |
| 40 | 16.7929 (0.015685) | 1.16697 (0.018282) | 0.110483 (0.021993) | 17.0316 (0.015687) | 1.18743 (0.018286) | 0.113059 (0.021026) |
| 60 | 16.8873 (0.010466) | 1.1788 (0.012203) | 0.111469 (0.014688) | 17.0468 (0.010471) | 1.19253 (0.012205) | 0.113194 (0.014687) |
| 80 | 16.9629 (0.007851) | 1.1847 (0.009157) | 0.112271 (0.011023) | 17.083 (0.007854) | 1.19503 (0.009158) | 0.113571 (0.011024) |
| 100 | 16.9813 (0.006283) | 1.1881 (0.007329) | 0.112576 (0.008823) | 17.0774 (0.006282) | 1.19638 (0.007329) | 0.113618 (0.008826) |
| n | LMP | GP | ||||
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 | 16.3694 (0.031254) | 1.13883 (0.036408) | 0.108011 (0.043296) | 16.8526 (0.031289) | 1.17711 (0.036412) | 0.112809 (0.043172) |
| 40 | 16.7772 (0.015670) | 1.16672 (0.018277) | 0.111303 (0.021016) | 17.0228 (0.015674) | 1.18614 (0.018204) | 0.113742 (0.021026) |
| 60 | 16.8767 (0.010459) | 1.17862 (0.012201) | 0.112016 (0.014542) | 17.0410 (0.010454) | 1.19166 (0.012202) | 0.113645 (0.014523) |
| 80 | 16.955 (0.007847) | 1.18457 (0.009156) | 0.112681 (0.011023) | 17.0786 (0.007845) | 1.19438 (0.009153) | 0.113908 (0.010987) |
| 100 | 16.9749 (0.006280) | 1.18799 (0.007328) | 0.112905 (0.008822) | 17.0739 (0.006286) | 1.19586 (0.007329) | 0.113887 (0.008800) |
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 | 16.1511 (5.57928) | 1.11927 (0.243079) | 0.10415 (0.150269) | 16.6062 (5.53632) | 1.1582 (0.231109) | 0.10896 (0.150136) |
| 40 | 16.6632 (5.63416) | 1.15649 (0.299794) | 0.109296 (0.141658) | 16.8981 (5.62276) | 1.17658 (0.254403) | 0.111815 (0.141275) |
| 60 | 16.7998 (5.64793) | 1.17169 (0.322941) | 0.110663 (0.139528) | 16.9577 (5.64668) | 1.18525 (0.326034) | 0.112362 (0.136368) |
| 80 | 16.8969 (5.65816) | 1.17933 (0.334435) | 0.111659 (0.137915) | 17.0159 (5.62723) | 1.18956 (0.315758) | 0.112945 (0.136815) |
| 100 | 16.9283 (5.6611) | 1.18378 (0.341065) | 0.112084 (0.127363) | 17.0238 (5.67237) | 1.1920 (0.324957) | 0.113117 (0.12645) |
| n | LMP | GP | ||||
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 | 16.1217 (5.53559) | 1.11883 (0.22428) | 0.105691 (0.147276) | 16.5891 (5.53325) | 1.15569 (0.207762) | 0.110343 (0.148622) |
| 40 | 16.6478 (5.6233) | 1.15624 (0.249369) | 0.110091 (0.149015) | 16.8893 (5.62316) | 1.17531 (0.232234) | 0.112492 (0.137587) |
| 60 | 16.7894 (5.64668) | 1.17152 (0.322650) | 0.111199 (0.148555) | 16.9518 (5.61599) | 1.1844 (0.314585) | 0.112811 (0.145671) |
| 80 | 16.889 (5.62725) | 1.1792 (0.314213) | 0.112063 (0.138788) | 17.0115 (5.62175) | 1.18892 (0.310674) | 0.11328 (0.139026) |
| 100 | 16.9220 (5.66035) | 1.18367 (0.320887) | 0.112409 (0.128663) | 17.0202 (5.65197) | 1.19148 (0.35406) | 0.113385 (0.124952) |
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 | 16.404 (0.063125) | 1.13965 (0.073520) | 0.106432 (0.088576) | 16.8667 (0.063124) | 1.17931 (0.073519) | 0.111351 (0.088753) |
| 40 | 16.7939 (0.031494) | 1.16706 (0.036732) | 0.110498 (0.044231) | 17.0307 (0.031159) | 1.18734 (0.036731) | 0.113046 (0.044226) |
| 60 | 16.8877 (0.020986) | 1.17884 (0.024480) | 0.111475 (0.029485) | 17.0464 (0.020987) | 1.19249 (0.024481) | 0.113188 (0.029405) |
| 80 | 16.9632 (0.015733) | 1.18473 (0.018357) | 0.112274 (0.022107) | 17.0828 (0.015732) | 1.19501 (0.018359) | 0.113568 (0.022108) |
| 100 | 16.9815 (0.012586) | 1.18811 (0.014684) | 0.112579 (0.017685) | 17.0773 (0.012585) | 1.19636 (0.014685) | 0.113616 (0.017682) |
| n | LMP | GP | ||||
| θ | 7.142857 | 1.2 | 0.114114 | 7.142857 | 1.2 | 0.114114 |
| 20 | 16.3737 (0.063005) | 1.1392 (0.073491) | 0.108032 (0.088577) | 16.8494 (0.063076) | 1.17679 (0.073498) | 0.112726 (0.087329) |
| 40 | 16.7783 (0.031144) | 1.16681 (0.036724) | 0.111309 (0.044177) | 17.0220 (0.031132) | 1.18606 (0.036726) | 0.113721 (0.043938) |
| 60 | 16.8772 (0.020973) | 1.17867 (0.024476) | 0.112019 (0.029403) | 17.0406 (0.020103) | 1.19163 (0.024469) | 0.113636 (0.029356) |
| 80 | 16.9553 (0.015725) | 1.1846 (0.018355) | 0.112683 (0.022108) | 17.0784 (0.015723) | 1.19436 (0.018358) | 0.113902 (0.022035) |
| 100 | 16.9751 (0.012581) | 1.18801 (0.014683) | 0.112906 (0.017624) | 17.0737 (0.012582) | 1.19585 (0.014681) | 0.113883 (0.017639) |
Using SELF for θ = 7.142857, Bayes estimates are overestimated while for θ = 1.2 and 0.114114 results are underestimated and by increasing sample size these approaches to true parameter values. This behaviour can be observed in all loss functions except PLF. Making comparison between symmetric and asymmetric loss functions, one can easily observes that SELF has smaller posterior risk. Since there is defect in symmetric loss function, that is, SELF assign equal weight to over and under estimation, so we have to look for an alternative choice. In case of asymmetric loss functions; WSELF, SLLF, and PLF can be alternative choices.
5. Lorenz Curve (See Figure 2)
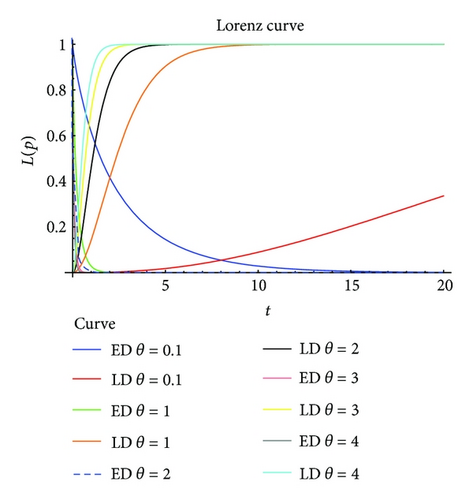
The comparison of Lorenz curve for exponential and Lindley distribution is given in Figures 2 and 3. Lindley distribution performance for Lorenz curve is better as compared to exponential distribution for different values of θ.
6. Stress and Strength Analysis for Lindley Distribution
where P(Y < X) is a relationship which represents the probability that the strength exceeds the stress and f(x, y) is joint p.d.f. of X and Y for example, receptor in human eye operates only if it is simulated by a source where magnitude X is greater than a random lower threshold Y for the eye, so here R is the probability that the receptor operates. In mechanical reliability of a system R gives the probability of a system failure, if the system fails whenever the strength is less than the applied stress.
This quandary has a long narration starting with the revolutionary work of Birnbaum [21] and Birnbaum and McCarty [22]. The stress strength was first introduced by Church and Harris [23]. A comprehensive handling of the different stress strength models can be found in outstanding monograph by Kotz et al. [24]. Some most fresh work on the stress strength model can be found in Kundu and Gupta [25, 26], Raqab and Kundu [27], Kundu and Raqab [28], Krishnamoorthy et al. [29], Eryilmaz [30], and the references cited therein. Recently, Al-Mutairi et al. [31] considered the stress and strength analysis of Lindley distribution using SELF but we are generalizing their work by considering different types of loss functions.
where as both x and y are independent R = 0.026364 (when θ1 = 0.1 and θ2 = 1); R = 0.0604 (for θ1 = 1 and θ2 = 9) and R = 0.998771 (when θ1 = 9 and θ2 = 0.1) (see Tables 9, 10, 11, 12, 13, 14, and 15).
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 | 0.028511 (0.000077) | 0.064361 (0.000288) | 0.998763 (1.44921*10−7) | 0.027985 (0.000078) | 0.063217 (0.000282) | 0.998728 (1.40568*10−7) |
| 60, 80 | 0.027029 (0.000030) | 0.061592 (0.000109) | 0.998756 (6.22876*10−8) | 0.026962 (0.000030) | 0.061386 (0.000109) | 0.998749 (6.19239*10−8) |
| 80, 100 | 0.026832 (0.000023) | 0.061133 (0.000084) | 0.998754 (4.89937*10−8) | 0.026797 (0.000023) | 0.061068 (0.000084) | 0.998749 (4.88093*10−8) |
| 80, 60 | 0.026663 (0.000029) | 0.060702 (0.000105) | 0.998735 (6.74031*10−8) | 0.026796 (0.000029) | 0.061019 (0.000105) | 0.998738 (6.75851*10−8) |
| 100, 60 | 0.026575 (0.000026) | 0.060422 (0.000095) | 0.998733 (6.31669*10−8) | 0.026766 (0.000026) | 0.060865 (0.000095) | 0.99874 (6.31061*10−8) |
| n | LMP | GP | ||||
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 | 0.028581 (0.000076) | 0.064860 (0.000281) | 0.99874 (1.40336*10−7) | 0.027987 (0.000078) | 0.063762 (0.000280) | 0.99871 (1.37326*10−7) |
| 60, 80 | 0.027051 (0.000029) | 0.061760 (0.000109) | 0.998748 (6.18727*10−8) | 0.026956 (0.000029) | 0.061625 (0.000108) | 0.998743 (6.1525*10−8) |
| 80, 100 | 0.026848 (0.000022) | 0.061323 (0.000083) | 0.998748 (4.87444*10−8) | 0.026792 (0.000022) | 0.061255 (0.000083) | 0.998745 (4.85798*10−8) |
| 80, 60 | 0.026676 (0.000028) | 0.061014 (0.000105) | 0.998729 (6.69801*10−8) | 0.026781 (0.000028) | 0.061306 (0.000104) | 0.998733 (6.73044*10−8) |
| 100, 60 | 0.026585 (0.000026) | 0.060732 (0.000094) | 0.998728 (6.28193*10−8) | 0.026748 (0.000026) | 0.061143 (0.000094) | 0.998736 (6.23054*10−8) |
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 | 0.025616 (0.002896) | 0.059646 (0.004714) | 0.998762 (1.4508*10−7) | 0.025146 (0.002839) | 0.058595 (0.004622) | 0.998728 (1.40713*10−7) |
| 60, 80 | 0.025913 (0.001116) | 0.059791 (0.001801) | 0.998756 (6.2361*10−8) | 0.025849 (0.001113) | 0.059591 (0.001795) | 0.998749 (6.1996*10−8) |
| 80, 100 | 0.025971 (0.000860) | 0.059748 (0.001384) | 0.998754 (4.90522*10−8) | 0.025938 (0.000859) | 0.059685 (0.001383) | 0.998749 (4.88671*10−8) |
| 80, 60 | 0.025571 (0.001092) | 0.058960 (0.001742) | 0.998735 (6.74825*10−8) | 0.025699 (0.001091) | 0.059267 (0.001742) | 0.998738 (6.74652*10−8) |
| 100, 60 | 0.025581 (0.000993) | 0.058846 (0.001576) | 0.998733 (6.32415*10−8) | 0.025765 (0.009991) | 0.059276 (0.001568) | 0.99874 (6.31859*10−8) |
| n | CP | GP | ||||
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 | 0.025679 (0.002801) | 0.060117 (0.004543) | 0.99874 (1.40486*10−7) | 0.025148 (0.002839) | 0.059091 (0.004571) | 0.99871 (1.37462*10−7) |
| 60, 80 | 0.025934 (0.001111) | 0.059954 (0.001786) | 0.998748 (6.19446*10−8) | 0.025843 (0.001110) | 0.059822 (0.001702) | 0.998743 (6.15958*10−8) |
| 80, 100 | 0.025987 (0.000860) | 0.059934 (0.001382) | 0.998748 (4.8802*10−8) | 0.025933 (0.000859) | 0.059869 (0.001382) | 0.998745 (4.86369*10−8) |
| 80, 60 | 0.025584 (0.001092) | 0.059262 (0.001741) | 0.998729 (6.70581*10−8) | 0.025684 (0.001091) | 0.059548 (0.001737) | 0.998733 (6.70385*10−8) |
| 100, 60 | 0.025591 (0.000993) | 0.059146 (0.001558) | 0.998728 (6.28928*10−8) | 0.025747 (0.00990) | 0.059549 (0.001553) | 0.998736 (6.23805*10−8) |
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 | 0.023332 (0.999986) | 0.055666 (0.999815) | 0.998762 (0.003708) | 0.023021 (0.999987) | 0.054887 (0.999813) | 0.998728 (0.003812) |
| 60, 80 | 0.024906 (0.999984) | 0.058118 (0.999798) | 0.998756 (0.003728) | 0.024851 (0.999984) | 0.057935 (0.999800) | 0.998749 (0.003729) |
| 80, 100 | 0.025178 (0.999984) | 0.058442 (0.999796) | 0.998754 (0.003734) | 0.025149 (0.999984) | 0.058385 (0.999797) | 0.998749 (0.003734) |
| 80, 60 | 0.024596 (0.999985) | 0.057357 (0.999806) | 0.998735 (0.003790) | 0.024705 (0.999984) | 0.057630 (0.999803) | 0.998738 (0.003780) |
| 100, 60 | 0.024689 (0.999984) | 0.057390 (0.999806) | 0.998733 (0.003796) | 0.024846 (0.999984) | 0.057777 (0.999802) | 0.99874 (0.003776) |
| n | LMP | GP | ||||
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 | 0.023375 (0.999986) | 0.056022 (0.999811) | 0.99874 (0.003706) | 0.023023 (0.999987) | 0.055252 (0.999802) | 0.998709 (0.003666) |
| 60, 80 | 0.024924 (0.999984) | 0.058258 (0.999797) | 0.998748 (0.003721) | 0.024847 (0.999984) | 0.058141 (0.999796) | 0.998743 (0.003727) |
| 80, 100 | 0.025191 (0.999984) | 0.058613 (0.999794) | 0.998748 (0.003732) | 0.025144 (0.999984) | 0.058552 (0.999795) | 0.998745 (0.003731) |
| 80, 60 | 0.024607 (0.999985) | 0.057626 (0.999803) | 0.998728 (0.003780) | 0.024692 (0.999984) | 0.057881 (0.99980) | 0.998733 (0.003759) |
| 100, 60 | 0.024697 (0.999984) | 0.057659 (0.999803) | 0.998728 (0.003712) | 0.024831 (0.999984) | 0.058025 (0.99980) | 0.998736 (0.003708) |
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 | 0.029827 (0.002631) | 0.066557 (0.004393) | 0.998763 (1.451*10−7) | 0.029348 (0.002628) | 0.065490 (0.004345) | 0.998728 (1.4747*10−7) |
| 60, 80 | 0.027570 (0.001082) | 0.062474 (0.001764) | 0.998756 (6.23652*10−8) | 0.027506 (0.001087) | 0.062271 (0.001769) | 0.998749 (6.24015*10−8) |
| 80, 100 | 0.027252 (0.000841) | 0.061814 (0.001363) | 0.998754 (4.90548*10−8) | 0.027219 (0.000843) | 0.061751 (0.001361) | 0.998749 (4.88704*10−8) |
| 80, 60 | 0.027198 (0.001070) | 0.061565 (0.001725) | 0.998735 (6.74885*10−8) | 0.027326 (0.001059) | 0.061873 (0.001707) | 0.998738 (6.75706*10−8) |
| 100, 60 | 0.027064 (0.000979) | 0.061206 (0.001568) | 0.998733 (6.3247*10−8) | 0.027248 (0.000966) | 0.061638 (0.001546) | 0.99874 (6.32386*10−8) |
| n | LMP | GP | ||||
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 | 0.0298893 (0.002617) | 0.067019 (0.004317) | 0.99874 (1.42516*10−7) | 0.029351 (0.002627) | 0.066001 (0.004417) | 0.99871 (1.37503*10−7) |
| 60, 80 | 0.027591 (0.001080) | 0.062633 (0.001748) | 0.998748 (6.19503*10−8) | 0.027500 (0.001080) | 0.062503 (0.001746) | 0.998743 (6.16024*10−8) |
| 80, 100 | 0.027268 (0.000839) | 0.061999 (0.001354) | 0.998748 (4.88056*10−8) | 0.027214 (0.000834) | 0.061934 (0.001347) | 0.998745 (4.86409*10−8) |
| 80,60 | 0.027211 (0.001058) | 0.061868 (0.001707) | 0.998729 (6.70654*10−8) | 0.027311 (0.001060) | 0.062150 (0.001689) | 0.998733 (6.69898*10−8) |
| 100, 60 | 0.027074 (0.000958) | 0.061508 (0.001543) | 0.998728 (6.28994*10−8) | 0.027231 (0.000957) | 0.061908 (0.001529) | 0.998736 (6.23856*10−8) |
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 | 0.027033 (0.11001) | 0.061970 (0.077534) | 0.998762 (1.4526*10−7) | 0.026509 (0.109867) | 0.060832 (0.077376) | 0.998728 (1.40892*10−7) |
| 60, 80 | 0.026465 (0.042628) | 0.060684 (0.029901) | 0.998756 (6.24387*10−8) | 0.026398 (0.042621) | 0.060480 (0.029899) | 0.998749 (6.20736*10−8) |
| 80, 100 | 0.026398 (0.032862) | 0.060436 (0.023035) | 0.998754 (4.91134*10−8) | 0.026363 (0.032859) | 0.060372 (0.023033) | 0.998749 (4.89283*10−8) |
| 80, 60 | 0.026109 (0.042241) | 0.059822 (0.029329) | 0.998735 (6.7568*10−8) | 0.026243 (0.042241) | 0.060138 (0.029323) | 0.998738 (6.75607*10−8) |
| 100, 60 | 0.026071 (0.038466) | 0.059625 (0.026609) | 0.998733 (6.33217*10−8) | 0.026262 (0.038458) | 0.060068 (0.026605) | 0.99874 (6.32621*10−8) |
| n | LMP | GP | ||||
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 | 0.027104 (0.109771) | 0.062474 (0.077367) | 0.99874 (1.40666*10−7) | 0.026511 (0.109817) | 0.061372 (0.077337) | 0.99871 (1.37639*10−7) |
| 60, 80 | 0.026487 (0.042620) | 0.060853 (0.029893) | 0.998748 (6.20223*10−8) | 0.026392 (0.042619) | 0.060718 (0.029804) | 0.998743 (6.16733*10−8) |
| 80, 100 | 0.026414 (0.032860) | 0.060626 (0.023029) | 0.998748 (4.88632*10−8) | 0.026358 (0.032858) | 0.060559 (0.023030) | 0.998745 (4.8698*10−8) |
| 80, 60 | 0.026123 (0.042240) | 0.060133 (0.029322) | 0.998729 (6.71435*10−8) | 0.026227 (0.042235) | 0.060425 (0.029307) | 0.998733 (6.7069*10−8) |
| 100, 60 | 0.026081 (0.038459) | 0.059934 (0.026602) | 0.998728 (6.29729*10−8) | 0.026244 (0.038455) | 0.060347 (0.026580) | 0.998736 (6.24607*10−8) |
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 |
|
|
|
|
|
|
| 60, 80 |
|
|
|
|
|
|
| 80, 100 |
|
|
|
|
|
|
| 80, 60 |
|
|
|
|
|
|
| 100, 60 |
|
|
|
|
|
|
| n | LMP | GP | ||||
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 |
|
|
|
|
|
|
| 60, 80 |
|
|
|
|
|
|
| 80, 100 |
|
|
|
|
|
|
| 80, 60 |
|
|
|
|
|
|
| 100, 60 |
|
|
|
|
|
|
| n | UP | JP | ||||
|---|---|---|---|---|---|---|
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 |
|
|
0.998762 (2.9052*10−7) |
|
|
0.998728 (2.81784*10−7) |
| 60, 80 |
|
|
0.998756 (1.24877*10−7) |
|
|
0.998749 (1.24147*10−7) |
| 80, 100 |
|
|
0.998754 (9.82267*10−8) |
|
|
0.998749 (9.78566*10−8) |
| 80, 60 |
|
|
0.998735 (1.35136*10−7) |
|
|
0.998738 (1.35101*10−7) |
| 100, 60 |
|
|
0.998733 (1.26643*10−7) |
|
|
0.99874 (1.26324*10−7) |
| n | LMP | GP | ||||
| R | 0.026364 | 0.0604 | 0.998771 | 0.026364 | 0.0604 | 0.998771 |
| 20, 40 |
|
|
0.99874 (2.81332*10−7) |
|
|
0.99871 (2.75278*10−7) |
| 60, 80 |
|
|
0.998748 (1.24045*10−7) |
|
|
0.998743 (1.23347*10−7) |
| 80, 100 |
|
|
0.998748 (9.77264*10−8) |
|
|
0.998745 (9.73961*10−8) |
| 80, 60 |
|
|
0.998729 (1.34287*10−7) |
|
|
0.998733 (1.34238*10−7) |
| 100, 60 |
|
|
0.998728 (1.25946*10−7) |
|
|
0.998736 (1.25921*10−7) |
The Bayes estimates of stress and strength under SELF, MSELF, and ELF are underestimated. By comparing symmetric and asymmetric loss functions, it is noted that posterior risk of SELF is smaller than asymmetric loss functions. In case of asymmetric loss functions, WSELF and PLF have smaller posterior risk than other available loss functions.
Evaluating the performance of informative and noninformative priors, one can easily observe that informative priors have smaller posterior risk due to the availability of compact information. LM and gamma priors both have approximately the same behaviour depending upon the choice of hyperparameters value. More compact information will lead to correct hyperparameters which will lead to definitely better results and smaller posterior risk than noninformative priors. Although there are some depicts where informative priors have posterior risks greater than noninformative priors which is just due to random generation. Increasing sample size in case of SLLF has an inverse effect.
7. Real Life Application
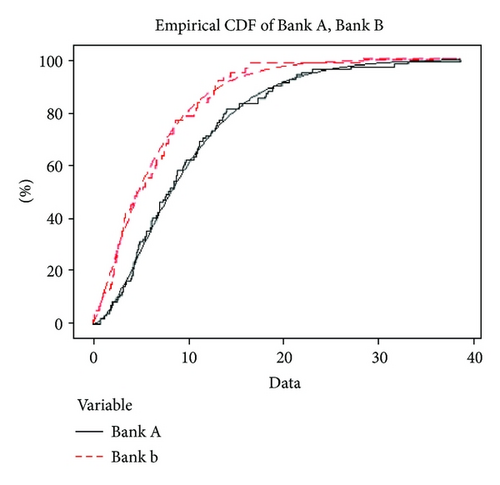
Ghitany et al. [2] provide waiting times (in minutes) before service of 100 bank customers data set for Lindley distribution. They fitted both Lindley and exponential distributions (both have the same number of parameters) by method of maximized likelihood method and found Lindley distribution provides better fit. The data is given in Tables 16 and 17.
| 0.8 | 2.9 | 4.3 | 5.0 | 6.7 | 8.2 | 9.7 | 11.9 | 14.1 | 19.9 |
| 0.8 | 3.1 | 4.3 | 5.3 | 6.9 | 8.6 | 9.8 | 12.4 | 15.4 | 20.6 |
| 1.3 | 3.2 | 4.4 | 5.5 | 7.1 | 8.6 | 10.7 | 12.5 | 15.4 | 21.3 |
| 1.5 | 3.3 | 4.4 | 5.7 | 7.1 | 8.6 | 10.9 | 12.9 | 17.3 | 21.4 |
| 1.8 | 3.5 | 4.6 | 5.7 | 7.1 | 8.8 | 11.0 | 13.0 | 17.3 | 21.9 |
| 1.9 | 3.6 | 4.7 | 6.1 | 7.1 | 8.8 | 11.0 | 13.1 | 18.1 | 23.0 |
| 1.9 | 4.0 | 4.7 | 6.2 | 7.4 | 8.9 | 11.1 | 13.3 | 18.2 | 27.0 |
| 2.1 | 4.1 | 4.8 | 6.2 | 7.6 | 8.9 | 11.2 | 13.6 | 18.4 | 31.6 |
| 2.6 | 4.2 | 4.9 | 6.2 | 7.7 | 9.5 | 11.2 | 13.7 | 18.9 | 33.1 |
| 2.7 | 4.2 | 4.9 | 6.3 | 8.0 | 9.6 | 11.5 | 13.9 | 19.0 | 38.5 |
| 0.1 | 1.2 | 2.3 | 2.9 | 3.5 | 5.3 | 6.8 | 8.0 | 8.5 | 13.2 |
| 0.2 | 1.8 | 2.3 | 3.1 | 3.9 | 5.6 | 7.3 | 8.5 | 11.0 | 13.7 |
| 0.3 | 1.9 | 2.5 | 3.1 | 4.0 | 5.6 | 7.5 | 8.7 | 12.1 | 14.5 |
| 0.7 | 2.0 | 2.6 | 3.2 | 4.2 | 6.2 | 7.7 | 9.5 | 12.3 | 16.0 |
| 0.9 | 2.2 | 2.7 | 3.4 | 4.5 | 6.3 | 7.7 | 10.7 | 12.8 | 16.5 |
| 1.1 | 2.3 | 2.7 | 3.4 | 4.7 | 6.6 | 8.0 | 10.9 | 12.9 | 28.0 |
We fit on both data sets Kolmogorov-Smirnov test and found that Lindley distribution is good fitted. The values of K-S test along P value are given in Table 18.
| Data set | K-S test | P value | MLE |
|---|---|---|---|
| Bank A | 0.065 | 0.721 | 0.187 |
| Bank B | 0.083 | 0.826 | 0.280 |
The Bayes estimates of stress and strength reliability under different priors and their posterior risk are evaluated in Tables 19 and 20.
| ↓ Loss function∣prior→ | UP | JP | LMP | GP |
|---|---|---|---|---|
| SELF | 0.354572 (0.001590) | 0.35578 (0.001588) | 0.354518 (0.001589) | 0.355719 (0.001588) |
| WSELF | 0.350132 (0.004439) | 0.351317 (0.004436) | 0.35008 (0.004438) | 0.351257 (0.004432) |
| MSELF | 0.345899 (0.958108) | 0.347017 (0.957694) | 0.34585 (0.957126) | 0.346961 (0.957115) |
| PLF | 0.356806 (0.004470) | 0.358004 (0.004448) | 0.356754 (0.004470) | 0.357944 (0.004449) |
| SLLF | 0.352333 (0.012639) | 0.353537 (0.012664) | 0.35228 (0.012637) | 0.353476 (0.012663) |
| ELF | 0.350132 (2.09262) | 0.351317 (2.08584) | 0.35008 (2.09292) | 0.351257 (2.08618) |
| KLF | 0.352345 (0.025358) | 0.353541 (0.023508) | 0.352292 (0.025354) | 0.353481 (0.025307) |
| ↓ Loss function∣prior→ | UP | JP | LMP | GP |
|---|---|---|---|---|
| SELF | 8.40917 (0.477926) | 8.45888 (0.475225) | 8.40618 (0.477931) | 8.45692 (0.475245) |
| WSELF | 8.35267 (0.056499) | 8.40204 (0.056847) | 8.34973 (0.056459) | 8.40007 (0.056485) |
| MSELF | 8.29763 (574.087) | 8.34567 (584.203) | 8.29478 (573.489) | 8.34375 (583.797) |
| PLF | 8.43754 (0.056738) | 8.48693 (0.056088) | 8.43456 (0.056735) | 8.48498 (0.056124) |
| SLLF | 8.38079 (0.006753) | 8.43049 (0.006754) | 8.37781 (0.006750) | 8.42852 (0.006754) |
| ELF | 8.35267 (4.24852) | 8.40204 (4.26033) | 8.34973 (4.24782) | 8.40007 (4.23986) |
| KLF | 8.38088 (0.013528) | 8.43041 (0.013531) | 8.37791 (0.013523) | 8.42845 (0.013524) |
Since the Lindley distribution belongs to the exponential family so the natural conjugate prior is Gamma distribution.
The posterior risks of LMP and GP are approximately the same as compared to noninformative priors. There are some posterior risk values which are greater than noninformative priors. These are just due to hyperparameters value effect that is, more accurate values will lead to the smaller posterior risk. PLF and WSELF loss functions have smaller posterior risk as compared to other loss functions.
8. Conclusion and Suggestions
The choice of loss function as concerned, one can easily observe based on evidence (different properties as discussed above) that PLF, SLLF, and WSELF are suitable than other asymmetrical loss functions. One thing is common as we increase sample size posterior risk comes down. In future, this work can be extended using censored data.




