A Numerical Solution to Fractional Diffusion Equation for Force-Free Case
Abstract
A collocation finite element method for solving fractional diffusion equation for force-free case is considered. In this paper, we develop an approximation method based on collocation finite elements by cubic B-spline functions to solve fractional diffusion equation for force-free case formulated with Riemann-Liouville operator. Some numerical examples of interest are provided to show the accuracy of the method. A comparison between exact analytical solution and a numerical one has been made.
1. Introduction
Scientific and engineering problems including fractional derivatives have become more important in recent years. Since the description of physical and chemical processes by means of equations including fractional derivatives is more accurate and precise, their numerical solutions have been the primary interest of many recently published articles. The applications are so wide that they include such diverse areas as control theory [1], transport problems [2], tumor development [3], subdiffusive anomalous transport in the presence of an external field [4–7], and viscoelastic and viscoplastic flow [8]. These diverse areas of applications have led to an increase in the number of studies on fractional differential equations and have caused it to be an important topic in mathematics and science. Yuste [9] has used weighted average finite difference methods for fractional diffusion equations and provided some examples in which the new methods′ numerical solutions are obtained and compared against exact solutions. Langlands and Henry [10] have investigated the accuracy and stability of an implicit numerical scheme for solving the fractional diffusion equation. Murio [11] has developed an implicit unconditionally stable numerical method to solve the one-dimensional linear time fractional diffusion equation, formulated with Caputo′s fractional derivative, on a finite slab. Yuste and Acedo [12] have combined the forward time centered space (FTCS) method, well known for the numerical integration of ordinary diffusion equations, with the Grünwald-Letnikov discretization of the Riemann-Liouville derivative to obtain an FTCS scheme for solving the fractional diffusion equation.
2. Cubic B-Spline Finite Element Collocation Solutions
2.1. Initial State
Solving this system yields the values of element parameters at t = 0. Now, it is time to find out the values of element parameters at different time levels using the iterative system (15).
2.2. Stability Analysis
3. Numerical Examples and Results
Figures 1 and 2 show the graphs of the exact (denoted by lines) solutions and the numerical ones for Δt = 0.0001 and N = 40 at t = 0.001 (denoted by triangles), t = 0.01 (denoted by squares), and t = 0.1 (denoted by stars) for two different values of γ = 0.50 and γ = 0.75, respectively. Table 1 shows the comparison of the exact solutions with the numerical ones with γ = 0.5, Δt = 0.001, and tf = 0.1 for different values of N. The calculated error norms L2 and L∞ at those time levels are also presented in the table. In Table 2, the comparison of the exact solutions with the numerical ones with γ = 0.5, N = 40 and tf = 0.1 for different values of Δt is illustrated and then the error norms L2 and L∞ are computed and presented in the table. In Table 3, we have listed the numerical and exact solutions of the problem for γ = 0.75, Δt = 0.001, and tf = 0.1 for different values of N and the error norms L2 and L∞. Table 4 illustrates the comparison of the exact solutions with the numerical solutions for γ = 0.75, N = 40, and tf = 0.1 for different values of Δt and the error norms L2 and L∞.
| x | N = 10 | N = 20 | N = 40 | N = 80 | N = 100 | Exact |
|---|---|---|---|---|---|---|
| 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 0.1 | 0.013806 | 0.013886 | 0.013920 | 0.013925 | 0.013926 | 0.013765 |
| 0.2 | 0.026128 | 0.026284 | 0.026325 | 0.026335 | 0.026336 | 0.026183 |
| 0.3 | 0.035777 | 0.035982 | 0.036034 | 0.036046 | 0.036048 | 0.036037 |
| 0.4 | 0.041903 | 0.042137 | 0.042195 | 0.042210 | 0.042212 | 0.042364 |
| 0.5 | 0.044001 | 0.044245 | 0.044306 | 0.044321 | 0.044323 | 0.044544 |
| 0.6 | 0.041903 | 0.042137 | 0.042195 | 0.042210 | 0.042212 | 0.042364 |
| 0.7 | 0.035777 | 0.035982 | 0.036034 | 0.036046 | 0.036048 | 0.036037 |
| 0.8 | 0.026128 | 0.026284 | 0.026325 | 0.026335 | 0.026336 | 0.026183 |
| 0.9 | 0.013806 | 0.013886 | 0.013920 | 0.013925 | 0.013926 | 0.013765 |
| 1.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| L2 × 103 | 0.294172 | 0.159576 | 0.142246 | 0.139756 | 0.139501 | |
| L∞ × 103 | 0.543026 | 0.299690 | 0.238942 | 0.223758 | 0.221936 | |
| x | Δt = 0.01 | Δt = 0.001 | Δt = 0.0001 | Δt = 0.00001 | Exact |
|---|---|---|---|---|---|
| 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 0.1 | 0.015039 | 0.013920 | 0.013929 | 0.013930 | 0.013765 |
| 0.2 | 0.026111 | 0.026325 | 0.026347 | 0.026349 | 0.026183 |
| 0.3 | 0.035392 | 0.036034 | 0.036063 | 0.036065 | 0.036037 |
| 0.4 | 0.041638 | 0.042195 | 0.042229 | 0.042233 | 0.042364 |
| 0.5 | 0.043830 | 0.044306 | 0.044341 | 0.044345 | 0.044544 |
| 0.6 | 0.041638 | 0.042195 | 0.042229 | 0.042233 | 0.042364 |
| 0.7 | 0.035392 | 0.036034 | 0.036063 | 0.036065 | 0.036037 |
| 0.8 | 0.026111 | 0.026325 | 0.026347 | 0.026349 | 0.026183 |
| 0.9 | 0.015039 | 0.013920 | 0.013929 | 0.013930 | 0.013765 |
| 1.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| L2 × 103 | 0.836889 | 0.142246 | 0.136548 | 0.136264 | |
| L∞ × 103 | 1.589369 | 0.238942 | 0.203235 | 0.199723 | |
| x | N = 10 | N = 20 | N = 40 | N = 80 | N = 100 | Exact |
|---|---|---|---|---|---|---|
| 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 0.1 | 0.018544 | 0.018677 | 0.018710 | 0.018718 | 0.018719 | 0.018574 |
| 0.2 | 0.035151 | 0.035393 | 0.035453 | 0.035468 | 0.035470 | 0.035331 |
| 0.3 | 0.048210 | 0.048531 | 0.048611 | 0.048631 | 0.048633 | 0.048629 |
| 0.4 | 0.056530 | 0.056900 | 0.056992 | 0.057015 | 0.057018 | 0.057166 |
| 0.5 | 0.048210 | 0.059771 | 0.059868 | 0.059892 | 0.059895 | 0.060108 |
| 0.6 | 0.056530 | 0.056900 | 0.056992 | 0.057015 | 0.057018 | 0.057166 |
| 0.7 | 0.048210 | 0.048531 | 0.048611 | 0.048631 | 0.048633 | 0.048629 |
| 0.8 | 0.035151 | 0.035393 | 0.035453 | 0.035468 | 0.035470 | 0.035331 |
| 0.9 | 0.018544 | 0.018677 | 0.018710 | 0.018718 | 0.018719 | 0.018574 |
| 1.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| L2 × 103 | 0.418167 | 0.174101 | 0.136253 | 0.130959 | 0.130466 | |
| L∞ × 103 | 0.722901 | 0.336912 | 0.240523 | 0.216433 | 0.213542 | |
| x | Δt = 0.01 | Δt = 0.001 | Δt = 0.0001 | Δt = 0.00001 | Exact |
|---|---|---|---|---|---|
| 0.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| 0.1 | 0.018556 | 0.018710 | 0.018722 | 0.018723 | 0.018574 |
| 0.2 | 0.035089 | 0.035453 | 0.035475 | 0.035477 | 0.035331 |
| 0.3 | 0.048219 | 0.048611 | 0.048642 | 0.048644 | 0.048629 |
| 0.4 | 0.056522 | 0.056992 | 0.057028 | 0.057031 | 0.057166 |
| 0.5 | 0.059360 | 0.059868 | 0.059905 | 0.059909 | 0.060108 |
| 0.6 | 0.056522 | 0.056992 | 0.057028 | 0.057031 | 0.057166 |
| 0.7 | 0.048219 | 0.048611 | 0.048642 | 0.048644 | 0.048629 |
| 0.8 | 0.035089 | 0.035453 | 0.035475 | 0.035477 | 0.035331 |
| 0.9 | 0.018556 | 0.018710 | 0.018722 | 0.018723 | 0.018574 |
| 1.0 | 0.000000 | 0.000000 | 0.000000 | 0.000000 | 0.000000 |
| L2 × 103 | 0.449135 | 0.136253 | 0.128451 | 0.127966 | |
| L∞ × 103 | 0.747758 | 0.240523 | 0.203042 | 0.199418 | |
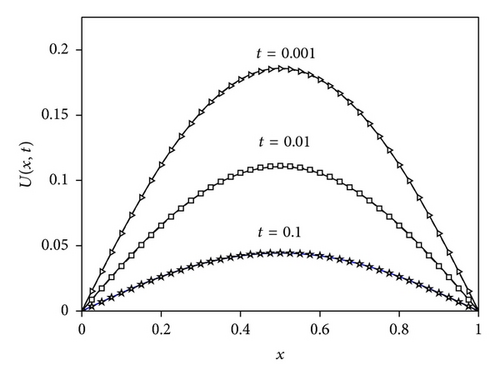
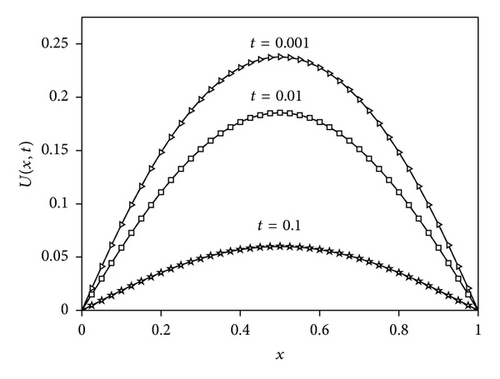
4. Conclusion
In the present study, first of all, a collocation finite element method has been constructed. Then, the method has been applied using cubic B-spline base functions. During the implementation of the method, Crank-Nicolson formula and first-order difference formula have been applied for discretization process. The stability of the method presented in the paper has been tested using the von Neumann stability analysis in which the growth factor of a typical Fourier mode is used. The accuracy of the method is also measured by the error norms L2 and L∞. The successful application of the present method prompts the probability of extending it to other finite element methods and other kinds of fractional differential equations. The available results suggest that this is highly probable.




