Abstract and Applied Analysis
Volume 2013, Issue 1 178378
Research Article
Open Access

On Solutions of Linear Fractional Differential Equations with Uncertainty

T. Allahviranloo, 

T. Allahviranloo

Department of Electronic and Communications, Faculty of Engineering, Izmir University, Izmir, Turkey

Search for more papers by this author
S. Abbasbandy, 

S. Abbasbandy

Department of Mathematics, Science and Research Branch, Islamic Azad University, Tehran, Iran iau.ac.ir

Search for more papers by this author
M. R. Balooch Shahryari, 

M. R. Balooch Shahryari

Department of Mathematics, Science and Research Branch, Islamic Azad University, Tehran, Iran iau.ac.ir

Search for more papers by this author
S. Salahshour, 

Corresponding Author

S. Salahshour

Young Researchers and Elite Club, Mobarakeh Branch, Islamic Azad University, Mobarakeh, Iran mau.ac.ir

Search for more papers by this author
D. Baleanu, 

D. Baleanu

Department of Chemical and Materials Engineering, Faculty of Engineering, King Abdulaziz University, Jeddah 21589, Saudi Arabia

Department of Mathematics and Computer Sciences, Faculty of Arts and Sciences, Cankaya University, 06530 Ankara, Turkey

Institute of Space Sciences, Magurele-Bucharest, Bucharest, RO 7690, Romania

Search for more papers by this author
First published: 21 November 2013
https://doi.org/10.1155/2013/178378
Citations: 7
Academic Editor: Ali H. Bhrawy

Abstract

The solutions of linear fuzzy fractional differential equations (FFDEs) under the Caputo differentiability have been investigated. To this end, the fuzzy Laplace transform was used to obtain the solutions of FFDEs. Then, some new results regarding the relation between some types of differentiability have been obtained. Finally, some applicable examples are solved in order to show the ability of the proposed method.

1. Introduction

The topic of fuzzy differential equations (FDEs) has been rapidly growing in recent years (see, e.g., [1–8] and the references therein). Recently, applying fractional differential equations has grown increasingly and have excited as a considerable interest both in mathematics and applications, such that they were used in modeling of many physical and chemical processes and in engineering [9–15].

In addition, many research papers are published to consider solutions of fractional differential equations (see, e.g., [16–18] and the references therein).

Recently, Agarwal et al. [19] proposed the concept of solutions for fractional differential equations with uncertainty. They considered the Riemann-Liouville differentiability to solve FFDEs which is a combination of Hukuhara difference and Riemann-Liouville derivative. There are some basic papers which are written by Bede and Gal [20] who discussed on shortcomings of applications of Hukuhara difference. So, we adopt a generalization of a strongly generalized differentiability to a fractional case.

In the following, we propose the Riemann-Liouville differentiability by using Hukuhara difference which is named as the Riemann-Liouville H-differentiability. Therefore, a direct procedure is adopted to derive such concept which is constructed based on the combination of strongly generalized differentiability [21] and the Riemann-Liouville derivative [14, 15]. Moreover, we suggest the concept of fractional derivatives under Caputo’s differentiability by applying the Hukuhara difference which is named as Caputo’s H-differentiability. Similar to the deterministic cases, construction of Caputo’s derivatives is based on the definitions of the Riemann-Liouville derivatives in fuzzy cases.

Consequently, we intend to propose an analytical method to solve FFDEs. Since, considering solutions of FFDEs is a new subject, presets the fractional Green’s functions for fuzzy fractional differential equations is considered and, as particular cases, we obtain the classical harmonic oscillator, the damped harmonic oscillator, relaxation equation, all in the fuzzy fractional versions by using fuzzy laplace transforms; so we should first implement analytical method to solve it; then numerical methods can be applied. To this end, we adopt fractional Green’s functions to solve FFDEs by using fuzzy Laplace transforms method. One can see some useful papers about fuzzy Laplace transforms in [2, 22, 23].

Recently, Salahshour et al. proposed some new results toward existence and uniqueness of the solutions of FFDE [24]. Then, Mazandarani and Kamyad numerically solved the FFDE using the Euler method [25]. Also, Agarwal et al. [26] investigated fuzzy fractional integral equation under compactness type condition.

This paper is structured as follows. In Section 1, we recall some well-known definitions of fuzzy numbers and present some needed concepts. In Section 2, Caputo’s H-differentiability is introduced, and the relation between the Riemann-Liouville differentiability and Caputo’s H-differentiability and some of their properties is considered. Consequently, the fuzzy Laplace transforms are considered for fuzzy-valued function, and an essential theorem for the Laplace transform of f under Caputo’s H-derivative is given in Section 3. The solutions of FFDEs are investigated by using the fuzzy Laplace transforms and their inverses in Section 4. In Section 5, some examples are solved to illustrate the method. Finally, conclusion is drawn in Section 6.

2. Preliminaries

The basic definition of fuzzy numbers can be seen in [27].

We denote by ℝ the set of all real numbers and the set of all fuzzy numbers on ℝ is indicated by 𝔼. A fuzzy number is a mapping u : ℝ → [0,1] with the following properties.
  • (a)

    u  is upper semicontinuous.

  • (b)

    u is fuzzy convex; that is, u(λx + (1 − λ)y) ≥ min {u(x), u(y)} for all x, y ∈ ℝ, λ ∈ [0,1].

  • (c)

    u is normal; that is; ∃x0 ∈ ℝ for which u(x0) = 1.

  • (d)

    supp u = {x ∈ ℝ∣u(x) > 0} is the support of the u, and its closure cl (supp u) is compact.

An equivalent parametric definition is also given in [28–30] as follows.

Definition 1. A fuzzy number u in parametric form is a pair of functions , , 0 ≤ r ≤ 1, which satisfy the following requirements:

  • (1)

    is a bounded nondecreasing left continuous function in (0,1]; and right continuous at 0;

  • (2)

      is a bounded nonincreasing left continuous function in (0,1]; and right continuous at 0;

  • (3)

     ,  0 ≤ r ≤ 1.

Moreover, we also can present the r-cut representation of fuzzy number as for all 0 ≤ r ≤ 1.

According to Zadeh’s extension principle, operation of addition on 𝔼 is defined by
()
and scalar multiplication of a fuzzy number is given by
()
where .
The Hausdorff distance between fuzzy numbers is given by d : 𝔼 × 𝔼 → ℝ+ ∪ {0},
()
where , is utilized in [20]. Then, it is easy to see that d is a metric in 𝔼 and has the following properties (see [31]):
  • (1)

    d(u + w, v + w) = d(u, v), for all u, v, w ∈ 𝔼,

  • (2)

    d(ku, kv) = |k|d(u, v), for all k ∈ ℝ, u, v ∈ 𝔼,

  • (3)

    d(u + v, w + e) ≤ d(u, w) + d(v, e), for all u, v, w, e ∈ 𝔼,

  • (4)

    (d, 𝔼) is a complete metric space.

Theorem 2 (see [32].)Let f(x) be a fuzzy-valued function on [a, ∞), and it is represented by . For any fixed r ∈ [0,1], assume that and are Riemann-integrable on [a, b] for every b ≥ a, and assume that there are two positive and such that and for every b ≥ a. Then f(x) is improper fuzzy Riemann-integrable on [a, ∞), and the improper fuzzy Riemann-integral is a fuzzy number. Furthermore, one has:

()

Definition 3. Let x, y ∈ 𝔼. If there exists z ∈ 𝔼 such that x = y + z, then z is called the H-difference of x and y, and it is denoted by x ⊖ y.

In this paper, the sign “⊖” always stands for H-difference, and also note that x ⊖ y ≠ x + (−1)y.

2.1. Caputo’s H-Differentiability

In this section, the concept of the fuzzy Caputo derivatives has been reviewed [33–35]. Also, we denote by C𝔽[a, b] a space of all fuzzy-valued functions which are continuous on [a, b]. Also, we denote the space of all Lebesgue integrable fuzzy-value functions on the bounded interval [a, b] ⊂ ℝ by L𝔽[a, b], and we denote the space of fuzzy-value functions f(x) which have continuous H-derivative up to order n − 1 on [a, b] such that f(n−1)(x) ∈ AC𝔽([a, b]) by AC(n)𝔽([a, b]).

Definition 4. Let f ∈ C𝔽[a, b]∩L𝔽[a, b]; the fuzzy Riemann-Liouville integral of fuzzy-valued function f is defined as follows:

()

Since , for all 0 ≤ r ≤ 1, then one can indicate the fuzzy Riemann-Liouville integral of fuzzy-valued function f based on the lower and upper functions as follows.

Theorem 5. Let f(x) ∈ C𝔽[a, b]∩L𝔽[a, b]; the fuzzy Riemann-Liouville integral of fuzzy-valued function f is defined by

()
where
()

Now, we define the fuzzy Riemann-Liouville fractional derivatives of order n − 1 < β < n for fuzzy-valued function f (which is a direct extension of strongly generalized H-differentiability [20] and lateral type of H-differentiability [36] in the fractional literature) as follows.

Definition 6. Let , let x0 ∈ (a, b), and let Φ(x) = (1//(x − t) β−n+1) (n = [β] + 1; x > a). We say that f is fuzzy Riemann-Liouville fractional differentiable of order β, at x0, if there exists an element , such that for all h > 0 sufficiently small

(i)
()
or
(ii)
()

For sake of simplicity, we say that a fuzzy-valued function f is  RL[(i) − β]-differentiable if it is differentiable as in Definition 6 case (i) and is  RL[(ii) − β]-differentiable if it is differentiable as in Definition 6 case (ii).

Theorem 7. Let f(x) ∈ C(n)𝔽[a, b]∩L𝔽[a, b], x0 ∈ (a, b), (β > 0), and (n = [β] + 1) such that for all 0 ≤ r ≤ 1, then

(i) if f(x) is a  RL[(i) − β]-differentiable fuzzy-valued function, then

()

(ii) if f(x) is a  RL[(ii) − β]-differentiable fuzzy-valued function, then

()
where
()

Definition 8. Let , and f(n) is integrable; then the right fuzzy Caputo derivative of f for n − 1 < β < n and x ∈ [a, b] is denoted by and defined by

()

Theorem 9. Let f(x) ∈ C(n)𝔽[a, b]∩L𝔽[a, b], x ∈ (a, b), and n − 1 < β < n, such that for all 0 ≤ r ≤ 1, then

(i) if f is a  C[(i) − β]-differentiable fuzzy-valued function, then

()

(ii) if f(x) is a  C[(ii) − β]-differentiable fuzzy-valued function, then

()
where
()

Proof. We prove the case of  C[(i) − β]-differentiability, (β) > 0, (n = [β] + 1), and for the case of  C[(ii) − β]-differentiability the proof is completely similar to previous one, and hence it is omitted.

Let us consider that f is  C[(i) − β]-differentiability and that x ∈ (a, b); then we have the following:

()
and multiplying by 1/h, we get the following:
()

Similarly, we get the following:  

()

Passing to the limit we obtain

()
which proves the theorem.

3. The Fuzzy Laplace Transforms

In this section, we consider the fuzzy Laplace transform for fuzzy-valued function; then derivative theorem is given which is essential to determine solutions of FFDEs.

In this way, Allahviranloo and Ahmadi [2] suggested the concept of Laplace transforms for fuzzy-valued function as follows.

Definition 10 (see [2].)Let f(x) be continuous fuzzy-value function. Suppose that f(x)⊙e−px is improper fuzzy Riemann-integrable on [0, ∞); then is called fuzzy Laplace transforms and is denoted by

()

Remark 11. In [8], the authors have investigated under what conditions the fuzzy-valued functions can possess the fuzzy Laplace transform. So, we suppose that the given fuzzy-valued functions have mentioned conditions throughout the paper.

From Theorem 2, we have
()
Also by using the definition of classical Laplace transform one has
()
then we get
()

Theorem 12 (see [2].)Let f(x), g(x) be continuous-fuzzy-valued functions; suppose that c1, c2 are constant; then

()

Lemma 13 (see [2].)Let f(x) be continuous fuzzy-value function on [0, ∞) and let λ ∈ ℝ; then

()

Lemma 14 (see [2].)Let f(x) be continuous fuzzy-value function and g(x) ≥ 0. Suppose that (f(x)⊙g(x))⊙e−px is improper fuzzy Riemann-integrable on [0, ∞); then

()

Theorem 15 (first translation theorem (see [2].)Let f be continuous fuzzy value function and let L[f(x)] = F(p). Then

()
where eax is real value function.

In order to solve FFDEs, it is necessary to know the fuzzy Laplace transform of Caputo’s H-derivative of f, . The virtue of is that it can be written in terms of L[f(x)].

Theorem 16 (derivative theorem). Suppose that f(x) ∈ C(n)𝔽[0, ∞)∩L𝔽[0, ∞); then

()
if D(k−1)f is  C[(i) − β]-differentiable, and also
()
if D(k−1)f is  C[(ii) − β]-differentiable.

Proof. For arbitrary fixed r ∈ [0,1] we have

()
Since D(k−1)f is   C[(i) − β], we get the following:
()
Hence, we get
()
Then, we obtained the following:
()
Then, we have
()
Using (32) leads to obtain
()
Now, we assume that D(k−1)f is the  C[(ii) − β]; then for arbitrary fixed r ∈ [0,1] we have
()
Since D(k−1)f is  C[(ii) − β], we get
()
and, hence, we get
()
So, we get
()
Thus, we obtain the following:
()
which completes the proof.

4. Fractional Green’s Functions

In the following, we present the so-called fundamental solutions of fractional Green’s functions for fuzzy fractional differential equations under Caputo’s H-differentiability. First we consider the nonhomogeneous fuzzy fractional differential equation of order 0 < β < 1 together with nonhomogeneous initial condition
()
where t > 0. Fractional Green’s functions for case so-called the classical Green’s functions, that is, considering φ(x) = δ(x) and , are discussed.

4.1. Determining Algebraic Solutions

The algebraic solutions of fuzzy fractional differential equations have been investigated under Caputo’s H-differentiability. We provided the fuzzy Laplace transform to obtain the solutions of FFDE (42). By taking Laplace transform on the both sides of (42), we get
()
After that, based on the types of Caputo’s H-differentiability we have the following cases.

Case I. Let us consider that DΦ(x) is a  C[(i) − β]-differentiable function; then (43) is extended based on the its lower and upper functions as follows:

()
where
()
In order to solve the linear system (44), for simplify we assume that
()
where H1(p; r) and K1(p; r) are solutions of system (44). Then, by using the inverse Laplace transform, and are computed as follows:
()
To explicit the corresponding Green’s function, which is solution of the above relation satisfying the condition and taking φ(x) = δ(x), we use the linearity of the inverse Laplace transform to obtain
()

Case II. Let us consider that DΦ(x) is  C[(ii) − β]-differentiable; then (43) can be written as follows:

()
where
()
Consequently, to solve the linear system (49), we set for simplify
()
where H2(p; r) and K2(p; r) are solutions of system (49). Then by making use of the inverse Laplace transform, and are computed as follows:
()
To show the corresponding Green’s function, which is solution of (42) satisfying the condition and taking φ(x) = δ(x), we use the linearity of the inverse Laplace transform to obtain
()

5. Examples

In this section, we consider several examples, and we find explicit expressions for fractional Green’s functions, including some versions of the fuzzy harmonic oscillator equations and fuzzy relaxation equation under Caputo’s H-differentiability.

Example 1 (Green’s function for fuzzy damped harmonic oscillator). Let us examine the following FFDE:

()
where a, b are real positive constants and w is the frequency of the harmonic oscillator. We will solve this example according to the two following cases for λ ∈ ℝ.

Case I. Suppose that λ ∈ ℝ+ = (0, ∞); then taking Laplace transform on the both sides of above equation, we have

()
Using  C[(i) − β]-differentiability, we get
()
Then, after some calculations, we obtain the following:
()
Consequently, taking the inverse of Laplace on both sides of (57) we have
()
Finally, we determine the solution of FFDE as follows:
()
To explicit the corresponding Green’s function under  C[(i) − β]-differentiability, which is solution of (54) satisfying the condition and taking φ(x) = δ(x), we use the linearity of the inverse Laplace transform to obtain
()
On the other hand, taking , we have a homogeneous fuzzy fractional differential equation whose solution under  C[(i) − β]-H-differentiability is given by
()

Case II. If λ ∈ ℝ− = (−∞, 0), then by using  C[(ii) − β]-differentiability and Theorem 16, and their inverses, fractional Green’s function will be obtained similar to (60).

Example 2 (Green’s function for fuzzy the driven harmonic oscillator). Let us investigate the following FFDEs; namely,

()

with b = 0 and 1/2 < β < 1; the fuzzy fractional differential equation associated with the driven harmonic oscillator is obtained. We obtain the same result taking b = 0, a = 1 and solve this example according to the two following cases for λ ∈ ℝ.

Case I. Suppose that λ ∈ ℝ+ = (0, +∞); then taking Laplace transform on the both sides of above equation, we have the following:

()
Using  C[(i) − β]-differentiability, we obtain
()
Then, after some manipulations the following result is reported:
()
By taking inverse of Laplace on the both sides of (75) we have
()
Finally, we determine the solution of FFDE as follows:
()
To show the corresponding Green’s function under  C[(i) − β]-differentiability, which is solution of (62) satisfying the condition and taking φ(x) = δ(x), we use the linearity of the inverse Laplace transform to obtain
()
In the case β = 1, we report
()
which is the classic Green’s function associated with fuzzy the driven harmonic oscillator.

Taking , we have a homogeneous fuzzy fractional differential equation whose solution under  C[(i) − β]-H-differentiability is given by
()
For β = 1, we get
()

Case II. Let us suppose that λ ∈ ℝ− = (−∞, 0); then using  C[(ii) − β]-differentiability and Theorem 16 and their inverses, fractional Green’s function will be obtained similar to (68).

Example 3 (Green’s functions for fuzzy fractional relaxation equation). The next step is to consider the following FFDE:

()
where a = 0 in (54) and 0 < β < 1. We solve this example according to the two following cases corresponding to λ ∈ ℝ.

Case I. Suppose that λ ∈ ℝ+ = (0, +∞); then taking Laplace transform on the both sides of above equation, we have

()
Using  C[(i) − β]-differentiability, we get
()
Then, after some manipulations we get the following:
()
By taking inverse of Laplace on the both sides of (75) we have
()
Thus, we determine the solution of FFDE as follows:
()
Here, we obtain explicitly Green’s functions under  C[(i) − β]-differentiability, introducing φ(x) = δ(x) and ; that is,
()
When β = 1, we get the classic Green’s function under strongly generalized differentiability
()
On the other hand, taking , we have a homogeneous fuzzy fractional differential equation whose solution under  C[(i) − β]-H-differentiability is given by
()
Finally, in the case β = 1 we get
()

Case II. Suppose that λ ∈ ℝ− = (−∞, 0); then using  C[(ii) − β]-differentiability and Theorem 16, and their inverses, fractional Green’s function will be obtained similar to (78).

Now, we provide some examples such that the obtained solutions coincide with the previously reported solution in integer case [37].

Example 4. For a special case, let us consider the following FFDE:

()
where y represents the number of radionuclides present in a given radioactive and λ is a decay constant.

Case I. Suppose that λ ∈ ℝ+ = (0, +∞); then using  C[(i) − β]-differentiability and Theorem 16, the solution is derived as follows:

()

Case II. Suppose that λ ∈ ℝ− = (−∞, 0); then using  C[(ii) − β]-differentiability and Theorem 16, the solution will be obtained similar to (83). For more details see Figures 1, 2, 3, and 4.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Solution of Example 4, Case I, β = 1.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Solution of Example 4, Case I, β = 0.5.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Solution of Example 4, Case II, β = 1.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Solution of Example 4, Case II, β = 0.5.

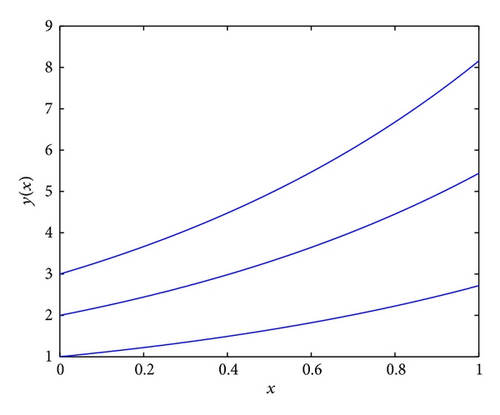
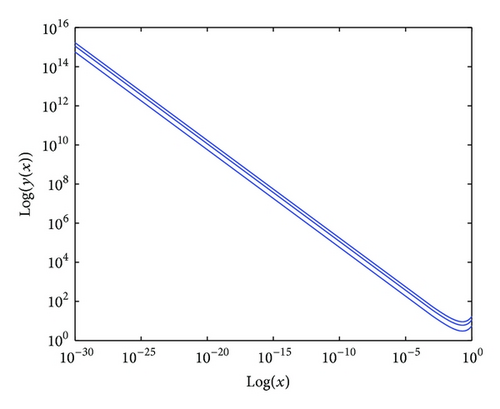
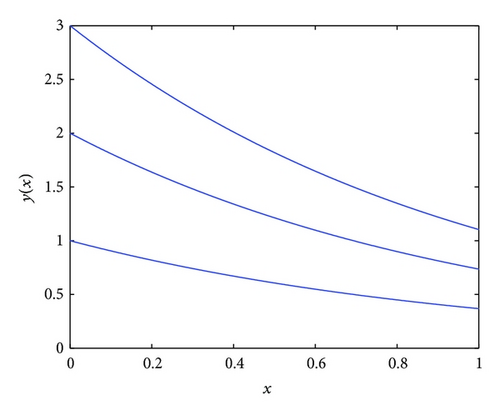
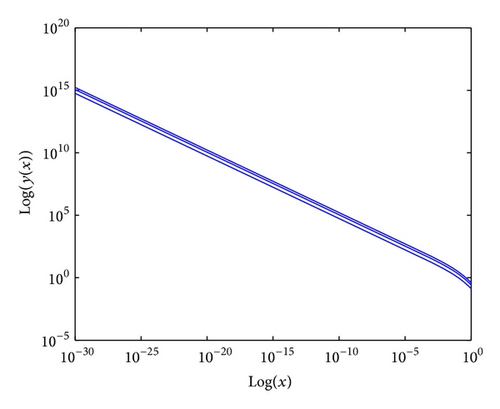
Example 5. Let us discuss the following FFDE:

()
Then, using  C[(ii) − β]-differentiability and Theorem 16, the solution becomes as follows:
()
For more details see Figures 5 and 6.

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
Solution of Example 5, β = 1.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
Solution of Example 5, β = 0.5.

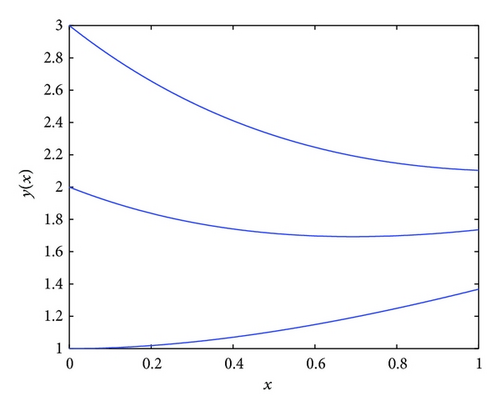
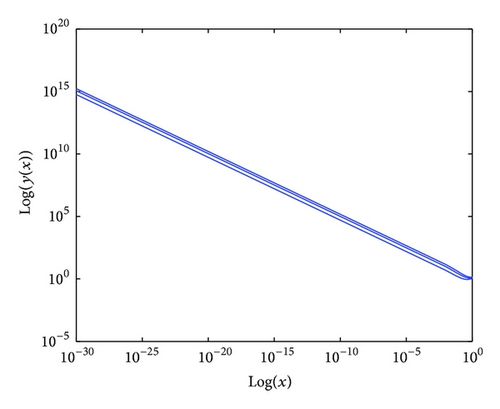
6. Conclusion

In this paper, the fractional Green’s functions for the solutions of FFDEs by using the fuzzy Laplace transforms under Caputo’s differentiability were applied. Some particular cases were also presented, involving some fuzzy versions of the harmonic oscillator. To this end, some needed concepts are given like the Caputo derivatives, fuzzy Laplace transforms, and their inverses, and so forth. For future research, we extend the boundary value problem for FDE [38] to the fractional case.

Acknowledgments

The authors thank the referees for careful reading and helpful suggestions on the improvement of the paper.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.