We investigate synchronization between two discrete-time networks with mutual couplings, including inner synchronization inside each network and outer synchronization between two networks. We then obtain a synchronized criterion for the inner synchronization inside each network by the method of linear matrix inequality and derive a relationship between the inner and outer synchronization. Finally, we show numerical examples to verify our theoretical analysis and discuss the effect of coupling strengths, node dynamics, and topological structures on the inner and outer synchronization. Compared to the inner synchronization inside each network, the outer synchronization between two networks is difficult to achieve.

1. Introduction

Network synchronization, as a collective behavior existing inside a network, has been widely studied since the birth of small-world and scale-free networks [1–3]. The main focus is to investigate the interplay between the complexity in the overall topology and the local dynamics of the coupled nodes [4–6]. The topological structures may be globally connected, random, small-world, and scale-free. There are many applications using the synchronization of networks [7], for instance, secure communication and multirobot coordination control. Apart from the complete synchronization appearing inside a network, there are some other types of synchronization, such as phase synchronization, generalized synchronization, lag synchronization, and cluster synchronization [8–12].

Generally, we refer to synchronization happening between two networks as outer synchronization [13], which is distinguished from inner synchronization inside a network. Compared to the inner synchronization, outer synchronization of two networks is more complex, which involves more system parameters. In 2007, Li et al. first proposed the concept of outer synchronization and applied the open-plus-closed-loop method to realize the outer synchronization between two networks with identical topologies [13]. Shortly later, using the adaptive control method, Tang et al. achieved the outer synchronization between two networks with different topological structures [14]. In [15], Wu et al. studied the generalized outer synchronization between two networks with different dimensions of node dynamics. In addition, there are many works on the outer synchronization, that is, introducing the noise, time delay, fractional order node dynamics, and unknown parameters [16–21].

In the above-mentioned works on the outer synchronization, the researchers usually applied the control methods to realize the outer synchronization and did not study the inner synchronization inside a network. In reality, the mutual coupling forms between two networks are colorful; for instance, Wu et al. investigated the outer synchronization between two networks with two active forms nonlinear signals and reciprocity [22]; however, these two coupling forms do not make the outer synchronization happen. In addition, the inner synchronization inside each network was not considered. In [23], Sorrentino and Ott provided a method to study the inner synchronization of two groups. The problem of collective behaviors inside a network and between two networks is of broad interest. For example, in subway systems, when the trains reach the platform, the outer and inner doors simultaneously open or close, showing that both inner and outer synchronization happen [24]. It is also found that present studies on the synchronization between two networks with various couplings are much less, then studying the effect of various couplings on the synchronization is interesting and meaningful.

Inspired by the above discussions, we study synchronization between two discrete-time networks with mutual couplings, including inner synchronization inside each network and outer synchronization between them. By the Lyapunov stability theory and linear matrix inequality, we obtain a synchronous theorem on the inner synchronization inside each network and a relationship between the inner and outer synchronization. Numerical simulations show that the inner synchronization is easier to achieve than the outer synchronization. In addition, given the mutual coupling matrices and appropriate node dynamics, we can adjust coupling strengths to realize the inner and outer synchronization simultaneously. In Section 2, network models and synchronization analysis are presented, and numerical examples are shown in Section 3. Finally, the discussions are included in the last section.

2. Model Presentation and Synchronization Analysis

In this paper, we investigate the synchronization between two discrete-time networks with mutual couplings. The dynamical equations are described as follows:

()

where the node dynamical equations are x_i(t + 1) = f(x_i(t)) and y_i(t + 1) = g(y_i(t)), i = 1, …, N. f(·) : Rⁿ → Rⁿ and g(·) : Rⁿ → Rⁿ are continuously differential functions. x_i(y_i) is an n-dimensional state vector. N is the number of network nodes. m_x and m_y are the coupling strengths. A = (a_ij) _N×N and B = (b_ij) _N×N represent the mutual coupling matrices between these two networks, whose entries a_ij denote the intensity from i in network X to j in network Y; analogously, the entries of B are the same defined as A.

Let us now consider the possibility whether the individual networks achieve inner synchronization; that is, lim _t→+∞ ∥x_i(t) − x_s(t)∥ = 0 and lim _t→+∞∥y_i(t) − y_s(t)∥ = 0, i = 1 … , N, where ∥·∥ denotes the Euclidean norm of a vector. If there exist such synchronous states, satisfying

()

without loss of generality, we set γ_x = γ_y = 1.

Thus the synchronized state equations are

()

Linearizing the synchronous states around x_s and y_s, we obtain

()

where δx_i(t) = x_i(t) − x_s(t), δy_i(t) = y_i(t) − y_s(t), Df(x_s(t)), and Dg(y_s(t)) are the Jacobians of f(x(t)), g(y(t)) at x_s and y_s, respectively. Assume A = B and let δx(t) = [δx₁(t), …, δx_N(t)] ∈ R^n×N and δy(t) = [δy₁(t), …, δy_N(t)] ∈ R^n×N. Then (4) is rewritten as

()

Further, let

; then (5) reads

()

where

and

, where I_n is an identity matrix of size n and A^T denotes the transpose of A. Generally, the coupling matrix can be decomposed into A^T = ΦJΦ⁻¹, where J is the Jordan canonical form with complex eigenvalues λ ∈ C and Φ contains the corresponding eigenvectors ϕ. Denote η(t) = δ(t)Φ; we obtain

()

where J is a block diagonal matrix; that is,

()

and J_k is the block corresponding to the N_k multiple eigenvalue λ_k of A^T; that is,

()

Let η(t) = [η₁(t), η₂(t), …, η_h(t)] and

. We can rewrite (7) in a component form as

()

where k = 1,2, …, h.

Firstly, we study the system of (10). Let η_k,1(t) = μ_k,1(t) + jν_k,1(t), λ_k = α_k + jβ_k, where α_k, β_k ∈ R, μ_k,1, ν_k,1 ∈ R²ⁿ, j is and the imaginary unit. Then (10) reads

()

Construct the Lyapunov function as

()

Then,

()

where

with

. If M_k < 0, k = 1,2, …, h, that is, these matrices are negative definite, then the zero solution of (10) is asymptotically stable.

Secondly, we study the stability of (11). Let η_k,p+1(t) = μ_k,p+1(t) + jν_k,p+1(t); then

()

Choose the Lyapunov function as

()

Then we obtain

()

where

with

()

If L_k < 0, k = 1,2, …, h, then the zero solution of (11) is asymptotically stable. Hence we obtain a synchronized theorem for networks (1).

Theorem 1. Consider network systems (1). Assume the mutual coupling matrices A = B. Let λ_k = α_k + jβ_k be the eigenvalues of A, where α_k, β_k ∈ R. If these matrices M_k, L_k < 0, k = 1,2, …, h, then the networks (1) will achieve inner synchronization inside each network.

Remark 2. Note that Theorem 1 only gives a feasibility of the inner synchronization inside each network. When the inner synchronization inside networks X and Y happens, and the synchronized states ∥x_s(t) − y_s(t)∥ → 0 for a large time, then the outer synchronization between networks X and Y will be achieved.

3. Numerical Examples

In this section, we will give some examples to illustrate our theoretical results obtained in the previous section. We mainly investigate the effect of coupling strengths, node dynamics, and mutual coupling forms on the inner and outer synchronization. We consider the following coupled discrete-time networks, which are in the form of (1):

()

where the node equations in (19) are both Henön maps, which have colorful dynamical properties, for instance, a₁ = 0.5 and b₁ = 0.3; it has a periodic solution. Since the sum of each row of mutual matrices is one, for simplicity, we take a_ij = b_ij = 1/N for i, j = 1, …, N. To measure the extent to which inner synchronization is achieved, we introduce two quantities, E_x = ∥x_i(t) − x_s(t)∥ and E_y = ∥y_i(t) − y_s(t)∥, i = 1, …, N. In addition, we denote another quantity E_outer = ∥x_i(t) − y_i(t)∥ for i = 1, …, N to demonstrate whether outer synchronization happens. Given the values of a₁ = 0.3, b₁ = 0.2, a₂ = 0.5, and b₂ = 0.3, we first study the effect of coupling strengths m_x and m_y on the inner and outer synchronization. Figure 1 shows that the outer synchronization does not happen when the coupling strength is m_x < 0.5, while the inner synchronization inside network X always appears. In the same way, considering the effect of coupling strength m_y, the details are shown in Figure 2.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

The panels exhibit E_x, E_y, and E_outer at t = 400 with regard to m_x for N = 10 and m_y = 0.2. The bottom one shows that the inner synchronization inside network X is easily achieved. When m_x ≥ 0.5, the inner and outer synchronization simultaneously appear.

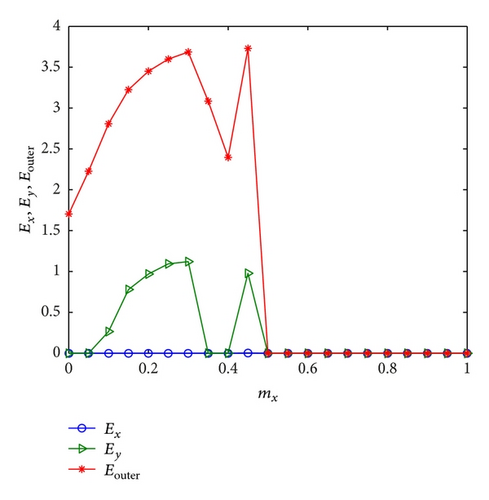
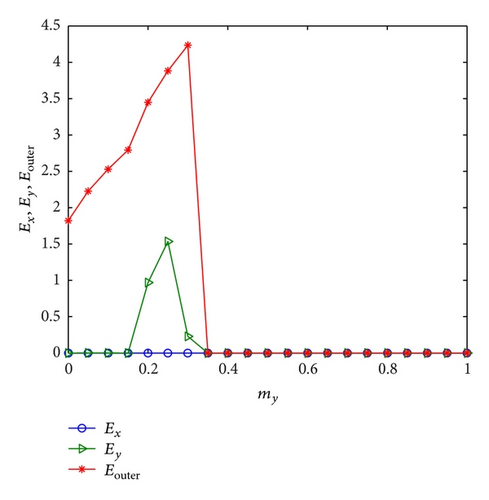
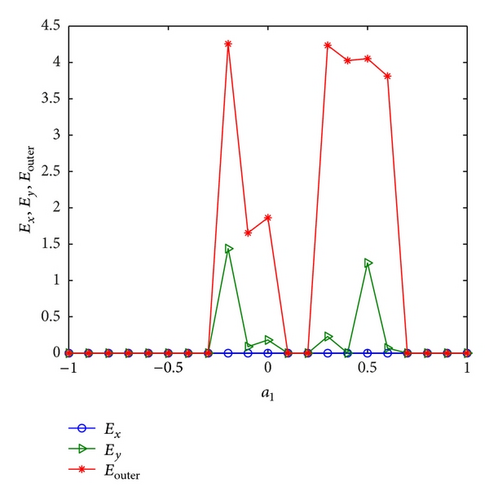
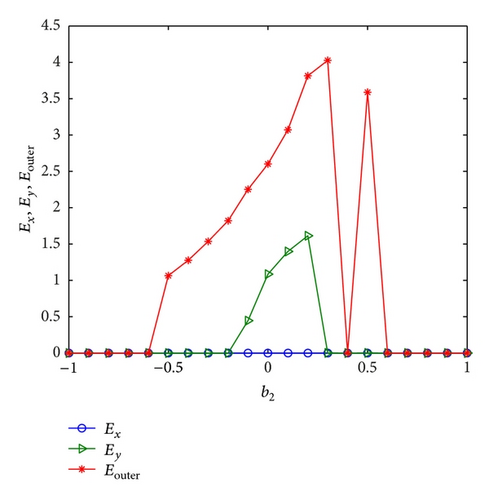
Next, we discuss the effect of node dynamics on the inner and outer synchronization and take b₁ = 0.2, a₂ = 0.5, and b₂ = 0.3 and N = 10, m_x = 0.2, and m_y = 0.3. We then investigate the effect of parameter a₁ on the inner and outer synchronization. Similarly, given a₁ = 0.3, b₁ = 0.2, and a₂ = 0.5 and N = 10, m_x = 0.2, and m_y = 0.3, we study the influence of b₂. The numerical simulations are summarized in Figures 3 and 4, showing that the inner synchronization inside network X always happens, while the inner synchronization inside network Y and the outer synchronization only appear for some values of a₁ or b₂.

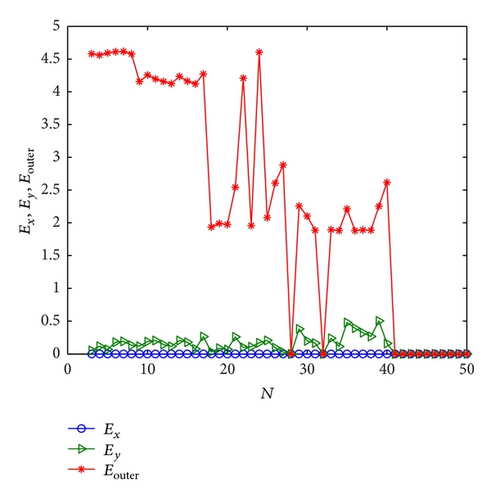
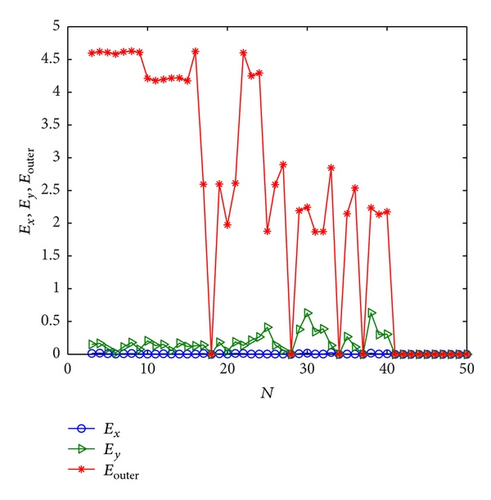
Finally, we discuss the effect of network size N on the inner and outer synchronization with a_ij = b_ij = 1/N, i, j = 1, …, N. Taking the values of a₁ = 0.3, b₁ = 0.2, a₂ = 0.5, and b₂ = 0.3 and m_x = 0.2 and m_y = 0.3, we plot the curves of E_x, E_y, and E_outer in Figure 5. In the following, we change the topological structures of mutual coupling matrices and choose A = B as a random matrix; the numerics are shown in Figure 6. It is found that the globally connected and random topological structures have similar effect on the inner and outer synchronization. It is noted that the inner synchronization inside network X always happens. A possible reason is the effect of node dynamics. Furthermore, when the Henön map behaves chaotically, no synchronization appears.

4. Conclusions

The current study investigated the synchronization between two discrete-time networks with mutual couplings and mainly studied inner synchronization inside each network and outer synchronization between them. We then obtained a synchronous theorem on the inner synchronization inside each network in terms of linear matrix inequality, for the lack of a criterion on the outer synchronization. When the inner synchronization is achieved inside each network and the synchronized states x_s and y_s are same for a large time, then the outer synchronization will happen. From the numerical simulations, we see that the inner and outer synchronization simultaneously happen when we adjust the values of coupling strengths and parameters in the node dynamics. The globally connected and random topologies have similar effect on the inner and outer synchronization. In addition, outer synchronization is more difficult to achieve than the inner synchronization, meaning that the outer synchronization needs a strong coupling form. Because of the diversity of coupling forms between two networks, deriving the criteria on the inner and outer synchronization simultaneously is a technical challenge, which would be discussed in the future.

Conflict of Interests

The authors declare that there is no conflict of interests regarding the publication of this paper.

Acknowledgments

This work was supported by the National Natural Science Foundation of China (nos. 61203155 and 11171084) and Zhejiang Provincial Natural Science Foundation of China under Grant no. LQ12F03003.

References

1 Watts D. J. and Strogatz S. H., Collective dynamics of small-world networks, Nature. (1998) 393, no. 6684, 440–442, 2-s2.0-0032482432.
10.1038/30918
CAS PubMed Web of Science® Google Scholar
2 Barabási A.-L. and Albert R., Emergence of scaling in random networks, Science. (1999) 286, no. 5439, 509–512, https://doi.org/10.1126/science.286.5439.509, MR2091634, ZBL1226.05223.
10.1126/science.286.5439.509
CAS PubMed Web of Science® Google Scholar
3 Boccaletti S., Latora V., Moreno Y., Chavez M., and Hwang D.-U., Complex networks: structure and dynamics, Physics Reports. (2006) 424, no. 4-5, 175–308, https://doi.org/10.1016/j.physrep.2005.10.009, MR2193621.
10.1016/j.physrep.2005.10.009
Web of Science® Google Scholar
4 Arenas A., Díaz-Guilera A., Kurths J., Moreno Y., and Zhou C., Synchronization in complex networks, Physics Reports. (2008) 469, no. 3, 93–153, https://doi.org/10.1016/j.physrep.2008.09.002, MR2477097.
10.1016/j.physrep.2008.09.002
Web of Science® Google Scholar
5 Wang Q., Duan Z., Chen G., and Feng Z., Synchronization in a class of weighted complex networks with coupling delays, Physica A. (2008) 387, no. 22, 5616–5622, 2-s2.0-47649084753, https://doi.org/10.1016/j.physa.2008.05.056.
10.1016/j.physa.2008.05.056
Web of Science® Google Scholar
6 Yu W., Chen G., Lü J., and Kurths J., Synchronization via pinning control on general complex networks, SIAM Journal on Control and Optimization. (2013) 51, no. 2, 1395–1416, https://doi.org/10.1137/100781699, MR3038018, ZBL1266.93071.
10.1137/100781699
Web of Science® Google Scholar
7 Sheikhan M., Shahnazi R., and Garoucy S., Synchronization of general chaotic systems using neural controllers with application to secure communication, Neural Computing and Applications. (2013) 22, no. 2, 361–373.
10.1007/s00521-011-0697-0
Web of Science® Google Scholar
8 Li X., Phase synchronization in complex networks with decayed long-range interactions, Physica D. (2006) 223, no. 2, 242–247, 2-s2.0-33750462780, https://doi.org/10.1016/j.physd.2006.09.026.
10.1016/j.physd.2006.09.026
Web of Science® Google Scholar
9 Sun M., Zeng C., and Tian L., Linear generalized synchronization between two complex networks, Communications in Nonlinear Science and Numerical Simulation. (2010) 15, no. 8, 2162–2167, https://doi.org/10.1016/j.cnsns.2009.08.010, MR2592629, ZBL1222.93088.
10.1016/j.cnsns.2009.08.010
Web of Science® Google Scholar
10 Ji D. H., Jeong S. C., Park J. H., Lee S. M., and Won S. C., Adaptive lag synchronization for uncertain complex dynamical network with delayed coupling, Applied Mathematics and Computation. (2012) 218, no. 9, 4872–4880, https://doi.org/10.1016/j.amc.2011.10.051, MR2870012, ZBL1238.93053.
10.1016/j.amc.2011.10.051
Web of Science® Google Scholar
11 Lu W. L., Liu B., and Chen T., Cluster synchronization in networks of distinct groups of maps, European Physical Journal B. (2010) 77, no. 2, 257–264, 2-s2.0-78149285407, https://doi.org/10.1140/epjb/e2010-00202-7.
10.1140/epjb/e2010-00202-7
CAS Web of Science® Google Scholar
12 Ma Z., Liu Z., and Zhang G., A new method to realize cluster synchronization in connected chaotic networks, Chaos. (2006) 16, no. 2, 023103, https://doi.org/10.1063/1.2184948, MR2243805, ZBL1146.37330.
10.1063/1.2184948
PubMed Web of Science® Google Scholar
13 Li C., Sun W., and Kurths J., Synchronization between two coupled complex networks, Physical Review E. (2007) 76, no. 4, 2-s2.0-35248825562, https://doi.org/10.1103/PhysRevE.76.046204, 046204.
10.1103/PhysRevE.76.046204
CAS PubMed Web of Science® Google Scholar
14 Tang H., Chen L., Lu J.-A., and Tse C. K., Adaptive synchronization between two complex networks with nonidentical topological structures, Physica A. (2008) 387, no. 22, 5623–5630, 2-s2.0-47649131867, https://doi.org/10.1016/j.physa.2008.05.047.
10.1016/j.physa.2008.05.047
Web of Science® Google Scholar
15 Wu X., Zheng W. X., and Zhou J., Generalized outer synchronization between complex dynamical networks, Chaos. (2009) 19, no. 1, 013109, https://doi.org/10.1063/1.3072787, MR2513757.
10.1063/1.3072787
PubMed Web of Science® Google Scholar
16 Wang G., Cao J., and Lu J., Outer synchronization between two nonidentical networks with circumstance noise, Physica A. (2010) 389, no. 7, 1480–1488, 2-s2.0-73449145071, https://doi.org/10.1016/j.physa.2009.12.014.
10.1016/j.physa.2009.12.014
CAS Web of Science® Google Scholar
17 Sun Y. Z. and Zhao D. H., Effects of noise on the outer synchronization of two unidirectionally coupled complex dynamical networks, Chaos. (2012) 22, no. 2, 023131.
10.1063/1.4721997
PubMed Web of Science® Google Scholar
18 Zheng S., Wang S., Dong G., and Bi Q., Adaptive synchronization of two nonlinearly coupled complex dynamical networks with delayed coupling, Communications in Nonlinear Science and Numerical Simulation. (2012) 17, no. 1, 284–291, https://doi.org/10.1016/j.cnsns.2010.11.029, MR2826007, ZBL1239.93060.
10.1016/j.cnsns.2010.11.029
Web of Science® Google Scholar
19 Asheghan M. M., Míguez J., Hamidi-Beheshti M. T., and Tavazoei M. S., Robust outer synchronization between two complex networks with fractional order dynamics, Chaos. (2011) 21, no. 3, 2-s2.0-80053433381, https://doi.org/10.1063/1.3629986, 033121.
10.1063/1.3629986
PubMed Web of Science® Google Scholar
20 Wu Z. and Fu X., Outer synchronization between drive-response networks with nonidentical nodes and unknown parameters, Nonlinear Dynamics. (2012) 69, no. 1-2, 685–692, https://doi.org/10.1007/s11071-011-0296-8, MR2929902, ZBL1258.34131.
10.1007/s11071-011-0296-8
Web of Science® Google Scholar
21 Wu X. and Lu H., Outer synchronization of uncertain general complex delayed networks with adaptive coupling, Neurocomputing. (2012) 82, 157–166, 2-s2.0-84856426678, https://doi.org/10.1016/j.neucom.2011.10.022.
10.1016/j.neucom.2011.10.022
Web of Science® Google Scholar
22 Wu Y.-Q., Sun W.-G., and Li S.-S., Anti-synchronization between coupled networks with two active forms, Communications in Theoretical Physics. (2011) 55, no. 5, 835–840, 2-s2.0-79957959980, https://doi.org/10.1088/0253-6102/55/5/19.
10.1088/0253-6102/55/5/19
Web of Science® Google Scholar
23 Sorrentino F. and Ott E., Network synchronization of groups, Physical Review E. (2007) 76, no. 5, 056114, https://doi.org/10.1103/PhysRevE.76.056114, MR2495364.
10.1103/PhysRevE.76.056114
Web of Science® Google Scholar
24 Sun W., Zhang J., and Li C., Synchronization analysis of two coupled complex networks with time delays, Discrete Dynamics in Nature and Society. (2011) 2011, 12, 209321, https://doi.org/10.1155/2011/209321, MR2800601, ZBL1259.34074.
10.1155/2011/209321
Web of Science® Google Scholar

Citing Literature

All articles

Synchronization between Two Discrete-Time Networks with Mutual Couplings

Abstract

1. Introduction

2. Model Presentation and Synchronization Analysis

3. Numerical Examples

4. Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Synchronization between Two Discrete-Time Networks with Mutual Couplings

Abstract

1. Introduction

2. Model Presentation and Synchronization Analysis

3. Numerical Examples

4. Conclusions

Conflict of Interests

Acknowledgments

References

Citing Literature

Figures

References

Related

Information