State-Feedback Stabilization for a Class of Stochastic Feedforward Nonlinear Time-Delay Systems
Abstract
We investigate the state-feedback stabilization problem for a class of stochastic feedforward nonlinear time-delay systems. By using the homogeneous domination approach and choosing an appropriate Lyapunov-Krasovskii functional, the delay-independent state-feedback controller is explicitly constructed such that the closed-loop system is globally asymptotically stable in probability. A simulation example is provided to demonstrate the effectiveness of the proposed design method.
1. Introduction
Feedforward (also called upper-triangular) system is another important class of nonlinear systems. Firstly, from a theoretical point of view, since they are not feedback linearizable and maybe not stabilized by applying the conventional backstepping method, the stabilization problem of these systems is more difficult than that of lower-triangular systems. Secondly, many physical devices, such as the cart-pendulum system in [20] and the ball-beam system with a friction term in [21], can be described by equations with the feedforward structure. In the recent papers, the stabilization problems for feedforward nonlinear (or time-delay) systems have achieved remarkable development; see, for example, [22–29] and the references therein.
However, all these above-mentioned results are limited to deterministic systems. There are fewer results on stochastic feedforward nonlinear systems until now, due to the special characteristics of this system. To the best of the authors’ knowledge, [30] is the only paper to consider this kind of stochastic feedforward nonlinear systems, but the assumptions on the nonlinearities are restrictive.
The purpose of this paper is to further weaken the assumptions on the drift and diffusion terms of system (1) and solve the state-feedback stabilization problem. By using the homogeneous domination approach in [26] and choosing an appropriate Lyapunov-Krasovskii functional, a delay-independent state-feedback controller is explicitly constructed such that the closed-loop system is globally asymptotically stable in probability.
The paper is organized as follows. Section 2 provides some preliminary results. The design and analysis of state-feedback controller are given in Sections 3 and 4, respectively, following a simulation example in Section 5. Section 6 concludes this paper.
2. Preliminary Results
The following notations, definitions, and lemmas are to be used throughout the paper.
R+ denotes the set of all nonnegative real numbers, and Rn denotes the real n-dimensional space. For a given vector or matrix X, XT denotes its transpose, Tr {X} denotes its trace when X is square, and |X| is the Euclidean norm of a vector X. 𝒞([−d, 0]; Rn) denotes the space of continuous Rn-value functions on [−d, 0] endowed with the norm ∥·∥ defined by ∥f∥ = sup x∈[−d,0]|f(x)| for f ∈ 𝒞([−d, 0]; Rn); denotes the family of all ℱ0-measurable bounded 𝒞([−d, 0]; Rn)-valued random variables ξ = {ξ(θ):−d ≤ θ ≤ 0}. 𝒞i denotes the set of all functions with continuous ith partial derivatives; 𝒞2,1(Rn × [−d, ∞); R+) denotes the family of all nonnegative functions V(x, t) on Rn × [−d, ∞) which are 𝒞2 in x and 𝒞1 in t; 𝒞2,1 denotes the family of all functions which are 𝒞2 in the first argument and 𝒞1 in the second argument. 𝒦 denotes the set of all functions R+ → R+, which are continuous, strictly increasing, and vanishing at zero; 𝒦∞ denotes the set of all functions which are of class 𝒦 and unbounded; 𝒦ℒ is the set of all functions β(s, t): R+ × R+ → R+, which are of 𝒦 for each fixed t and decrease to zero as t → ∞ for each fixed s.
Definition 1 (see [6].)For any given V(x(t), t) ∈ 𝒞2,1 associated with system (2), the differential operator ℒ is defined as
Definition 2 (see [6].)The equilibrium x(t) = 0 of system (2) is said to be globally asymptotically stable (GAS) in probability if for any ϵ > 0 there exists a function β(·, ·) ∈ 𝒦ℒ such that P{|x(t)| ≤ β(∥ξ∥, t)} ≥ 1 − ϵ for any t ≥ 0, , where ∥ξ∥ = sup θ∈[−d,0]|x(θ)|.
Definition 3 (see [26].)For fixed coordinates (x1, …, xn) T ∈ Rn and real numbers ri > 0, i = 1, …, n, one has the following.
- (i)
The dilation Δɛ(x) is defined by for any ɛ > 0; r1, …, rn are called as the weights of the coordinates. For simplicity, we define dilation weight Δ = (r1, …, rn).
- (ii)
A function V ∈ 𝒞(Rn, R) is said to be homogeneous of degree τ if there is a real number τ ∈ R such that V(Δɛ(x)) = ɛτV(x1, …, xn) for any x ∈ Rn∖{0}, ɛ > 0.
- (iii)
A vector field h ∈ 𝒞(Rn, Rn) is said to be homogeneous of degree τ if there is a real number τ ∈ R such that for any x ∈ Rn∖{0}, ɛ > 0, i = 1, …, n.
- (iv)
A homogeneous p-norm is defined as for any x ∈ Rn, where p ≥ 1 is a constant. For simplicity, in this paper, one chooses p = 2 and writes ∥x∥Δ for ∥x∥Δ,2.
Lemma 4 (see [6].)For system (2), if there exist a function V(x(t), t) ∈ 𝒞2,1(Rn × [−d, ∞); R+), two class 𝒦∞ functions α1, α2, and a class 𝒦 function α3 such that
Lemma 5 (see [26].)Given a dilation weight Δ = (r1, …, rn), suppose that V1(x) and V2(x) are homogeneous functions of degrees τ1 and τ2, respectively. Then V1(x)V2(x) is also homogeneous with respect to the same dilation weight Δ. Moreover, the homogeneous degree of V1 · V2 is τ1 + τ2.
Lemma 6 (see [26].)Suppose that V : Rn → R is a homogeneous function of degree τ with respect to the dilation weight Δ; then (i) ∂V/∂xi is homogeneous of degree τ − ri with ri being the homogeneous weight of xi; (ii) there is a constant c such that . Moreover, if V(x) is positive definite, then , where is a positive constant.
Lemma 7 (see [5].)Let c and d be positive constants. For any positive number , then |x|c|y|d≤.
3. Design of State-Feedback Controller
The objective of this paper is to design a state-feedback controller for system (1) such that the equilibrium of the closed-loop system is globally asymptotically stable in probability.
3.1. Assumptions
For system (1), we need the following assumptions.
Assumption 8. For i = 1, …, n − 1, there exist positive constants a1 and a2 such that
Assumption 9. The time-varying delay d(t) satisfies for a constant γ.
Remark 10. When xi+1 = xi+1(t − d(t)) = 0 in diffusion term gi (i = 1, …, n − 1), Assumption 8 reduces to the same form as in [30], from which one can see that system (1) is more general than [30]. The significance and reasonability of Assumption 8 are illustrated in that paper.
Firstly, we introduce the following coordinate transformation:
3.2. State-Feedback Controller Design
We construct a state-feedback controller for system (7).
Step 1. Introducing ξ1 = η1 and choosing , from (3) and (7), it follows that
The first virtual controller
Step i (i = 2, …, n). In this step, we can get the following lemma.
Lemma 11. Suppose that at step i − 1, there is a set of virtual controllers defined by
Proof. See the Appendix.
4. Stability Analysis
We state the main result in this paper.
Theorem 12. If Assumptions 8 and 9 hold for the stochastic feedforward nonlinear time-delay system (1), under the state-feedback controller u = κnv and (13), then
- (i)
the closed-loop system has a unique solution on [−d, ∞);
- (ii)
the equilibrium at the origin of the closed-loop system is GAS in probability.
Proof. We prove Theorem 12 by four steps.
Step 1. Since fi, gi, i = 1, …, n, are assumed to be locally Lipschitz, so the system consisting of (13) and (15) satisfies the locally Lipschitz condition.
Step 2. We consider the following entire Lyapunov function for system (15):
By Lemma 4.3 in [31] and Lemma 6, there exist positive constants and , class 𝒦∞ functions and , and a positive definite function U(η) whose homogeneous degree is 4 such that
From d(t) : R+ → [0, d] and (19), it follows that
Step 3. By Lemma 6 and (14), there exists a positive constant c01 such that
By Assumption 8, (6), and 0 < κ < 1, one has
Since c01 is a constant independent of c02, c03, , , and γ, by choosing
Equation (27) becomes , where c0 is a positive constant. By (19), one obtains
By Steps 1–3 and Lemma 4, the system consisting of (13) and (15) has a unique solution on [−d, ∞), η = 0 is GAS in probability, and P{lim t→∞|η| = 0} = 1.
Step 4. Since (6) is an equivalent transformation, so the closed-loop system consisting of (1), u = κnv, and (13) has the same properties as the system (13) and (15). Theorem 12 holds.
Remark 13. In this paper, the homogeneous domination idea is generalized to stochastic feedforward nonlinear time-delay systems (1). The underlying philosophy of this approach is that the state-feedback controller is first constructed for system (7) without considering the drift and diffusion terms, and then a low gain κ in (6) (whose the value range is (28)) is introduced to state-feedback controller to dominate the drift and diffusion terms.
Remark 14. Due to the special upper-triangular structure and the appearance of time-varying delay, there is no efficient method to solve the stabilization problem of system (1). By combining the homogeneous domination approach with stochastic nonlinear time-delay system criterion, the state-feedback stabilization of system (1) was perfectly solved in this paper.
Remark 15. One of the main obstacles in the stability analysis is how to deal with the effect of time-varying delay. In this paper, by constructing an appropriate Lyapunov-Krasovskii functional (17), this problem was effectively solved.
Remark 16. It is worth pointing out that the rigorous proof of Theorem 12 is not an easy job.
5. A Simulation Example
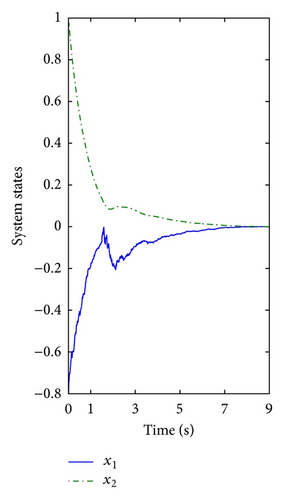
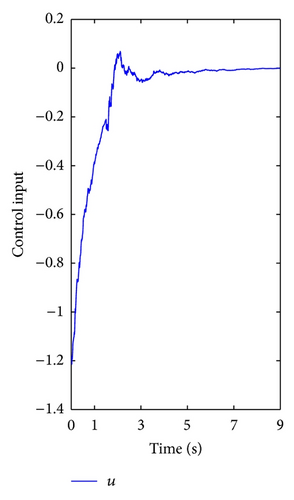
In simulation, we choose the initial values x1(0) = −0.8, x2(0) = 1, and κ = 0.3. Figure 1 demonstrates the effectiveness of the state-feedback controller.
6. A Concluding Remark
By using the homogeneous domination approach, this paper further studied the state-feedback stabilization problem for a class of stochastic feedforward nonlinear time-delay systems (1). The delay-independent state-feedback controller is explicitly constructed such that the closed-loop system is globally asymptotically stable in probability.
There still exist some problems to be investigated. One is to consider the output-feedback control of switched stochastic system (1) by using average dwell time method in [32]. Another is to find a practical example (similar to [33–35]) for system (1). The last is to generalize the networked control systems (such as [36–41]) to stochastic feedforward networked systems.
Conflict of Interests
The authors declare that there is no conflict of interests.
Acknowledgments
The authors would like to express sincere gratitude to editor and reviewers for their helpful suggestions in improving the quality of this paper. This work was partially supported by the National Natural Science Foundation of China (nos. 61304002, 61304003, 61203123, and 61304054), the Fundamental Research Funds for the Central Universities of China (no. 11CX04044A), the Shandong Provincial Natural Science Foundation of China (no. ZR2012FQ019), and the Polish-Norwegian Research Programme operated by the National Center for Research and 24 Development under the Norwegian Financial Mechanism 2009–2014 in the frame of Project Contract (no. Pol-Nor/200957/47/2013).
Appendix
Proof of Lemma 11. According to (3), (7), (10), and (11), one has
Using (10) and Lemma 7, one obtains
Choosing




