Advances in Materials Science and Engineering
Volume 2013, Issue 1 143208
Research Article
Open Access

Average Fracture Energy for Crack Propagation in Postfire Concrete

Kequan Yu, 

Kequan Yu

College of Civil Engineering, Tongji University, Shanghai 200092, China tongji.edu.cn

Search for more papers by this author
Jiangtao Yu, 

Corresponding Author

Jiangtao Yu

College of Civil Engineering, Tongji University, Shanghai 200092, China tongji.edu.cn

Search for more papers by this author
Zhoudao Lu, 

Zhoudao Lu

College of Civil Engineering, Tongji University, Shanghai 200092, China tongji.edu.cn

Search for more papers by this author
First published: 30 November 2013
https://doi.org/10.1155/2013/143208
Citations: 3
Academic Editor: Filippo Berto

Abstract

Wedge-splitting tests of postfire concrete specimens were carried out in the present research to obtain the load-displacement curves. Ten temperatures varying from room temperature to 600°C were employed. In order to calculate the accurate fracture energy, the tails of load-displacement curves were best fitted using exponential and power functions. Three fracture energy quantities (fracture energy GF, stable fracture energy GFS, and unstable fracture energy GFU) with their variation tendency and their mutual relationship were determined to predict energy consumption for the complete fracture propagation. Additionally, the stable fracture work WFS was also calculated. All these fracture parameters sustain an increase-decrease tendency which means that the fracture property of postfire concrete shares the same tendency.

1. Introduction

Since the application of fracture mechanics to concrete, the energy consumption for crack propagation in concrete has been a popular topic. For concrete, the specific fracture energy GF has been proven to be a useful parameter in the structure design and fracture behavior modeling. The specific fracture energy of concrete was defined based on a tensile test as the energy absorbed per unit crack area in widening the crack from zero to or beyond the critical value above which no stress can transmit [1]. Based on the work-of-fracture principle, three-point bending test [2], compact tension [3], and wedge-splitting method [4] were proposed as alternative methods to determine the specific fracture energy GF. It is computed as the area under the entire imposed load P and load-line displacement curve divided by the projected area of uncracked ligament, so the fracture energy GF represents the average or nominal energy consumption of concrete for an entire crack propagation process.

The existence of fracture process zone FPZ ahead of a crack is now well accepted. Since the 1970s, it has been known that the evolution of the FPZ undergoes two distinct periods—precritical stable crack growth and unstable fracture process [5]. There is no doubt that crack propagation is accompanied by energy dissipation, and the motive for crack propagation comes from either work provided by the imposed load or released strain energy. Fracture energy is one appropriate consideration to describe the amount of energy consumed during crack propagation process.

It is worth noting that the fracture energy can only represent the amount of average energy dissipation for entire crack propagation from crack initiation to complete failure without characterizing crack stable propagation and unstable fracture periods. So even with GF, it is still not clear how much energy is dissipated during those two crack extension periods. Xu et al. [6] proposed two new concepts the stable fracture energy GFS and unstable fracture energy GFU to describe fracture responses for different crack propagation periods. It is found that GFS kept constant for different ligament lengths, whereas GF and GFU showed the apparent size effect. But the accurate calculation of fracture surface remains unsolved. It is known that the true path of crack extension is tortuous, not straight as expected. The projected area underestimates the true fracture area. Hence, these parameters are actually nominal values.

The fracture energy of postfire concrete has been studied by several researchers [7–12]. It is found that the residual fracture energy sustained an increase-decrease tendency with the turning point at approximately 450°C. The increase tendency is due to the energy dissipation of microcracks distributing in the concrete, whereas the thermal damage induced by high temperatures reduces the residual fracture energy. However, in these researches, the influence of loading-displacement tail was unknown or not considered.

In present paper, wedge-splitting experiments of under ten temperatures levels varying from 20°C to 600°C and the specimens size of 230 mm × 200 mm × 200 mm with initial-notch depth ratios 0.4 are implemented [12]. Based on the work-of-fracture idea, the residual fracture energy GF is calculated considering the influence of load-displacement tail. Furthermore, the fracture energy consumption for crack stable extension and unstable extension, that is, GFS, GFU, is investigated. However, the true fracture surface remains undetermined and extremely difficult for specimens subjected to high temperatures, so these three fracture energy parameters are still nominal values. Hence, corresponding to GFS and GFU, the stable and unstable fracture work which neglect the fracture surface and their variation about temperatures are thus determined. From these parameters the fracture properties of postfire concrete could be described.

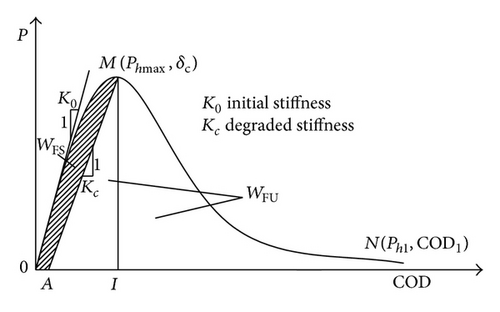
2. Fracture Energies for an Entire Crack Propagation Period

Based on the global energy balance principle, the work performed by a generalized force P on its displacement will be transformed into energy: one part of energy is stored in the body in the form of strain energy and the other part is used for crack propagation. It can be mathematically written as [6]:
()
where GFi = average energy needed for unit crack propagation during period from crack initiation to any instant of time i; Ai = newly formed fracture area for this period; the product of these two quantities represents the energy absorbed for crack propagation during this period; Wi = work performed by the external force P during the same period; Ui = increase of elastic strain energy of the body until time i; δi = crack opening displacement corresponding to P. If time i is approaching the failure terminal point i = 1, where the load drops to zero, then GFi in (1) will reduce to
()
where GF = RILEM fracture energy; W = total energy provided by the external force P for crack propagation; Alig = projected fracture area perpendicular to the tensile stress direction; b = specimen thickness; h = specimen height; a0 = initial crack length.
During the stable crack propagation period, the load will increase up to its peak value Pmax  with its corresponding displacement reaching CODc; see Figure 1. So, based on (1), the average energy absorbed during this period can be evaluated by
()
where GFS by naming the stable fracture energy = average energy needed for the crack to grow unit area during the crack stable propagation; AS = change in fracture area; WFS = WOAMO = energy provided for stable crack propagation as shown in Figure 1 by the shaded area; WP = WOIMO = work performed by the external force P for crack increases its area AS; ΔUS = WAIMA = increased elastic strain energy of the body; and CODc = critical crack opening displacement.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Energy consumption for an entire crack propagation period.
From the definition of the stable fracture energy GFS, it is implied that the work from the imposed load P is expended in two forms during the crack stable propagation: one part is stored in the body in the form of the elastic strain energy (ΔUS) and the other part is the energy absorbed by the fracture zone mainly to counteract the resistance caused by the cohesive forces along the FPZ. In the same way, the unstable fracture energy, denoted by GFU, is defined based on energy equilibrium as
()
where WU = energy needed for the crack unstable propagation period and AU = change in fracture area. During this period, the stored energy is completely released until the deformation reaches its maximum value COD1 when the load closes to zero. Similar to the RILEM fracture energy GF, the establishment of the stable fracture energy GFS and unstable fracture energy GFU rests upon the implicit assumption that no other energy consumption occurs outside the fracture zone.

3. Experimental Program and Experimental Phenomena

In this test, concrete specimens were prepared using an ordinary silicate cement PO. 42.5 produced conforming to the Chinese standard. Coarse aggregate was calcareous crushed stone with a maximum size of 16 mm, and river sand was used as the fine aggregates and its maximum diameter was 5 mm. Details of the mix proportioning (by weight) used for concrete and some mechanical properties are Cement : Sand : Limestone Coarse aggregate : Water : fly ash = 1.00 : 3.44 : 4.39 : 0.80 : 0.26.

Fracture properties of concrete were determined by means of the wedge splitting test [4]. The test setup and geometry of the specimen are schematically represented in Figure 2. Compared to three-point bending notched beams, the wedge-splitting test has following advantages. For the three-point bending beams, inaccurate measurement of load-point displacement and the self-weight of the specimen could influence the real value of the fracture energy. During the test, beams should be carefully handled due to their heavy weight. However, using the WS specimens, the recorded COD in a horizontal plane is not affected by the crushing of the specimen at the supports or some other factors. Besides, the WS specimens are simple and easily prepared in laboratories or on site.

Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Test setup and geometry of specimens.

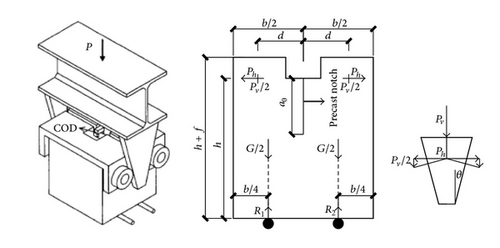
A total of 50 concrete specimens with the same dimensions 230 × 200 × 200 mm were prepared; the geometry of the specimens and the test setup are shown in Figure 2 (b = 200 mm, d = 65 mm, h = 200 mm, f = 30 mm, a0 = 80 mm, and θ = 15°). All the specimens had a precast notch of 80 mm height and 3 mm thickness, achieved by placing a piece of steel plate into the molds prior to casting. Each wedge splitting specimen was embedded with a thermal couple in the center of specimen for temperature control.

Nine heating temperatures, ranging from 65°C to 600°C (Tm = 65°C, 120°C, 200°C, 300°C, 350°C, 400°C, 450°C, 500°C, and 600°C), were adopted with the ambient temperature as a reference. Because it was recognized that the fracture behavior measurements were generally associated with significant scatter, five repetitions were performed for each temperature.

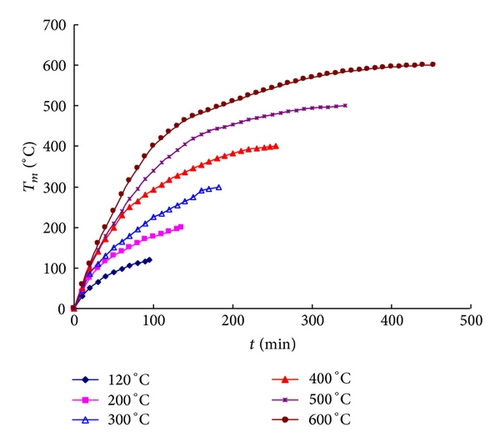
An electric furnace with net dimensions 300 × 300 × 900 mm was used for heating. When the designated Tm was reached, the furnace was shut down, and the specimens were naturally cooled for 7 days prior to the test. It averagely took 50, 95, 135, 182, 218, 254, 294, 342, and 453 minutes for the specimens to reach the final temperatures, respectively (from 65°C to 600°C). Figure 3 shows the typical temperature history for several cases with different maximum temperatures. After heating, microcracks disperse on the specimen surface, especially for temperatures higher than 200°C (see in Figure 4).

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Typical temperature history of specimens.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Microcracks on specimen surface (600°C).

The fracture surfaces at different temperature intervals (20°C, 200°C, 350°C, 450°C, and 600°C) are shown in Figure 5, which became lighter but more tortuous with increasing temperatures.

Details are in the caption following the image
Figure 5 (a) Fracture surface of 20°C
Open in figure viewerPowerPoint
Fracture surfaces of postfire specimens.
Details are in the caption following the image
Figure 5 (b) Fracture surface of 600°C
Open in figure viewerPowerPoint
Fracture surfaces of postfire specimens.
Details are in the caption following the image
Figure 5 (c) Fracture surfaces at typical temperatures (20°C, 200°C, 350°C, 450°C, and 600°C)
Open in figure viewerPowerPoint
Fracture surfaces of postfire specimens.
A universal machine with a maximum capacity of 1000 kN was used to conduct the wedge splitting tests. During the test, the vertically applied load Pv and the crack opening displacement COD along the horizontal load line were simultaneously recorded through a data acquisition system. Referring to Figure 2, the splitting force Ph is actually the horizontal component of the force acting on the bearing. Taking the wedge angle into consideration, its relation with the recorded applied load Pv can be developed based on force equilibrium ignoring the small influence from the friction for different roller bearings:
()

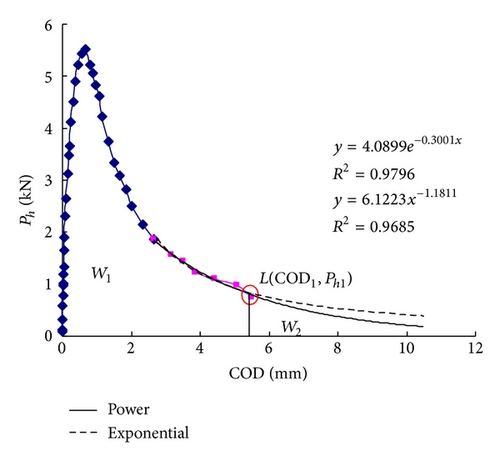
To obtain the complete P-  COD curves (shown in Figure 6), the test rate was fixed at 0.4 mm/min, such that it took approximately 20 minutes to complete a single test of specimens subjected to less than 300°C and 30 minutes for beyond 300°C.

Details are in the caption following the image
Figure 6 (a) Ph versus COD curves of specimens at 120°C
Open in figure viewerPowerPoint
P  versus CMOD curves of specimens with temperatures.
Details are in the caption following the image
Figure 6 (b) Ph versus COD curves of specimens at 450°C
Open in figure viewerPowerPoint
P  versus CMOD curves of specimens with temperatures.
Details are in the caption following the image
Figure 6 (c) Ph versus COD curves of specimens at 600°C
Open in figure viewerPowerPoint
P  versus CMOD curves of specimens with temperatures.
Details are in the caption following the image
Figure 6 (d) Typical Pv versus COD curves of specimens at all temperatures
Open in figure viewerPowerPoint
P  versus CMOD curves of specimens with temperatures.

The fracture of specimen is essentially due to the bending moment caused by the horizontal splitting force Ph, vertical component 1/2Pv, and self-weight of the specimen. Two symmetrical supports are placed below the center of gravity of each half of the specimen. In doing so, the influence of the dead weight of the specimen and part of the vertical component force on the calculation of the fracture energies could be counteracted. Each roll axis is fixed at the same horizon as the lower plane of the groove and is very close to the center of gravity of each half of the specimen in the vertical position (shown in Figure 2). Due to the carefulness in the choice of the specimen geometry, the roll axis location, and the placement of the supports, the horizontal force Ph contributes most to fracturing the specimen. Therefore, Ph-COD curves were directly used in the calculation of the RILEM fracture energy GF, stable fracture energy GFS, and unstable fracture energy GFU.

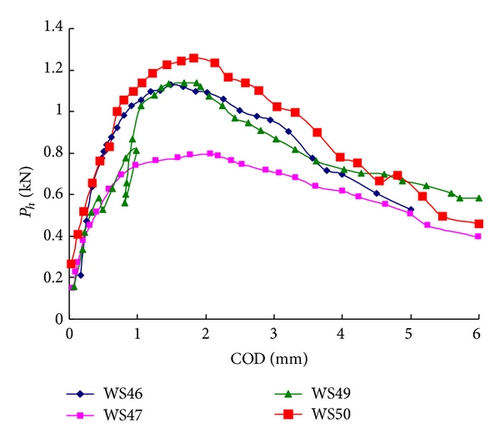
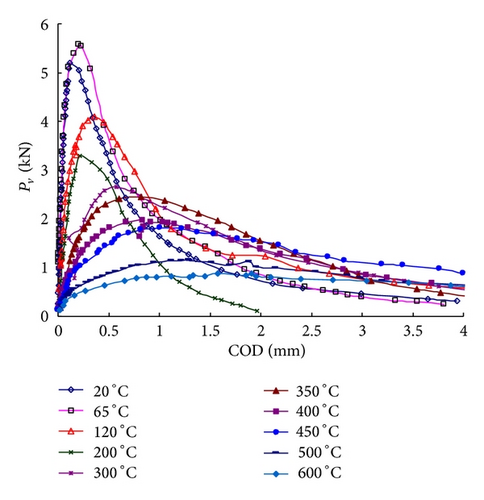
For our test results, the Ph-COD curves could be easily obtained from the monitored Pv-COD curves and (5). Figure 6 contains the plots of Ph-COD curves for several temperatures and typical Pv-COD curves for all temperatures.

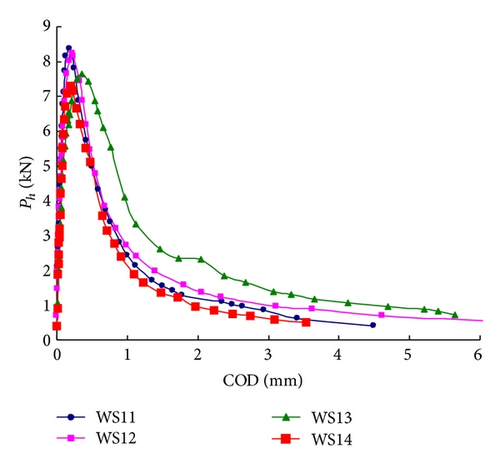
From Figure 6(a) to 6(c), it is found that with the increasing of temperature (20°C–600°C), the divergence between the curves for the same temperature is more significant. In particular 600°C, the ultimate load Pu of specimen WS50 is one time higher than the one of specimen WS47. Additionally, the whole loading process is not stable for specimens WS49 (a sudden snap-back) due to the thermal damage induced by high temperature. Figure 6(d) shows the typical P-COD curves of all temperatures. The ultimate load Pu decreases significantly with increasing temperatures Tm, whereas the crack mouth opening displacement (COD) increases with Tm. The initial slope of ascending branches decreases with heating temperatures, and the curves become gradually shorter and more extended.

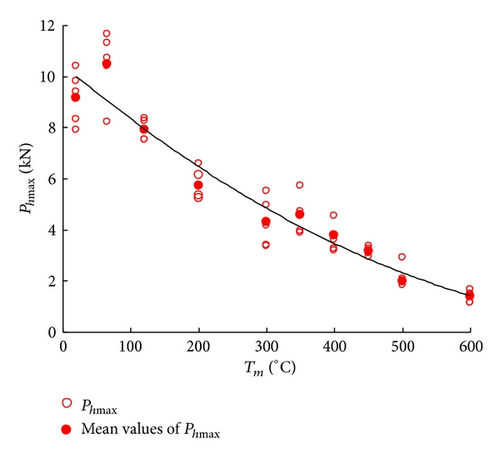
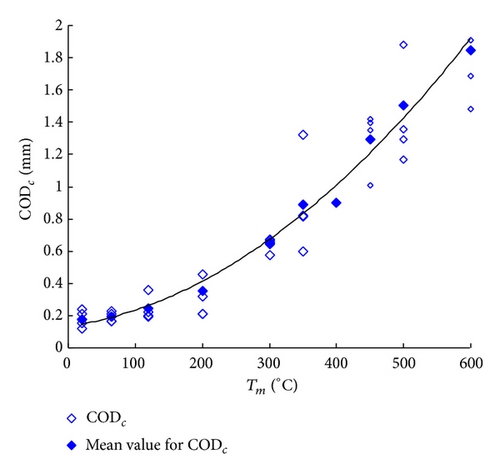
It is found that the ultimate load Phmax  decreases with the increasing temperatures, whereas the CODc increases with Tm (Figure 8). The average value of Pu decreases from 9.17 kN at ambient temperature to 7.92 kN at 120°C, 4.29 kN at 300°C, 3.16 kN at 450°C, and finally 1.38 kN at 600°C, with a final drop of 85%. The value of CODc increases from 0.178 mm at ambient temperature to 0.352 mm at 200°C, 0.901 mm at 400°C, and 1.848 mm at 600°C, nearly 10 times as the ambient value.

4. Experimental Results and Analysis

4.1. Determination of Residual Fracture Energy GF

In the calculation of RILEM fracture energy GF, two things should be carefully considered. One thing is that the work done by the self-weight of loading device should be taken into account. In present experiments, the loading device is attached to the testing machine and the Ph-COD curve includes the self-weight; hence the work should not be calculated again. The other concern pertains to the tail part of the Ph-COD curve: the recorded point (Ph1, COD1) is just one point when the experiment stops, not the actual point of when the load drops to zero. Therefore, cutting the load-deflection tail may lead to noticeable inaccuracy in the true value of fracture energy. Thus, to account for these two factors, the actual RILEM fracture energy GF based on the work-of-fracture method becomes (see Figure 9)
()
where W1 = measured work enclosed by the Ph-COD curve until COD = COD1; Alig = fresh fracture area; W2 is the work caused by tail effect part. For W2, curve fitting technology based on Excel software was used to get its approximate value. In previous research from the test results at ambient temperature [13], it was found out that the descending branch of the Ph-COD curve after one-third of the peak load could be well described by power function (the coefficient of determination R2 for each curve is close to 1). This study indicates that for specimens subject to no more than 120°C, the power function is more accurate; however, for specimens subject to higher temperatures, exponential function is more suitable (see Figure 9).
For power function Ph = β  ×  COD−λβ, λ > 0, where β, λ = constants for fitting curves. And then the unrecorded work W owning to cutting load-deflection tail can be written as
()
For exponential function Ph = m × e−n×CODm, n > 0, where m, n = constants for fitting curves. And then the unrecorded work W owning to cutting load-deflection tail can be written as
()

The parameters of β, λ for 20°C~120°C and m, n for 200°C~600°C, and the value of w1, w2 is listed in Table 1.

Table 1. Parameters calculated from wedge-splitting test.
Specimen Temperature Phmax (kN) E (GPa) ac (mm) β/m λ/n R2 W1 W2 CODc (mm) COD1 (mm) K0 (kN/mm) Kc (kN/mm)
WS1 20°C 8.304 15.30 0.107 1.484 2.273 0.970 5.231 0.389 0.174 1.926 87.081 79.219
WS2 9.407 20.51 0.097 3.131 1.206 0.998 10.468 1.140 0.205 4.914 116.710 113.648
WS3 10.379 20.66 0.114 2.464 1.117 0.991 8.699 1.818 0.195 3.280 117.610 110.633
WS4 7.884 18.88 0.112 1.599 3.224 0.964 5.128 0.137 0.152 1.903 107.480 98.911
WS5 9.364 15.45 0.107 2.048 1.683 0.991 6.970 0.735 0.199 2.657 87.940 80.103
  
Average   9.068 18.16 0.107 — — 0.983 7.299 0.844 0.185 2.936 103.364 96.503
  
WS6 65°C 11.282 21.73 0.113 2.781 1.506 0.996 9.238 0.984 0.195 3.205 123.690 116.172
WS7 8.151 24.79 0.132 2.739 0.987 0.999 10.320 1.263 0.215 6.072 141.100 136.109
WS8 10.379 19.43 0.115 6.114 1.992 0.954 11.004 0.702 0.212 4.549 110.560 105.418
WS9 10.681 23.25 0.119 2.658 1.030 0.993 9.283 2.250 0.164 3.535 132.330 124.685
WS10 11.610 16.60 0.107 3.185 1.252 0.983 11.466 1.071 0.190 5.324 94.490 90.418
  
Average   10.421 21.16 0.117 — — 0.985 10.262 1.254 0.195 4.537 120.434 114.560
  
WS11 120°C 8.353 10.65 0.095 2.477 1.085 0.990 8.423 1.094 0.191 3.418 60.638 57.254
WS12 8.226 11.87 0.107 2.667 0.890 0.999 10.624 1.803 0.224 6.443 67.564 65.212
WS13 7.631 9.48 0.119 4.340 0.998 0.980 13.227 2.487 0.357 5.641 53.926 50.511
WS14 7.302 15.42 0.117 2.139 1.153 0.998 6.934 1.357 0.198 3.534 87.758 82.839
WS15 — — — — — — — — — — — —
  
Average   7.878 11.85 0.109 — — 0.992 9.802 1.685 0.243 4.759 67.472 63.954
  
WS16 200°C — — — — — — — — — — — —
WS17 6.466 11.58 0.127 2.266 1.526 0.952 6.260 0.520 0.284 2.558 65.913 57.759
WS18 5.884 6.98 0.115 2.268 2.982 0.995 5.035 0.129 0.335 1.968 39.732 32.967
WS19 5.071 9.17 0.127 2.770 2.087 0.969 5.397 0.265 0.306 2.786 52.178 46.456
WS20 5.228 7.00 0.130 2.530 0.366 0.903 7.605 1.250 0.458 4.447 39.866 35.765
  
Average   5.662 8.68 0.125 — — 0.955 6.074 0.541 0.346 2.940 49.422 43.237
  
WS21 300°C 3.341 2.45 0.121 4.023 0.361 0.981 10.019 0.491 0.792 3.101 13.939 11.004
WS22 5.513 3.49 0.117 4.090 0.300 0.987 13.570 1.105 0.667 5.065 19.869 17.251
WS23 3.371 1.91 0.113 6.985 0.610 0.982 7.727 0.475 0.672 4.957 10.854 9.384
WS24 4.761 1.99 0.105 4.285 0.345 0.990 12.552 0.987 0.728 6.816 11.350 10.138
WS25 4.076 4.03 0.137 2.172 0.206 0.963 11.532 1.667 0.869 6.874 22.960 20.438
  
Average   4.213 2.78 0.119 — — 0.981 11.080 0.945 0.746 5.363 15.794 13.643
  
WS26 350°C 5.701 6.05 0.131 5.702 0.447 0.995 12.290 1.475 0.599 4.549 34.409 29.878
WS27 3.840 2.03 0.125 6.245 0.335 0.958 14.150 1.490 1.003 6.768 11.538 9.829
WS28 4.718 3.60 0.131 5.553 0.454 0.997 11.312 1.107 0.815 4.053 13.490 16.360
WS29 4.554 3.38 0.130 9.025 0.608 0.995 11.635 0.355 0.821 5.940 19.240 16.582
WS30 3.931 3.21 0.134 7.135 0.532 0.990 10.251 0.654 0.832 5.335 18.279 15.427
  
Average   4.549 3.65 0.130 — — 0.987 11.927 1.016 0.814 5.329 19.391 17.615
  
WS31 400°C 3.584 2.56 0.136 3.934 0.307 0.999 11.737 1.033 0.921 6.937 14.557 12.391
WS32 3.039 1.42 0.126 21.138 0.828 0.992 9.300 0.226 0.904 5.614 8.084 6.331
WS33 3.228 2.12 0.114 2.100 0.224 0.995 8.533 1.575 0.842 5.819 7.348 6.419
WS34 4.476 1.71 0.111 4.208 0.322 0.929 13.388 0.986 0.985 5.940 12.035 8.463
WS35 — — — — — — — — — — — —
  
Average   3.582 1.95 0.122 — — 0.979 10.740 0.955 0.913 6.078 10.506 8.401
  
WS36 450°C 3.336 1.41 0.125 5.280 0.299 0.977 13.124 1.553 1.224 5.625 8.037 6.289
WS37 — — — — — — — — — — — —
WS38 3.118 1.46 0.123 10.235 0.543 0.981 10.601 0.978 1.057 5.672 8.291 6.216
WS39 3.056 1.34 0.127 2.518 0.137 0.995 11.955 3.960 1.281 6.784 7.611 6.099
WS40 2.935 1.58 0.137 4.328 0.226 0.998 13.896 2.395 1.394 6.000 8.988 6.900
  
Average   3.111 1.45 0.128 — — 0.988 12.394 1.663 1.239 6.020 8.232 6.376
  
WS41 500°C — — — — — — — — — — — —
WS42 2.153 1.76 0.146 3.056 0.245 0.976 7.762 3.054 1.284 5.153 7.251 7.506
WS43 2.857 1.09 0.119 3.648 0.306 0.979 10.092 1.342 1.174 6.533 6.179 5.069
WS44 1.929 0.75 0.109 2.234 0.153 0.968 8.758 4.119 1.225 6.591 4.243 3.651
WS45 1.838 1.48 0.147 2.300 0.186 0.996 7.826 3.012 1.354 6.225 6.078 6.591
  
Average   2.194 1.27 0.130 — — 0.977 8.002 2.494 1.259 6.125 5.938 5.704
  
WS46 600°C 1.129 0.47 0.130 2.102 0.278 0.931 4.197 1.280 1.482 7.000 2.656 2.094
WS47 1.474 0.48 0.128 3.018 0.238 0.954 7.245 2.236 1.784 10.000 2.718 2.233
WS48 1.649 1.14 0.152 1.992 0.132 0.979 8.390 4.551 1.908 7.100 3.909 2.858
WS49 1.138 0.38 0.131 1.183 0.120 0.971 5.018 2.950 1.865 10.000 1.165 1.761
WS50 1.243 0.38 0.124 2.507 0.285 0.943 5.273 1.280 1.644 8.000 1.174 1.727
  
Average   1.326 0.57 0.133 — — 0.956 6.025 2.460 1.737 8.420 2.324 2.135

Some necessary test results are tabulated in Table 1, including the maximum value of the horizontal load Phmax  and its corresponding crack opening displacement CODc, the endpoint where Ph1 approaches zero and the crack opening displacement arrives at COD1, the initial slope of Ph-COD, that is, the initial stiffness K0, and the modulus of elasticity E.

Hence, the residual fracture energy described by (1) could be calculated. The values are listed in Table 2 and are shown in Figure 10.

Table 2. Fracture energies for crack propagation.
Specimen Temperature W0 (Nm) Alig (m2) GF (Nm−1) WOIMA (Nm) WAIMA (Nm) WFS (Nm) AFS (m2) GFS (Nm−1) WFU (Nm) AFU (m2) GFU (Nm−1)
WS1 20°C 5.620 0.024 234.147 1.217 0.407 0.810 0.005 152.502 4.809 0.019 257.361
WS2 11.608 483.664 1.575 0.388 1.187 0.003 350.795 10.421 0.021 504.972
WS3 10.517 438.217 2.124 0.470 1.654 0.007 242.557 8.863 0.017 515.877
WS4 5.265 219.394 0.994 0.314 0.680 0.006 107.537 4.586 0.018 259.384
WS5 7.705 321.055 1.693 0.525 1.169 0.005 212.824 6.536 0.019 353.175
  
Average   8.143   339.295 1.521 0.421 1.100 0.005 213.243 7.043 0.019 378.154
  
WS6 65°C 7.666 0.024 425.907 1.791 0.535 1.255 0.007 281.835 6.411 0.017 480.239
WS7 8.687 482.619 1.076 0.241 0.835 0.010 113.926 7.852 0.014 768.132
WS8 8.779 487.745 1.475 0.509 0.966 0.007 208.612 7.813 0.017 602.385
WS9 8.649 480.507 1.027 0.440 0.587 0.008 118.113 8.062 0.016 656.640
WS10 9.402 522.360 1.419 0.733 0.686 0.005 210.596 8.716 0.019 614.693
  
Average   8.637   479.828 1.357 0.492 0.866 0.007 186.616 7.771 0.017 624.418
  
WS11 120°C 7.137 0.024 396.516 1.335 0.588 0.746 0.003 251.423 6.391 0.021 416.985
WS12 9.321 517.822 1.475 0.511 0.964 0.005 178.684 8.357 0.019 616.201
WS13 11.785 654.732 2.079 0.560 1.520 0.008 193.937 10.266 0.016 878.097
WS14 6.218 345.463 1.044 0.312 0.732 0.007 98.944 5.486 0.017 455.357
WS15 — — — — — — — — — —
  
Average   8.615   478.633 1.483 0.493 0.991 0.006 180.747 7.625 0.018 591.660
  
WS16 200°C — 0.024 — — — — — — — — —
WS17 6.780 282.509 1.522 0.345 1.176 0.009 123.021 5.604 0.015 385.812
WS18 5.163 215.135 1.556 0.525 1.031 0.007 146.955 4.132 0.017 243.300
WS19 5.662 235.913 1.252 0.270 0.982 0.009 104.764 4.680 0.015 320.014
WS20 8.854 368.937 1.828 0.365 1.463 0.010 145.364 7.391 0.014 530.467
  
Average   6.615   275.624 1.540 0.376 1.163 0.009 130.026 5.452 0.015 369.898
  
WS21 300°C 10.510 0.024 437.920 2.005 0.439 1.566 0.008 188.640 8.944 0.016 568.895
WS22 14.675 611.467 3.546 0.820 2.726 0.007 364.621 11.949 0.017 723.160
WS23 8.202 341.770 2.048 0.579 1.469 0.007 220.394 6.733 0.017 388.453
WS24 13.539 564.120 3.065 1.081 1.984 0.005 404.514 11.555 0.019 605.107
WS25 13.200 549.990 2.552 0.389 2.163 0.011 190.295 11.037 0.013 870.055
  
Average   12.025   501.053 2.643 0.662 1.982 0.008 273.693 10.044 0.016 631.134
  
WS26 350°C 13.765 0.024 573.540 2.689 0.511 2.179 0.010 211.652 11.586 0.014 845.346
WS27 15.639 651.638 2.589 0.703 1.887 0.009 207.566 13.753 0.015 922.314
WS28 12.420 517.489 3.827 0.919 2.908 0.010 317.145 9.512 0.014 664.527
WS29 11.990 499.602 2.900 0.611 2.289 0.010 228.349 9.701 0.014 694.230
WS30 10.905 454.375 2.796 0.475 2.320 0.011 216.312 8.585 0.013 646.739
  
Average   12.944   539.329 2.960 0.644 2.317 0.010 236.205 10.627 0.014 754.631
  
WS31 400°C 12.770 0.024 532.090 2.240 0.484 1.756 0.011 156.074 11.014 0.013 860.665
WS32 9.526 396.932 2.678 0.656 2.022 0.009 207.133 7.504 0.015 516.314
WS33 10.109 421.188 2.411 0.760 1.651 0.007 242.302 8.457 0.017 491.692
WS34 14.374 598.926 3.638 0.918 2.720 0.006 401.879 11.654 0.018 668.062
WS35 — — — — — — — — — —
  
Average   11.695   487.284 2.742 0.705 2.037 0.008 251.847 9.658 0.016 634.184
  
WS36 450°C 14.677 0.024 611.530 3.255 0.779 2.477 0.009 277.088 12.200 0.015 809.983
WS37 — — — — — — — — — —
WS38 11.579 482.451 3.284 0.669 2.615 0.009 303.750 8.964 0.015 582.382
WS39 15.914 663.097 3.281 0.704 2.578 0.009 272.015 13.337 0.015 918.284
WS40 16.291 678.790 3.847 0.532 3.315 0.011 292.743 12.976 0.013 1023.630
  
Average   14.057   608.967 3.417 0.671 2.746 0.010 286.399 11.869 0.014 833.570
  
WS41 500°C — 0.024 — — — — — — — — —
WS42 10.816 450.668 2.080 0.355 1.725 0.013 138.244 9.091 0.011 831.501
WS43 11.434 476.413 2.890 0.743 2.146 0.008 272.496 9.288 0.016 576.031
WS44 12.877 536.544 1.495 0.475 1.021 0.006 170.514 11.856 0.018 652.188
WS45 10.838 451.571 2.720 0.308 2.412 0.013 186.562 8.426 0.011 785.892
  
Average   10.496   478.799 2.296 0.470 1.826 0.010 191.954 9.665 0.014 711.403
  
WS46 600°C 5.477 0.024 228.226 1.404 0.287 1.117 0.010 110.974 4.361 0.014 312.890
WS47 9.481 395.057 2.526 0.460 2.066 0.010 213.423 7.415 0.014 517.849
WS48 12.941 539.225 2.621 0.389 2.232 0.014 155.808 10.709 0.010 1107.140
WS49 7.968 331.988 1.514 0.635 0.879 0.010 115.238 7.088 0.014 491.494
WS50 6.554 273.074 1.749 0.773 0.976 0.009 151.878 5.578 0.015 342.831
  
Average   8.484   353.514 1.963 0.509 1.454 0.011 149.464 7.030 0.013 632.922

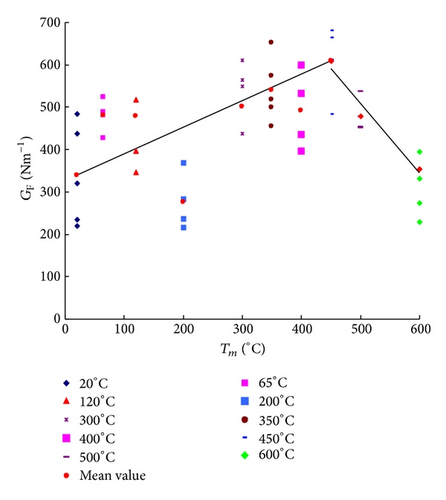
Though the residual fracture energy at each temperature has significant scatter, Figure 10 shows that the average values sustain an increase-decrease tendency with Tm. From 20°C to 450°C, average GF increases from 339.3 Nm−1 to 609 Nm−1, while the temperature reaches 600°C and the fracture energy falls back to 307.8 Nm−1. The detailed explanation would be seen elsewhere [12].

4.2. Determination of Stable Fracture Energy GFS and Unstable Fracture Energy GFU

As an extension of fracture energy GF, two other energy-based fracture characteristics, the stable fracture energy GFS and unstable fracture energy GFU, are proposed to describe fracture responses for different crack propagation periods. The analysis shows that fracture energy GF is actually the weighed average of GFS and GFU, and GFS and GFU could be regarded as two components of GF. This is very helpful in understanding the whole crack propagation process from the aspect of energy consumption.

To obtain the values of GFS and GFU, the critical effective crack length ac should first be determined for the calculation of the fracture areas AS and AU. Herein, the value ac was computed based on the double-K fracture model [14]:
()
where c = COD/P is the compliance of specimens, E is modulus of elasticity, b is specimen thickness, h is specimen height, and h0 is the thickness of the clip gauge holder. For calculation of critical value of equivalent elastic crack length ac, the value of crack mouth opening displacement (COD) and P are taken as CODc and Phmax , respectively. Equation (9) is valid for 0.2–0.8 within 2% accuracy. The value of ac is reported in Table 1.
In a typical load-displacement curve shown in Figure 1, K0 is the initial stiffness of the load-displacement curve before the start of the fracture process. At critical state when the load arrives at its peak value Pmax  and its corresponding displacement reaches CODc, the stiffness Kc may not be the same as the initial K0. The degradation of stiffness is the result of crack propagation. To make it simple, here, the value of K at any value of displacement is assumed to be linear with increased deformation [15].
()
where COD 1 = final deformation when the load P approaches zero and COD 0 = displacement before which the stiffness is still kept at K0. At the origin of P-COD curve, the initial tangent stiffness is K0. The stiffness becomes degraded beyond the origin point; hence COD 0 is presumed to be zero. It is clear from (10) that K = K0 when COD = 0 and K = 0 when = COD 1, and K is assumed to be a linear function with respect to the displacement. With the crack opening displacement COD = CODc, the stiffness Kc at this point could approximately be obtained through (10). Note that P-COD is a general term for load-displacement; in our case, the load is the horizontal force Ph and its corresponding displacement is the COD. Therefore, with K0, COD 1, and CODc, the approximate degraded stiffness Kc can be gained from (10) and the result is shown in Table 1. Figure 11 shows that the values of stiffness Kc decrease monotonously with temperature due to the thermal damage induced by high temperatures.
The stable fracture energy GFS and unstable fracture energy GFU can be derived by following (11)~(13). The specific values of GFS and GFU are compiled in Table 2:
()
()
()

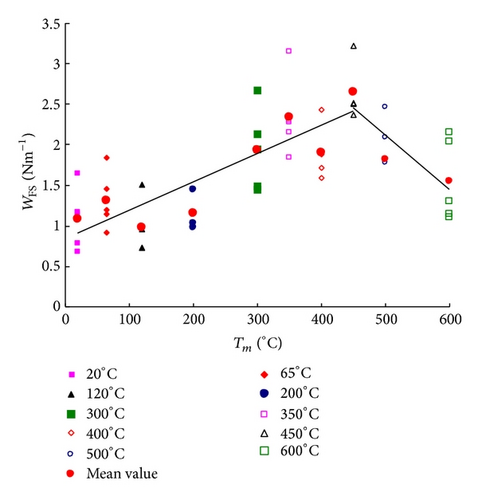
Figure 12 shows the variation of stable fracture energy GFS with temperatures. Similar to the residual fracture energy GF, it also keeps an increase-decrease tendency with temperatures. Temperatures less than 120°C appear not to induce much thermal damage to concrete, so the cracking resistance almost keeps constant. The values of stable fracture energy GFS at these temperatures are 213 Nm−1, 186 Nm−1, and 180 Nm−1, respectively. The fracture surfaces tend to be more tortuous between 200°C and 450°C than those observed at lower temperatures (see Figure 4) and there exist several cracks competing to form the final fracture, so more energy was dissipated in these specimens. Additionally, the opening of microcracks on the surface and inside the specimens also dissipates energy (see Figure 3). Finally, higher heating temperatures would cause more micro cracks, dehydration, and decomposition and would degrade the resistance. After 450°C, cracking resistance continuously decreases with Tm.

Table 2 shows that the unstable fracture GFU also sustains an increase-decrease tendency with Tm, and its value is much larger than stable fracture energy. Two reasons for larger values of GFU are provided [5]. First, energy consumption besides the main fracture zone takes places for the whole fracture process. During the unstable fracture process, the energy consumption for plasticity or other nonlinear deformation beyond the main FPZ would be much higher, especially for specimens subjected to high temperatures. The other possible reason lies in the calculation of true fracture area. It is known that the interface (transition zone) between cement and aggregate is the weak link in microstructure for normal concrete, and crack propagation would proceed in the path where the energy needs are least. So the true path of crack extension is tortuous and the higher the temperature is, the more tortuous the fracture surface is (see Figure 4), not straight as expected. The projected area is used in the calculation of fracturing surface AS or AU, which underestimates the true fracture area. Since the crack experiences much longer distance for the unstable extension, which leads to a greater underestimation of the calculation of the newly fractured area AU, the calculated GFU is overestimated.

Moreover, in view of (11) and (12), another expression for the fracture energy GF with respect to GFS and GFU can be followed:
()
Since AS + AU = A, the fracture energy GF is the weighed average of GFS and GFU. However, for engineering application, the stable crack propagation is considered to be more important, because when the load exceeds the maximum value the whole structure would be in an unstable situation. Hence from Figures 7 and 9, it is concluded that the fracture property of postfire concrete sustains an increase-decrease tendency to 600°C, with a turning point at 450°C.
Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Variation tendency of Phmax with Tm.
Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Variation tendency of CODc with Tm.
Details are in the caption following the image
Figure 9 (a) Curve fitting for specimen of ambient temperature
Open in figure viewerPowerPoint
P-CMOD tail curve fitting of specimens.
Details are in the caption following the image
Figure 9 (b) Curve fitting for specimen of 200°C
Open in figure viewerPowerPoint
P-CMOD tail curve fitting of specimens.
Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
Residual fracture energy with Tm.
Details are in the caption following the image
Figure 11
Open in figure viewerPowerPoint
Stiffness Kc with Tm.
Details are in the caption following the image
Figure 12
Open in figure viewerPowerPoint
Stable fracture energy with Tm.

Furthermore, as mentioned above, the fracture surfaces of A, AS, AU are project areas, so GF, GFS, GFU are nominal fracture energies. To avoid the violence of fracture surface, the variation tendency of stable fracture work WFS is determined (see Figure 10). Similarly, WFS also keeps an increase-decrease tendency at the same turning temperature of 450°C.

5. Conclusions

Energy consumption during an entire crack propagation period has been investigated, including the fracture energy GF, stable fracture energy GFS, unstable fracture energy GFU, and stable fracture work WFS. The conclusions are as follows.
  • (1)

    Wedge-splitting tests of ten temperatures levels varying from room temperature to 600°C and the specimen size of 230 mm × 200 mm × 200 mm with initial-notch depth ratios 0.4 have been presented. Complete P-COD curves and the curve tails are obtained using exponential and power functions. For specimens subject to no more than 120°C, the power function is more accurate; for higher temperatures, exponential function is more suitable.

  • (2)

    Three fracture energy quantities corresponding to different aspects of fracture are proposed. The fracture energy GF in a general case only represents the average energy dissipation for an entire crack propagation process. GFS, the stable fracture energy, denotes the average energy absorption during crack stable propagation, and GFU is used to characterize the average energy consumption for crack unstable propagation and a higher value of GFU than GFS is observed. GF is actually the weighed average of GFS and GFU.

  • (3)

    However, for engineering applications, the stable crack propagation is considered to be more important. From the wedge-splitting tests of different temperatures, it is concluded that GF, GFS sustain an increase-decrease tendency to 600°C, with a turning point at 450°C. Furthermore, the variation of stable fracture work WFS is determined and shares the same tendency with GF and GFS (Figure 13). All these three parameters mean that the fracture property of postfire concrete sustains an increase-decrease tendency.

Details are in the caption following the image
Figure 13
Open in figure viewerPowerPoint
Stable fracture work with Tm.

Acknowledgments

The State Key Laboratory of Disaster Reduction in Civil Engineering (SLDRCE09-D-02) and Young Scientist Project of Natural Science Foundation of China (NSFC) have supported this research.

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.