Analysis of Stochastic Delay Predator-Prey System with Impulsive Toxicant Input in Polluted Environments
Abstract
A stochastic delay predator-prey model in a polluted environment with impulsive toxicant input is proposed and studied. The thresholds between stability in time average and extinction of each population are obtained. Some recent results are extended and improved greatly. Several simulation figures are introduced to support the conclusions.
1. Introduction
Environmental pollution by industries, agriculture, and other human activities is one of the most important socio-ecological problems in the world today. Due to toxins in the environment, lots of species have gone extinct, and many are on the verge of extinction. Thus, controlling the environmental pollution and the conservation of biodiversity are the major focus areas of all the countries around the world. This motivates scholars to study the effects of toxins on populations and to find out a theoretical persistence-extinction threshold.
Yang et al. [15] showed that in the following Lemma holds.
Lemma 1. For system (1), define
- (a)
If r10 < r11K1/γ, then lim t→+∞xi(t) = 0, i = 1,2.
- (b)
If r10 > r11K1/γ and , then and x2(t) goes to extinction.
- (c)
If , then , i = 1,2.
-
(Q1) In the real world, the growth of species depends on various environmental factors, such as temperature, humidity and parasites and so forth. Therefore population models should be stochastic rather than deterministic (May [25]). Thus, what happens if model (1) is subject to stochastic noises?
-
(Q2) In addition, time delays occur in almost every situation. Kuang [26] has pointed out that ignoring time delays means ignoring reality. Therefore, what happens if model (1) takes time delays into account?
-
(Q3) Can we improve the results given in Lemma 1?
Theorem 2. For system (3), define
- (i)
If θ1 < r11K1/γ, then both x1 and x2 go to extinction almost surely (a.s.); that is, lim t→+∞ xi(t) = 0 a.s., i = 1,2.
- (ii)
If θ1 > r11K1/γ and , then x2(t) goes to extinction and x1 is stable in time average a.s.; that is,
() - (iii)
If , then both x1 and x2 are stable in time average a.s.
()
Remark 3. By comparing Lemma 1 with our Theorem 2, we can see that on the one hand, if α1 = α2 = 0 and τ1 = τ2 = 0, then θi = ri0, , i = 1,2, and our stochastic delay system (3) becomes model (1); on the other hand, our results in Theorem 2 improve that in Lemma 1. Lemma 1 shows that the superior limit is positive, while Theorem 2 reveals that the limit exists and gives the explicit form of the limit. The contribution of this paper is therefore clear.
2. Proof
Lemma 4. For any given initial value , there is a unique global positive solution x(t) = (x1(t), x2(t)) T to the first two equations of system (3) a.s.
Proof. The proof is similar to Hung [29] by defining
Lemma 5 (see [13], [15].)System (10) has a unique positive γ-periodic solution , and for each solution (C10(t), C20(t), Ce(t)) T of (10), , , and as t → ∞. Moreover, and for all t ≥ 0 if and , i = 1,2, where
Lemma 6 (see [34].)Suppose that x(t) ∈ C[Ω × [0, +∞), R+].
-
(I) If there exist σ and positive constants σ0, T such that
() -
for t ≥ T, where Bi(t) are independent standard Brownian motions and βi are constants, 1 ≤ i ≤ n, then one has the following: if σ ≥ 0, then 〈x〉 * ≤ σ/σ0 a.s.; if σ < 0, then lim t→+∞x(t) = 0 a.s.
-
(II) If there exist positive constants σ0, T and σ such that
() -
for t ≥ T, then 〈x〉 * ≥ σ/σ0 a.s.
Lemma 7. If , then the solution y(t) of system (15) obeys
Proof. By Lemma 5,
We are now in the position to prove our main results.
Proof of Theorem 2. Applying Itô’s formula to (3) leads to
(i) It follows from (17) and (33) that
(ii) By the stochastic comparison theorem [40], one can observe that
(iii) Clearly, implies θ1 > r11K1/γ, and then, by Lemma 7,
3. Numerical Simulations
Let us use the famous Milstein method (see, e.g., [41]) to illustrate the analytical results.
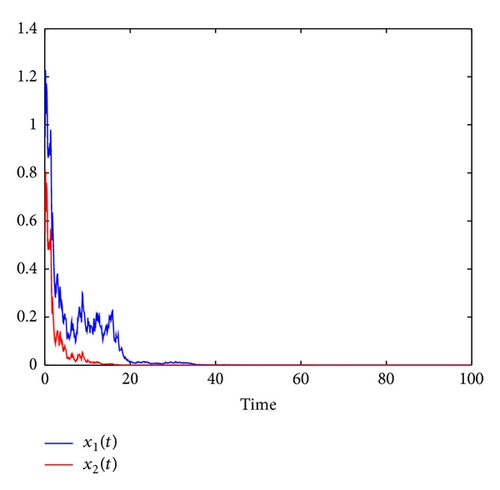
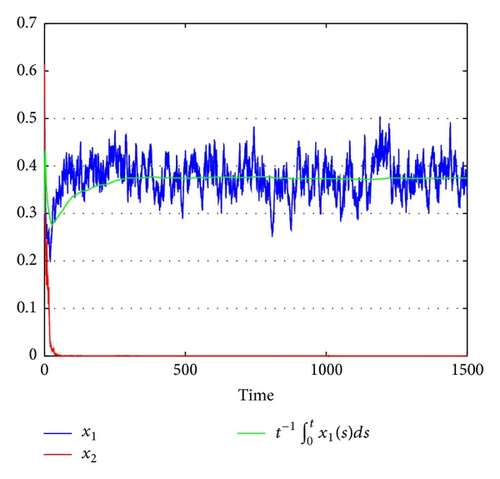

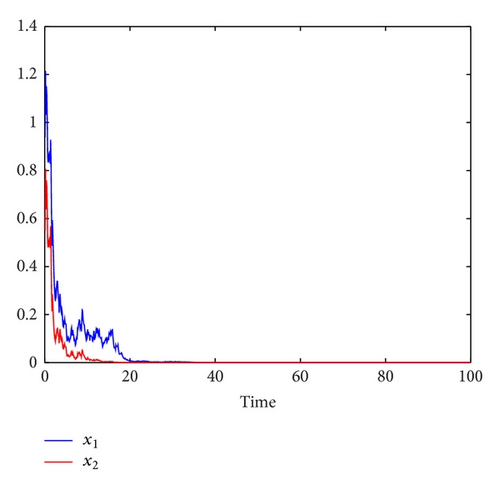
In Figure 2, we choose r10 = 0.85, r20 = 0.05, r11 = r21 = 1, a11 = 0.4, a12 = 0.4, a21 = 0.3, a22 = 0.3, τ1 = 3, τ2 = 8, , , ki = gi = mi = 0.1, i = 1,2, h = 0.5, and b = 0.6. The only difference between conditions of Figures 1(c) and 2 is that the value of γ is different. In Figure 2, we choose γ = 0.8. Then, θ1 = 0.65 < r11K1/γ = 0.75. It follows from (i) in Theorem 2 that both x1 and x2 are extinctive. Figure 2 confirms these. By comparing Figure 1(c) with Figure 2, one can see that the impulsive period γ plays a key role in determining the stability in time average and the extinction of the species.
4. Conclusions and Future Directions
- (A)
Firstly, time delay is harmless for stability in time average and extinction of the stochastic system (3).
- (B)
The white noise α1dB1(t) and α2dB2(t) can change the properties of the system greatly.
- (C)
The impulsive period γ plays an important role in determining the stability in time average and the extinction of the species.
Some interesting questions deserve further investigations. One may consider some more realistic but more complex systems, for example, stochastic delay model with Markov switching (see, e.g., [30, 32, 39]). It is also interesting to investigate what happens if aij is stochastic.
Acknowledgments
The author thanks the editor and reviewer for these valuable and important comments. This research is supported by NSFC of China (nos. 11301207, 11171081, 11301112 and 11171056), Natural Science Foundation of Jiangsu Province (No. BK20130411) and Natural Science Research Project of Ordinary Universities in Jiangsu Province (no. 13KJB110002).




