We propose long-time convergent numerical integration processes for delay differential equations. We first construct an integration process based on modified Laguerre functions. Then we establish its global convergence in certain weighted Sobolev space. The proposed numerical integration processes can also be used for systems of delay differential equations. We also developed a technique for refinement of modified Laguerre-Radau interpolations. Lastly, numerical results demonstrate the spectral accuracy of the proposed method and coincide well with analysis.

1. Introduction

Time delay systems which are described by delay differential equations (DDEs) or more generally functional differential equations (FDEs) have been studied rather extensively in the past thirty years since time delays are often the sources of instability and encountered in various engineering systems such as chemical processes, economic markets, chemical reactions, and population dynamics [1, 2]. Nakagiri [1] studied the structural properties of linear autonomous functional differential equations in Banach spaces within the framework of linear operator theory. The system stability and the compactness of the operators describing the solution trajectories are investigated in [2]. Depending on whether the existence of time delays or not, stability criteria for time delay systems can be divided into two types: delay-dependent ones and delay-independent ones. De la Sen and Luo [3] deal with the global uniform exponential stability independent of delay of time-delay linear and time-invariant systems. By exploiting appropriate Lyapunov functional candidate, new delay-dependent robust stability criteria of uncertain time-delay systems are proposed in [4].

However, most DDEs do not have analytic solution, so it is generally necessary to resort to numerical methods [5, 6]. It is well known that a numerical method which is convergent in a finite interval does not necessarily yield the same asymptotic behavior as the underlying differential equation. If the numerical solution defines a dynamical system, then we would study whether this dynamical system inherits the dynamics of the underlying system. Hence it is crucial to understand the behavior of numerical solution in order that we may interpret the data and facilitate the design of algorithms which provide correct qualitative information without being unduly expensive. The classical analysis of linear multistep methods [7–9] and Runge-Kutta methods [10–12] for delay differential equations involves assessment of stability and accuracy but has also been supplemented by considerable practical experience and experimentation.

As a basic tool, the Runge-Kutta method plays an important role in numerical integrations of delay differential equations. We usually designed this kind of numerical schemes in two ways. The first way is based on Taylor′s expansion coupled with other techniques. The next is to construct numerical schemes by using collocation approximation. For instance, Butcher [13, 14] provided some implicit Runge-Kutta processes based on the Radau Quadrature formulas; also see [15, 16] and the references therein.

Recently, Guo et al. [17] proposed an integration process for ordinary differential equations based on modified Laguerre functions, which are very efficient for long-time numerical simulations of dynamical systems. But so far, to our knowledge, there is no work concerning the applications of Laguerre approximation to integration process for delay differential equations.

In this paper, we construct a new integration processes for delay differential equations based on modified Laguerre functions and establish its global convergence in certain weighted Sobolev space. Numerical results demonstrate the spectral accuracy of the proposed method and coincide well with analysis.

2. Modified Laguerre-Radau Function for Delay Differential Equations

Let ω_β(t) = e^−βt, β > 0, and define the weighted space

as usual, with the following inner product and norm:

()

The modified Laguerre polynomial of degree l is defined by (cf. [18])

()

For example,

()

The modified Laguerre polynomials satisfy the recurrence relation

()

The set of Laguerre polynomials is a complete

-orthogonal system, namely,

()

where δ_l,m is the Kronecker function. Thus, for any

()

Let N be any positive integer and 𝒫_N(0, ∞) the set of all algebraic polynomials of degree at most N. We denote by

the modified Laguerre-Radau interpolation points. Indeed,

, and

are the distinct zeros of

. By using (2.1) and the formula (2.12) of [19], the corresponding Christoffel numbers are as follows:

()

For any ρ ∈ 𝒫_2N(0, ∞),

()

Next, we define the following discrete inner product and norm:

()

For any ϕ, ψ ∈ 𝒫_N(0, ∞),

()

For all

, the modified Laguerre-Radau interpolant I_β,Nv ∈ 𝒫_N(0, ∞) is determined by

()

By (2.10), for any ϕ ∈ 𝒫_N(0, ∞),

()

The interpolant I_β,Nv can be expanded as

()

By virtue of (2.5) and (2.10),

()

Define the modified Laguerre functions

as the base functions. According to (2.4), the functions

satisfy the recurrence relation

()

Denote by (u, v) and ∥v∥ the inner product and the norm of the space L²(0, ∞), respectively. The set of

is a complete L²(0, ∞)-orthogonal system, that is,

()

We now introduce the new Laguerre-Radau interpolation. Set

()

Let

and

be the same as in (2.7), and take the nodes and weights of the new Laguerre-Radau interpolation as

()

The discrete inner product and norm can be defined similarly as

()

For any ϕ₁, ϕ₂ ∈ Q_N(0, ∞), we have ϕ₁ = e^−(1/2)βtψ₁, ϕ₂ = e^−(1/2)βtψ₂, and ψ₁, ψ₂ ∈ 𝒫_N(0, ∞). Thus by (2.10),

()

The new Laguerre-Radau interpolant

is determined by

()

Due to the equality (2.20), for any ϕ ∈ Q_N(0, ∞),

()

Let

()

Then, with the aid of (2.16) and (2.22), we derive that

()

There is a close relation between I_β,N and

. From the previous two equalities, it follows that

()

This with (2.14) implies

()

Consider the following delay differential equation:

()

For any fixed positive integer N, we define

()

and denote

()

Then system of (2.27) can be transformed into

()

We suppose that U(t) is sufficiently continuously differentiable for t ≥ 0. Let

()

Then we obtain that

()

Now we derive an explicit expression for the left side of (2.32). Let

be the coefficients of

in terms of

. Due to (2.15), we have

()

This equality and (2.24) imply that

()

Denote for 0 ≤ j ≤ N and 1 ≤ k ≤ N

()

Then

()

Denote

()

Then, we obtain

()

We now approximate U(t) by u^N(t) ∈ Q_N(0, ∞). Clearly,

. Furthermore, we set

()

By replacing 𝕌^N by u^N and neglecting

in (2.38), we derive a new integration process by using the modified Laguerre functions. It is to seek u^N such that

()

The global numerical solution is

()

with

()

Let

()

Then (2.40) is equivalent to the system

()

3. Convergence Analysis

In this section, we estimate the global error of numerical solution. For any rth continuously differentiable function v(t), we set

()

The following lemmas will play a key role in obtaining our main results.

Lemma 3.1 (see [19].)If , then for an integer r ≥ 1,

()

Lemma 3.2 (see [19].)If , then for an integer r ≥ 1,

()

Theorem 3.3. Suppose that there exists a real number γ₀ > 0 such that

()

and

, and

are finite. Then

()

Proof. Let . Subtracting (2.32) from (2.44), we get

()

where

()

We now multiply (3.7) by

and sum the result for 1 ≤ k ≤ N. Due to E^N(0) = 0, we obtain that

()

where

()

Using (2.20) and the Cauchy inequality, we deduce that

()

Thus (3.9) reads

()

Since there exists γ₀ > 0 such that

()

where

. Therefore

()

Hence it suffices to estimate

. With the aid of (2.26), Lemmas 3.1 and 3.2, we deduce that, for r ≥ 1,

()

On the other hand,

()

It follows from the above result that for r ≥ 1

()

Consequently,

()

Thus, (3.14) implies that

()

Furthermore, using (3.15) again, we obtain that, for any β > 0,

()

This completes the proof.

Remark 3.4. The norm ∥U∥ is finite as long as that f(u, v) satisfies certain conditions. If f(u, v) satisfies conditions

()

and f(0,0) = 0, then

, γ_* > 0, see Tian [5]. Furthermore, if f(u, v) fulfills some additional conditions, then the norms appearing at the right sides of (3.20) are finite. Therefore, for certain positive constant c_* depending only on β,

()

Consequently, for r > 1, the scheme (2.40) has the global convergence and the spectral accuracy in L²(0, ∞). Moreover, at the infinity, the numerical solution has the same accuracy. This also indicates that the pointwise numerical error decays rapidly as the mode N increases, with the convergence rate as c_*(ln N) ^1/2N^1/2−r/2. On the other hand, for any fixed N, the norm

is bounded, and so the pointwise numerical error decays automatically as t → ∞, at least less than c_Nt^−1/2, c_N being a small number. Hence, it is very efficient for long-time numerical simulations of dynamical systems, especially for stiff problems.

Remark 3.5. The method proposed is also available for solving systems of delay differential equations. Let

()

We consider the system

()

We approximate

. We can derive a numerical algorithm which is similar to (2.38). Further, let

be the Euclidean norm of

. Assume that

()

Then we can obtain an error estimate similar to (3.20).

4. Refinement and Numerical Results

In the preceding sections, we introduced an integration process for solving delay differential equations. Theoretically, their numerical errors with bigger N decrease faster. But in practical computation, it is not convenient to use them with very big N. On the other hand, the distance between the adjacent interpolation nodes and increases fast as N and j increase, especially for the nodes which are located far from the origin point t = 0. This is one of advantages of the Laguerre interpolation approximation, since we can use moderate mode N to evaluate the unknown function at large t, but it is also its shortcoming. In fact, if the exact solution oscillates or changes very rapidly between two large adjacent interpolation nodes, then we may lose information about the structure of exact solution between those nodes. To remedy this deficiency, we may refine the numerical results as follows.

Let N be a moderate positive integer, β > 0, and the set of nodes

. We use (2.40) with the interpolation nodes

to obtain the original numerical solution

()

Then we take

and consider the following delay differential equation:

()

We get the refined numerical solution u^(1,N)(t) for

. Repeating the above procedure, we obtain the refined numerical solution u^(m,N)(t) for

5. Numerical Results

We consider the following system of four homogeneous delay differential equations:

()

The initial functions and solutions are given by

()

For n = 1, Figures 1 and 2 show plots of the exact solution y₁(t) and y₃(t) on [0,2π], which controls the frequency of oscillation in the initial data and solution. Figures 3 and 4 are the exact and numerical solution on [0, π] with N = 15, β = 10. The refined numerical results are given in Figures 5 and 6 on [0,3π].

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Exact solution.

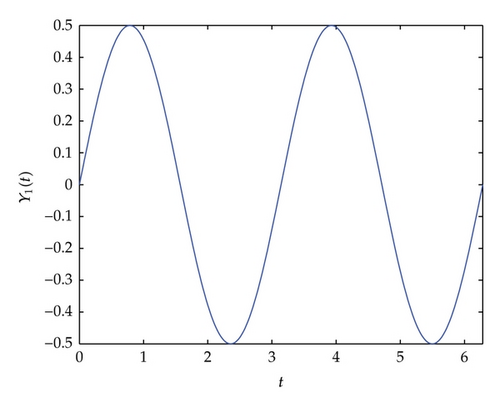
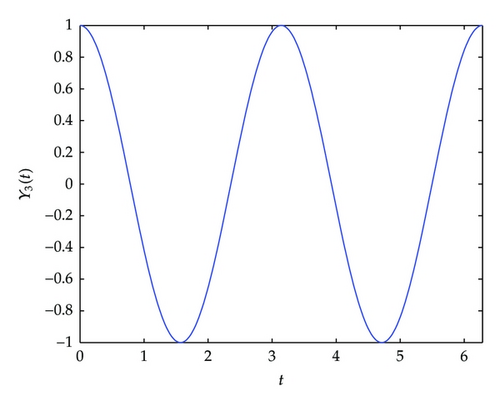
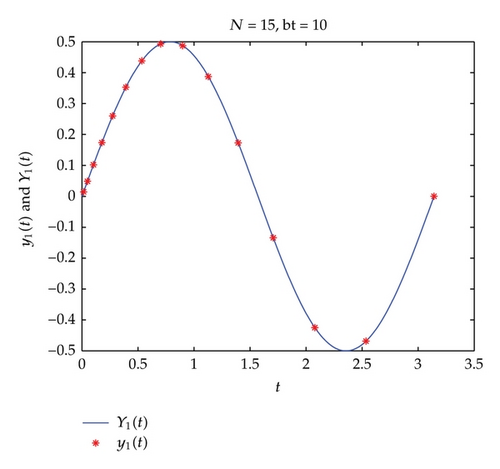
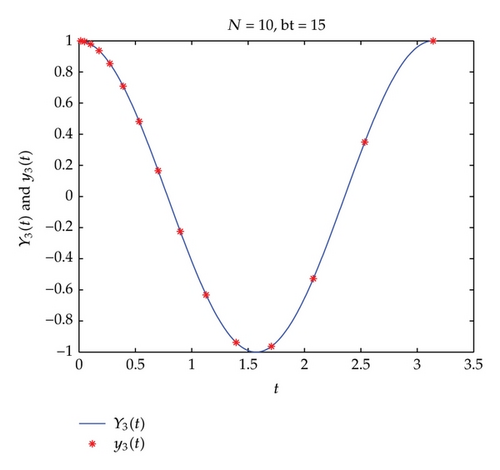
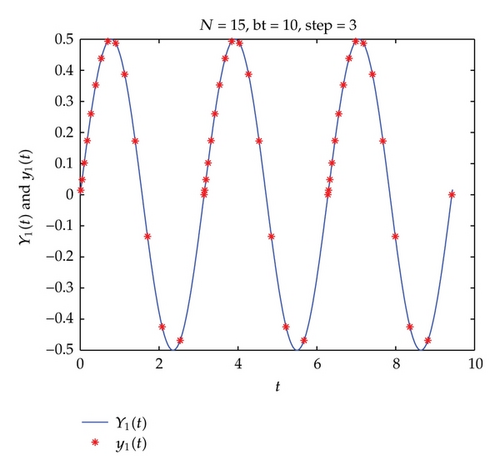
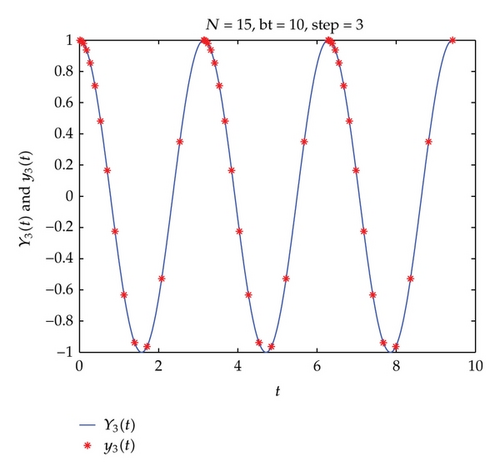
The numerical experiments show that our numerical integration processes are efficient for numerically solving delay differential equations.

6. Conclusions

In this paper, we proposed new integration processes of delay differential equations, which have fascinating advantages. On the one hand, the suggested integration processes are based on the modified Laguerre functions on the half line; they provide the global numerical solution and the global convergence naturally and thus are available for long-time numerical simulations of dynamical systems. On the other hand, benefiting from the rapid convergence of the modified Laguerre functions, these processes possess the spectral accuracy. In particular, the numerical results fit the exact solutions well at the interpolation nodes. Furthermore, We also developed a technique for refinement of modified Laguerre-Radau interpolations. Lastly, numerical results demonstrate the spectral accuracy of the proposed method and coincide well with analysis.

Acknowledgments

This work is supported by the Program of Science and Technology of Huainan no. 2011A08005. The authors wish to thank the anonymous referees for carefully correcting the preliminary version of the paper. Special and warm thanks are addressed to Professor Ram N. Mohapatra for his valuable comments and suggestions for improving this paper.

References

1 Nakagiri S. I., Structural properties of functional-differential equations in Banach spaces, Osaka Journal of Mathematics. (1988) 25, no. 2, 353–398, 957869, ZBL0713.34069.
Web of Science® Google Scholar
2 De la Sen M., Stability of impulsive time-varying systems and compactness of the operators mapping the input space into the state and output spaces, Journal of Mathematical Analysis and Applications. (2006) 321, no. 2, 621–650, https://doi.org/10.1016/j.jmaa.2005.08.038, 2241144, ZBL1111.93072.
10.1016/j.jmaa.2005.08.038
Web of Science® Google Scholar
3 De la Sen M. and Luo N., On the uniform exponential stability of a wide class of linear time-delay systems, Journal of Mathematical Analysis and Applications. (2004) 289, no. 2, 456–476, https://doi.org/10.1016/j.jmaa.2003.08.048, 2026918, ZBL1046.34086.
10.1016/j.jmaa.2003.08.048
Web of Science® Google Scholar
4 Wang C. and Shen Y., Improved delay-dependent robust stability criteria for uncertain time delay systems, Applied Mathematics and Computation. (2011) 218, no. 6, 2880–2888, https://doi.org/10.1016/j.amc.2011.08.031, 2838191, ZBL1241.93037.
10.1016/j.amc.2011.08.031
Web of Science® Google Scholar
5 Tian H. J., The exponential asymptotic stability of singularly perturbed delay differential equations with a bounded lag, Journal of Mathematical Analysis and Applications. (2002) 270, no. 1, 143–149, https://doi.org/10.1016/S0022%2D247X(02)00056%2D2, 1911756, ZBL1014.34062.
10.1016/S0022-247X(02)00056-2
Web of Science® Google Scholar
6 Xu Y., Zhao J. J., and Sui Z. N., Stability analysis of exponential Runge-Kutta methods for delay differential equations, Applied Mathematics Letters. (2011) 24, no. 7, 1089–1092, https://doi.org/10.1016/j.aml.2011.01.029, 2784163, ZBL1214.65042.
10.1016/j.aml.2011.01.029
Web of Science® Google Scholar
7 Huang C. M., Asymptotic stability of multistep methods for nonlinear delay differential equations, Applied Mathematics and Computation. (2008) 203, no. 2, 908–912, https://doi.org/10.1016/j.amc.2008.04.003, 2459009, ZBL1161.65063.
10.1016/j.amc.2008.04.003
Web of Science® Google Scholar
8 Huang C. M., Stability of linear multistep methods for delay integro-differential equations, Computers & Mathematics with Applications. (2008) 55, no. 12, 2830–2838, https://doi.org/10.1016/j.camwa.2007.09.005, 2401434, ZBL1142.65380.
10.1016/j.camwa.2007.09.005
Web of Science® Google Scholar
9 Hu P., Huang C. M., and Wu S. L., Asymptotic stability of linear multistep methods for nonlinear neutral delay differential equations, Applied Mathematics and Computation. (2009) 211, no. 1, 95–101, https://doi.org/10.1016/j.amc.2009.01.028, 2517664.
10.1016/j.amc.2009.01.028
Web of Science® Google Scholar
10 Wang W.-S. and Li S. F., Conditional contractivity of Runge-Kutta methods for nonlinear differential equations with many variable delays, Communications in Nonlinear Science and Numerical Simulation. (2009) 14, no. 2, 399–408, https://doi.org/10.1016/j.cnsns.2007.09.006, 2458817, ZBL1221.65168.
10.1016/j.cnsns.2007.09.006
Web of Science® Google Scholar
11 Yu Y. X., Wen L. P., and Li S. F., Nonlinear stability of Runge-Kutta methods for neutral delay integro-differential equations, Applied Mathematics and Computation. (2007) 191, no. 2, 543–549, https://doi.org/10.1016/j.amc.2007.02.114, 2385556, ZBL1193.65123.
10.1016/j.amc.2007.02.114
Web of Science® Google Scholar
12 Wen L. P., Yu Y. X., and Li S. F., Dissipativity of Runge-Kutta methods for Volterra functional differential equations, Applied Numerical Mathematics. (2011) 61, no. 3, 368–381, https://doi.org/10.1016/j.apnum.2010.11.002, 2754565, ZBL1215.65131.
10.1016/j.apnum.2010.11.002
Web of Science® Google Scholar
13 Butcher J. C., Implicit Runge-Kutta processes, Mathematics of Computation. (1964) 18, 50–64, 0159424, https://doi.org/10.1090/S0025%2D5718%2D1964%2D0159424%2D9, ZBL0123.11701.
10.1090/S0025-5718-1964-0159424-9
Web of Science® Google Scholar
14 Butcher J. C., Integration processes based on Radau quadrature formulas, Mathematics of Computation. (1964) 18, 233–244, 0165693, https://doi.org/10.1090/S0025%2D5718%2D1964%2D0165693%2D1, ZBL0123.11702.
10.1090/S0025-5718-1964-0165693-1
Web of Science® Google Scholar
15 Hairer E., Norsett S. P., and Wanner G., Solving Ordinary Differential Equations I: Nonstiff Problems, 1987, 8, Springer, Berlin, Germany, Springer Series in Computational Mathematics, 868663.
10.1007/978-3-662-12607-3
Google Scholar
16 Hairer E. and Wanner G., Solving Ordinary Differential Equations II: Stiff and Differential-Algebraic Problems, 1991, 14, Springer, Berlin, Germany, Springer Series in Computational Mathematics, 1111480.
10.1007/978-3-662-09947-6
Google Scholar
17 Guo B. Y., Wang Z. Q., Tian H. J., and Wang L. L., Integration processes of ordinary differential equations based on Laguerre-Radau interpolations, Mathematics of Computation. (2008) 77, no. 261, 181–199, https://doi.org/10.1090/S0025%2D5718%2D07%2D02035%2D2, 2353948, ZBL1127.65047.
10.1090/S0025-5718-07-02035-2
Web of Science® Google Scholar
18 Guo B. Y. and Zhang X. Y., A new generalized Laguerre spectral approximation and its applications, Journal of Computational and Applied Mathematics. (2005) 181, no. 2, 342–363, https://doi.org/10.1016/j.cam.2004.12.008, 2146844, ZBL1080.65097.
10.1016/j.cam.2004.12.008
Web of Science® Google Scholar
19 Guo B. Y., Wang L. L., and Wang Z. Q., Generalized Laguerre interpolation and pseudospectral method for unbounded domains, SIAM Journal on Numerical Analysis. (2006) 43, no. 6, 2567–2589, https://doi.org/10.1137/04061324X, 2206448, ZBL1116.41002.
10.1137/04061324X
Web of Science® Google Scholar

All articles

Integration Processes of Delay Differential Equation Based on Modified Laguerre Functions

Abstract

1. Introduction

2. Modified Laguerre-Radau Function for Delay Differential Equations

3. Convergence Analysis

4. Refinement and Numerical Results

5. Numerical Results

6. Conclusions

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Integration Processes of Delay Differential Equation Based on Modified Laguerre Functions

Abstract

1. Introduction

2. Modified Laguerre-Radau Function for Delay Differential Equations

3. Convergence Analysis

4. Refinement and Numerical Results

5. Numerical Results

6. Conclusions

Acknowledgments

References

Figures

References

Related

Information