Matroidal Structure of Rough Sets from the Viewpoint of Graph Theory
Abstract
Constructing structures with other mathematical theories is an important research field of rough sets. As one mathematical theory on sets, matroids possess a sophisticated structure. This paper builds a bridge between rough sets and matroids and establishes the matroidal structure of rough sets. In order to understand intuitively the relationships between these two theories, we study this problem from the viewpoint of graph theory. Therefore, any partition of the universe can be represented by a family of complete graphs or cycles. Then two different kinds of matroids are constructed and some matroidal characteristics of them are discussed, respectively. The lower and the upper approximations are formulated with these matroidal characteristics. Some new properties, which have not been found in rough sets, are obtained. Furthermore, by defining the concept of lower approximation number, the rank function of some subset of the universe and the approximations of the subset are connected. Finally, the relationships between the two types of matroids are discussed, and the result shows that they are just dual matroids.
1. Introduction
Rough sets provide an important tool to deal with data characterized by uncertainty and vagueness. Since it was proposed by Pawlak [1, 2], rough sets have been generalized from different viewpoints such as the similarity relation [3, 4] or the tolerance relations [5] instead of the equivalence relation, and a covering over the universe instead of a partition [6–10], and the neighborhood instead of the equivalence class [11–14]. Besides, using some other mathematical theories, such as fuzzy sets [15–19], boolean algebra [20–23], topology [24–27], lattice theory [28–30], and modal logic [31], to study rough sets has became another kind of important generalizations of rough sets. Specially, matroids also have been used to study rough sets recently [32, 33].
Matroids, as a simultaneous generalization of graph theory and linear algebra, was proposed by Whitney in [34]. The original purpose of this theory is to formalize the similarities between the ideas of independence and rank in graph theory and those of linear independence and dimension in the study of vector spaces [35]. It has been found that matroids are effective to simplify various ideas in graph theory and are useful in combinatorial optimization problems.
In the existing works on the combination of rough sets and matroids, Zhu and Wang [32] constructed a matroid by defining the concepts of upper approximation number in rough sets. Then they studied the generalized rough sets with matroidal approaches. As a result, some unique properties are obtained in this way. Wang et al. [33] studied the covering-based rough sets with matroids. Two matroidal structures of covering-based rough sets are established.
In this paper, we attempt to make a further contribution to studying rough sets with matroids. As we see in Section 2.3, it is somewhat hard to understand matroids. And this will also arise in the combination of matroids and rough sets. So, in order to give an intuitive interpreting to the combination, we will study it from the viewpoint of graph theory. There are at least two kinds of graphic ways, which can be used to build relationships between matroids and rough sets. The complete graph and the cycle. More specifically, for a partition over the universe, any equivalence class of the partition can be regarded as a complete graph or a cycle. Thus a partition is transformed to a graph composed of these complete graphs or circles induced by the equivalence classes of the partition. And we can establish a matroid in terms of the graph. Afterwards, some characteristics of the matroid are formulated and some new properties, which are hard to be found via the rough sets way, are obtained. With these characteristics and properties, a matroidal structure of rough sets is constructed. Finally, the relationships between the two kinds of matroids established from the viewpoints of complete graph and cycle are discussed.
The rest of this paper is organized as follows. In Section 2, we review some basic knowledge about rough sets, matroids, and graph theory. In Section 3, we analyze the relationships between rough set theory and graph theory from the viewpoints of complete graph and cycle, respectively. In Sections 4 and 5, two kinds of matroids are established in terms of the analytical results of Section 3. And two kinds of the matroidal structures of rough sets are constructed. In Section 6, the relationships between the two kinds of matroids are discussed.
2. Preliminary
For a better understanding to this paper, in this section, some basic knowledge of rough sets, graph theory, and matroids are introduced.
2.1. Rough Sets
Let U be a nonempty and finite set called universe, R a family of equivalence relations over U, then the relational system K = (U, R) is called a knowledge base [1]. If ∅ ≠ Q⊆R, then ∩Q is also an equivalence relation [1]. And ∩Q is called an indiscernibility relation and denoted by IND(Q) [1]. If R ∈ R, then U/R represents the partition of U induced by R. That is in the partition U/R = {T1, T2, …, Tn}, for all Ti ∈ U/R, Ti⊆U and Ti ≠ ∅, Ti ∩ Tj = ∅ for i ≠ j, i, j = 1,2, …, n, and ∪Ti = U. Each Ti in U/R is an equivalence class, and it can also be denoted by [x] R if x ∈ Ti.
- (P1)
for all X⊆U, ,
- (P2)
for all X⊆U, ,
Neighborhood and upper approximation number are another two important concepts, which will be used in this paper. They are defined as follows.
Definition 2.1 (Neighborhood [36]). Let R be a relation on U. For all x ∈ U, RNR(x) = {y ∈ U : xRy} is called the successor neighborhood of x in R. When there is no confusion, we omit the subscript R.
Definition 2.2 (Upper approximation number [32]). Let R be a relation on U. For all X⊆U, is called the upper approximation number of X with respect to R.
2.2. Graph Theory
A graph G is an ordered pair of disjoint sets (V, E) such that E is a subset of the set V(2) of unordered pairs of V [37]. The set V is the set of vertices and E is the set of edges. If G is a graph, then V = V(G) is the vertex set of G, and E = E(G) is the edge set. An empty graph is a graph whose edge set is empty. An edge {u, v} is said to join the vertices u and v and is denoted by uv. Thus uv and vu mean exactly the same edge; the vertices u and v are the endpoints of this edge. If uv ∈ E(G), then u and v are adjacent and are neighbors. A loop [38] is an edge whose endpoints are equal. Parallel edges are edges having the same pair of endpoints. The degree of vertex v in a graph G, denoted by dG(v) or d(v), is the number of edges incident to v, except that each loop at v counts twice.
A simple graph is a graph having no loops or parallel edges [38]. An isomorphism [38] from a simple graph G to a simple graph H is a bijection f : V(G) → V(H) such that uv ∈ E(G) if and only if f(u)f(v) ∈ E(H). That is to say “G is isomorphic to H,” denoted by G≅H if there is an isomorphism from G to H.
We say that G′ = (V′, E′) is a subgraph of G = (V, E) if V′ ⊂ V and E′ ⊂ E [37]. In this case, we write G′ ⊂ G. If G′ contains all edges of G that join two vertices in V′ then G′ is said to be the subgraph induced by V′ and is denoted by G[V′]. Thus, a subgraph G′ of G is an induced subgraph if G′ = G[V(G′)].
2.3. Matroids
Definition 2.3 (Matroid [39]). A matroid M is a pair (E, ℐ), where E (called the ground set) is a finite set and ℐ (called the independent sets) is a family of subsets of E satisfying the following axioms:
-
I1 ∅ ∈ ℐ;
-
I2 if I ∈ ℐ and I′⊆I, then I′ ∈ ℐ;
-
I3 if I1, I2 ∈ ℐ and |I1 | <|I2|, then ∃e ∈ I2 − I1 such that I1 ∪ {e} ∈ ℐ,
Example 2.4. Let E = {a, b, c}, ℐ = {{a, b}, {b, c}, {a}, {b}, {c}, ∅}. Then (E, ℐ) is a matroid, which satisfies the axioms (I1)~(I3). And each element of ℐ is an independent set. {a, b, c} and {a, c} are only two dependent sets of (E, ℐ).
Next, we will introduce some characteristics of a matroid. For a better understanding to them, some operations will be firstly introduced as follows.
Definition 2.5 (Circuit [39]). Let M be a matroid. A minimal dependent set is called a circuit of M, and the set of all circuits of M is denoted by 𝒞(M), that is, 𝒞(M) = Min (Opp(ℐ)).
A circuit in a matroid M(E, ℐ) is a set which is not independent but has the property that every proper subset of it is independent. In Example 2.4, 𝒞(M) = {{a, c}}.
Theorem 2.6 (Circuit axioms [39]). Let 𝒞 be a family of subsets of E. Then there exists M(E, ℐ) such that 𝒞 = 𝒞(M) if and if only 𝒞 satisfies the following properties:
-
C1 ∅ ∉ 𝒞;
-
C2 if C1, C2 ∈ 𝒞 and C1⊆C2, then C1 = C2;
-
C3 if C1, C2 ∈ 𝒞, C1 ≠ C2, and ∃e ∈ C1∩C2, then ∃C3 ∈ 𝒞 such that C3⊆(C1 ∪ C2)−{e}.
Definition 2.7 (Base [39]). Let M be a matroid. A maximal independent set of M is called a base of M; the set of all bases of M is denoted by ℬ(M), that is, ℬ(M) = Max (ℐ).
In Example 2.4, according to Definition 2.7, we can get that ℬ(M) = {{a, b}, {b, c}}.
It is obvious that all bases of a matroid have the same cardinality, which is called the rank of the matroid.
Definition 2.8 (Rank function [39]). Let M = M(E, ℐ) be a matroid. Then the rank function rM of M is defined as: for all X⊆E,
A matroid can be determined by its base, its rank function, or its circuit. For a set, I⊆E is independent if and only if it is contained in some base, if and only if it satisfies rM(I) = |I|, or if and only if it contains no circuit. It is possible to axiomatize matroids in terms of their sets of bases, their rank functions, or their sets of circuits [40].
Definition 2.9 (Closure [39]). Let M = M(E, ℐ) be a matroid. For all X⊆E, the closure operator cl M of M is defined as follows:
If e ∈ cl M(X), we say that e depends on X. The closure of X is composed of these elements of E that depend on X. If cl M(X) = X, then X is called a closed set of M.
Definition 2.10 (Hyperplane [39]). Let M = (E, ℐ) be a matroid. H⊆E is called a hyperplane of M if H is a closed set of M and rM(H) = rM(E) − 1. And ℋ(M) represents the family of all hyperplanes of M.
3. The Viewpoint of Graph Theory in Rough Sets
Graph theory provides an intuitive way to interpret and comprehend a number of practical and theoretical problems. Here, we will make use of it to interpret rough sets. There are at least two different ways to understand rough sets from the viewpoint of graph theory: the complete graph and the cycle. This will be analyzed in detail in the following subsections.
3.1. The Complete Graph
Definition 3.1 (Complete graph [38]). A complete graph is a simple undirected graph whose vertices are pairwise adjacent. A complete graph whose cardinality of vertex set is equal to n is denoted by Kn.
In rough sets, an equivalence relation can generally be regarded as an indiscernibility relation. That means any two different elements in the same equivalence class are indiscernible. In order to interpret this phenomenon from the viewpoint of graph theory, we can consider the two elements as two vertices and the indiscernibility relation between them as an edge connecting the two vertices. Then an equivalence class is represented by a complete graph. For a better understanding of it, an example is served as follows.
Example 3.2. Let U = {a, b, c, d, e, f, g, h} be the universe, R an equivalence relation, and U/R = {T1, T2, T3} = {{a}, {b, c}, {d, e, f, g, h}}. Then each equivalence class can be transformed to a complete graph showed in Figure 1.
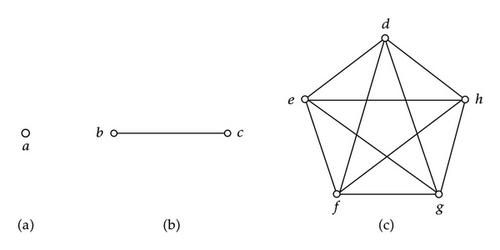
Figure 1(a) represents the complete graph of the equivalence class T1. Because T1 just includes one element a, there is only one vertex and no edge in the complete graph Figure 1(a). Figure 1(b) represents the complete graph of T2, which includes two vertices and only one edge connecting the two vertices. And Figure 1(c) represents the complete graph of T3. We can find that there are five vertices in Figure 1(c) and each pair of vertices are connected by an edge. Here, we denote the complete graphs Figures 1(a), 1(b), and 1(c) as , , and , respectively.
3.2. The Cycle
A walk [37] W in a graph is an alternating sequence of vertices and edges, say x0, e1, x1, e2, …, el, xl where ei = x(i−1)xi, 0 < i ≤ l. For simplicity, the walk W can also be denoted by x0x1 ⋯ xl; the length of W is l, that is, the number of its edges. A walk that starts and ends at the same vertex but otherwise has no repeated vertices is called a cycle [41]. A cycle on one vertex consists of a single vertex with a loop, and a cycle on two vertices consists of two vertices joined by a pair of parallel edges [42].
Then, how to build a bridge between rough sets and cycle? In rough sets, elements contained in the same equivalence class are indiscernible, and any proper subset of an equivalence class is no longer an equivalence class. So, we can convert an equivalence class to a cycle whose vertices set is the equivalence class. Therefore, each vertex is connected with all vertices in the cycle [42]. This reflects the indiscernible relationship among the elements of an equivalence class. Furthermore, any subgraph of the cycle does not contain a cycle. That is, any subgraph of the cycle is no longer a cycle. This can be illustrated in the following example.
Example 3.3 (Continued from Example 3.2). For any equivalence class in U/R, it can be represented by a cycle. As shown in Figure 2, the equivalence class T1, T2, and T3 are represented by Figures 2(a), 2(b), and 2(c), respectively.
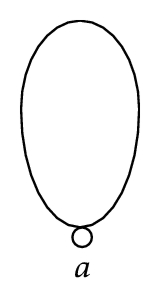
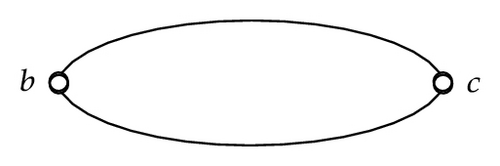
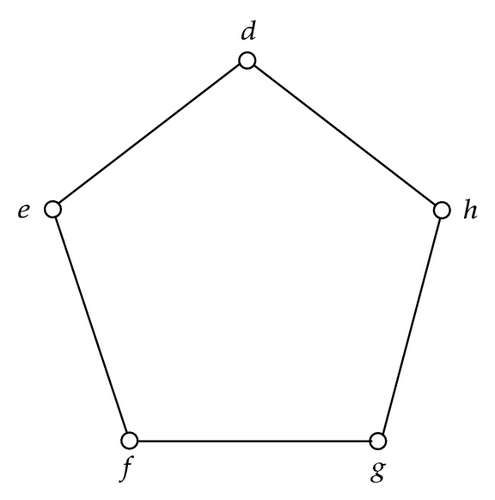
Figure 2(a) is a cycle with only one vertex and one edge. It is also called a loop. That means the vertex a is connected with itself. Figure 2(b) is a cycle with two vertices and two edges. And it is generally regarded as a parallel edges. Figure 2(c) is not only a cycle but also a simple graph. Obviously, any subgraph of each cycle in Figure 2 is no longer a cycle. And, for any two different elements of the universe, they belong to the same equivalence class if and only if they are connected to each other.
It is worth noting that the sequence of vertices in a cycle is not emphasized here. We only care that the vertices, namely, elements of some equivalence class, can form a cycle. So, to Figure 2(c), the cycle defghd and cycle dfhegd can be treated as the same cycle.
One may ask which edges belong to ET exactly? In fact, it is nonnecessary to define the edges of ET exactly. Here, we just need to form a cycle with the vertex set T. That is, each pair of vertices of T are connected and the degree of each vertex is equal to 2. In other words, we simply need to know that each vertex of CT is adjacent with two other vertices (except the loop and parallel edges) and do not need to care which two vertices they are.
So far, rough sets are interpreted from the viewpoints of complete graph and cycle, respectively. The above analysis shows that there are some similarities, and also some differences, between the two ways to illustrate rough sets. Because there are closed connections between graph theory and matroid theory, we will study the matroidal structure of rough sets through the two kinds of graphs.
4. Matroidal Structure of Rough Sets Constructed from the Viewpoint of Complete Graph
In Section 3, we discussed rough sets from the viewpoint of graph theory. Two graphic ways are provided to describe rough sets. In this section, we will construct two types of matroidal structures of rough sets. One of them is established by using the principle of complete graph and the other of cycle.
For convenience, in this section, we suppose that U is the universe, R an equivalence relation over U and P = U/R the partition. And GP = (U, EP) is the graph induced by P, where EP = {xy : x ∈ T ∈ P∧y ∈ T − {x}}.
4.1. The First Type of Matroidal Structure of Rough Sets
We know that a complete graph is a simple graph. Then, for any vertex v of a complete graph, there is not a loop whose vertex is v. That is to say there is not an edge between a vertex and itself. Furthermore, for any two vertices coming from different complete graphs, there is not an edge between them as well. Because an equivalence class can be represented by a complete graph, we can construct the matroidal structure of rough sets from this perspective.
In this subsection, the first type of matroid induced by a partition will be established and defined. And then some characteristics of it such as the base, circuit, rank function, and closure are studied.
Proposition 4.1. Let ℐP = {X⊆U : GP[X] is an empty graph}. Then there is a matroid M on U such that ℐ(M) = ℐP.
Proof. According to Definition 2.3, we just need to prove that ℐP satisfies axioms (I1)~(I3). It is obvious that (I1) and (I2) hold. Suppose that X, Y ∈ ℐP and |X | <|Y|. Because GP[X] and GP[Y] are empty graphs, according to the definition of EP, each x ∈ X belongs to a different equivalence class with the others of X and the same to each y ∈ Y. Since |X | <|Y|, thus there must be at least one element y0 ∈ Y such that y0 belongs to some equivalence class which does not include any element of X. Therefore, X ∪ {y0} ∈ ℐP. As a result, ℐP satisfies (I3). That is, there exists a matroid M on U such that ℐ(M) = ℐP.
Definition 4.2 (The first type of matroid induced by a partition). The first type of matroid induced by a partition P over U, denoted by I-MIP, is such a matroid whose ground set E = U and independent sets ℐ = {X⊆U : GP[X] is an empty graph}.
Obviously, matroids proposed in Proposition 4.1 is a I-MIP. From the above result of ℐP, we can find that any two elements of X come from different equivalence class. Therefore, we can get the following proposition.
Proposition 4.3. Let MP = (U, ℐP) be an I-MIP. Then for all X⊆U, X ∈ ℐP if and only if for all T ∈ P such that |X∩T | ≤ 1.
Proof. (⇒): If X ∈ ℐP, then GP[X] is an empty graph. According to the definition of EP, each element of X comes from a different equivalence class with the others of X. That is, for all T ∈ P, |X∩T | ≤ 1.
(⇐): Let X⊆U. If for all T ∈ P, |X∩T | ≤ 1, then GP[X] is an empty graph. Therefore, X ∈ ℐP.
A matroid can be determined by its base, its rank function, or its circuit. So it is possible to axiomatize matroids in terms of their sets of bases, their rank functions, or their sets of circuits [40]. Here we will axiomatize the I-MIP in terms of its circuit.
Theorem 4.4. Let M be a matroid induced by P. Then M is an I-MIP if and only if for all C ∈ 𝒞(M), |C | = 2.
Proof. According to Definition 2.3, we know that ℐ(M)⊆2U. If ℐ(M) = 2U, then M is a I-MIP induced by P = {{x} : x ∈ U}. In this case, according to (2.2), 𝒟(M) = ∅ and 𝒞(M) = ∅. It indicates that there is not any circuit in 𝒞(M), and, therefore, we do not need to care whether the cardinality of each circuit of 𝒞(M) is equal to 2. That is, 𝒞(M) = ∅ is compatible with the description that for all C ∈ 𝒞(M), |C | = 2. Similarly, if 𝒞(M) = ∅, then M is a I-MIP induced by P = {{x} : x ∈ U}. So, Theorem 4.4 is true when the set of circuits of M is empty.
Next, we prove that Theorem 4.4 is true when the set of circuits of M is nonempty.
(⇒): According to (2.2), 𝒟(M) = 2U − ℐP. Therefore, in terms of Definition 4.2 and Proposition 4.1, for all X⊆U, X ∈ 𝒟(M) if and only if GP[X] is not an empty graph. That is, there is at least one edge in GP[X]. Obviously, the set of endpoints of each edge of GP[X] is a dependent set. So, for all X ∈ 𝒟(M), there is a set Y composed of the endpoints of some edge of GP[X] such that Y⊆X. According to Definition 2.5, Y ∈ 𝒞(M) and X ∉ 𝒞(M). That is, for all C ∈ 𝒞(M), |C | = 2.
(⇐): 𝒟(M) = {X⊆U : ∃C ∈ 𝒞(M) s.t. C⊆X}. According to (2.2), ℐ(M) = 2U − 𝒟(M). Therefore, for all I ∈ ℐ(M), ∄C ∈ 𝒞(M) such that C⊆I, that is, for all C ∈ 𝒞(M), |C ∩ I | ≤ 1. So, for all C1, C2 ∈ 𝒞(M); if I ∩ C1 ≠ ∅, then I ∩ C2 = C1 ∩ C2. According to Theorem 2.6, if C1 ∩ C2 ≠ ∅, then ∃C3 ∈ 𝒞(M) such that C3 = C1 ∪ C2 − C1∩C2. For all Ci ∈ 𝒞(M), let . Then . Furthermore, if C1 ∩ C2 = ∅, then . If for all C ∈ 𝒞(M), I ∩ C = ∅, then for all y ∈ I, ∄C ∈ 𝒞(M) such that y ∈ C. Thus, is a partition over U. So ℐ(M) = {I⊆U : for all X ∈ P𝒞(M), | I ∩ X | ≤ 1}. According to Definition 4.2, M = (U, ℐ) is a I-MIP.
Summing up, Theorem 4.4 is true.
In terms of Proposition 4.1, we can get a matroid induced by a partition. Then one may ask whether there is a bijection between a partition and the I-MIP induced by the partition. This question will be answered by the following theorem.
Theorem 4.5. Let 𝒫 be the collection of all partitions over U, ℳ the set of all I-MIP induced by partitions of 𝒫, f : 𝒫 → ℳ, that is, for all P ∈ 𝒫, f(P) = MP, where MP is the I-MIP induced by P. Then f satisfies the following conditions:
- (1)
for all P1, P2 ∈ 𝒫, and if P1 ≠ P2 then f(P1) ≠ f(P2),
- (2)
for all M ∈ ℳ, ∃PM ∈ 𝒫 s.t. f(PM) = M.
Proof. (1) Let P1, P2 ∈ 𝒫, P1 ≠ P2, and , are two I-MIP induced by P1 and P2, respectively. We need to prove that there is an such that , or there is an such that . Because P1 ≠ P2, there is at least one equivalence class T1 ∈ P1 such that T1 ∉ P2. If ∃T2 ∈ P2 such that T1 ⊂ T2, then ∃X⊆U and such that X∩(T2 − T1) ≠ ∅. That means . Else, there at least two equivalence classes T2i, T2j ∈ P2 such that T2i∩T1 ≠ ∅ and T2j∩T1 ≠ ∅. That is, there is a set such that Y∩T2i∩T1 ≠ ∅ and Y∩T2j∩T1 ≠ ∅. Obviously, according to Proposition 4.3, .
(2) Let M = (U, ℐ) be a I-MIP, for all x ∈ U, Cx = {x}∪(∪{C ∈ 𝒞(M) : C∩{x} ≠ ∅}). According to Theorem 4.4, for all y ∈ U and y ∉ Cx, then Cx∩Cy = ∅. Therefore, we can get a family CU = {Cx : x ∈ U}. It is obvious that ∪CU = U. Therefore, CU is a partition of U. That is, CU ∈ 𝒫 and f(CU) = M.
Theorem 4.5 shows that there is one-to-one correspondence between a partition and the I-MIP induced by the partition.
4.2. Characteristics of I-MIP
The characteristics of a matroid are very important to describe the matroid from different aspects. In this subsection, we will study the characteristics of I-MIP such as the base, circuit, rank function, and closure.
The set of bases of a matroid is the collection of all maximal independent sets. Observing from the result of ℐP in Section 4.1, the maximal independent set is the vertex set whose cardinality is equal to the cardinality of P. Then the following proposition can be obtained.
Proposition 4.6. Let MP be the I-MIP induced by P, Y⊆U, and GP[Y] = (Y, EY) a subgraph of GP. Then ℬP = {X⊆U:|X | = |P | ∧EX = ∅} is the set of bases of MP.
Proof. According to Definition 2.7, we need to prove that ℬ(MP) = ℬP, namely, Max (ℐP) = {X⊆U:|X | = |P | ∧EX = ∅}. In terms of Proposition 4.3, for all I ∈ ℐP, |I∩T | ≤ 1 for all T ∈ P. So, for all I ∈ ℬ(MP), |I | = |P|. According to Proposition 4.1 and Definition 4.2, for all I ∈ ℬ(MP), GP[I] is an empty graph, that is, I ∈ ℬP. Similarly, we can prove in the same way that for all X ∈ ℬP, X ∈ ℬ(MP). That is, ℬ(MP) = ℬP.
For a base B in ℬP, we can say that B is such a set including one and only one element of every equivalence class of P. Then we can get the following corollary.
Corollary 4.7. Let X⊆U. Then X ∈ ℬP if and only if for all T ∈ P, |X∩T | = 1.
Proof. According to Proposition 4.6, it is straightforward.
Corollary 4.8. ∪ℬP = U.
Proof. According to Proposition 4.6, it is straightforward.
For a subset X of U, X is either an independent set or a dependent set of MP. And so the opposition to the Proposition 4.1, X is a dependent set if and only if there is at least one pair of vertices of the vertex set of GP[X], which is adjacent. Furthermore, a minimal dependent set of MP is the vertex set of an edge of GP. Then we can get the following proposition.
Proposition 4.9. Let MP = (U, ℐP) be the I-MIP induced by P. Then 𝒞P = {{x, y} : xy ∈ EP} is the set of circuits of MP.
Proof. According to Definition 2.5, we need to prove 𝒞(MP) = 𝒞P, that is, Min (Opp(ℐP)) = {{x, y} : xy ∈ EP}. 𝒟(M) = Opp(ℐP), for all I ∈ 𝒟(M), ∃x, y ∈ I such that xy ∈ E(GP[I]). Furthermore, xy ∈ EP. If {x, y} ⊂ I, then {x, y} ∈ 𝒞(MP) and I ∉ 𝒞(MP); else, {x, y} = I ∈ 𝒞(MP). So, for all I ∈ 𝒞(MP), I ∈ 𝒞P. Similarly, for all {x, y} ∈ 𝒞P, ∃I ∈ 𝒟(MP) such that {x, y}⊆I. Therefore, {x, y} ∈ 𝒞(MP). As a result, 𝒞P = {{x, y} : xy ∈ EP}.
According to Proposition 4.1, it can be found that each subset of U which contains exactly one element is an independent set. So, for any dependent set X of MP, if |X | > 2 then there must exist a subset Y of X such that |Y | = 2 and Y is a dependent set. Thus, we can get the following proposition.
Proposition 4.10. Let MP be the I-MIP induced by P. Then 𝒞+ = {X⊆U : ∃T ∈ P s.t. X⊆T∧|X| = 2} is the set of circuits of MP.
Proof. According to Proposition 4.3, for all X ∈ 𝒞+, X is a dependent set, that is, X ∈ 𝒟(MP). In terms of Proposition 4.9, X ∈ 𝒞(MP). Similarly, for all I ∈ 𝒞(MP), according to Proposition 4.9, I ∈ 𝒞+. That is, 𝒞+ is the set of circuits of MP.
From Propositions 4.9 and 4.10, we can find that 𝒞P and 𝒞+ are the set of circuits of MP. Therefore, we can get the following corollary.
Corollary 4.11. 𝒞P = 𝒞+.
Propositions 4.1 and 4.3 provide two ways to transform an partition to a matroid. Then, how to convert an I-MIP to a partition? In the following proposition, this question is answered through the set of circuits of the I-MIP.
Proposition 4.12. Let MP be the I-MIP induced by P. Then for all x ∈ U,
Proof. According to Proposition 4.10, for all T ∈ P, if x ∈ T then {x, y} ∈ 𝒞(MP) for each y ∈ T − {x}. And for any y ∈ U and y ∉ T, {x, y} ∉ 𝒞(MP). Therefore, T = [x] R = {x}∪{y ∈ U : {x, y} ∈ 𝒞(MP)}.
Proposition 4.12 shows that if two different elements form a circuit, then they belong to the same equivalence class. In terms of (3.2), there is an edge in EP whose vertex set just contains the two elements. For a subset X⊆U, if X does not contain a circuit, then X is an independent set and the rank of it is equal to |X|. In other words, if GP[X] is an empty graph, that is, each pair of vertexes of GP[X] is nonadjacent, then the rank of X is equal to |X|. According to Definition 2.8, for any subset of the universe, the rank of the subset is the number of the maximal independent set contained in the subset. Therefore, we can get the following proposition.
Proposition 4.13. Let MP be the I-MIP induced by P. Then for all X⊆U, rP(X) = max {|Y| : Y⊆X, GP[Y] is an empty graph} is the rank of X in MP.
It can be proved easily that rP(X) = r+(X). So, r+ is also the rank function of MP.
Different from the rank of X in MP, the closure of X is the maximal subset of U, which contains X and its rank is equal to X. For an element y ∈ U − X, if there is an element x ∈ X such that {x, y} form a circuit, then the rank of X is equal to it of X ∪ {y}. That is, y belongs to the closure of X. Therefore, we can get the following proposition.
Proposition 4.14. Let MP be the I-MIP induced by P. Then for all X⊆U, cl P(X) = X ∪ {y ∈ U − X : x ∈ X∧xy ∈ EP} is the closure of X in MP.
Proof. According to Definition 2.9, we need to prove that , that is, . It is obvious that, for all X⊆U, X⊆cl P(X). So, we just need to prove that for all y ∈ U − X if there is an element x ∈ X such that xy ∈ EP if and if only . According to (3.1), xy ∈ EP if and if only x and y belong to the same equivalence. According to Definition 2.8, for all X⊆U, is equal to the number of the maximal independent set contained in X. According to Proposition 4.3, for all X′⊆X; if X′ is a maximal independent set contained in X, then X′ ∪ {y} is not an independent set. That is, . Thus, for all x ∈ U, x ∈ cl P(X) if and if only .
For any element x ∈ U, according to Figure 1, it can be found that if there is an element y ∈ U − {x} such that xy ∈ EP, then x and y must belong to the same equivalence class. Then we can get the following corollary.
Corollary 4.15. Let x ∈ U. For all T ∈ P; if x ∈ T then cl P({x}) = cl P(T).
Next, we will discuss the hyperplane of the I-MIP. From the Definition 2.10, we know that a hyperplane of a matroid is a closed set and the rank of it is one less than the rank of the matroid. Because the rank of the I-MIP induced by P is equal to the cardinality of P, we can get the following proposition.
Proposition 4.16. Let MP be the I-MIP induced by P. Then ℋP = {U − T : T ∈ P} is the hyperplane of MP.
Proof. According to (4.5) and Proposition 4.6, we know that the rank of the I-MIP induced by P is equal to |P|. Furthermore, in terms of Proposition 4.14 and Corollary 4.15, for all T ∈ P, U − T is a closed set and . So U − T ∈ ℋ(MP), that is, for all X ∈ ℋP, X ∈ ℋ(MP). Similarly, we can get that for all X ∈ ℋ(MP), X ∈ ℋP.
4.3. Approximations Established through I-MIP
So far, the base, circuit, rank function, closure, and hyperplane of a I-MIP are established. Next, we will further study the approximations in rough sets in this subsection through these characteristics.
Proposition 4.17. Let MP be the I-MIP induced by P, ℬ(MP) = ℬP. Then for all X⊆U,
Proof. For all B ∈ ℬP, B∩X is an independent set contained in X. Because BX is a base having the maximal intersection with X, . Furthermore, for all y ∈ BX − X, [y] R∩X = ∅. Let S1 = {[y] R : y ∈ BX − X} and S2 = P − S1. Then . If BX − X⊆B, then B − (BX − X)⊆∪S2. According to Corollary 4.7, for all Y⊆∪S2, if for all T ∈ (P − S2) and |Y∩T | = 1, then Y ∪ (BX − X) ∈ ℬP. And ∪{Y⊆∪S2 : for all T ∈ (P − S2), |Y∩T | = 1} = ∪S2. Therefore, ∪S2 = ∪{B − (BX − X) : B ∈ ℬP∧(BX − X)⊆B}. That is, .
In rough sets, an element in the lower approximation certainly belongs to X, while an element in the upper approximation possibly belongs to X [43]. And the boundary region of X is the set of elements in which each element does not certainly belong to either X or ~X. In general, we can get the boundary region of X by the difference set of the lower and upper approximation of X. But here, we can provide a matroidal approach to obtain the boundary region of X firstly, and then the lower and the upper approximations should be established.
Proposition 4.18. Let MP be the I-MIP induced by P, 𝒞(MP) = 𝒞P. Then for all X⊆U,
Proof. According to Proposition 4.10 and Corollary 4.11, for all C ∈ 𝒞P, ∃ T ∈ P such that C⊆T. |C∩X | = 1 means that each element of C does not certainly belong either to X or to ~X. And then ∪{C ∈ 𝒞P:|C∩X | = 1} is the collection of all elements, which do not certainly belong either to X or to ~X. So BNR(X) = ∪{C ∈ 𝒞P:|C∩X | = 1}.
Proposition 4.19. Let MP be the I-MIP induced by P, 𝒞(MP) = 𝒞P. Then for all X⊆U,
Proof. According to the definition of the boundary region and Proposition 4.18, it is straightforward.
Corollary 4.20. Let MP be the I-MIP induced by P, 𝒞(MP) = 𝒞P and X⊆U. Then for all C ∈ 𝒞P, if and only if for all x ∈ X, {x} ∈ P.
Proof. (⇒): According to Proposition 4.10 and Corollary 4.11, if for all , then for all T ∈ P and |T | ≥ 2, T∩X = ∅. That is, for all x ∈ X, {x} ∈ P.
(⇐): It is straightforward.
Proposition 4.21. Let MP be the I-MIP induced by P, . Then for all X⊆U, the following equations hold:
- (1)
,
- (2)
,
- (3)
.
Proof. (1) According to Proposition 4.13, rP(X) = |Y| where Y⊆X and for all T ∈ P, |Y∩T | ≤ 1. Let T ∈ P. If |Y∩T | = 0, then T∩X = ∅ and for all t ∈ T, rP(X) = rP(X ∪ {t}) − 1, that is, and for all t ∈ T, t ∉ {x ∈ U : rP(X) = rP(X ∪ {x})}; else, if |Y∩T | = 1, then X∩T ≠ ∅ and for all x ∈ T, rP(X) = rP(X ∪ {x}), that is, and for all t ∈ T, t ∈ {x ∈ U : rP(X) = rP(X ∪ {x})}. That is, .
Similarly, we can prove that (2) and (3) are true.
Proposition 4.21 provides three ways to get the upper approximation of X with rank function. This intensifies our understanding to rank function of MP.
Proposition 4.22. Let MP be the I-MIP induced by P, . Then for all X⊆U,
Proof. According to Proposition 4.14 and Corollary 4.15, we can get that cl P(X) = ∪{T ∈ P : x ∈ X ∧ x ∈ T}. Therefore, according to the definition of the upper approximation, it is obvious that .
The compact formulation of the upper approximation in Proposition 4.22 indicates that the closure is an efficient way to get the approximations in rough sets.
Proposition 4.23. Let MP be the I-MIP induced by P, ℋ(MP) = ℋP. Then for all X⊆U,
5. Matroidal Structure of Rough Sets Constructed from the Viewpoint of Cycle
In Section 3.2, the relationships between a cycle and an equivalence class are analyzed in detail. And a partition over the universe is transformed to a graph composed of some cycles. So, inspired by the cycle matroid introduced in [39], we will construct the matroidal structure of rough sets from this viewpoint. A new matroid will be established and the characteristics of it are studied. Then the approximations in rough sets are investigated via these characteristics.
For convenience, in this section, we suppose that U is a universe, R an equivalence relation over U, and P = U/R the partition. And is the graph induced by P, where .
5.1. The Second Type of Matroidal Structure of Rough Sets
In this subsection, the second type of matroid induced by a partition is defined. Similar to the discussion of I-MIP, the base, circuit, rank function, and closure of the second type of matroid are investigated.
From the analysis in Section 3.2, we know that for all T ∈ P and for all K ⊂ T, CK is not a cycle. Obviously, any subgraph of CK is also not a cycle. Therefore, we can get the following proposition.
Proposition 5.1. Let . Then there exists a matroid M′ on U such that .
Proof. According to Definition 2.3, we need to prove that satisfies (I1)~(I3). In terms of Section 3.2, for all T ∈ P, CT is the cycle whose vertices set is T, that is, CT = (T, ET) where ET is the set of edges of CT. So, it is obvious that satisfies (I1) and (I2). Here, we just need to prove satisfies (I3).
Let , |I1 | <|I2| and I2 − I1 = {e1, e2, …, em}(1 ≤ m≤|U|). Suppose that for all ei ∈ I2 − I1 for 1 ≤ i ≤ m, such that , that is, . Because , . It is obvious that . So . Since |I2 | = |I2 − I1 | +|I2∩I1|, we can get that |I1 | ≥|I2|. It is contradictory with the known conditions that |I1 | <|I2|. So ∃ei ∈ I2 − I1 such that for all T ∈ P, T ⊈ I1 ∪ {ei}, namely, . That is . As a result, satisfies (I1)~(I3). That is, there exists a matroid M′ on U such that .
The matroid mentioned in Proposition 5.1 is established from the viewpoint of cycle. It is a new type of matroid induced by a partition and is defined as follows.
Definition 5.2 (The second type of matroid induced by a partition). The second type of matroid induced by a partition P over U, denoted by II-MIP, is such a matroid whose ground set E = U and independent sets ℐ = {X⊆U : for all T ∈ P, CT ⊈ G[X]}.
Because of the intuition of a graph, it is easy to understand the matroid established in Definition 5.2. In fact, we can formulate a II-MIP as follows.
Proposition 5.3. Let where n = |P|. Then is a II-MIP.
Proof. Because Si ⊂ Ti, for all , X∩T ⊂ T for each T ∈ P. That means for all T ∈ P, , that is, . Conversely, for all , since for all T ∈ P, , we can get that T ⊈ X, that is, T∩X ⊂ T. So . As a result, is a II-MIP.
In terms of Propositions 5.1 and 5.3, we can find that the two matroids established in them are equivalent. That is to say for any matroid M = (U, ℐ), if , then M is a II-MIP. So, the following corollary can be obtained.
Corollary 5.4. .
Similar to the axiomatization of I-MIP, we will axiomatize II-MIP with the set of circuits of it in the following.
Theorem 5.5. Let M = (U, ℐ) be a matroid. Then M is a II-MIP if and only if for all C1, C2 ∈ 𝒞(M), C1∩C2 = ∅ and ∪𝒞(M) = U.
Proof. (⇒): Let M = (U, ℐ) be the II-MIP induced by P. Therefore, for all T ∈ P, T ∉ ℐ, and for all X ⊂ T, X ∈ ℐ. And then for all T ∈ P, T ∈ 𝒟(M). So, according to (2.2) and Definition 2.5, 𝒞(M) = P. Thus, for all C1, C2 ∈ 𝒞(M), C1∩C2 = ∅, and ∪𝒞(M) = U.
(⇐): Since for all C1, C2 ∈ 𝒞(M), C1∩C2 = ∅, and ∪𝒞(M) = U, we can regard the 𝒞(M) as a partition over U. Furthermore, 𝒟(M) = {X⊆U : ∃C ∈ 𝒞(M) s.t. C⊆X}. Because ℐ = 2U − 𝒟(M), for all X ∈ ℐ, ∄C ∈ 𝒞(M) such that C⊆X. According to Proposition 5.1 and Definition 5.2, we can get that . That is, M = (U, ℐ) is a II-MIP.
Theorem 4.5 shows there is one-to-one correspondence between a partition and the I-MIP induced by the partition. In the following theorem, we will discuss the relationship between a partition and the II-MIP induced by the partition.
Theorem 5.6. Let 𝒫 be the collection of all partitions over U, ℳ′ the set of all II-MIP induced by partitions of 𝒫, g : 𝒫 → ℳ′, that is, for all P ∈ 𝒫, where is the II-MIP induced by P. Then g satisfy the following conditions:
- (1)
for all P1, P2 ∈ 𝒫, if P1 ≠ P2 then g(P1) ≠ g(P2),
- (2)
for all s.t. .
Proof. (1) Let P1 and P2 are two different partitions over U, and , are two II-MIP induced by P1 and P2, respectively. We need to prove that there is an such that , or there is an such that . Because P1 ≠ P2, there must be an equivalence class T1 ∈ P1 such that T1 ∉ P2. Suppose that for all T ∈ P2, T1 ⊈ T. Then ∃X ⊂ T1 such that X ∈ {S : S ⊂ T1} and X ∉ {S : S ⊂ T, for all T ∈ P2}. According to Proposition 5.3, and . Conversely, if ∃T2 ∈ P2 such that T1⊆T2, then ∃X ⊂ T2 such that X ∈ {S : S ⊂ T2} and X ∉ {S : S ⊂ T, for all T ∈ P1}. Thus, according to Proposition 5.3, and .
(2) Let M′ = (U, ℐ′) be a II-MIP matroid. According to Theorem 5.5, 𝒞(M′) is a partition on U. That is, g(𝒞(M′)) = M′.
Theorem 5.6 shows that there is also a bijection between a partition and the II-MIP induced by the partition.
5.2. Characteristics of II-MIP
The II-MIP is established from the viewpoint of cycle. There is a big difference between the formulations of I-MIP and II-MIP and the same as the characteristics between them. In this subsection, we will formulate the characteristics of II-MIP.
A base of a matroid is one of the maximal independent sets of the matroid. From Propositions 5.1 and 5.3, the cardinality of one of the maximal independent sets is equal to |U | −|P| and just one element of each equivalence class does not belong to the independent set.
Proposition 5.7. Let be the II-MIP induced by P, n = |P|. Then is the set of bases of .
So any equivalence class is not contained in some base of a II-MIP. And there will be a cycle if a new element is put in the base. Specifically, if for all T ∈ P, |T | = 1, then . Next, we can also formulate the set of bases of a II-MIP from the viewpoint of graph as follows.
Corollary 5.8. does not contain a cycle}).
From Proposition 5.7 and Corollary 5.8, we can find that for all T ∈ P, if |T | = 1, then T is not contained in any base of the II-MIP induced by P. Therefore, we can get the following corollary.
Corollary 5.9. Let . Then .
As the analysis in Section 3.2, any equivalence class of a partition can be converted to a cycle. And any proper subset of an equivalence class does not form a cycle. So we can formulate the set of circuits of a II-MIP as follows.
Proposition 5.10. Let be the II-MIP induced by P. Then is the set of circuits of .
Proof. According to Theorem 5.5, it is straightforward.
Likewise, from the viewpoint of graph, we can get another formulation of the set of circuits of a II-MIP.
Corollary 5.11. is a cycle}.
Proof. According to the definition of and Proposition 5.10, it is straightforward.
Next, we will formulate the rank function of II-MIP.
Proposition 5.12. Let be the II-MIP induced by P. Then for all X⊆U, is the rank of X in .
In all the characteristics of a matroid introduced in this paper, the rank function of a matroid is the one and only one numeric characteristic. In the following content, we will further study some properties of the rank function of II-MIP.
Theorem 5.13. Let be the II-MIP induced by P, , and X⊆U an R-definable set. For all Y⊆U, if X∩Y = ∅, then .
Proof. Because X is an R-definable set and X∩Y = ∅, according to Proposition 5.3 and Corollary 5.4, for all I1∈ Max and for all I2∈ Max, I1∩I2 = ∅. Furthermore, and I1 ∪ I2 ∈ Max ({Z⊆X ∪ Y : for all T ∈ P, T ⊈ Z}). According to Definition 2.8, and . Because I1∩I2 = ∅, |I1 ∪ I2 | = |I1 | + I2. As a result, .
Theorem 5.13 provides a way to separate the rank of a subset into the sum of ranks of two disjoint sets contained in the subset. And one of the two disjoint sets is a definable set. It is obvious that any subset of the universe can be represented as the union of a definable set, and an indefinable set which are disjoint and contained in the subset. This will be very helpful to some proofs in the following. In order to study the properties of the rank function of II-MIP conveniently, the concept of lower approximation number will be defined as follows.
Definition 5.14 (Lower approximation number). Let R be a relation on U. For all X⊆U, f*R(X) = |{RNR(x) : x ∈ U∧RNR(x)⊆X}| is called the lower approximation number of X with respect to R. When there is no confusion, we omit the subscript R.
In classical rough sets, R usually refers to the equivalence relation. For a better understanding to the lower approximation number, an example is served.
Example 5.15. Let U = {a, b, c, d, e, f, g, h} be the universe, R an equivalence relation over U, and U/R = {T1, T2, T3, T4} = {{a, b}, {c}, {d, e, f}, {g, h}}. Compute the lower approximation numbers of X1, X2, and X3 where X1 = {a, b, c}, X2 = {a, d, g}, and X3 = {a, c, g, h}.
Because R is an equivalence relation, according to Definition 2.1, for all x ∈ U, RNR(x) = [x] R. Therefore, we can get that f*(X1) = |{T1, T2}| = 2, f*(X2) = |∅ | = 0, and f*(X3) = |{T2, T4}| = 2.
Similarly, according to Definition 2.2, we can get that f*(X1) = |{T1, T2}| = 2, f*(X2) = |{T1, T3, T4}| = 3, and f*(X3) = |{T1, T2, T4}| = 3.
Theorem 5.16. Let be the II-MIP induced by P, . Then for all X⊆U, .
Proof. Let A⊆X be the largest R-definable set contained in X. Then X = A ∪ (X − A). Thus X − A is an R-indefinable set and for all T ∈ P, T ⊈ X − A. According to Proposition 5.12 and Definition 5.14, and . Therefore, in terms of Theorem 5.13, .
Theorem 5.16 combines the lower approximation number and the rank function of II-MIP closely. And the formulation is very simple. This is useful to study rough sets with matroidal approaches and vice verse.
Lemma 5.17. Let be the II-MIP induced by P, . Then for all X⊆U, .
Proof. Let A⊆X be the largest R-definable set contained in X and B⊆ ~ X the largest R-definable set contained in ~X. Then, in terms of Theorem 5.16, and . So .
The last lemma discusses the relationship between the II-MIP ranks of a subset and its complementary set. For a subset X of U, if X is a definable set then ~X is also a definable set. So, we can get the following lemma.
Lemma 5.18. Let be the II-MIP induced by P, . Then for all X⊆U, X is an R-definable set if and only if .
Proof. (⇒): According to Theorems 5.13 and 5.16 and Lemma 5.17, it is straightforward.
(⇐): According to Lemma 5.17, |P | = f*(X) + f*(~X). Then, according to Definition 5.14, X is an R-definable set.
From Definition 2.9, we know that, for any subset X of U, if x ∈ U − X such that the rank of X ∪ {x} is equal to the rank of X, then x belongs to the closure of X. In II-MIP, we can say that if X ∪ {x} contains one cycle more than X, then x belongs to the closure of X.
Proposition 5.19. Let be the II-MIP induced by P. Then for all X⊆U, is the closure of X in .
Proof. According to Proposition 5.12, for all x ∈ X, . Then, in terms of Definition 2.9, . Let YX⊆X and . For all x ∈ U − X, if then . According to Proposition 5.12, for all T ∈ P, T ⊈ YX. That means ∃T ∈ P such that T⊆YX ∪ {x}, that is, ∃Y⊆YX such that Y ∪ {x} ∈ P. As a result .
The hyperplane of II-MIP can be formulated as follows.
Proposition 5.20. Let be the II-MIP induced by P. Then is the hyperplane of .
Proof. According to Definition 2.10, we need to prove that for all , H is a close set of , and . And more, we need to prove that for all Y⊆U, if , then Y is not a hyperplane of .
-
(1) Is a close set of .
-
For all , there is an equivalence class T ∈ P and a subset X⊆T such that |X | = 2 and H = U − X. Therefore, for all Y⊆H and for all x ∈ X, Y ∪ {x} is not an equivalence class, that is, Y ∪ {x} ∉ P. That is, the set {x ∈ X : ∃Y⊆H s.t. Y ∪ {x} ∈ P} = ∅. Thus, according to Proposition 5.19, . That is to say H is a close set of .
-
, .
-
For any T ∈ P, since T is R-definable, by Theorem 5.13
() -
That is,
() -
Furthermore, since ~T is also R-definable, by Theorem 5.13
() -
That is,
() -
(3) For all Y⊆U, if , then Y is not a hyperplane of .
-
If , then there are two cases.
-
(1) | U − Y | = 2 and U − Y ⊈ T, for all T ∈ P.
-
(2) | U − Y | ≠ 2.
-
Next, we discuss these two cases, respectively.
Case 1. By Proposition 5.19, so Y is not a close set.
Case 2. if |U − Y | = 1, then so Y is not a close set. If |U − Y | > 2, then suppose that . In that case, for T ∈ P such that (U − Y)∩T ≠ ∅, |(U − Y)∩T | ≥ 2. So
In that case, is not equal to .
Summing up, is the hyperplane of .
5.3. Approximations Established through II-MIP
In this subsection, we will redefine the lower and the upper approximations with some characteristics of II-MIP. Three pairs of approximations are established.
Proposition 5.10 shows that the set of circuits of a II-MIP is equal to the partition which induces the II-MIP. So we can get the following proposition.
Proposition 5.21. Let be the II-MIP induced by P, . Then for all X⊆U,
We know that the lower and the upper approximations of a subset are all definable sets. The lower approximation is the largest definable set contained in the subset. And the upper approximation is the smallest definable set, which contains the subset. Since Lemma 5.18 provides a way to decide whether a subset is a definable set, we can define the lower and the upper approximations as follows.
Proposition 5.22. Let be the II-MIP induced by P, . Then for all X⊆U,
Proof. According to Lemma 5.18, for all X⊆U, if , then X is an R-definable set. So is the largest R-definable set contained in X. And is the smallest R-definable set contained X. And then, according to (2.1), it is straightforward.
Next, we will establish the lower approximation via the closure of II-MIP.
Proposition 5.23. Let be the II-MIP induced by P, . Then for all X⊆U,
Proof. For all T ∈ P, if T⊆X, then for all x ∈ T, T − {x}⊆X. According to Proposition 5.19, . That is, . In terms of (2.1), .
In terms of (P2), we can get the upper approximation by using the duality. That is, .
6. Relationship between I-MIP and II-MIP
In the previous two sections, we have got two types of matroids induced by a partition from the viewpoints of complete graph and cycle, respectively. And it is can be found that the matroidal characteristics of them are very different. But, if the two types of matroid are induced by the same partition, what are the relationships between them? In this section, we will study this issue.
Definition 6.1 (Dual matroid see [39]). Let M = (E, ℐ) be a matroid, and ℬ the set of bases of M. The dual matroid M* is the matroid on the set E whose bases ℬ* = Com(ℬ). If ℐ(M) = ℐ(M*), then M is called an identically self-dual matroid.
For convenience, in the following content, we suppose that U is the universe, R is an equivalence relation over U, P = U/R is the partition on U, and MP is the I-MIP induced by P and the II-MIP induced by P.
Proposition 6.2. Let be the dual matroid of MP. Then .
Proof. For all B ∈ ℬ(MP), according to Definition 6.1, . For all T ∈ P such that |T∩B | = 1, ∃x ∈ T such that T − {x}⊆U − B. Therefore, where n = |P|. In terms of Proposition 5.7, . As a result, .
Proposition 6.2 shows that MP and are dual matroids. This result is very interesting and helpful to study rough sets. Maybe people want to ask some questions about the relationships between MP and as follows: whether a I-MIP and a II-MIP which induced by different partitions could be dual matroids? And whether two different I-MIP (or II-MIP) could be dual matroids? Next, we will answer them.
Proposition 6.3. Let P1 and P2 be two partitions over U, the I-MIP induced by P1, and the II-MIP induced by P2. Then if and only if P1 = P2.
Proposition 6.3 shows that a I-MIP and a II-MIP induced by different partitions are not dual matroids.
Proposition 6.4. Let P1 and P2 be two different partitions over U and and are the I-MIP induced by P1 and P2, respectively. Then .
Proof. Suppose that . From Proposition 6.2, is a II-MIP. In terms of Proposition 5.10, we can get that . Therefore, according to Theorem 4.4, for all T ∈ P1, |T | = 2. Thus P1 = P2. This is contrary to the known condition that P1 and P2 are two different partitions over U. As a result, .
Proposition 6.5. Let P1 and P2 be two different partitions over U and and are the II-MIP induced by P1 and P2, respectively. Then .
Proof. Similar to the proof of Proposition 6.4, it is straightforward.
Propositions 6.4 and 6.5 show that two different I-MIP are not dual matroids. And the same as two different II-MIP. One can find that we emphasize in Propositions 6.4 and 6.5 that P1 and P2 are two different partitions over U. So, in Propositions 6.4 and 6.5, could be equal to when P1 = P2? We will discuss this problem in the following proposition.
Proposition 6.6. if and only if for all T ∈ P, |T | = 2.
Proof. (⇒): According to Definition 6.1, if , then . According to Propositions 4.1, 4.3, and 5.1, for all T ∈ P, |T | = 2.
(⇐): It is straightforward.
Proposition 6.6 provides a necessary and sufficient condition to decide whether a I-MIP or a II-MIP is a self-dual matroid. This gives a good answer to the previous question that whether could be equal to when P1 = P2.
Next, we will study when a hyperplane of MP is also a hyperplane of .
Proposition 6.7. Let H ∈ ℋ(MP). Then if and only if U − H ∈ 𝒞(MP).
Proof. (⇒): According to Proposition 4.16, U − H ∈ P, that is, ∃T ∈ P such that U − H = T. If , according to Proposition 5.20, then |U − H | = |T | = 2. According to Proposition 4.10 and Corollary 4.11, T ∈ 𝒞(MP), that is, U − H ∈ 𝒞(MP).
(⇐): If U − H ∈ 𝒞(MP), then |U − H | = 2 and ∃T ∈ P such that T = U − H. Therefore, according to Propositions 4.16 and 5.20, .
From the Propositions 4.14 and 5.19, we can find, for any subset X⊆U, that the is generally the subset of cl P(X). Now, we will study under what conditions that the is certain the subset of cl P(X).
Proposition 6.8. Let X⊆U, , and . Then if and only if for all x ∈ U − X, .
Proof. (⇒): Let . According to Propositions 4.14 and 5.19, we can get that {y ∈ U − X : ∃Y⊆X s.t. Y ∪ {y} ∈ P}⊆{y ∈ U − X : x ∈ X∧xy ∈ EP}. That is, for all y ∈ {y ∈ U − X : ∃Y⊆X s.t. Y ∪ {y} ∈ P}, y ∈ {y ∈ U − X : x ∈ X∧xy ∈ EP}. In terms of Section 4, we know that EP = {xy : x ≠ y∧(∃T ∈ P s.t. {x, y}⊆T)}. Therefore, for all y ∈ {y ∈ U − X : x ∈ X ∧ xy ∈ EP}, {y} ∉ P. And for all y ∈ {y ∈ U − X : ∃Y⊆X s.t. Y ∪ {y} ∈ P}, {y} ∉ P. That is, for all x ∈ U − X, .
(⇐): According to Propositions 4.14 and 5.19, it is straightforward.
The formulation of rank functions of MP and are very different. In consideration of that MP and are dual matroids, it is meaningful to discuss the relationship between the rank functions of them.
Theorem 6.9. Let X⊆U, , and . Then if and only if |X | = f*(X) + f*(X).
Proof. (⇒): If , according to Theorem 5.16, rP(X) = |X | − f*(X). Then, in terms of Definition 2.2 and Proposition 4.13, we can get that rP(X) = f*(X). Therefore, f*(X) = |X | − f*(X). And then |X | = f*X + f*(X).
(⇐): With the same way used in the above proof, it is straightforward.
In Theorem 6.9, we make use of the lower and the upper approximations numbers to discuss the relationship between the rank functions of MP and . It adequately reflects the close relation between rough sets and matroids.
7. Conclusions
We make a further study to the combination of rough sets and matroids. Two graphical ways are provided to establish and understand the matroidal structure of rough sets intuitively. For a better research on the relationships between rough sets and matroids, the concept of lower approximation number is proposed. And then, some meaningful results are obtained. For example, Theorem 5.16 shows that, for any subset X⊆U, the rank of X within the context of II-MIP is equal to the difference of the cardinality and the lower approximation number of X. And Theorem 6.9 indicates that the rank of X within the context of I-MIP is equal to it within the context of II-MIP if and only if the cardinality of X is equal to the difference of its lower and upper approximation numbers. Furthermore, the relationships between the two kinds of matroids established in Sections 4 and 5 are discussed. It is so exciting that the two kinds of matroids are dual matroids. And this is meaningful to the study of the combination of rough sets and matroids.
Matroids possess a sophisticated mathematical structure. And it has been widely used in real world. So we hope our work in this paper could be contributive to the theoretical development and applications of rough sets. In future works, we will study the axiomatization of rough sets with matroidal approaches and explore the wider applications of rough sets with matroids.
Acknowledgments
This work is in part supported by National Science Foundation of China under Grant nos. 60873077, 61170128 and the Natural Science Foundation of Fujian Province, China under Grant no. 2011J01374.




