Robust Stability of Switched Delay Systems with Average Dwell Time under Asynchronous Switching
Abstract
The problem of robust stability of switched delay systems with average dwell time under asynchronous switching is investigated. By taking advantage of the average dwell-time method and an integral inequality, two sufficient conditions are developed to guarantee the global exponential stability of the considered switched system. Finally, a numerical example is provided to demonstrate the effectiveness and feasibility of the proposed techniques.
1. Introduction
In recent years, there has been increasing interest in the analysis and switched systems because of its applications in a variety of areas such as signal processing, signal estimation, pattern recognition, communications, control application, and many practical control systems. Switched linear systems comprise a collection of linear subsystems described by differential or difference equations and a switching law to specify the switching among these subsystems. A switched system is a combination of discrete and continuous dynamical systems. All of these systems arise as models for phenomena which cannot be described by exclusively continuous or exclusively discrete processes. Most recently, on the basis of Lyapunov functions and other analysis tools, the stability or stabilization for linear or nonlinear switched systems has been further investigated, and many valuable results have been obtained, for a recent survey on this topic and related questions has attracted increasing attention [1–10]. The average dwell-time is an effective method for the switched systems which do not exist common Lyapunov function. Time delay commonly exists in engineering. Because of time delay, the system can become unstable or less capable, it is significant to study time delay. There are two kinds of stability for switched systems with time delay: time delay-independent stability and time delay-dependent stability. The time delay-independent stability is obviously conservative to the bounded time delay or small time delay, many results are obtained [11–13]. At present, there has been increasing interest in time-delay switched systems, and many valuable results have been obtained [14–18].
It is worth noting that the aforementioned results are all based on the basic assumption that the switching instants are simultaneous with those of the system. However, in actual operation, there inevitably exists asynchronous switching between the controllers and the practical subsystems, that is to say, the real switching instants of the controller exceed or lag behind those of the system, which will deteriorate performance of the systems. In fact, the necessity of taking into consideration the asynchronous switching is shown in efficient controller design in many mechanical and chemical systems. There are some results presented on control synthesis under asynchronous switching which have been proposed [19–28]. However, to the best of our knowledge, the issue of switched delay systems under asynchronous switching has not fully been investigated, which motivated this study for us.
In this paper, we deal with the problem of robust stability and L2-gain of switched delay systems under asynchronous switching. In terms of the average dwell-time method and an integral inequality, two sufficient conditions are developed to guarantee the global exponential stability of the considered switched system. Finally, a numerical example is provided to illustrate the effectiveness and feasibility.
Notations. Throughout this paper, ℜn denotes the n-dimensional Euclidean space and ℜn×n refers to the set of all n × m real matrices. For real symmetric matrices X and Y, the notation X ≥ Y (resp., X > Y) mean that the matrix X, Y are positive semidefinite, (resp., and positive definite). I is the identity matrix with appropriate dimensions. * represents the elements below the main diagonal of a symmetric matrix. The superscripts ⊺ and −1 stand for matrix transposition and matrix inverse, respectively; ∥·∥c denotes the Euclidean norm. λmax (P) and λmin (P) denote the maximum and minimum eigenvalues of matrix P, respectively. The shorthand diag {M1, …, Mn} denotes a block diagonal matrix with diagonal blocks being the matrices M1, …, Mn. In this paper, if not explicit, matrices are assumed to have compatible dimensions.
2. Preliminaries
First of all, we will give some definitions and lemmas about system (2.6) which plays an important role in the derivation of our result.
Definition 2.1 (see [29].)The unforced system is said to be exponential stable if there exist constants ν > 0 and ϑ > 0 such that
Definition 2.2 (see [30].)For γ > 0, the switched system (2.1) is said to have weighted L2-gain, if under zero initial condition ϕ(t), t ∈ [−τM, 0], it holds that
Definition 2.3 (see [30].)For any T2 > T1 ≥ 0, let Nσ(T1, T2) denote the switching number of discontinuities of σ(t) during on an intercal (T1, T2). If Nσ(T1, T2) ≤ N0 + (T2 − T1)/Ta holds for N0 ≥ 0 and Ta > 0, then N0 and Ta are called chattering bound and average dwell time, respectively. Here we assume N0 = 0 for simplicity as commonly used in the literature.
Lemma 2.4 (see [29].)For any given symmetric positive definite matrix X ∈ ℜn×n, and scalars α > 0, 0 ≤ d1 < d2, if there exists a vector function such that the following integration is well defined, then
Lemma 2.5 (see [28].)Let ϱ ≥ 0 and θ > δ > 0. If there exists a real-value continuous function x(t) ≥ 0, t ≥ t0, such that the differential inequality
Lemma 2.6 (see [9].)If a real scalar function x(t) satisfies the following differential inequality:
3. Main Results
Theorem 3.1. For given scalars 0 ≤ τ0 ≤ τM, α > 0, β > 0, then the system (2.1) is exponentially stable, if there exist positive-definite matrices Pi, Pij, Qki, Qkij (k = 1,2, 3), and Rli, Rlij (l = 1,2) such that the following LMIs hold:
In this case, for any switching signal with the average dwell-time satisfying
Proof. When t ∈ Λ1, we consider the following Lyapunov-Krasovskii functional:
Taking the time derivative of Vi(t, x(t)) for t ∈ [0, ∞) along the trajectory of the system (2.1) turns out to be
On the other hand, according to Lemma 2.4, we get that
Then we can get
In view of Schur complement, (3.3) implies that . Then we have for all ψ(t) ≠ 0.
Then during the matched period, by Lemma 2.5, Vi(t, x(t)) satisfy
When t ∈ Λ2, we consider the following Lyapunov-Krasovskii functional:
Similarly we have that
Through Lemma 2.5, we also have
When t ∈ [tℑ, tℑ + Δℑ), ℑ = 1,2, …, we have the relationship , and it follows that
From (3.7), we can obtain
Then through (3.23) and (3.24), we can easily get
By (3.9) and (3.25), then we have
Similarly, when t ∈ Λ1, we can also have
For convenience, let a = max {a1, a2}, b = min i≠j,i,j∈ℙλmin (Pi, Pij), through (3.27) and (3.29), we have
Theorem 3.2. For given scalars 0 ≤ τ0 ≤ τM, α > 0, β > 0, then the system (2.1) is exponentially stable with L2-gain, if there exist positive-definite matrices Pi, Pij, Qki, Qkij (k = 1,2, 3), and Rli, Rlij (l = 1,2) such that the following LMIs hold:
Proof. For all nonzero ω(t) ∈ L2[0, ∞) and a scalar γ > 0, then we establish system (2.1) with L2-gain performance . For convenience, denoting .
When t ∈ [t0, t1)∪[tℑ−1 + Δℑ−1, tℑ), k = 2,3, …, by the system (2.1), we can obtain
From (3.32), we can easily get
Integrate this inequality during [t0, t], it is known that
When t ∈ [tℑ, tℑ + Δℑ), ℑ = 2,3, …, by the system (2.1), by the same way, we can obtain
Then we have
When t ∈ [tℑ, tℑ + Δℑ), ℑ = 1,2, …, it follows that
Under the zero initial condition, Let t0 = 0, (3.40) implies
Integrate (3.41) during [0, ∞), then we can obtain
When t ∈ [t0, t1)∪[tℑ−1 + Δℑ−1, tℑ), ℑ = 2,3, …, by the same mathematical operations, we have .
From which we can get . This proof is completed.
Remark 3.3. If μ1 = μ2 = 0, which implies that Pi = Pij = P, Qki = Qkij = Qk, Rli = Rlij = Rl, i, j ∈ ℙ, by (3.3)-(3.4) and (3.32)-(3.33), we have Ta = 0, then it requires a common Lyapunov functional for all subsystems, and the switching signals can be arbitrary. If μk → ∞ (k = 1,2), we get from (3.3)-(3.4) and (3.32)-(3.33) that there is no switching, that is, switching signal will have a great dwell-time on the average.
4. Illustrative Example
In this section, a numerical example is given to illustrate the effectiveness of the obtained results.
Example 4.1. Consider the system (2.1) with parameters as follows:
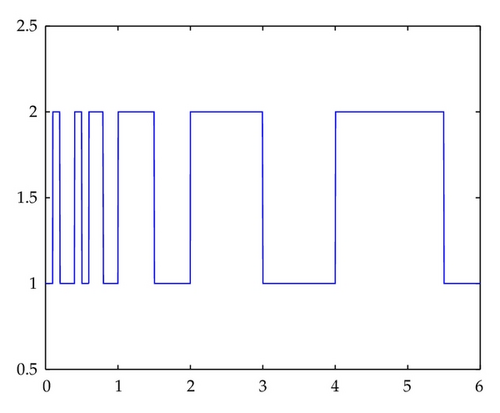
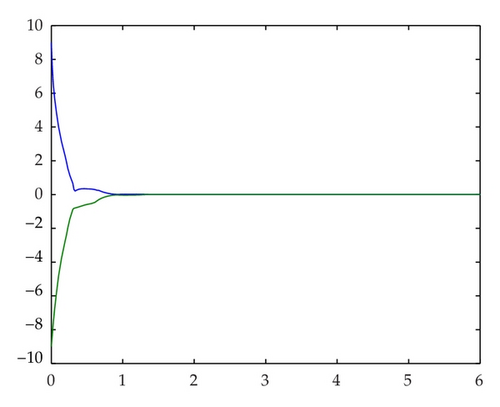
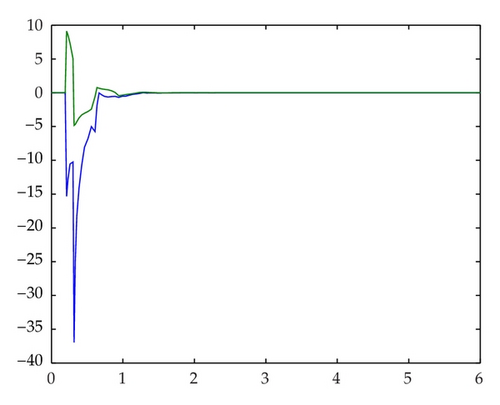
τ0 is fixed and assumed to be 0.2. The initial condition is assumed to be x(0) = [9, − 9] ⊺, ω(t) = 0.5sin t. Then by solving the LMIs in Theorem 3.2, different Ta and τM for different μ1μ2, α, and β can be obtained in Table 1. It can be seen that, for the given τ0, the upper bounds of the time delay τM and the minimal average dwell-time Ta are dependent on α, β, and μ1μ2. Then the simulation result of the system is shown in Figures 1, 2, and 3. The switching signal σ(t) with average dwell-time Ta is shown in Figure 1. Figures 2–3 indicate that the state response of the switched system without asynchronous switching and with asynchronous switching, respectively.
| μ1μ2 | 1.0 | 1.5 | 2.0 |
|---|---|---|---|
| Ta | 0.0521 | 2.1022 | 5.2454 |
| τM | 1.2036 | 1.5415 | 1.7154 |
5. Conclusions
In terms of the LMI approach, the problem of robust stabilization of switched delay systems with average dwell-time under asynchronous switching has been considered. Two sufficient conditions are developed to guarantee the global exponential stability of the considered switched system. At last, a numerical example is provided to demonstrate the effectiveness and feasibility of the proposed techniques.
Acknowledgment
This work was supported by the Fundamental Research Funds for the Central Universities (103.1.2E022050205).




