Volume 2012, Issue 1 950590

Research Article

Open Access

Exponential Passification of Markovian Jump Nonlinear Systems with Partially Known Transition Rates

Corresponding Author

Mengzhuo Luo

[email protected]

School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China uestc.edu.cn

Search for more papers by this author

Shouming Zhong,

Shouming Zhong

School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China uestc.edu.cn

Key Laboratory for Neuroinformation of Ministry of Education, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China uestc.edu.cn

Search for more papers by this author

Mengzhuo Luo,

Corresponding Author

Mengzhuo Luo

[email protected]

School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China uestc.edu.cn

Search for more papers by this author

Shouming Zhong,

Shouming Zhong

School of Mathematical Sciences, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China uestc.edu.cn

Key Laboratory for Neuroinformation of Ministry of Education, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China uestc.edu.cn

Search for more papers by this author

First published: 14 March 2012

https://doi.org/10.1155/2012/950590

Academic Editor: Ying U. Hu

Share a link

Email
Wechat
Bluesky

Abstract

The problems of delay-dependent exponential passivity analysis and exponential passification of uncertain Markovian jump systems (MJSs) with partially known transition rates are investigated. In the deterministic model, the time-varying delay is in a given range and the uncertainties are assumed to be norm bounded. With constructing appropriate Lyapunov-Krasovskii functional (LKF) combining with Jensen’s inequality and the free-weighting matrix method, delay-dependent exponential passification conditions are obtained in terms of linear matrix inequalities (LMI). Based on the condition, desired state-feedback controllers are designed, which guarantee that the closed-loop MJS is exponentially passive. Finally, a numerical example is given to illustrate the effectiveness of the proposed approach.

1. Introduction

In recent years, more and more attention has been devoted to the Markovian jump systems since they are introduced by Krasovskii and Lidskii [1]. It is known that systems with Markovian jump parameters are a set of systems with transition among the models governed by a Markov chain taking values in a finite set. They have the character of stochastic hybrid systems with two components in the state. The first one refers to the mode which is described by a continuous-time finite-state Markov process, and the second one refers to the state which is represented by a system of differential equations. Markovian jump systems have got the virtue of modeling the abrupt phenomena such as random failures and repairs of the components changes in the interconnections of subsystems, sudden environment changes, and so forth, which often takes place in many dynamical systems [2–4]. So due to extensive applications of such systems in manufacturing systems, power systems, communication systems, and network-based control systems, recently, many works have been reported about MJSs, which including filtering problems [5–7], stability analysis problems [8–12], and control problems [13–20], and so forth.

However, the aforementioned references almost considered that the transition probabilities are known exactly. In some practical applications, the mode information is transmitted through unreliable networks, it may be lost or observed simultaneously. That means the systems mode is neither totally accessible or inaccessible. So the ideal assumption on the transition probabilities inevitably limits the application of the traditional Markovian jump systems theory. Therefore, whether in theory or in practice, it is necessary to further consider more general systems with partially mode information [21–27].

Recently, the passivity problems for a variety of practical systems have been attracting renewing attention [28–31]. The passivity theory was first proposed in the circuit analysis [32] so it has played an efficient role in both electrical network and nonlinear control systems. The main point of passivity theory is that the passive properties of system can keep the system internal stability. Thus, the passivity theory provides a nice tool for analyzing the stability of a nonlinear system, and the passivity analysis has received a lot of attention and has found applications in diverse areas such as signal processing, complexity, chaos control and synchronization, and fuzzy control [33–38]. In [33] authors dealt with global robust passivity analysis for stochastic interval neural networks with interval time varying delays and Markovian jumping parameter; in [34] both delay-independent and delay-dependent stochastic passivity conditions are presented for uncertain neural networks; in [35–37] authors discussed the robust passivity and passification of Markovian jump systems and fuzzy time-delay systems; in [38], the exponential passivity of neural networks with time-varying are studied and the results are extended to two types of uncertainties.

In practice, input delays are often encountered in control systems because of the transmission of measurement information. Especially, in networked control systems, sensors controllers, and plants are often connected by a net medium hence it is quite meaningful to study the effect of the input delay in the design of controllers. However, to the best of the authors’ knowledge providing less conservative delay-dependent exponential passification criteria for uncertain MJS with input delays and partially known transition rates to desired performance are still open problems.

Motivated by this observation, in this paper, we study the exponential passification problem of nonlinear Markovian jump systems with partially known transition rates, including state and input delays, the aim of this problem is to design a controller such that the resulting closed-loop systems satisfy a certain passivity performance index. Comparing with the large amount of the literature on the analysis of stability of Markovian jump systems, passivity analysis and passification for these systems have many obvious advantages. Thus, research in this area should be of both theoretical and practical importance, which motivates us to carry out the present work. Based on the LKF theory and the free-weighting matrix method, some desired exponentially passification controllers are designed, which guarantee that the closed-loop MJS is exponential passive. Finally, a numerical example is used to illustrate the designed method.

Notations.

The notations are quite standard. Throughout this letter ℝⁿ and ℝ^n×m denote, resp., the n-dimensioned Euclidean space and the set of all n × m real matrices. The notation X ≥ Y (resp., X > Y) means that X and Y are symmetric matrices, and that X − Y is positive semidefinitive (resp., positive definite). ∥·∥ is the Euclidean norm in ℝⁿ. I is the identity matrix with compatible dimension. If A is a matrix, λ_max (A) (respective λ_min (A)) means the largest (respective smallest) eigervalue of A. Moreover, let be a complete probability space with a filteration. satisfies the usual conditions (i.e, the filtration contains all P-null sets and is right continuous). E{·} stands for the mathematical expectation operator with respect to the given probability measure. Denote by the family of all 𝔽₀ measurable -valued random variables such that . The asterisk * in a matrix is used to denote term that is induced by symmetry. Matrices, if not explicitly specified, are assumed to have appropriate dimensions. Sometimes, the arguments of function will be omitted in the analysis when no confusion can be arised.

2. Problem Formulation and Preliminaries

Consider the following uncertain MJS with time-varying delays

(2.1)

(2.2)

Here x(t) ∈ ℝⁿ is the state vector, u(t) ∈ ℝ^p is the control input, z(t) ∈ ℝ^q is the control output, and ω(t) ∈ ℝ^l is the exogenous disturbance input which belongs to 𝕃₂ [0, ∞], {r_t, t ≥ 0} is a homogenous finite-state Markov process with right continuous trajectories, which takes value in a finite-state space S = {1,2, …, N} with generator Π = {π_ij}, i, j ∈ S and has the mode transition probabilities

(2.3)

where Δt > 0, lim _Δt→0 (o(Δt)/Δt) = 0, π_ij is the transition rete from i to j, and

(2.4)

For notational simplicity, which r_t = i, i ∈ S, the matrices A(t, r_t), A_d(t, r_t), B₁(t, r_t), E₁(t, r_t), C(t, r_t), C_d(t, r_t), B₂(t, r_t), E₂(t, r_t), D₀(r_t), D₁(r_t), and D₂(r_t) will be described by A_i(t), A_di(t), B_1i(t), E_1i(t), C_i(t), C_di(t), B_2i(t), E_2i(t), D_0i, D_1i, and D_2i. We denote that

(2.5)

where A_i, A_di, B_1i, E_1i, C_i, C_di, B_2i, E_2i, and D_0i, D_1i, D_2i are known constant matrices with appropriate dimensions. In this paper, the transition rates of Markov chain are partially known, that is, some elements in matrix Π are unknown. We denote that

(2.6)

moreover, if

, it is further described as

Remark 2.1. represents the index of the lth known element in the ith row of transition rate matrix. The case m = N − 1 is excluded, which means if we have only one unknown element, one can naturally calculate it from the known elements in each row and the transition rate matrix property.

Now the mode-dependent state-feedback controller is taken to be as follows:

(2.7)

then, the closed-loop MJS can be represented as

(2.8)

Before proceeding further, we will introduce the following assumptions, definition and some lemmas which will be used in the next section.

Assumption 1. The uncertain parameters are assumed to be of the form:

(2.9)

where T_1i, T_2i, and N_ki, k = 1,2, 3,4, i ∈ S are known real constant matrices with appropriate dimensions and F_i(t), for all i ∈ S, are unknown time-varying matrix functions satisfying

(2.10)

Remark 2.2. It is assumed that all the elements F_i(t), for all i ∈ S, are Lebesgue measurable. The matrices ΔA_i(t), ΔA_di(t), ΔB_1i(t), ΔE_1i(t), ΔC_i(t), ΔC_di(t), ΔB_2i(t), and ΔE_2i(t) are said to be admissible if and only if both (2.9) and (2.10) hold. The parameter uncertainty structure as in Assumption 1 is an extension of the so-called matching condition, which has been widely used in the problems of control and robust filtering of uncertain linear systems.

Assumption 2. The time-varying delay τ_i(t) satisfies , with τ_1i, τ_2i, and μ_i being real constant scalars for each for all i ∈ S.

Assumption 3. For a fixed system mode r_t = i ∈ S, there exists a know real constant mode-dependent matrix Γ_i = diag (k_1i, k_2i, …, k_ni) > 0 such that the nonlinear vector function f(·, ·) satisfy the following conditions:

(2.11)

Definition 2.3 (see [39].)The MJS (2.8) is said to be passive if there exists a constant δ such that

(2.12)

holds for all T ≥ 0.

Definition 2.4. The MJS (2.8) is said to be exponentially passive from input ω(t) to output z(t), if there exists an exponential Lyapunov function (or called the exponential storage funtion) V defined on ℝⁿ, and positive scalars ρ, γ such that for all ω(t), all initial conditions x(0), all t ≥ 0, the following inequality holds:

(2.13)

Remark 2.5. From Definition 2.4, if ρ = 0, then the MJS in the form (2.8) is passive, in other words, exponential passivity implies passivity. It follows from (2.13) that

(2.14)

Then from Definition 2.3, we can see that MJS (2.8) is passive. But the converse does not necessarily hold, that is, we can not obtain the exponential passive if systems are passive.

Lemma 2.6 (see [36].)Let Q(x) = Q^T(x), R(x) = R^T(x), and S(x) depend affinely on x. Then the following linear matrix inequality:

(2.15)

holds if and only if one of the following conditions holds:

(1)
R(x) > 0, Q(x) − S(x)R⁻¹(x)S^T(x) > 0;
(2)
Q(x) > 0, R(x) − S^T(x)Q⁻¹(x)S(x) > 0.

Lemma 2.7 (see [40].)Let A, D, S, F, and P be real matrices of appropriate dimensions with P > 0 and F satisfy F^T(t)F(t) ≤ I. Then the following statement holds.

(1)
For any scalar ε > 0

(2.16)

(2)
For any vectors x and y with appropriate dimensions

(2.17)

Lemma 2.8 (see [41].)Let A, X be real matrices with appropriate dimensions. Then there exist a matrix P = P^T > 0 such that PA^T + AP + X < 0, if and only if, there exists a scalar ε > 0 and Z such that

(2.18)

3. Main Results

3.1. Exponential Passivity Analysis

In this section, we assumed the transition rates are partially known and given the state-feedback controller gain matrix K_i, i ∈ S, at first, we will present a sufficient condition, which guarantees the MLS (2.8) is exponential passive.

Theorem 3.1. Given the state-feedback controller gain matrix K_i, the uncertain MJS (2.8) is exponentially passive in the sense of expectation if there exists positive definite matrices , positive scalars γ, ε_1i, ε_2i, and for any matrices G_i, M_i, R_i, U_i, V_i, H_i with appropriate dimensions such that the following matrices inequalities hold for all i = 1,2, …, N:

(3.1)

Case 1. If

(3.2)

(3.3)

(3.4)

Case 2. If

(3.5)

(3.6)

(3.7)

(3.8)

(3.9)

where

(3.10)

Proof. First, in order to cast our model involved in the framework of the Markov process, we define a new process , and let L be the weak infinitesimal generator of the random process x_t(s), t ≥ 0 and

(3.11)

Now consider the Lyapunov-Krasovskii functional as follows for r_t = i, i ∈ 1,2, …, S:

(3.12)

where

(3.13)

where

(3.14)

In order to show the exponential passivity of the MJS (2.8) under the given controller gain matrix K_i, we set

(3.15)

Notice that

(3.16)

Then using Newton-Leibniz formula, for any matrices H_i, G_i, M_i, R_i, U_i, V_i we have

(3.17)

where

(3.18)

From the Lemma 2.7 (2.2), it is easy to see that

(3.19)

Now by Assumption 3, it can be deduced that for any positive scalar ε_1i, i ∈ 1,2, …, S,

(3.20)

Then from the above discussion, we can see that

(3.21)

where

(3.22)

other terms of Ω_i,i×j(t) are similar to

. In order to get our results, we will describe that the Φ₁(t) < 0 and Φ₂(t) < 0. By the Schur complement, Φ₁(t) < 0 and Φ₂(t) < 0 under the restriction of (3.14) if and only if

(3.23)

where Ω_{i,9 × 9} is the nominal matrix of Ω_{i,9 × 9}(t). Then from the Lemma 2.7 (2.1), above matrix inequality holds, which is equivalent to

(3.24)

Case 1. If

then (3.24) is equivalent to

(3.25)

Obviously, we can see that if (3.1) and (3.4) hold, then Φ₁(t) < 0 and Φ₂(t) < 0 under the restriction of (3.14). Next we will further consider the equivalent form of (3.14).

is equivalent to

(3.26)

If we have the following matrix inequalities hold, we can have that (3.14) is satisfied

(3.27)

Obviously, (3.27) is equivalent to (3.2) and (3.3) by the Schur complement.

Case 2. If

then (3.24) is equivalent to

(3.28)

Then if (3.1), (3.8), and (3.9) hold, then Φ₁(t) < 0 and Φ₂(t) < 0 under the restriction of (3.14), furthermore, with the similar consideration, we can deduce that if (3.5)–(3.7) are established, then (3.14) is founded. So there exists a positive scalar ρ₁, then

(3.29)

On the other hand, it is easy to obtain that

(3.30)

where ∥P∥ = max _i∈S {∥P_i∥}, ∥Q∥ = max _i∈S {∥Q_i∥}.Let ρ > 0 be sufficiently small such that

(3.31)

So, by Definition 2.4, the MJS (2.8) is exponentially passive. This completes the proof.

Remark 3.2. It is easy to derive that the MJS (2.8) is exponential mean square stability with ω(t) = 0 if the MJS (2.8) is exponentially passive. Moreover, the result of Theorem 3.1 makes use of the information of the subsystems upper bounds of the time varying delays, which may bring us less conservativeness, and from the free-weighting matrix and Newton-Leibnitz formula, the upper bounds of μ_i are not restricted to be less than 1 in this paper. Therefore, our result is more natural and reasonable to the Markovian jump systems.

Remark 3.3. In order to obtain the gain matrices K_i for convenience in the next section, (3.1) is not LMI, if we substitute ε_2i by and use the Lemma 2.7 (2.1), we can obtain the equivalent form of LMI.

3.2. Exponential Passification

In this section, we will determine the feedback controller gain matrices K_i, i ∈ S in (2.7), which guarantee that the closed-loop MJS (2.8) is exponentially passive with partially known transition rates.

Theorem 3.4. Given a positive constant ε, there exists a state-feedback controller in the form (2.7) such that the closed-loop MJS (2.8) is exponentially passive if there exist positive definite matrices , positive scalar ε_1i, ε_2i, and for any matrices with appropriate dimensions satisfying the following LMIs under the two cases for all i = 1,2, …, N.

Case 1. If

(3.32)

(3.33)

(3.34)

(3.35)

Case 2. If

(3.36)

(3.37)

(3.38)

(3.39)

(3.40)

(3.41)

where

(3.42)

when the LMIs are feasible, a desired state-feedback controller can be obtained in the form of (2.7) with the controller gains given by K_i = Y_iP_i for all i ∈ S.

Proof. At first, we list the following fact:

(3.43)

which implies that

(3.44)

Now perform a congruence transformation to (3.1) by

(3.45)

If , then by the Schur complement and (3.44), we can infer that (3.34) is established. In the same way, if , (3.39) is established.

From Lemma 2.8, we can see that (3.35) is equivalent to , so (3.4) can be established. Furthermore, using the same method that proposed above, we can deduced that (3.32), (3.33), (3.36)–(3.38), and (3.40) are equivalent to (3.2) (3.3), (3.5)–(3.7), and (3.8), respectively. In conclusion, the gain matrix of desired controller in the form of (2.7) is given by K_i = Y_iP_i. This completes the proof.

Remark 3.5. To reduce the conservatism, when estimating is not simply enlarged as , but , are considered as well, and different free-weighting matrices are introduced. This method above may lead to obtain improved feasible region for delay-dependent exponential passivity criteria.

Remark 3.6. In fact, Theorem 3.1 gives a exponential passivity criteria for MJS (2.8) with , where μ_i is a given constant. In many cases, μ_i is unknown. Considering this case, a rate-independent criteria for a delay satisfying τ_1i ≤ τ_i(t) ≤ τ_2i is derived as follows by setting Q_i = Q^* = 0, for all i ∈ S in the proof of Theorem 3.1.

4. Examples

In this section, we will consider a interval time-varying delay MJS in the form of (2.8) with three modes, and the parameters of the system are given as follows:

(4.1)

The two cases of the transition rates matrices are described as follows:

(4.2)

where ? means the unknown element. With the choice of ε = 0.2 and

, we can obtain the feasibility solution of case 1 and case 2 as follows. Case 1:

(4.3)

case 2:

(4.4)

Under the two cases above, Table 1 lists the state-feedback controller gains matrix K_i, which can be determined by the method of Theorem 3.4. If the ρ is sufficiently small, we can check that the MJS (2.8) is exponentially passive under the condition of Theorem 3.4. Given the initial condition as x(t) = (2.0 −2.0)^T and r(t) = 2, from Figures 1 and 2, we can easily see that the closed-loop system in (2.8) is mean square exponential stable with ω(t) = 0.

Table 1. Calculated the controller gains matrix for different cases.

	Case 1	Case 2
K₁	(−0.2256, 0.0218)	(−2.4527, 0.2749)
K₂	(−0.4330, − 0.1248)	(−0.4842, 0.1157)
K₃	(−0.2800, − 0.1641)	(−1.0109, − 0.1008)

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

State response of case 1 and the switch signal.

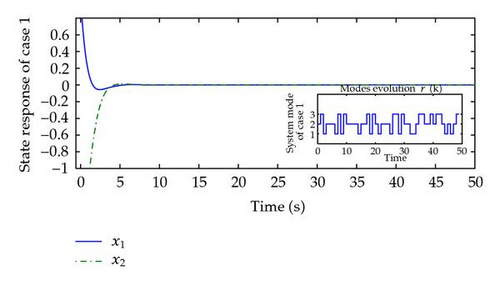
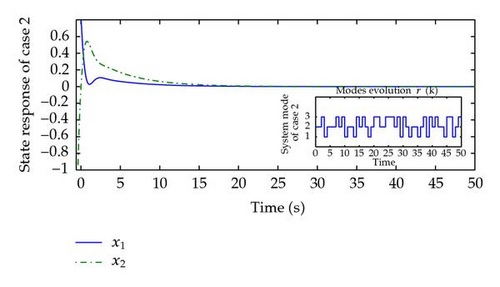
Remark 4.1. In order to illustrate the effectiveness of the proposed approach, a numerical example is given which included two cases, that is, case 1, the transition rate matrix is completely known; case 2, some elements in the transition rate matrix are inaccessible. By using Matlab Toolbox, we can obtain the gain matrix K_i, which guarantees that the Markovian jump systems (2.8) is robust exponential passivity. If we choose the switch signal as Figures 1 and 2, we can know that the closed-loop system (2.8) is exponentially stable in the mean square under the state-feedback controllers obtained above, which have been listed in Table 1.

5. Conclusions

In this paper, the problems of exponential passification of uncertain MJS have been investigated. To reflect more realistic dynamical behaviors of the system, both the partially known transition rates, state and input delays have been considered. With utilizing the Lyapunov functional method and free-weighting matrix method, delay-dependent exponential passivity conditions are established. Finally, an illustrative example has been given to demonstrate the effectiveness of the proposed approach.

Acknowledgments

This work was supported in part by the Opening Fund of Geomathematics Key Laboratory of Sichuan Province (scsxdz2011001) and the National Basic Research Program of China (2010CB732501).

References

1 Krasovskii N. N. and Lidskii E. A., Analysis and design of controllers in systems with random attributes, Automatic Remote Control. (1961) 22, 1021–1025.
Google Scholar
2 García-Mora B., Santamaría C., Navarro E., and Rubio G., Modeling bladder cancer using a Markov process with multiple absorbing states, Mathematical and Computer Modelling. (2010) 52, no. 7-8, 977–982, https://doi.org/10.1016/j.mcm.2010.02.036, 2718406, ZBL1205.92035.
10.1016/j.mcm.2010.02.036
Google Scholar
3 Chung K. P., Steady state solution and convergence rate of time-dependent Markov chains of queuing networks, Computers & Mathematics with Applications. (1988) 15, no. 5, 351–358, https://doi.org/10.1016/0898%2D1221(88)90156%2D3, 945807, ZBL0647.60098.
10.1016/0898-1221(88)90156-3
Web of Science® Google Scholar
4 Wang Z., Liu Y., Yu L., and Liu X., Exponential stability of delayed recurrent neural networks with Markovian jumping parameters, Physics Letters A. (2006) 356, no. 4-5, 346–352, 2-s2.0-33745348656, https://doi.org/10.1016/j.physleta.2006.03.078, ZBL1160.37439.
10.1016/j.physleta.2006.03.078
CAS Web of Science® Google Scholar
5 Shi P., Mahmoud M., Nguang S. K., and Ismail A., Robust filtering for jumping systems with mode-dependent delays, Signal Processing. (2006) 86, no. 1, 140–152, 2-s2.0-27944507807, https://doi.org/10.1016/j.sigpro.2005.05.005, ZBL1163.94387.
10.1016/j.sigpro.2005.05.005
Web of Science® Google Scholar
6 Wang Z., Lam J., and Liu X., Robust filtering for discrete-time Markovian jump delay systems, IEEE Signal Processing Letters. (2004) 11, no. 8, 659–662, 2-s2.0-3543117919, https://doi.org/10.1109/LSP.2004.831729.
10.1109/LSP.2004.831729
Web of Science® Google Scholar
7 Ding Q. and Zhong M., On designing H_∞ fault detection filter for markovian jump linear systems with polytopic uncertainties, International Journal of Innovative Computing, Information and Control. (2010) 6, no. 3, 995–1004, 2-s2.0-77950163647.
Web of Science® Google Scholar
8 Zhao X. and Zeng Q., New robust delay-dependent stability and H_∞ analysis for uncertain Markovian jump systems with time-varying delays, Journal of the Franklin Institute. (2010) 347, no. 5, 863–874, https://doi.org/10.1016/j.jfranklin.2010.03.009, 2645396.
10.1016/j.jfranklin.2010.03.009
Web of Science® Google Scholar
9 Zhao X. D. and Zeng Q. S., Delay-dependent stability analysis for Markovian jump systems with interval time-varying-delays, International Journal of Automation and Computing. (2010) 7, no. 2, 224–229, 2-s2.0-77952386251, https://doi.org/10.1007/s11633%2D010%2D0224%2D2.
10.1007/s11633-010-0224-2
Google Scholar
10 Chen B., Li H., Shi P., Lin C., and Zhou Q., Delay-dependent stability analysis and controller synthesis for Markovian jump systems with state and input delays, Information Sciences. (2009) 179, no. 16, 2851–2860, https://doi.org/10.1016/j.ins.2009.04.006, 2547081, ZBL1165.93341.
10.1016/j.ins.2009.04.006
Web of Science® Google Scholar
11 Shu Z., Lam J., and Xiong J., Static output-feedback stabilization of discrete-time Markovian jump linear systems: a system augmentation approach, Automatica. (2010) 46, no. 4, 687–694, 2-s2.0-77949284720, https://doi.org/10.1016/j.automatica.2010.02.001, ZBL1193.93149.
10.1016/j.automatica.2010.02.001
Web of Science® Google Scholar
12 Qiu J. and Lu K., New robust passive stability criteria for uncertain singularly Markov jumpsystems with time delays, ICIC Express Letters. (2009) 3, no. 3, 651–656, 2-s2.0-77953651730.
Google Scholar
13 Kang Y., Zhang J. F., and Ge S. S., Robust output feedback H_∞ control of uncertain Markovian jump systems with mode-dependent time-delays, International Journal of Control. (2008) 81, no. 1, 43–61, https://doi.org/10.1080/00207170701235766, 2369475, ZBL1194.93181.
10.1080/00207170701235766
Web of Science® Google Scholar
14 Boukas E. K. and Liu Z. K., Robust H_∞ control of discrete-time Markovian jump linear systems with mode-dependent time-delays, IEEE Transactions on Automatic Control. (2001) 46, no. 12, 1918–1924, https://doi.org/10.1109/9.975476, 1878213, ZBL1005.93050.
10.1109/9.975476
Web of Science® Google Scholar
15 Chen W.-H., Guan Z.-H., and Yu P., Delay-dependent stability and H_∞ control of uncertain discrete-time Markovian jump systems with mode-dependent time delays, Systems & Control Letters. (2004) 52, no. 5, 361–376, https://doi.org/10.1016/j.sysconle.2004.02.012, 2074379, ZBL1157.93438.
10.1016/j.sysconle.2004.02.012
Web of Science® Google Scholar
16 Shi P., Boukas E.-K., and Agarwal R. K., Control of Markovian jump discrete-time systems with norm bounded uncertainty and unknown delay, IEEE Transactions on Automatic Control. (1999) 44, no. 11, 2139–2144, https://doi.org/10.1109/9.802932, 1735731, ZBL1078.93575.
10.1109/9.802932
Web of Science® Google Scholar
17 Nakura G., Stochastic optimal tracking with preview by state feedback for linear discrete-time markovian jump systems, International Journal of Innovative Computing, Information and Control. (2010) 6, no. 1, 15–28, 2-s2.0-76549097153.
Web of Science® Google Scholar
18 Luan X., Liu F., and Shi P., Neural network based stochastic optimal control for nonlinear Markov jump systems, International Journal of Innovative Computing, Information and Control. (2010) 6, no. 8, 3715–3723, 2-s2.0-77956238294.
Web of Science® Google Scholar
19 Xia Y., Zhu Z., and Mahmoud M. S., H₂ control for networked control systems with Markovian datalosses and delays, ICIC Express Letters. (2009) 3, no. 3, 271–276, 2-s2.0-77953651982.
Google Scholar
20 Senthilkumar T. and Balasubramaniam P., Delay-dependent robust stabilization and H_∞ control for nonlinear stochastic systemswith Markovian jump parameters and interval time-varying delays, Journal of Optimization Theory and Applications. (2011) 151, 100–120, https://doi.org/10.1007/s10957%2D011%2D9858%2D7.
10.1007/s10957-011-9858-7
Web of Science® Google Scholar
21 Zhao X. and Zeng Q., Delay-dependent H_∞ performance analysis for markovian jump systems with mode-dependent time varying delays and partially known transition rates, International Journal of Control, Automation and Systems. (2010) 8, no. 2, 482–489, 2-s2.0-77951165288, https://doi.org/10.1007/s12555%2D010%2D0238%2D0.
10.1007/s12555-010-0238-0
Web of Science® Google Scholar
22 Zhang L. and Boukas E.-K., Stability and stabilization of Markovian jump linear systems with partly unknown transition probabilities, Automatica. (2009) 45, no. 2, 463–468, https://doi.org/10.1016/j.automatica.2008.08.010, 2527344, ZBL1158.93414.
10.1016/j.automatica.2008.08.010
Web of Science® Google Scholar
23 Zhang L., Boukas E.-K., and Lam J., Analysis and synthesis of Markov jump linear systems with time-varying delays and partially known transition probabilities, IEEE Transactions on Automatic Control. (2008) 53, no. 10, 2458–2464, https://doi.org/10.1109/TAC.2008.2007867, 2466607.
10.1109/TAC.2008.2007867
Web of Science® Google Scholar
24 Yin Y., [email protected], Shi P., [email protected], Liu F., and [email protected], Pan J. S., [email protected], Gain-scheduled fault detection on stochastic nonlinear systems with partially known transition jump rates, Nonlinear Analysis. (2011) 13, no. 1, 359–369, https://doi.org/10.1016/j.nonrwa.2011.07.043.
10.1016/j.nonrwa.2011.07.043
Google Scholar
25 Yin Y., Shi P., and Liu F., Gain-scheduled PI tracking control on stochastic nonlinear systems with partially known transition probabilities, Journal of the Franklin Institute. (2011) 348, no. 4, 685–702, https://doi.org/10.1016/j.jfranklin.2011.01.011, 2785448.
10.1016/j.jfranklin.2011.01.011
Web of Science® Google Scholar
26 Luan X. L., Liu F., and Shi P., Finite-time stabilization of stochastic systems with partially known transition probabilities, Journal of Dynamic Systems, Measurement and Control, Transactions of the ASME. (2011) 133, no. 1, 6, 2-s2.0-78650730762, https://doi.org/10.1115/1.4002716, 014504.
10.1115/1.4002716
Web of Science® Google Scholar
27 Zhang L., Boukas E. K., and Shi P., H_∞ model reduction for discrete-time Markov jump linear systems with partially known transition probabilities, International Journal of Control. (2009) 82, no. 2, 343–351, 2-s2.0-60749113963, https://doi.org/10.1080/00207170802098899, ZBL1168.93319.
10.1080/00207170802098899
Web of Science® Google Scholar
28 Balasubramaniam P. and [email protected], Nagamani G., A delay decomposition approach to delay-dependent passivity analysis for interval neural networks with time-varying delay, Neurocomputing. (2011) 74, no. 10, 1646–1653, https://doi.org/10.1016/j.neucom.2011.01.011.
10.1016/j.neucom.2011.01.011
Web of Science® Google Scholar
29 Balasubramaniam P., Nagamani G., and Rakkiyappan R., Global passivity analysis of interval neural networks with discrete and distributed delays of neutral type, Neural Processing Letters. (2010) 32, no. 2, 109–130, 2-s2.0-78049475417, https://doi.org/10.1007/s11063%2D010%2D9147%2D8.
10.1007/s11063-010-9147-8
Web of Science® Google Scholar
30 Balasubramaniam P., Nagamani G., and Rakkiyappan R., Passivity analysis for neural networks of neutral type with Markovian jumping parameters and time delay in the leakage term, Communications in Nonlinear Science and Numerical Simulation. (2011) 16, no. 11, 4422–4437, https://doi.org/10.1016/j.cnsns.2011.03.028, 2806757, ZBL1219.92001.
10.1016/j.cnsns.2011.03.028
Web of Science® Google Scholar
31 Balasubramaniam P. and Nagamani G., Passivity analysis of neural networks with Markovian jumping parameters and interval time-varying delays, Nonlinear Analysis. (2010) 4, no. 4, 853–864, https://doi.org/10.1016/j.nahs.2010.07.002, 2680252, ZBL1208.93124.
10.1016/j.nahs.2010.07.002
Google Scholar
32 Bevelevich V., Classical Network Synthesis, 1968, Van Nostrand, New York, NY, USA.
Google Scholar
33 Balasubramaniam P. and Nagamani G., Global robust passivity analysis for stochastic interval neural networks with interval time-varying delays and Markovian jumping parameters, Journal of Optimization Theory and Applications. (2011) 149, no. 1, 197–215, https://doi.org/10.1007/s10957%2D010%2D9770%2D6, 2774153, ZBL1221.93248.
10.1007/s10957-010-9770-6
Web of Science® Google Scholar
34 Chen Y., Wang H., Xue A., and Lu R., Passivity analysis of stochastic time-delay neural networks, Nonlinear Dynamics. (2010) 61, no. 1-2, 71–82, https://doi.org/10.1007/s11071%2D009%2D9632%2D7, 2661785, ZBL1204.93126.
10.1007/s11071-009-9632-7
Web of Science® Google Scholar
35 Yao X., Wu L., Zheng W. X., and Wang C., Passivity analysis and passification of Markovian jump systems, Circuits, Systems, and Signal Processing. (2010) 29, no. 4, 709–725, https://doi.org/10.1007/s00034%2D010%2D9166%2D8, 2658249, ZBL1196.94032.
10.1007/s00034-010-9166-8
Web of Science® Google Scholar
36 Liang J., Wang Z., and Liu X., Robust passivity and passification of stochastic fuzzy time-delay systems, Information Sciences. (2010) 180, no. 9, 1725–1737, 2-s2.0-76349125529, https://doi.org/10.1016/j.ins.2010.01.003.
10.1016/j.ins.2010.01.003
Web of Science® Google Scholar
37 Li C., Zhang H., and Liao X., Passivity and passification of fuzzy systems with time delays, Computers & Mathematics with Applications. (2006) 52, no. 6-7, 1067–1078, https://doi.org/10.1016/j.camwa.2006.03.029, 2281569, ZBL1122.93368.
10.1016/j.camwa.2006.03.029
Web of Science® Google Scholar
38 Zhu S., Shen Y., and Chen G., Exponential passivity of neural networks with time-varying delay and uncertainty, Physics Letters A. (2010) 375, no. 2, 136–142, https://doi.org/10.1016/j.physleta.2010.10.045, 2737907.
10.1016/j.physleta.2010.10.045
CAS Web of Science® Google Scholar
39 Brogliato B., Lozano R., Maschke B., and Egeland O., Dissipative Systems Analysis and Control: Theory and Applications, 2007, 2nd edition, Springer, London, UK, 2286431.
10.1007/978-1-84628-517-2
Google Scholar
40 Lu C. Y., Tsai H. H., Su T. J., Tsai J. S. H., and Liao C. W., A delay-dependent approach to passivity analysis for uncertain neural networks with time-varying delay, Neural Processing Letters. (2008) 27, no. 3, 237–246, 2-s2.0-42449161839, https://doi.org/10.1007/s11063%2D008%2D9072%2D2.
10.1007/s11063-008-9072-2
Web of Science® Google Scholar
41 Wu H. N. and Cai K. Y., Mode-independent robust stabilization for uncertain Markovian jump nonlinear systems via fuzzy control, IEEE Transactions on Systems, Man, and Cybernetics, Part B. (2006) 36, no. 3, 509–519, 2-s2.0-33744511672, https://doi.org/10.1109/TSMCB.2005.862486.
10.1109/TSMCB.2005.862486
PubMed Web of Science® Google Scholar

All articles

Exponential Passification of Markovian Jump Nonlinear Systems with Partially Known Transition Rates

Abstract

1. Introduction

2. Problem Formulation and Preliminaries

3. Main Results

3.1. Exponential Passivity Analysis

3.2. Exponential Passification

4. Examples

5. Conclusions

Acknowledgments

References

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Exponential Passification of Markovian Jump Nonlinear Systems with Partially Known Transition Rates

Abstract

1. Introduction

2. Problem Formulation and Preliminaries

3. Main Results

3.1. Exponential Passivity Analysis

3.2. Exponential Passification

4. Examples

5. Conclusions

Acknowledgments

References

Figures

References

Related

Information