Volume 2012, Issue 1 949654

Research Article

Open Access

Improving the Solution of Least Squares Support Vector Machines with Application to a Blast Furnace System

Ling Jian,

Corresponding Author

Ling Jian

[email protected]

College of Science, China University of Petroleum, Qingdao 266580, China cup.edu.cn

Search for more papers by this author

Shuqian Shen,

Shuqian Shen

College of Science, China University of Petroleum, Qingdao 266580, China cup.edu.cn

Search for more papers by this author

Yunquan Song,

Yunquan Song

College of Science, China University of Petroleum, Qingdao 266580, China cup.edu.cn

Search for more papers by this author

Ling Jian,

Corresponding Author

Ling Jian

[email protected]

College of Science, China University of Petroleum, Qingdao 266580, China cup.edu.cn

Search for more papers by this author

Shuqian Shen,

Shuqian Shen

College of Science, China University of Petroleum, Qingdao 266580, China cup.edu.cn

Search for more papers by this author

Yunquan Song,

Yunquan Song

College of Science, China University of Petroleum, Qingdao 266580, China cup.edu.cn

Search for more papers by this author

First published: 01 November 2012

https://doi.org/10.1155/2012/949654

Citations: 6

Academic Editor: Chuanhou Gao

Share a link

Email
Wechat
Bluesky

Abstract

The solution of least squares support vector machines (LS-SVMs) is characterized by a specific linear system, that is, a saddle point system. Approaches for its numerical solutions such as conjugate methods Sykens and Vandewalle (1999) and null space methods Chu et al. (2005) have been proposed. To speed up the solution of LS-SVM, this paper employs the minimal residual (MINRES) method to solve the above saddle point system directly. Theoretical analysis indicates that the MINRES method is more efficient than the conjugate gradient method and the null space method for solving the saddle point system. Experiments on benchmark data sets show that compared with mainstream algorithms for LS-SVM, the proposed approach significantly reduces the training time and keeps comparable accuracy. To heel, the LS-SVM based on MINRES method is used to track a practical problem originated from blast furnace iron-making process: changing trend prediction of silicon content in hot metal. The MINRES method-based LS-SVM can effectively perform feature reduction and model selection simultaneously, so it is a practical tool for the silicon trend prediction task.

1. Introduction

As one kernel method, SVM works by embedding the input data x, z ∈ X into a Hilbert space ℋ by a high-dimensional mapping Φ(·), and then trying to find a linear relation among the high-dimensional embedded data points [1, 2]. This process is implicitly performed by specifying a kernel function which satisfies k(x, z) = Φ(x) ^TΦ(z), that is, the inner product of the embedded points. Given observed samples

with size n, SVM formulates the learning problem as a variational problem of finding a decision function f that minimizes the regularized risk functional [3, 4]

(1.1)

where V(·, ·) is called a loss function, λ is the so-called regularization parameter to trade off the empirical risk with the complexity of f, that is, ∥f∥_ℋ, the norm in a reproducing kernel Hilbert space ℋ. By the representer theorem [3, 5], the optimal decision function f satisfying (1.1) has the form

(1.2)

where α_i ∈ ℛ for i = 1, …, n, b ∈ ℛ. This equation can be easily used to tackle a practical problem if the kernel function is specified. To overcome the high computational complexity of traditional SVM, an interesting variant of the standard SVM, least squares support vector machines, has been proposed by Suykens and Vandewalle [6]. In the case of LS-SVM, the inequality constraints in ℓ₂ soft margin SVM are converted into equality constraints. The model training process of LS-SVM is performed by solving a specific linear equations, that is, a saddle point system which can be efficiently solved by iterative methods instead of a quadratic programming problem. Besides computational superiority extensive empirical studies have shown that LS-SVM is comparable to SVM in terms of generalization performance [7]; these features make LS-SVM an attractive algorithm and also a successful alternative to SVM. For the training of the LS-SVM, Van Gestel et al. [7] proposed to reformulate the n + 1 order saddle point system into two n order symmetric positive definite systems which can be solved in turn by the conjugate gradient (CG) algorithm. To speed up the training of LS-SVM, Chu et al. [8] employed the null space method to transform the saddle point system into a reduced n − 1 order symmetric positive definite system which was solved with the CG algorithm also. The minimal residual (MINRES) method proposed by Paige and Saunders is a specialized method for solving a nonsingular symmetric system [9]. This method can avoid the LU factorization and does not suffer from break-down, so it is an efficient numerical method for solving symmetric but indefinite systems. The Karush-Kuhn-Tucker system of LS-SVM is a specified linear system, that is, a saddle point system. Considering the above point, to speed up the solution of LS-SVM model we employ the MINRES method to solve the linear system directly. The main contribution of this paper is to provide a potential alternative to the solution of LS-SVM model. Theoretical analysis of the three numerical algorithms for the solution of LS-SVM model indicates that the MINRES method is the optimal choice. Experiments on benchmark data sets show that compared with the CG method proposed by Suykens et al. and the null space method proposed by Chu et al., the MINRES solver significantly improves the computational efficiency and at the same time keeps almost the same generalized performance with the above two methods. To heel, the MINRES method-based LS-SVM model is constructed and further employed to identify blast furnace (BF) iron-making process, a complex nonlinear system. Practical application to a typical real BF indicates that the established MINRES method-based LS-SVM model is a good candidate to predict the changing trend of the silicon content in BF hot metal with low time cost. The possible application of this work is to aid the BF operators to judge the inner state of BF getting hot or chilling in time properly, which can provide a guide for them to determine the direction of controlling BF in advance. The rest of this paper is organized as follows. In Section 2, we give a review for LS-SVM. Section 3 presents three numerical solutions for LS-SVM. It is followed by extensive experimental validations of the proposed method in Section 4. Section 5 concludes the paper and points out the possible future research.

2. Formulation of LS-SVM

The primal problem of LS-SVM can be formulated following unified format:

(2.1)

for both regression analysis and pattern classification. In (2.1) n is the total number of training samples, x_i is the ith input vector, y_i is the ith output value/label for regression/classification problem, e_i is the ith error variable, C > 0 is the regularization parameter, and b is the bias term. The Lagrangian of (2.1) is given below:

(2.2)

where α_i is the ith Lagrange multiplier. For the convex program (2.1), it is obvious that the Slater constraint qualification holds. Therefore, the optimal solution of (2.1) satisfies its Karush-Kuhn-Tucker system

(2.3)

After eliminating variables w and e the Karush-Kuhn-Tucker system (2.3) can be reformulated following saddle point system [10]:

(2.4)

where K_ij : = k(x_i, x_j) = Φ(x_i) ^TΦ(x_j), I stands for unit matrix, 1_n denotes an n-dimensional vector of all ones, and y = (y₁, …, y_n) ^T.

3. Solution of LS-SVM

In this section, we give a brief review and some analysis of the three mentioned numerical algorithms for solution of LS-SVM.

3.1. Conjugate Gradient Methods

The kernel matrix K is a symmetric positive semidefinite matrix and the diagonal term 1/C is positive, so the matrix H : = K + (1/C)I is symmetric and positive definite. Through the following matrix transformation

(3.1)

where

(3.2)

the saddle point system (2.4) can be factorized into a positive definite system [11]

(3.3)

Suykens et al. suggested the use of the CG method for the solution of (3.3) and proposed to solve two n order positive definite systems. More exactly, their algorithm can be described as follows.

Step 1. Employ the CG algorithm to solve the linear equations Hη = 1_n and get the intermediate variable η.

Step 2. Solve the intermediate variable μ from Hμ = y by the CG method.

Step 3. Obtain Lagrange dual variables α = μ − bη and bias term .

The output of any new data x can subsequently be deduced by computing the decision function .

3.2. Null Space Methods

In what was mentioned previously, to get the intermediate variable η and μ two n order positive definite systems need to be solved by CG methods. Chu et al. [8] proposed an interesting method to the numerical solution of LS-SVM by solving one n − 1 order reduced system of linear equations. The improved method suggested by Chu et al. can be seen as one kind of null space method. The saddle point system (2.4) can be written as

(3.4)

Chu et al. specified a particular solution of 1_nα = 0 as

and the null space of 1_nα = 0 as

(3.5)

Through solving the following reduced system of order n − 1 for the auxiliary unknown ν,

(3.6)

the solution of the saddle point system (2.4) can be obtained as α = Zν and

3.3. Minimal Residual Methods

The vector sequences in the CG method correspond to a factorization of a tridiagonal matrix similar to the coefficient matrix. Therefore, a breakdown of the algorithm can occur corresponding to a zero pivot if the matrix is indefinite. Furthermore, for indefinite matrices the minimization property of the CG method is no longer well defined. The MINRES method proposed by Paige and Saunders [9] is a variant of the CG method that avoids the LU factorization and does not suffer from breakdown. It minimizes the residual in the ℓ₂-norm which is an efficient numerical algorithm for solving symmetric but indefinite systems; the corresponding convergence behavior of the MINRES method for indefinite systems has been analyzed by Van der Vorst [12]. The purpose of this paper is to employ the MINRES method to solve the saddle point system (2.4) directly. Next we gave a brief review of the MINRES algorithm. Let x₀ be an initial guess for the solution of the symmetric indefinite linear system Ax = b. One can obtain the iterative sequence x_m, m = 1,2, … such that

(3.7)

where r_m = b − Ax_m is the mth residual for m = 1,2, …, and

(3.8)

is the mth Krylov subspace. Lanczos methods can be used to generate an orthonormal basis of 𝒦_m(A, r₀), and then only two basis vectors are needed to compute x_m; see, for example, [12]. The detailed implementation of the MINRES algorithm can be found in [12].

It has been shown that rounding errors are propagated to the approximate solution with a factor proportional to the square of the condition number of coefficient matrix [12]; one should be careful with the MINRES method for ill-conditioned systems.

3.4. Some Analysis on These Three Numerical Algorithms

The properties of short recurrences and optimization [12] make the CG method the first choice for the solution of a symmetric positive definite system. Suykens et al. transformed the n + 1 order saddle point system (2.4) into two n order positive definite systems which are solved by CG methods. However, it is time consuming to solve two n order positive definite systems with large scales. To overcome this shortcoming, Chu et al. [8] transformed equivalently the original n + 1 order system into an n order symmetric positive definite system, and then the CG method can be used. This method can be seen as a null space method. Unfortunately, the transformation may destroy heavily the sparse structure and increase greatly the condition number of the original system. This can hugely slow down the convergence rate of the CG algorithm. Theoretical analysis about the influence of the transformation on the condition number is indispensable, but it is rather difficult. We leave it as an open problem. In this paper, the MINRES method is directly applied to solve the original saddle point problem of n + 1 order. Similar to the CG method, the MINRES method also has properties of short recurrences and optimization.

In light of the analysis mentioned above, the MINRES method should be the first choice for the solution of LS-SVM model, since it avoids solving two linear systems and destroying the sparse structure of the original saddle point system simultaneously.

4. Numerical Implementations

4.1. Experiments on Benchmark Data Sets

In this section we give the experimental test results on the accuracy and efficiency of our method. For comparison purpose, we implement the CG method proposed by Suykens and Vandewalle [6] and the null space method suggested by Chu et al. [8]. All experiments are implemented with MATLAB version 7.8 programming environment running on an IBM compatible PC under Window XP operating system, which is configured with Intel Core 2.1 Ghz CPU and 2 G RAM. The generalized used Gaussian RBF kernel k(x, z) = exp (−∥x − z∥²/σ²) is selected as the kernel function. We use the default setting for kernel width σ², that is, set kernel width as the dimension of inputs.

We first compare three algorithms on three benchmark data sets: Boston, Concrete, and Abalone, which are download from UCI [13]. Each data set is randomly partitioned into 70% training and 30% test sets. We also list the condition numbers of coefficients matrices solved by three methods for the analysis of the computing efficiencies. As shown in Tables 1–3 the condition number for the CG method is the least one and the condition number for the null space method significantly increases.

Table 1. Experimental results of three methods on Boston data set.

	Boston data set, 506 samples, 13-d inputs, σ² equals 13
log₂C	Conjugate gradient method			Null space method			MINRES method
	Cond^†	CPU^‡	MSE*	Cond	CPU	MSE	Cond	CPU	MSE
−5	4	0.3281	49.1027	366.9451	0.8438	49.1027	45.6283	0.2500	49.1027
−4	8	0.4688	39.4132	369.0926	0.6250	39.4132	31.6150	0.3438	39.4132
−3	15	0.3438	29.7686	388.1770	0.7656	29.7686	26.3388	0.3125	29.7686
−2	28	0.4531	24.2532	460.1920	0.7656	24.2532	29.2813	0.3281	24.2532
−1	60	0.2500	21.0322	474.6254	1.0625	21.0322	61.3493	0.4219	21.0322
0	116	0.3438	15.5875	566.2504	1.2500	15.5875	119.071	0.1875	15.5875
1	234	0.7188	13.6449	946.4564	1.1250	13.6449	239.374	0.4375	13.6449
2	472	0.9531	13.0252	1945.300	1.0625	13.0252	482.447	0.6875	13.0252
3	924	0.9375	10.9810	2244.342	1.4063	10.9810	944.042	0.6406	10.9810
4	1734	1.3594	10.3168	5229.460	1.2500	10.3168	1776.31	0.8906	10.3168
5	3801	1.5469	10.2063	10785.92	1.4844	10.2063	3876.97	1.1406	10.2063
6	7530	2.0469	11.3937	24998.71	1.9063	11.3937	7682.07	1.2969	11.3937
7	14618	2.4531	11.7750	47781.41	2.2188	11.7750	14932.2	1.6875	11.7750
8	29769	3.0625	12.9925	61351.85	2.9844	12.9925	30382.8	2.3750	12.9925
9	58387	3.4063	14.0194	101181.8	3.5938	14.0194	59619.0	2.6875	14.0194
10	119285	4.0313	17.2330	285440.0	4.8281	17.2330	121708	3.5313	17.2330

Cond^† denotes the condition number, CPU^‡ stands for running time, MSE* is mean square error.

Table 2. Experimental results of three methods on Concrete data set.

	Concrete data set, 1030 samples, 8-d inputs, σ² equals 8
log₂C	Conjugate gradient method			Null space method			MINRES method
	Cond	CPU	MSE	Cond	CPU	MSE	Cond	CPU	MSE
−5	7	2.0781	140.8498	738.137223	3.6719	140.8498	51.5204280	1.6406	140.8498
−4	13	2.3594	111.2384	745.054714	3.6563	111.2384	39.7005872	1.8906	111.2383
−3	25	2.8125	89.3458	796.627246	3.8281	89.3458	31.7895802	2.0938	89.3459
−2	50	2.4844	74.4146	850.938881	3.9688	74.4146	51.4318149	2.0469	74.4146
−1	102	3.0000	60.2984	954.604170	4.3906	60.2984	104.293122	2.2969	60.2984
0	199	3.4219	50.4491	1397.13474	4.8438	50.4491	202.202543	2.8281	50.4490
1	399	4.0625	43.5416	1737.97400	5.7188	43.5416	406.110983	3.2500	43.5416
2	787	4.8750	41.5463	2369.65769	6.4219	41.5463	799.643656	3.8594	41.5463
3	1561	6.3125	36.5797	5375.87469	7.3750	36.5797	1586.70628	4.2500	36.5797
4	3197	8.0000	33.4861	7342.75323	8.7188	33.4861	3247.47638	5.0156	33.4861
5	6411	10.3281	33.1452	18274.6591	10.8438	33.1452	6510.73913	6.2188	33.1452
6	12530	13.8750	33.4936	37192.6189	12.9063	33.4936	12732.7611	8.2813	33.4936
7	25614	18.5781	33.8690	73008.8645	15.8594	33.8690	26010.1838	11.0156	33.8690
8	51260	25.1250	32.6925	126475.189	19.5938	32.6925	52056.7280	14.8906	32.6925
9	101053	33.9531	35.1044	249234.605	25.2969	35.1044	102657.615	19.9219	35.1043
10	199734	46.3125	40.4777	557864.123	32.9219	40.4777	202961.396	27.0625	40.4777

Table 3. Experimental results of three methods on Abalone data set.

	Abalone data set, 4177 samples, 7-d inputs, σ² equals 7
log₂C	Conjugate gradient method			Null space method			MINRES method
	Cond	CPU	MSE	Cond	CPU	MSE	Cond	CPU	MSE
−5	42.341	20.343	5.3623	2955.9655	39.7344	5.3623	369.9433	12.9531	5.3623
−4	84.059	22.984	5.1143	3028.4495	41.1406	5.1143	332.0862	14.2344	5.1143
−3	167.846	26.343	4.7978	3043.4615	42.6719	4.7978	306.5691	16.0156	4.7978
−2	337.691	33.281	4.6923	3567.1431	46.8125	4.6923	338.1679	18.4688	4.6923
−1	666.823	39.315	4.4360	4888.3227	50.8438	4.4360	667.7842	22.3125	4.4360
0	1327.351	47.531	4.4744	5355.5805	54.6563	4.4744	1329.291	26.2656	4.4744
1	2700.547	58.015	4.4217	9894.2450	59.8438	4.4217	2704.345	34.1719	4.4217
2	5275.703	74.859	4.3948	8239.2388	69.2031	4.3948	5283.506	42.5469	4.3948
3	10709.216	94.765	4.4169	18279.897	80.4219	4.4169	10724.46	54.7813	4.4169
4	21357.750	124.359	4.5053	24472.420	97.7500	4.5053	21388.43	71.3906	4.5053
5	42427.822	177.171	4.6144	105161.60	133.2656	4.6144	42489.70	103.6406	4.6144
6	85153.757	221.468	4.6857	185913.18	155.9219	4.6857	85276.97	129.3750	4.6857
7	171369.064	312.078	4.7145	212162.90	212.4531	4.7145	171614.1	181.8750	4.7145
8	344731.082	430.640	4.8621	705659.56	289.4531	4.8621	345216.0	260.5469	4.8621
9	681509.920	602.765	5.2294	1162595.7	395.6250	5.2294	682494.5	360.5625	5.2294
10	1363883.053	840.625	5.6517	3106655.0	549.4844	5.6517	1365853	488.6250	5.6517

The columns of Cond in Tables 1, 2, and 3 show that compared with the CG method the condition number for the MINRES method increases a bit, but much less than the condition number of the null space method. The orders of linear equations solved by the CG method, the null space method, and the MINRES method are n, n − 1, and n + 1, respectively. The condition numbers for the CG method and the MINRES method are very close, but we have to solve two systems of n − 1 order using CG methods. Hence, the running time of the MINRES method should be less than that of the CG method. CPU column in Tables 1–3 shows that the MINRES method-based LS-SVM model costs much less running time than the CG method and the null space method-based LS-SVM model in all cases of setting C. So the MINRES method-based LS-SVM model is a preferable algorithm for solving LS-SVM model. In the next subsection, we will employ the MINRES method-based LS-SVM model to solve a practical problem.

4.2. Application on Blast Furnace System

Blast furnace, one kind of metallurgical reactor used for producing pig iron, is often called hot metal. The chemical reactions and heat transport phenomena take place throughout the furnace as the solid materials move downwards and hot combustion gases flow upwards. The main principle involved in the BF iron-making process is the thermochemical reduction of iron oxide ore by carbon monoxide. During the iron-making period, a great deal of heat energy is produced which can heat up the BF temperature approaching 2000°C. The end products consisting of slag and hot metal sink to the bottom and are tapped periodically for the subsequent refining. It will take about 6–8 h for a cycle of iron-making [11]. BF iron-making process is a highly complex nonlinear process with the characteristics of high temperature, high pressure, concurrence of transport phenomena, and chemical reactions. The complexity of the BF and the occurrence of a variety of process disturbances have been obstacles for the adoption of modeling and control in the process. Generally speaking, to control a BF system often means to control the hot metal temperature and components, such as silicon content, sulfur content in hot metal, and carbon content in hot metal within acceptable bounds. Among these indicators, the silicon content often acts as a chief indicator to represent the thermal state of the BF, an increasing silicon content meaning a heating of the BF while a decreasing silicon content indicating a cooling of the BF [11, 14]. Thus, the silicon content is a reliable measure of the thermal state of the BF, and it becomes a key stage to predict the silicon content for regulating the thermal state of the BF. Therefore, it has been the active research issue to build silicon prediction model in the recent decades, including numerical prediction models [15] and trend prediction models [11].

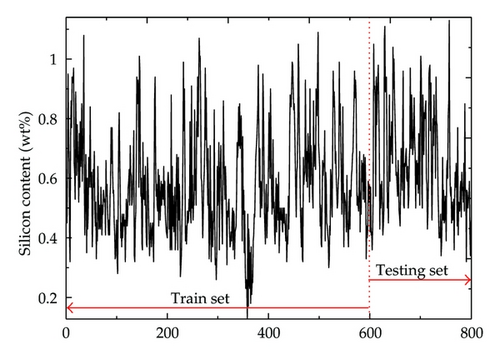
In this subsection, the tendency prediction of silicon content in hot metal is transformed as a binary classification problem. Samples with increasing silicon content are denoted by +1 whereas a decreasing silicon content is denoted by −1. In the present work, the experimental data is collected from a medium-sized BF with the inner volume of about 2500 m³. The variables closely related to the silicon content are measured as the candidate inputs for modeling. Table 4 presents the variables information from the studied BF. There are totally 801 data points collected with the first 601 points as train set and the residual 200 points as testing set. The sampling interval is about 1.5 h for the current BF. Figure 1 illustrates the evolution of the silicon content in hot metal.

Table 4. A list of input variables.

Variable name [unit]	Abbreviation	Range	F-score	Mean accuracy
Latest silicon content (wt%)	Si	0.13–1.13	0.1269	81.786%
Sulfur content (wt%)	S	0.012–0.077	0.0570	82.857%
Basicity of ingredients (wt%)	BI	0.665–1.609	0.0229	81.786%
Feed speed (mm/h)	FS	16.725–297.510	0.0132	83.214%
Blast volume (m³/min)	BV	1454.30–5580.200	0.0054	83.747%
CO₂ percentage in top gas (wt%)	CO₂	7.921–22.892	0.0048	83.750%
Pulverized coal injection (ton)	PCI	0.230–98.533	0.0037	83.214%
CO percentage in top gas (wt%)	CO	9.267–27.374	0.0036	82.500%
Blast temperature (°C)	BT	1086.100–1239.700	0.0031	83.571%
Oxygen enrichment percentage (wt%)	OEP	−0.001–14.688	0.0019	83.393%
H₂ percentage in top gas (wt%)	H₂	2.564–4.065	0.0005	83.214%
Coke load of ingredients (wt%)	CLI	2.032–5.071	0.0004	82.857%
Furnace top temperature (°C)	TP	62.703–264.130	0.0002	82.679%
Blast pressure (kPa)	BP	59.585–367.780	0.0001	83.214%
Furnace top pressure (kPa)	TP	8.585–199.790	0.0001	82.679%

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Evolution of silicon content in hot metal.

There are in total 15 candidate variables listed in Table 4 from which to select model inputs. Generally, too many input parameters will increase the complexity of model while too little inputs will reduce the accuracy of model. A tradeoff has to be taken between the model complexity and accuracy when selecting the inputs. Therefore, it is necessary to screen out less important variables as inputs from these 15 candidate variables. Here, the inputs are screened out by an integrative way that combines F-score method [16] for variables ranking and cross-validation method for variables and model parameters selection.

F-score is an effective tool for feature selection in data mining and can give feature ranking by evaluating the discrimination of two sets with real values. For those 15 candidate variables in Table 4, their F-scores are defined as follows:

(4.1)

where

and

stand for the mean of the ith attribute of the whole training, positive and negative examples, respectively, while

and

are the ith variable of the jth positive and negative instance, respectively. Hence, a variable ranking can be achieved through F-score method. Table 4 gives the results of F-scores of all 15 variables, which are ranked according to the F-score values. As one kernel-based learning model, the kernel parameter σ², and regularized parameter C play an important role in LS-SVM, so one should pay attention to selecting proper parameters. Grid search-based ten-fold cross-validation is executed on the train set for searching the optimal (σ²,C). The searching grid for model parameters is set as

(4.2)

Mean accuracy in Table 4 stands for the average accuracy under ten-fold cross-validation experiments of LS-SVM model on some grid points with the best performance. In the current work, we first select the variable with highest F-score as model input and then add variables one by one according to their F-scores. Mean accuracy under all kinds of input variables can be achieved and the results are shown in Table 4. The following are shown by the mean accuracy column: (1) at the beginning, the mean accuracy increases gradually as more candidate variables are taken as model inputs; (2) the largest mean accuracy appears when CO₂ is included within the input set; (3) when the mean accuracy is beyond the maximum, it will fluctuate as the residual variables are added by turns into the input set. These results indicate that, as the studied BF is concerned, the optimal input set is [Si, S, BI, FS, BV, CO₂] with the model parameters setting (σ², C) = (2⁹, 2⁸). Table 5 lists the LS-SVM model accuracy including with/without feature and model selection versions on testing set. In the case of without feature and model selection version, all candidate variables are selected as inputs, and we use the default setting for LS-SVM model; that is, set kernel width σ² equal to the dimension of input variable and set regularized parameter C as 1. The information in the second row of this table, such as 34/42, denotes that there are 42 times predicted results that are ascending trend, and 34 times predictions are successful. The confidence level of the LS-SVM model without model and feature selection fluctuates severely between the ascending and descending prediction from 80.95% to 58.86%. The difference of confidence levels of LS-SVM model with model and feature selection between ascending and descending prediction is reduced to 2.19% indicating that model and feature selection procedure enhances the stability of the LS-SVM model obviously. As the last column of Table 5 shows, TSA of LS-SVM model with feature and model selection procedure is significantly improved compared with LS-SVM model without feature and model selection, so the selection procedure is indispensable for the current practical application. Table 6 lists the running time of three mentioned numerical algorithms when performing feature and model selection procedure. The cost time of the MINRES method is reduced significantly compared with the other algorithms. In a word, the feature and model selection procedure can be effectively performed for the MINRES method-based LS-SVM, and it is meaningful for practical using.

Table 5. Predictive results of LS-SVM model with/without feature and model selection.

Inputs	(σ²,C)	Ascend (99*)	Descend (101)	TSA^†
15	(15, 1)	34/42 = 80.95%	93/158 = 58.86%	127/200 = 63.5%
6	(2⁹, 2⁸)	73/94 = 77.66%	80/106 = 75.47%	153/200 = 76.5%

99* means 99 observations are ascending trend; TSA^† stands for testing set accuracy.

Table 6. Running time of three numerical methods on model identification.

Algorithm	Conjugate gradient method	Null space method	MINRES method
CPU	1948	2800	1488

5. Conclusions and Points of Possible Future Research

In this paper, we have proposed an alternative, that is, the MINRES method, to the solution of LS-SVM model which is formulated as a saddle point system. Numerical experiments on UCI benchmark data sets show that the proposed numerical solution method of LS-SVM model is more efficient than the algorithms proposed by Suykens and Vandewalle [6] and Chu et al. [8]. To heel, the MINRES method-based LS-SVM model including feature selection from extensive candidate and model parameter selection is proposed and employed for the silicon content trend prediction task. The practical application to a typical real BF indicates that the proposed MINRES method-based LS-SVM model is a good candidate to predict the trend of silicon content in BF hot metal with low running time.

However, it should be pointed out that despite the MINRES method-based LS-SVM model displaying low running time, lack of metallurgical information may be the root to the limited accuracy of the current prediction model. So there is much work worth investigating in the future to further improve the model accuracy and increase the model transparency, such as constructing predictive model by integrating domain knowledge and extracting rules. The extracted rules can account for the output results with detailed and definite inputs information, which may further serve for the control purpose by linking the output results with controlled variables. These investigations are deemed to be helpful to further improve the efficiency of predictive model.

Acknowledgment

This work was partially supported by National Natural Science Foundation of China under Grant no. 11126084, Natural Science Foundation of Shandong Province under Grant no. ZR2011AQ003, Fundamental Research Funds for the Central Universities under Grant no. 12CX04082A, and Public Benefit Technologies R&D Program of Science and Technology Department of Zhejiang Province under Grant No. 2011C31G2010136.

References

1 Vapnik V. N., The Nature of Statistical Learning Theory, 2000, 2nd edition, Springer-Verlag, New York, NY, USA, 1719582, ZBL0934.62009.
10.1007/978-1-4757-3264-1
Google Scholar
2 Schölkopf B. and Smola A., Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond, 2002, MIT Press, Cambridge, Mass, USA.
Google Scholar
3 Evgeniou T., Pontil M., and Poggio T., Regularization networks and support vector machines, Advances in Computational Mathematics. (2000) 13, no. 1, 1–50, https://doi.org/10.1023/A:1018946025316, 1759187, ZBL0939.68098.
10.1023/A:1018946025316
Web of Science® Google Scholar
4 Cristianini N. and Shawe-Taylor J., An Introduction to Support Vector Machines, 2000, Cambridge University, Cambridge, UK.
Google Scholar
5 Bishop C. M., Pattern Recognition and Machine Learning, 2006, 4, Springer, New York, NY, USA, https://doi.org/10.1007/978%2D0%2D387%2D45528%2D0, 2247587.
10.1007/978-0-387-45528-0
Google Scholar
6 Suykens J. A. K. and Vandewalle J., Least squares support vector machine classifiers, Neural Processing Letters. (1999) 9, no. 3, 293–300, 2-s2.0-0032638628.
10.1023/A:1018628609742
Web of Science® Google Scholar
7 Van Gestel T., Suykens J. A. K., Baesens B., Viaene S., Vanthienen J., Dedene G., De Moor B., and Vandewalle J., Benchmarking least squares support vector machine classifiers, Machine Learning. (2004) 54, no. 1, 5–32, 2-s2.0-0242288903, https://doi.org/10.1023/B:MACH.0000008082.80494.e0.
10.1023/B:MACH.0000008082.80494.e0
Web of Science® Google Scholar
8 Chu W., Ong C. J., and Keerthi S. S., An improved conjugate gradient scheme to the solution of least squares SVM, IEEE Transactions on Neural Networks. (2005) 16, no. 2, 498–501, 2-s2.0-15344351150, https://doi.org/10.1109/TNN.2004.841785.
10.1109/TNN.2004.841785
PubMed Google Scholar
9 Paige C. C. and Saunders M. A., Solutions of sparse indefinite systems of linear equations, SIAM Journal on Numerical Analysis. (1975) 12, no. 4, 617–629, 0383715, https://doi.org/10.1137/0712047.
10.1137/0712047
Web of Science® Google Scholar
10 Jian L., Gao C., Li L., and Zeng J., Application of least squares support vector machines to predict the silicon content in blast furnace hot metal, ISIJ International. (2008) 48, no. 11, 1659–1661, 2-s2.0-59649118425, https://doi.org/10.2355/isijinternational.48.1659.
10.2355/isijinternational.48.1659
CAS Web of Science® Google Scholar
11 Gao C., Jian L., and Luo S., Modeling of the thermal state change of blast furnace hearth with support vector machines, IEEE Transactions on Industrial Electronics. (2012) 59, no. 2, 1134–1145, https://doi.org/10.1109/TIE.2011.2159693.
10.1109/TIE.2011.2159693
Web of Science® Google Scholar
12 van der Vorst H. A., Iterative Krylov Methods for Large Linear Systems, 2003, 13, Cambridge University Press, Cambridge, UK, https://doi.org/10.1017/CBO9780511615115, 1990752.
10.1017/CBO9780511615115
Google Scholar
13 Blake C. and Merz C., Uci repository of machine learning databases, 1998.
Google Scholar
14 Gao C., Chen J. L., Zeng J., Liu X., and Sun Y., A chaos-based iterated multistep predictor for blast furnace ironmaking process, AIChE Journal. (2009) 55, no. 4, 947–962, 2-s2.0-65349142587, https://doi.org/10.1002/aic.11724.
10.1002/aic.11724
CAS Web of Science® Google Scholar
15 Jian L., Gao C., and Xia Z., A sliding-window smooth support vector regression model for nonlinear blast furnace system, Steel Research International. (2011) 82, no. 3, 169–179, 2-s2.0-79952205822, https://doi.org/10.1002/srin.201000082.
10.1002/srin.201000082
CAS Web of Science® Google Scholar
16 Chen Y. W. and Lin C. J., Combining SVMs with various feature selection strategies, Studies in Fuzziness and Soft Computing. (2006) 207, 315–324, 2-s2.0-34047138318.
10.1007/978-3-540-35488-8_13
Google Scholar

Citing Literature

All articles

Improving the Solution of Least Squares Support Vector Machines with Application to a Blast Furnace System

Abstract

1. Introduction

2. Formulation of LS-SVM