A posteriori error estimates for the generalized overlapping domain decomposition method (GODDM) (i.e., with Robin boundary conditions on the interfaces), for second order boundary value problems, are derived. We show that the error estimate in the continuous case depends on the differences of the traces of the subdomain solutions on the interfaces. After discretization of the domain by finite elements we use the techniques of the residual a posteriori error analysis to get an a posteriori error estimate for the discrete solutions on subdomains. The results of some numerical experiments are presented to support the theory.

1. Introduction

We consider the generalized overlapping domain decomposition method that is, with Robin transmission conditions on the interfaces [1, 2] for second order boundary value problems on a bounded domain Ω with Dirichlet boundary conditions. The a priori estimate of the error is given in several papers, see for instance Lions [3] in which a variational formulation of the classical Schwarz method is derived. In Chan et al. [4] a geometry related convergence results are obtained. Douglas and Huang [1] studied the accelerated version of the GODDM, Engquist and Zhao [2] studied the convergence for simple (rectangular or circular) geometries; however, these authors did not give a criterion to stop the iterative process. All these results can also be found in the recent books on domain decomposition methods of Quarteroni and Valli [5], Toselli and Widlund [6]. Recently Maday and Magoulès [7, 8] presented an improved version of the Schwarz method for highly heterogeneous media. This method uses new optimized interface conditions specially designed to take into account the heterogeneity between the subdomains on the interfaces. A recent overview of the current state of the art on domain decomposition methods can be found in two special issues of the computer methods in applied mechanics and engineering journal, edited by Farhat and Le Tallec [9], Magoulès and Rixen [10] and in Nataf [11].

In general, the a priori estimate is not suitable for assessing the quality of the approximate solution on subdomains since it depends mainly on the exact solution itself which is unknown. The alternative approach is to use the approximate solution itself in order to find such an estimate. This approach, known as a posteriori estimate, became very popular in the nineties of the last century with finite element methods, see the monographs [12, 13] and the references therein. In their paper Otto and Lube [14] gave an a posteriori estimate for a nonoverlapping domain decomposition algorithm that said that “the better the local solutions fit together at the interface the better the errors of the subdomain solutions will be.” This error estimate enables us to know with certainty when one must stop the iterative process as soon as the required global precision is reached. A posteriori error analysis was also used by Bernardi et al. [15] to determine an optimal value of the penalty parameter for penalty domain decomposition methods to construct fast solvers.

In various situations it is better to use overlapping decompositions for faster convergence rate, for example, the case of decomposition into simple subdomains where uniform discretizations are possible. So the aim of this paper is to show that a similar result to that in [14], in the case of the GODDM, holds. It is obtained via the introduction of two auxiliary problems defined each over two nonoverlapping subdomains. These auxiliary problems are needed for the analysis and not for the computation.

The paper is organized as follows. In Section 1, we introduce some necessary notations, then we give a variational formulation of our model problem. We establish, in Section 2, a stopping criterion for the iterative process in the continuous case. In Section 3, an a posteriori error estimate is proposed for the convergence of the discretized solution using the finite element method on subdomains. We conclude this section by an adaptation of the techniques of the residual a posteriori error analysis to give an a posteriori estimate in the discrete case.

1.1. Problem Formulation and Domain Decomposition Method

Let Ω be a bounded domain in ℝ² with a piecewise C^1,1 boundary ∂Ω. We denote (·, ·) _Ω and ∥·∥_0,Ω the usual inner product and norm of L²(Ω). Let H¹(Ω) be the usual Sobolev space with norm ∥·∥_1,Ω and seminorm | · |_1,Ω; is the subspace of functions of H¹(Ω) vanishing on ∂Ω.

Let Ω₁ and Ω₂ be two subdomains of Ω (to be defined later), when Γ_i ⊂ ∂Ω_i we need the space

which is a subspace of H^1/2(Γ_i); i = 1,2 equipped with the norm

()

On the subdomain Ω_i we use the space

which has as a trace space

, i = 1,2. By

we denote the inner product of L²(Γ_i).

Let us consider the following model problem:

()

The variational formulation of this problem is given by

()

where a(u, v) = ∫_Ω ∇u∇v dx and(f, v) _Ω = ∫_Ω fv dx for all

. We split the domain Ω into two overlapping subdomains Ω₁ and Ω₂ such that

()

The generalized overlapping domain decomposition method is written as follows: set

in Ω_i and construct the sequence

, i = 1,2 in parallel for n = 0,1, 2, …

()

where η_i is the exterior normal to Ω_i and α_i is a real parameter, i = 1,2.

The convergence of the GODDM (1.5) and (1.6) is proved in [2, 5]. Our main interest is to obtain an a posteriori error estimate we need for stopping the iterative process as soon as the required global precision is reached.

The weak formulations of problems (1.5), (1.6) are given, respectively, by

()

where V_i is defined above. It can also be written as

()

2. A Posteriori Error Estimate in the Continuous Case

Since it is numerically easier to compare the subdomain solutions on the interfaces Γ₁ and Γ₂ rather than on the overlap Ω₁₂, thus we need to introduce two auxiliary problems defined on nonoverlapping subdomains of Ω. This idea allows us to obtain the a posteriori error estimate by following the steps of Otto and Lube [14]. We get these auxiliary problems by coupling each one of the problems (1.5) and (1.6) with another problem in a nonoverlapping way over Ω. These auxiliary problems are needed for the analysis and not for the computation, to get the estimate. We see that we can go from the GODDM to a couple of nonoverlapping domain decomposition methods with Robin boundary conditions on the interfaces Γ₁ and Γ₂. To define these auxiliary problems we need to split the domain Ω into two sets of disjoint subdomains: (Ω₁, Ω₃) and (Ω₂, Ω₄), see Figure 1, such that

()

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

Two examples of domain decompositions (Schur and Schwarz).

Let

be the solutions of problems (1.5), (1.6). We define the couple

over (Ω₁, Ω₃) to be the solution of the following nonoverlapping problems:

()

We can write

on Γ₁ (in the 3rd equation in (2.2)) that is,

is the difference between the overlapping and the nonoverlapping solutions

and

(in problems (1.5)-(1.6) and (2.2)-(2.3), resp.) in Ω₃. Because both overlapping and nonoverlapping problems converge, see [2, 5] that is,

and

tend to

should tend to naught an n tends to infinity in V₂.

By multiplying the first equation in (2.2) by v₁ ∈ V₁ and integrating by parts we obtain

()

where

is given by

()

On the other hand, using the last equation in (2.3) and putting

()

we get

()

where

. From this result we can write the following algorithm which is equivalent to the auxiliary nonoverlapping problem (2.2)-(2.3). We need this algorithm and two lemmas for obtaining an a posteriori error estimate for this problem.

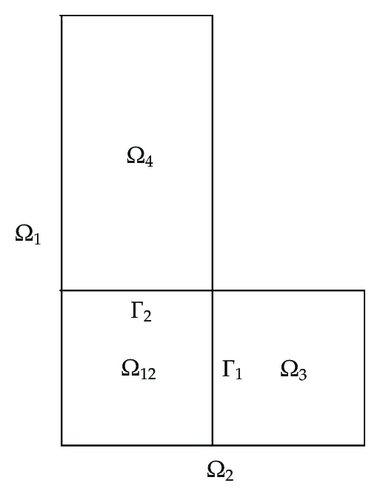
Algorithm 2.1. The sequences solutions of problems (2.2), (2.3) satisfy the following domain decomposition algorithm denoted ALG.G.D.D.M.

(1)
Let be an initial value, is the dual of W₁).
(2)
Given solve for i = 1,3, i ≠ j: Find solutions of
()
(3)
Compute new data , i = 1,3 from
()
(4)
Set n = n + 1, go to Step 2.

Lemma 2.2. Let , and . Then for i = 1,3, i ≠ j, the following relations hold

()

The proof follows directly from steps 2 and 3 of ALG.G.D.D.M.

Lemma 2.3. By letting C be a generic constant which has different values at different places one get for i = 1,3, i ≠ j

()

Proof. Using (2.10) and the fact that the trace mapping Tr_i : V_i → W_i and its inverse are continuous, we obtain

()

On the otherhand we have

()

This ends the proof.

Based on the previous two lemmas, we can obtain the following a posteriori error estimate for the nonoverlapping domain decomposition problem (2.2)-(2.3).

Proposition 2.4. For the sequences solutions of problems (2.2), (2.3) one has the following a posteriori error estimation

()

Proof. From (2.10) and (2.11) we have

()

Taking

and

, then using Lemma 2.3 we get

()

which is the required result.

In the similar way, we define another nonoverlapping auxiliary problem over (Ω₂, Ω₄). The sequences

are solutions of

()

where we can write

on Γ₂ (in the 3rd equation in (2.18)) that is,

is the difference between the overlapping and the nonoverlapping solutions

and

(in problems (1.5)-(1.6) and (2.18)-(2.19) resp.) in Ω₄. As both sequences

and

converge towards u₁,

should tend to naught as n tends to infinity. Using Lemmas 2.2 and 2.3 over (Ω₂, Ω₄) we obtain the a posteriori error estimate for this auxiliary problem.

Proposition 2.5. For the sequences solutions of problems (2.18), (2.19) one has the following a posteriori error estimate

()

Remark 2.6. We remark from Propositions 2.4 and 2.5 that we can go from sequences of solutions to problems (1.5) and (1.6) to sequences of solutions to problems generated by nonoverlapping domain decomposition problems of Robin type transmission conditions across the interfaces Γ₁ and Γ₂. This result enable us to compare the subdomain iterations of the GODDM on the interfaces Γ₁ and Γ₂ rather than on the overlap region Ω₁₂.

In the following theorem we are going to use this fact to obtain an a posteriori error estimate for the continuous generalized overlapping domain decomposition method (1.5)-(1.6).

Theorem 2.7. Let where u is the solution of problem (1.2). For the sequences solutions of problems (1.5) and (1.6), one has the following a posteriori error estimate

()

Proof. We use two auxiliary problems defined each over two nonoverlapping subdomains of Ω. These two problems are defined over (Ω₁, Ω₃) and (Ω₂, Ω₄), respectively. From the previous two propositions we have

()

From the definitions of

and

, we have

()

which is the required result.

3. A Posteriori Error Estimate in the Discrete Case

In this section, we consider the discretization of the variational problems (1.7) and (1.8). Let τ_h be a triangulation of Ω compatible with the decomposition and V_h ⊂ V is the subspace of continuous functions (polynomials of degree k, k ≥ 1) which vanish over ∂Ω. We have

()

W_i,h is a subspace of

which consists of continuous piecewise polynomial functions on Γ_i which vanish at the end points of Γ_i (i = 1,2).

Let u_h ∈ V_h be the solution of the discrete problem associated with (1.3),

. We construct the sequences

solutions of the discrete versions of (1.5) and (1.6) at the (n + 1)th iteration, that is,

()

In a similar manner to that of Section 2, we introduce two discrete auxiliary problems, one over (Ω₁, Ω₃), the other over (Ω₂, Ω₄). We let

()

We can write

on Γ_1, (in the 3rd equation in (3.4)), that is,

is the difference between the discrete overlapping and the nonoverlapping solutions

and

(in problems (3.2)-(3.3) and (3.4)-(3.5) resp.,) in Ω₃. Because both

and

converges to

should tend to naught as n tends to infinity.

Similarly, over (Ω₂, Ω₄) we consider the sequences

solutions of the following discrete problems:

()

where we can also write

on Γ_2,,

tends to naught as n tends to infinity as explained for the previous problems. We can obtain the discrete counterparts of Propositions 2.4 and 2.5 by doing almost the same analysis as in Section 2 (i.e., passing from continuous spaces to discrete subspaces and from continuous sequences to discrete ones). Therefore

()

where the discrete trace subspace norm

defined over Γ_i (i = 1,2) is taken to be

()

Hence, using the previous two inequalities, we have

()

We remark that (3.10) is the discrete version of (2.21).

Remark 3.1. Let us note that (3.10) is an estimate of the error between the approximate solution u_i,h and the approximate solution of the discretized overlapping domain decomposition algorithm .

Next we will obtain an estimate of the error between the approximate solution and the exact solution u. We introduce some necessary notations. We denote by

()

For every T ∈ τ_h and E ∈ ε_h, we define

()

For a function f which is not necessarily continuous across two neighboring elements of τ_h having E as a common side, [f] denotes the jump of f across E and η_E the normal vector of E.

We have the following theorem which gives the a posteriori error estimate for the discrete GODDM.

Theorem 3.2. Let where u is the solution of problem (1.2), the sequences are solutions of problems (3.2)-(3.3). Then there exists a constant C independent of h such that

()

where

()

The symbol * corresponds to n + 1 when i = 1 and to n when i = 2.

Proof. The proof is based on the technique of the residual a posteriori estimation (see [13]) and Theorem 2.7. We give the main steps. By the triangle inequality we have

()

The second term on the right-hand side of (3.15) is bounded as in (3.10) by

()

To bound the first term on the r.h.s of (3.15) we use the residual equation and apply the technique of the residual a posteriori error estimation, see [13], to get for v_h ∈ V_h and

()

where f_h is any approximation of f by polynomials of degree at most k, therefore

()

We use the fact that

()

Finally, by combining (3.15), (3.18), and (3.19) the required result follows.

3.1. Numerical Examples

As an illustration of the theoretical results obtained in this article and to be able to use the a posteriori error estimate (3.10), we consider the following problem

()

with Ω = ]0,1[² for the first and second examples and Ω = ]0,1[×]0, 1/2[∪]0, 1/2[×]0,1[ for the third example (i.e., an L-shaped region). The exact solution is taken to be u(x, y) = xy(x − 1)(y − 1)e^xy for the first example, u(x, y) = sin 8πx · sin 8πy for the second example, and finally u(x, y) = xy(x − 1)(y − 1)(x − 1/2)(y − 1/2) for the third example.

We first compute the bilinear Galerkin solution u_h over Ω and then apply the generalized overlapping domain decomposition method (1.7)-(1.8) to compute the bilinear sequences

to be able to look at the behavior of the constant C within (3.10) as the mesh size becomes small (h⁻¹ = 8,16,32,64). We take Ω₁ = ]0, 3/4[×]0,1[ and Ω₂ = ]1/4, 1[×]0,1[ for the first and second examples. As for the third example we have Ω₁ = ]0,1[×]0, 1/2[ and Ω₂ = ]0, 1/2[×]0,1[. We denote by

()

The generalized overlapping domain decomposition method, with α₁ = α₂ = 0.5, converges. The iterations have been stopped when the relative error between two subsequent iterates is less than ϵ = 10⁻⁶.

The Quotient in Tables 1, 2, 3, 4, 5, and 6 represents an estimate of the constant C in (3.10). It happens to tend to a constant value around 1 which what we expect (i.e., we have asymptotic exactness). We present, for each example, results with and without the a posteriori estimate as a stopping criteria. We see that we obtain the same results but with less iterations when using the a posteriori estimate as a stopping criteria for a moderately small mesh size for the first and third examples. But for the second example, the difference in iteration count is clear between the two approaches.

Table 1. Results on the square without a posteriori estimates as a stopping criteria for the first example.

h	1/8	1/16	1/32	1/64
Er₁	1.7957693(−02)	8.1821001(−03)	4.5210766(−03)	3.1683034(−03)
Er₂	1.0956427(−02)	9.6854433(−03)	8.7326244(−03)	6.9200024(−03)
Trer₁	2.2513498(−02)	0.1504199(−02)	8.1897348(−03)	3.4817880(−02)
Trer₂	1.7198801(−02)	2.1677755(−02)	9.3967836(−03)	6.9538120(−03)
Iterations	12	10	7	5
Quotient	0.7280898	0.7507522	0.7536285	0.9667203

Table 2. Results on the square with a posteriori estimates as a stopping criteria for the first example.

h	1/8	1/16	1/32	1/64
Er₁	1.3457623(−02)	4.1221001(−03)	8.5210766(−03)	3.1683034(−03)
Er₂	1.0556422(−02)	5.2454431(−03)	8.4322244(−03)	6.2200024(−03)
Trer₁	2.2513498(−02)	5.1504199(−03)	2.1897348(−02)	3.4817880(−03)
Trer₂	2.4423401(−02)	6.1677755(−03)	1.3967836(−03)	6.9538120(−03)
Iterations	3	5	6	7
Quotient	0.5116240	0.7276534	0.7277927	0.8996421

Table 3. Results on the square without a posteriori estimates as a stopping criteria for the second example.

h	1/8	1/16	1/32	1/64
Er₁	1.7957693(−02)	2.5598288(−03)	4.7627655(−03)	0.8936322(−04)
Er₂	1.0956427(−02)	4.5353208(−02)	8.1970235(−03)	6.3020810(−03)
Trer₁	2.2513498(−02)	5.2993342(−02)	1.1897348(−02)	3.4817880(−03)
Trer₂	1.7198801(−08)	6.0068501(−09)	1.3967836(−08)	6.9538120(−08)
Iterations	10	9	7	5
Quotient	0.7280898	0.9041330	1.089299	1.560316

Table 4. Results on the square with a posteriori estimates as a stopping criteria for the second example.

h	1/8	1/16	1/32	1/64
Er₁	4.7345582(−02)	8.1821001(−04)	4.8510591(−03)	1.4817880(−02)
Er₂	1.3897220(−02)	9.6854433(−02)	8.1924358(−03)	6.9200024(−03)
Trer₁	9.6471474(−02)	0.1504199(−02)	1.1897348(−02)	1.4817880(−02)
Trer₂	9.1859622(−09)	0.0000000(+00)	0.3967836(−09)	2.9538120(−08)
Iterations	8	6	5	4
Quotient	0.6348280	0.6493334	1.096336	1.018248

Table 5. Results on the L-shaped region without a posteriori estimates as a stopping criteria.

h	1/8	1/16	1/32	1/64
Er₁	3.5915386(−02)	16.3642002(−03)	9.0421132(−03)	6.3366068(−03)
Er₂	2.19128497(−02)	19.3708866(−03)	12.4732488(−03)	9.8440048(−03)
Trer₁	4.50217996(−02)	0.2008398(−02)	4.3794696(−02)	2.9635760(−02)
Trer₂	3.4397602(−02)	4.3355510(−02)	2.7935672(−03)	5.9076240(−03)
Iterations	10	8	6	6
Quotient	0.5443332	0.6562642	0.8380865	1.008344

Table 6. Results on the L-shaped region with a posteriori estimates as a stopping criteria.

h	1/8	1/16	1/32	1/64
Er₁	2.5815386(−02)	14.3642002(−03)	9.0421132(−03)	4.3366122(−03)
Er₂	2.19128487(−02)	12.3708866(−03)	12.4732488(−03)	6.8440223(−03)
Trer₁	4.60217446(−02)	0.4008398(−02)	4.3794696(−02)	4.8635660(−03)
Trer₂	3.3397402(−02)	2.3355510(−02)	2.7935672(−03)	6.8076220(−03)
Iterations	4	5	6	7
Quotient	0.6009663	0.9170200	0.8380865	0.9579689

3.2. Concluding Remarks

(1)
From Theorem 3.2 we see that the subdomain errors depend on the differences of the latter on the interface, on the data f, and on the approximate solution u^h. The first two terms of (3.13) are the contribution to the a posteriori error from the finite element discretization whereas the last term is the domain decomposition error. Numerical results indicate that the finite element part of the error estimate dominates the domain decomposition part.
(2)
As far as the asymptotic exactness of the estimator based on (3.13) is concerned, Ainsworth and Oden in [12, Theorem 3.5] gave a necessary condition for this property to hold. This condition says that the local residuals in (3.13) should be computed exactly.
(3)
The a posteriori error analysis for a second order boundary value problem or Stokes problem is possible. Also, similar results can be obtained in the general case of more than two subdomains.

References

1 Douglas,J.Jr. and Huang C.-S., An accelerated domain decomposition procedure based on Robin transmission conditions, BIT Numerical Mathematics. (1997) 37, no. 3, 678–686, https://doi.org/10.1007/BF02510246, 1483680, ZBL0886.65114.
10.1007/BF02510246
Web of Science® Google Scholar
2 Engquist B. and Zhao H.-K., Absorbing boundary conditions for domain decomposition, Applied Numerical Mathematics. (1998) 27, no. 4, 341–365, https://doi.org/10.1016/S0168%2D9274(98)00019%2D1, 1644668, ZBL0952.65098.
10.1016/S0168-9274(98)00019-1
Web of Science® Google Scholar
3 Lions P.-L., R. Glowinski, G. H. Golub, G. A. Meurant, and J. Périaux, On the Schwarz alternating method. I, First International Symposium on Domain Decomposition Methods for Partial Differential Equations, 1988, SIAM, Philadelphia, Pa, USA, 1–42, 972510, ZBL0658.65090.
Google Scholar
4 Chan T. F., Hou T. Y., and Lions P.-L., Geometry related convergence results for domain decomposition algorithms, SIAM Journal on Numerical Analysis. (1991) 28, no. 2, 378–391, https://doi.org/10.1137/0728021, 1087510, ZBL0724.65109.
10.1137/0728021
Web of Science® Google Scholar
5 Quarteroni A. and Valli A., Domain Decomposition Methods for Partial Differential Equations, 1999, The Clarendon Press, Oxford, UK, 1857663.
10.1093/oso/9780198501787.001.0001
Google Scholar
6 Toselli A. and Widlund O., Domain Decomposition Methods—Algorithms and Theory, 2005, 34, Springer, Berlin, Germany, Springer Series in Computational Mathematics, 2104179.
10.1007/b137868
Google Scholar
7 Maday Y. and Magoulès F., Improved ad hoc interface conditions for Schwarz solution procedure tuned to highly heterogeneous media, Applied Mathematical Modelling. (2006) 30, no. 8, 731–743, https://doi.org/10.1016/j.apm.2005.05.020.
10.1016/j.apm.2005.05.020
Web of Science® Google Scholar
8 Maday Y. and Magoulès F., A survey of various absorbing interface conditions for the Schwarz algorithm tuned to highly heterogeneous media, Domain Decomposition Methods: Theory and Applications, 2006, 25, Gakkōtosho, Tokyo, Japan, 65–93, Gakuto International Series. Mathematical Sciences Applications, 2233439, ZBL1103.65124.
Google Scholar
9 Farhat C. and Le Tallec P., Vista in Domain Decomposition Methods, Computer Methods in Applied Mechanics and Engineering. (2000) 184, no. 2-4, 143–520.
10.1016/S0045-7825(99)00226-1
Google Scholar
10 Magoulès F. and Rixen D., Domain decomposition methods: recent advances and new challenges in engineering, Computer Methods in Applied Mechanics and Engineering. (2007) 196, no. 8, 1345–1346, https://doi.org/10.1016/j.cma.2006.09.003, 2277020.
10.1016/j.cma.2006.09.003
Web of Science® Google Scholar
11 Nataf F., Recent developments on optimized Schwarz methods, Domain Decomposition Methods in Science and Engineering XVI, 2007, 55, Springer, Berlin, Germany, 115–125, Lecture Notes in Computational Science and Engineering, https://doi.org/10.1007/978%2D3%2D540%2D34469%2D8_10, 2334096.
10.1007/978-3-540-34469-8_10
Google Scholar
12 Ainsworth M. and Oden J. T., A Posteriori Error Estimation in Finite Element Analysis, 2000, Wiley-Interscience, New York, NY, USA, https://doi.org/10.1002/9781118032824, 1885308, ZBL1049.65135.
10.1002/9781118032824
Google Scholar
13 Verfürth A., A Review of a Posteriori Error Estimation and Adaptive Mesh-Refinement Techniques, 1996, Wiley Teubner, Stuttgart, Germany.
Google Scholar
14 Otto F.-C. and Lube G., A posteriori estimates for a non-overlapping domain decomposition method, Computing. (1999) 62, no. 1, 27–43, https://doi.org/10.1007/s006070050011, 1680737, ZBL0936.65116.
10.1007/s006070050011
Web of Science® Google Scholar
15 Bernardi C., Chacón Rebollo T., Chacón Vera E., and Franco Coronil D., A posteriori error analysis for two-overlapping domain decomposition techniques, Applied Numerical Mathematics. (2009) 59, no. 6, 1214–1236, https://doi.org/10.1016/j.apnum.2008.06.004, 2510489.
10.1016/j.apnum.2008.06.004
Web of Science® Google Scholar

Citing Literature

All articles

A Posteriori Error Estimates for the Generalized Overlapping Domain Decomposition Methods

Abstract

1. Introduction

1.1. Problem Formulation and Domain Decomposition Method

2. A Posteriori Error Estimate in the Continuous Case

3. A Posteriori Error Estimate in the Discrete Case

3.1. Numerical Examples

3.2. Concluding Remarks

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Posteriori Error Estimates for the Generalized Overlapping Domain Decomposition Methods

Abstract

1. Introduction

1.1. Problem Formulation and Domain Decomposition Method

2. A Posteriori Error Estimate in the Continuous Case

3. A Posteriori Error Estimate in the Discrete Case

3.1. Numerical Examples

3.2. Concluding Remarks

References

Citing Literature

Figures

References

Related

Information