Journal of Applied Mathematics
Volume 2012, Issue 1 924765
Research Article
Open Access

Differential Quadrature Solution of Hyperbolic Telegraph Equation

B. Pekmen, 

Corresponding Author

B. Pekmen

Institute of Applied Mathematics, Middle East Technical University, 06800 Ankara, Turkey metu.edu.tr

Department of Mathematics, Atilim University, 06836 Ankara, Turkey atilim.edu.tr

Search for more papers by this author
M. Tezer-Sezgin, 

M. Tezer-Sezgin

Institute of Applied Mathematics, Middle East Technical University, 06800 Ankara, Turkey metu.edu.tr

Department of Mathematics, Middle East Technical University, 06800 Ankara, Turkey metu.edu.tr

Search for more papers by this author
First published: 31 July 2012
https://doi.org/10.1155/2012/924765
Citations: 11
Academic Editor: Roberto Barrio

Abstract

Differential quadrature method (DQM) is proposed for the numerical solution of one- and two-space dimensional hyperbolic telegraph equation subject to appropriate initial and boundary conditions. Both polynomial-based differential quadrature (PDQ) and Fourier-based differential quadrature (FDQ) are used in space directions while PDQ is made use of in time direction. Numerical solution is obtained by using Gauss-Chebyshev-Lobatto grid points in space intervals and equally spaced and/or GCL grid points for the time interval. DQM in time direction gives the solution directly at a required time level or steady state without the need of iteration. DQM also has the advantage of giving quite good accuracy with considerably small number of discretization points both in space and time direction.

1. Introduction

Consider the second-order linear hyperbolic telegraph equation in one-dimensional space:
()
and the second-order two-dimensional hyperbolic telegraph equation:
()
where Ω1 = [a < x < b]×[t > 0] and Ω2 = [0 < x, y < 1]×[t > 0].
The hyperbolic differential equations are the basis for fundamental equations of atomic physics and commonly used in signal analysis for transmission and propagation of electrical signals. Equations (1.1)-(1.2) are damped wave equations for α > 0,   β = 0 of which the solution is of great importance in wave phenomena and telegraph equation for α ≥ β > 0. The initial conditions are assumed to be
()
with Dirichlet type boundary conditions
()
or Neumann type boundary conditions
()
for (1.1), and
()
with the boundary conditions
()
or
()
for (1.2).

The functions f(x, t), h1(t), h2(t), v1(x), v2(x), k1(t), k2(t) are continuous functions defined on Ω1, and similarly g(x, y, t), ϕ1(x, y), ϕ2(x, y), p1(x, y, t), p2(x, y, t), p3(x, y, t) are defined and continuous on Ω2.

For one-dimensional telegraph equation there are several studies which give numerical solutions. Mohebbi and Dehghan [1] give a compact finite difference approximation of fourth order in space and use collocation method for the time direction. For large values of time level they are forced to increase the degree of polynomial in collocation approach to obtain accurate results. In [2], a scheme similar to finite difference method is proposed using collocation points and approximating the solution with thin plate splines radial basis functions. Dehghan and Lakestani [3] and Saadatmandi and Dehghan [4] make use of Chebyshev cardinal functions and shifted Chebyshev polynomials, respectively, for expanding the approximate solution of one-dimensional hyperbolic telegraph equation. In [4], the advantage is obtaining the closed form of the approximate solution. Dehghan and Ghesmati [5] have applied also dual reciprocity boundary element method (DRBEM) for solving second-order one-dimensional hyperbolic telegraph equation. For time discretization, Crank-Nicolson finite difference has been used, and the solution has been obtained iteratively.

Dehghan and Mohebbi [6] have used the same idea given in [1] for solving the two-dimensional linear hyperbolic telegraph equation which is the combination of finite difference in space and collocation in time directions. In [7], Mohanty and Jain introduced a new unconditionally stable alternating direction implicit (ADI) scheme of second order accurate for two-dimensional telegraph equation. The solution is progressed in time direction by splitting the systems in x- and y-directions and solving two systems for each time level. Mohanty [8] and Mohanty et al. [9] extended their studies for linear hyperbolic equations with variable coefficients in two-space dimensions. Mohanty [10] and Mohanty et al. [11] extended also ADI method solution procedure to two- and three-space dimensional telegraph equations. Ding and Zhang [12] proposed a three-level compact difference scheme of fourth order for the solution of two-dimensional, second-order, nonhomogenous linear hyperbolic equation for positive coefficients. Meshless method has also been used by Dehghan and Ghesmati [13] and Dehghan and Shokri [14] for solving two-dimensional telegraph equation. The conventional moving least squares approximation is exploited in order to interpolate the solution by using monomials from the Pascal triangle in [13], and thin plate splines radial basis functions are used for the approximation of the solution in [14]. In both of these studies, another time integration scheme has been used (finite difference) for time derivatives, and the solutions are obtained iteratively.

The usage of DQM in both space and time directions is encountered in [15]. The authors proposed to solve time-dependent problems (first order time derivatives) by a block-marching methodology in time direction. In each time block, DQM is applied both in space and time directions. The novelty of this approach is in the higher order of accuracy and less computational effort compared to 4-stage Runge-Kutta method.

In this paper, we employ the differential quadrature method in both time and space directions to obtain numerical solutions of one- and two-dimensional linear hyperbolic telegraph equations which contain second-order time derivatives. The use of DQM in time direction, which also discretizes the initial condition ut, automatically results in an overdetermined system. The numerical scheme then provides the solution at any time level without an iteration. This makes the main difference from the conventional time integration methods. The solution is obtained directly at all required time levels by solving one overdetermined system which contains the solution at the grid points in space and time directions. The Gauss-Chebyshev-Lobatto (GCL) points are used in space direction whereas either equally spaced or GCL grid points can be taken in time direction. The numerical procedure requires very small number of grid points in space directions and appropriate number of time grid points for reaching a certain time level.

The organization of the paper is as follows. In Section 2, we introduce the polynomial and Fourier-based DQM and discuss the formulation of the method both in time and space directions for (1.1)-(1.2). In Section 3, we discuss the accuracy and efficiency of the proposed method applying to some test problems in one- and two-dimensional cases. Section 4 gives the conclusion about the findings.

2. Method of Solution

2.1. Differential Quadrature Method

The differential quadrature method approximates the derivative of a function at a grid point by a linear summation of all the functional values in the whole computational domain.

When the function f(x) is approximated by a high-order polynomial, Shu [16] presented some explicit formulations to compute the weighting coefficients. The weighting coefficients in that weighted sum are determined using the Lagrange interpolation polynomial which has no limitation on the choice of the grid points. This leads to the polynomial-based differential quadrature method (PDQ). When Fourier series expansion is used, Fourier expansion-based differential quadrature (FDQ) is presented.

Suppose the degree of the polynomial is N − 1, then a single variable function f(x) and its first- and second-order derivatives can be approximated at a grid point xi by PDQ approach as
()
where i, j = 1,2, …, N and N is the number of grid points in the whole (one-dimensional) domain, and wj(x) are the Lagrange interpolated polynomials. The weighting coefficients for the first-order derivative are [16]
()
()
where
()
The weighting coefficients for the second-order derivative are given in terms of weighting coefficients for the first-order derivatives as
()
()
As it can be seen from these equations, there is a recurrence relationship for the second and so higher-order derivatives.
When the function f(x) on any interval [a, b] is approximated by a Fourier series expansion in the form
()
the Lagrange interpolated trigonometric polynomials are taken as
()
where
()
Thus, we can write
()
In FDQ approach for nonperiodic problems, weighting coefficients for the first- and second-order derivatives are, respectively:
()
where i, j = 1,2, …, N.
Different grid distributions may be chosen. In this study, we choose the Gauss-Chebyshev-Lobatto (GCL) grid points in space direction which are clustered through the end points and equally spaced (ES) or GCL grid points in time direction. GCL points are the extremal values of Chebyshev polynomials −1 ≤ Tk(x) ≤ 1 and are defined as
()
in [−1,1] where k is the degree of the Chebyshev polynomial.

2.2. Application of DQM To Time and Space Directions for Hyperbolic Telegraph Equation

Application to one- and two-dimensional hyperbolic telegraph equations is going to be shown using PDQ method. FDQ application will be similar, the only difference being in the weighting coefficients.

2.2.1. One-Dimensional Hyperbolic Telegraph Equation

PDQ approximations for the derivatives in (1.1) can be written as
()
where i = 1,2, …, N;   l = 1,2, …, L, N and L are the number of discretization points, and aik, bik, and , are the weighting coefficients for the first- and second-order derivatives, in space and time directions, respectively. These coefficients are computed by (2.2a)–(2.4b) when PDQ is used. Therefore, (1.1) will be discretized as
()
where i = 1,2, …, N and l = 1,2, …, L.
GCL grids in x-space on an interval [a, b] are computed as
()
In time direction, equally spaced (ES) grid points on an interval [0, T] as
()
are used.
The main system equation (2.12) may be denoted as an algebraic system
()
where u is the unknown vector to be determined with the entries at the grid points (xi, tl), and the matrix [B] consists of the known weighting coefficients. The known vector f contains the function values f(xi, tl) as entries. The initial condition u(x, 0) = v1(x) is inserted to the system (2.15) directly modifying the matrix [B] and the vector f. The other initial condition ut(x, 0) is expanded by DQM formulation as
()
Equation (2.16) will also be a system which can be described as
()
where the matrix [B0] and the vector {v2} contain coefficients and v2(xi) as entries.

If the Dirichlet type boundary conditions are given, these conditions are directly inserted to (2.15) and (2.17) with the given initial conditions u(x, 0). So, the coefficient matrices [B] and [B0] will be of size (N − 2)(L − 1)×(N − 2)(L − 1) and (N − 2)×(N − 2)(L − 1), respectively.

The systems (2.15) and (2.17) form an overdetermined system. Therefore, least square method or QR factorization will be made use of for obtaining the solution vector {u}.

If the Neumann type boundary conditions are given, the sizes of the new coefficient matrix [Bneu] in (2.15) and in (2.17) will be (L − 1)N × (L − 1)N and N × (L − 1)N, respectively. Neumann boundary conditions are also discretized using PDQ as
()
which can be formed as system
()
where is a matrix of size 2(L − 1)×(L − 1)N containing the coefficients a1k, aNk and the vector {k} contains k1(ti), k2(ti) as entries. Then, the whole system (2.15) with [Bneu], (2.17) with and (2.19) again is an overdetermined system which will be solved either by QR or least square method.
Also, the ordering of the unknown vector is important since the structure of [B] or [Bneu] depends on this ordering. To get a well-conditioned matrix [B], the order of the unknown vector {u} is arranged as
()
where i = 2,3, …, N − 1 if boundary conditions are Dirichlet type and i = 1,2, …, N if Neumann type boundary conditions are given.

2.2.2. Two-Dimensional Hyperbolic Telegraph Equation

The space and time derivatives in (1.2) can be discretized by using PDQ as
()
and the discretized form of (1.2) takes the form
()
where N, M, L are the number of discretization points in x, y, t directions and i = 1,2, …, N;   j = 1,2, …, M;   l = 1,2, …, L, respectively.
GCL grids for x- and y-spaces are taken as
()
when 0 ≤ x, y ≤ 1. Furthermore, time direction is divided equally as in (2.14) or by GCL grid points on an interval [0, T] as
()
The initial condition ut(x, y, 0) and the Neumann type boundary conditions are added to the system equation (2.22) discretizing them using PDQ approximations as follows:
()

As in one-dimensional telegraph equation, the DQM discretized system (2.22) will be solved together with the initial and boundary conditions. If the boundary conditions are of Dirichlet type, they will be inserted to the overdetermined system (2.22) combined with the system resulting from initial conditions. For Neumann boundary conditions, the system (2.22) and (2.25) will be solved together.

One of the difficulties in two-dimensional hyperbolic telegraph equation is that the system to be solved becomes larger as N, M, L are increased. This causes more memory and CPU usage. To overcome this problem, the system is reduced by removing the entries on the coefficient matrix of the system which correspond to known information (e.g., initial condition u(x, y, 0) and the Dirichlet type boundary conditions). Meanwhile, the right hand side of the reduced system is also modified taking into account removed known entries in the coefficient matrix.

The order of the unknown vector u in this case is organized to get a well-conditioned system. Consider the unknown vector as a matrix U whose each row entry corresponds to a time level. Notationally,
()
where j = 1,2, …, M, and the matrix of size L × NM will be rewritten as a vector writing columns consecutively.

The solution will be obtained by solving only one system with the initial and boundary conditions being all inserted, and the aforementioned reduction of known entries is performed to reduce the size of the system. The solution vector contains all required time level values in it.

The solvability of the overdetermined system of equations depends on the column rank of the coefficient matrix which is NML in this case. When the initial and/or Neumann type boundary conditions are discretized using DQM, and added to the system, the row size is certainly greater than NML which makes the system overdetermined. The choice of the grid points in both space and time domains affects the stability of the system. As mentioned in the Shu’s book [16], the solution with GCL grid points becomes more stable than equally spaced grid points in both space and time directions. Moreover, appropriate choice of N, M, and L makes the final coefficient matrix full column rank.

3. Numerical Results

The discretization is performed by taking N, M GCL grid points in x- and y-directions. When equally spaced points are taken in time direction on [0, T],
()
in which T is the required uptime level.
To measure the accuracy of the method, we use the following errors which can be defined as [3, 13]
()
where nod is the total number of all grid points in space direction, and the errors can be computed at any time level.

We present some numerical results of one- and two-dimensional hyperbolic telegraph equation for different α and β values to observe the accuracy and efficiency of the DQ method. Exact solutions of the test problems are available. Thus, the variations of RMS and relative errors can be obtained for discussing accuracy of DQM solutions.

3.1. Problem 1

We consider the one-dimensional hyperbolic telegraph equation (1.1) in the interval 0 ≤ x ≤ 2π, 0 < t ≤ 3 with α = 4,   β = 2. The exact solution is taken as [2]
()
In this case, f(x, t) = (2 − 2α + β2)e−tsin (x). The initial conditions are given as
()
We solve the equation first by taking Dirichlet type boundary conditions and then with the Neumann type boundary conditions. The Dirichlet type boundary conditions from the exact solution are
()
The Neumann type boundary conditions are
()

Table 1 shows RMS errors obtained by using Dirichlet type boundary conditions with different Δt (equally spaced time grid is used) values. It is noticed that 10−5 accuracy is achieved even with a coarse mesh (Δt = 0.5) in time direction. It is improved with a finer mesh (Δt = 0.25).

Table 1. RMS errors for Problem 1 with N = 11 using Dirichlet boundary conditions.
t Δt = 0.25 Δt = 0.5
0.5 8.57e − 07 6.20e − 05
1 3.94e − 07 3.90e − 05
2 1.66e − 07 3.00e − 05
3 6.23e − 08 2.93e − 05

Table 2 reports RMS errors obtained by using Neumann boundary conditions with different number of discretization points in [0,2π]. As can be seen from Table 2, increasing N from 11 to 21 improves the results in terms of accuracy, which was dropped with Neumann boundary conditions being used, with Δt = 0.25. Table 3 gives RMS errors when FDQ weighting coefficients are used in space direction and PDQ weighting coefficients in time direction for the same Neumann problem. For this particular problem, the accuracy of the results by using FDQ even with N = 11 doubled from the accuracy of the results obtained by PDQ.

Table 2. RMS errors for Problem 1 with Δt = 0.25 using PDQ with Neumann boundary conditions.
t N = 11 N = 13 N = 17
0.5 2.82e − 05 7.74e − 07 2.26e − 10
1 1.52e − 05 3.78e − 07 1.45e − 10
2 4.44e − 06 1.41e − 07 8.32e − 11
3 3.09e − 06 7.63e − 08 5.72e − 11
Table 3. RMS errors for Problem 1 with N = 11 using FDQ with Neumann boundary conditions.
t Δt = 0.25
0.5 1.79e − 10
1 1.39e − 10
2 8.03e − 11
3 5.53e − 11

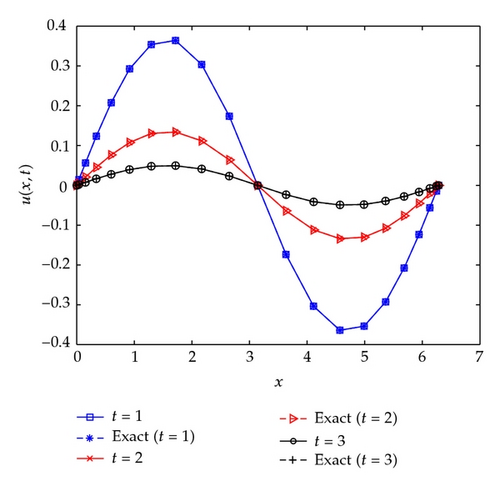
Figure 1 depicts the very well agreement of DQM and exact solutions at different time levels; even equally spaced time grid points are used. The number of GCL grid points in space is small (N = 21), and Δt = 0.25 is considerably large compared to other time integration schemes.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
Numerical and exact solutions at different times for Problem 1, with Δt = 0.25, N = 17 using Neumann boundary conditions.

3.2. Problem 2

We consider now two-dimensional telegraph equation (1.2) in the region 0 ≤ x, y ≤ 1, t > 0, with α = β = 1. The analytical solution given by [13] is
()
with the initial conditions
()
and the boundary conditions are Dirichlet type
()
We extract g(x, y, t) from the analytical solution as
()

Tables 4 and 5 present the comparison of the DQM solution and the exact solution in terms of relative errors for different Δt values when equally spaced time grid points are used. In this two-dimensional problem, FDQ approximation for space derivatives, keeping PDQ approximation for time derivatives, is also studied. As can be seen from the Tables 4 and 5, both PDQ and FDQ approximations in space directions give almost the same accuracy even with coarse grids (Δt = 0.5 and Δt = 0.25) taking a little more space grid points in FDQ. Furthermore, as L is increased (Δt is decreased), the accuracy is increased.

Table 4. Relative errors of Problem 2 with N = M = 17 using PDQ.
t Δt = 0.25 Δt = 0.5
0.5 1.18e − 09 8.80e − 05
1 1.11e − 09 5.94e − 05
2 4.28e − 10 9.17e − 05
3 1.36e − 10 1.09e − 04
Table 5. Relative errors of Problem 2 using N = M = 21 using FDQ.
t Δt = 0.25 Δt = 0.5
0.5 3.62e − 09 8.93e − 05
1 3.62e − 09 6.03e − 05
2 3.43e − 09 9.31e − 05
3 3.66e − 09 1.10e − 04

3.3. Problem 3

In this case, (1.2) is taken with α = β = 1 and α = 5,   β = 1 in the region 0 ≤ x,   y ≤ 1,   t > 0. The analytical solution is given by [6]
()
with the initial conditions
()
and the boundary conditions are of Dirichlet and Neumann type on the walls parallel to each other:
()
The inhomogeneity is extracted from the exact solution as
()

Relative errors between numerical solution (PDQ) and exact solution for different Δt values are presented in Table 6. Even with a large Δt = 1, about 10−4 accuracy is reached. As Δt is decreased, accuracy is increased as expected. In Table 7, the error decreases with a higher α value. Again, it is noticed that with considerably small number of grid points both in space direction (N = M = 11) and time direction (Δt = 0.5  or  Δt = 0.25), at least 10−6 accuracy is obtained.

Table 6. Relative errors of Problem 3 with N = M = 11,   α = β = 1.
t Δt = 0.25 Δt = 0.5 Δt = 1
1 9.65e − 08 6.55e − 05 1.18e − 03
3 8.24e − 09 9.65e − 07 2.60e − 04
5 1.53e − 08 1.04e − 05 5.68e − 04
Table 7. Relative errors of Problem 3 with N = M = 11,   α = 5,   β = 1.
t Δt = 0.25 Δt = 0.5
1 5.02e − 08 9.67e − 06
3 7.75e − 09 2.03e − 06
5 2.69e − 08 9.64e − 06

3.4. Problem 4

Consider the homogenous (g(x, y, t) = 0) (1.2) in the region 0 ≤ x,   y ≤ 1,   t > 0, with α = 1 + π2,   β = 1. The exact solution is given by [12]
()
with the initial conditions
()
and Dirichlet and Neumann boundary conditions on parallel walls are
()

Table 8 compares the numerical solution (both PDQ and FDQ) with the exact solution for different time levels in terms of RMS errors. FDQ weighting coefficients are used in space directions remaining PDQ weighting coefficients in time direction (FDQ-PDQ) and PDQ approximation is used in both directions (PDQ-PDQ). In this problem, we use GCL grid points in both space and time directions. FDQ-PDQ approximation gives better accuracy than PDQ-PDQ approximation for this problem.

Table 8. RMS errors for u(x, t) of Problem 5 using M = N = 11, L = 13.
t PDQ-PDQ FDQ-PDQ
0.75 1.31e − 09 1.38e − 11
2.25 1.04e − 09 9.40e − 12
3 6.71e − 10 7.74e − 12

To emphasize the importance of the GCL grid points in time direction, we present RMS errors versus the number of grid points in time direction in Figures 2 and 3. The number of GCL grid points in space direction (N = M = 11) at T = 3 is fixed, and only PDQ-PDQ approximation is considered. When the number of equally spaced points in time exceeds 28, the system becomes rank deficient. This means that large number of ES grid points in time direction causes unstable solution. On the other hand, GCL grid points in time direction still give very good accuracy for 11 ≤ L ≤ 41 as can be seen in Figure 3. Moreover, RMS error using 11 to 23 ES grid points increases faster than RMS error using the same number of GCL grid points in time. The accuracy with GCL grid points in time direction remains in a scale between 0.2   ×   10−9 and 1.8   ×   10−9.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
RMS errors at T versus ES grid points in time direction for Problem 4.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
RMS errors at T versus ES grid points in time direction for Problem 4.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
RMS errors at T versus GCL grid points in time direction for Problem 4.

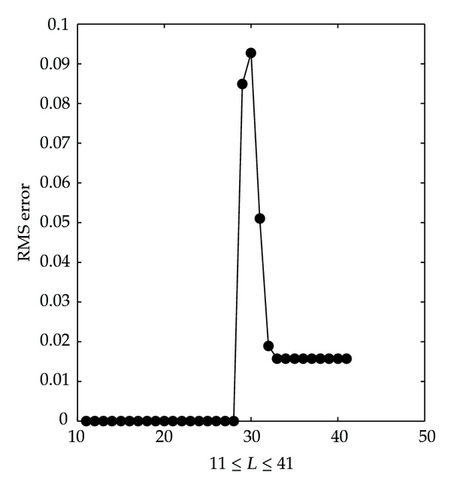
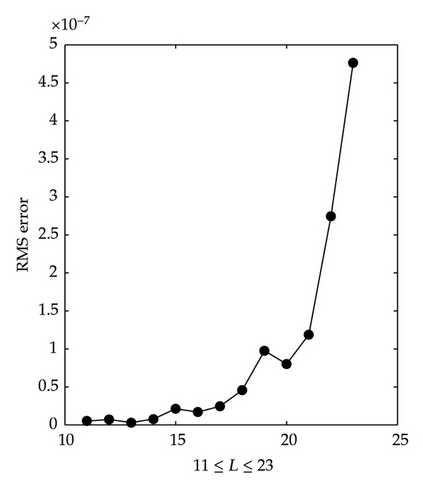
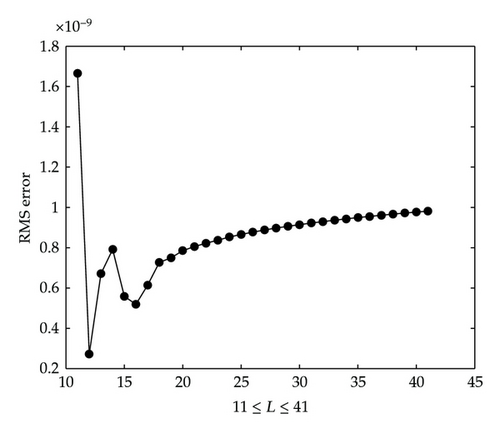
This observation is important for physical problems which require the solution at a high time level. In that case, the number of grid points in time direction should be large and endure oscillations of the solution. Thus, GCL grid points in time are more preferable than ES grid points.

4. Conclusion

The polynomial-based or Fourier expansion-based DQM in space domain and polynomial-based DQM in time domain have been proposed to solve one- and two-dimensional hyperbolic telegraph equations. Differential quadrature method has the capability of producing highly accurate results using considerably small number of grid points, and thus resulting in minimal computational effort. We have used Gauss-Chebyshev-Lobatto grid in space directions which is a nonuniform grid distribution clustering through the end points. For the time direction, equally spaced points may be used for achieving the solution at a specific time level. Considering stability, GCL grids in time direction are more reliable than ES grids when the solution is required at a high time level. The accuracy and efficiency of the results have been demonstrated by root mean square (RMS) and relative errors. The use of FDQ increases the accuracy for one-dimensional telegraph equation especially when the exact solution contains trigonometric functions. For the two-dimensional hyperbolic telegraph equations, the combination of FDQ-PDQ in space and time directions is preferable.

The advantage of the use of DQM both in space and time directions lies in the fact that the solution can be obtained at a required time level by solving one system. There is no need to employ an iteration between the time levels, and large time steps can be used.

    The full text of this article hosted at iucr.org is unavailable due to technical difficulties.