Dynamics of a Transportation Network Model with Homogeneous and Heterogeneous Users

1. Introduction

Network equilibrium models have a long history, both in the transport research literature and in practical studies of scheme assessment, since the notion of user equilibrium (UE) was proposed [1]. At equilibrium, all travelers on the same origin-destination pair experience the same travel cost, while all unused routes have equal or higher travel costs. Wardrop equilibrium has been extended in different senses to address real world needs in transportation planning, analysis, and management, including stochastic user equilibrium (SUE) to allow imperfect information or user perception error in their route choice [2]; dynamic user equilibrium within-day to incorporate the departure time choice in route choice [3, 4].

To model the travelers′ response to exogenous information, the growing interest in day-to-day dynamics has received much study after the original research of Horowitz [5], in which a two-link transportation network is adopted to explain the day-to-day dynamic link and path flow patterns and the stability issue. The evolution over days of travel choices or a learning rule based on the past experience associated with the traffic assignment model are the main methodologies to capture the day-to-day behavior. A comprehensive literature review on the day-to-day dynamics is made by Bie and Lo [6]. In the literature, travelers′ day-to-day route choice adjustment behavior is modeled as either a deterministic dynamic process, such as the simplex gravity flow dynamics [7], the proportional-switch adjustment process [8, 9], the network tatonnement process [10], the projected dynamical system [11], and evolutionary traffic dynamics [12], or a stochastic dynamic process [13, 14]. Yang and Zhang [15] focused on the deterministic dynamic route adjustment process on modeling drivers dynamic route choice adjustment behavior and proved that many commonly used dynamic processes are so-called Rational Behavior Adjustment Process (RBAP) since the aggregated travel cost of the entire network decreases over days except that the path flow becomes stationary and is the user equilibrium path flow. He et al. [16] developed a link-based day-to-day dynamic traffic assignment model to copy with two essential pitfalls of the path-based model, that is, the initial path flow pattern is typically unidentifiable and different initial path flow patterns constituting the same link flow pattern generally give different day-to-day link flow evolutions; the path-based models ignore the interdependence among paths and thus can give very unreasonable results for networks with paths overlapping with each other. The day-to-day route adjustment process provides a useful tool for transportation management. Peeta and Yang [17] demonstrated that providing properly advanced travel information to the road users can result in the social optimal link flow pattern by assuming that the travelers′ day-to-day route adjustment behavior follows the proportional-switch adjustment process. Using the potential games theory, Sandholm [12] proposed an evolutionary implementation mechanism for continuous dynamic route-based pricing policy to ensure the efficient use of the roadway system, while allowing for users to follow any reasonable myopic adjustment process. Apart from the unknown demand or demand function, he assumed that the individual traveler′s day-to-day route choice adjustment process is not known to the planner either.

However, if the road pricing scheme is adopted in the transportation network as Sandholm [12], the day-to-day route adjustment process should incorporate the travelers′ heterogeneous behavior since they value the monetary and time costs in different ways. With this consideration, we assume that all travelers in the transportation network can be classified into several discrete classes, the user in each class is captured by a parameter, value-of-time (VOT) which converts the travel time cost into the equivalent monetary cost [18]. It is easy to understand that the users in different user classes adjust their route choice in different ways according to their VOT values. In this paper, we develop a general model framework to capture the travelers′ day-to-day route choice behavior, which considers the general transportation network with fixed or elastic demand, homogeneous or heterogeneous users. In this study, each traveler is assumed to adjust his/her route choice according to the excess travel cost between the instantaneous experienced travel cost and a certain referred level. The aggregate path flow dynamics induced by this model can be viewed as a natural extension of the so-called rational behavior adjustment process proposed by [15]. We call this path flow dynamics the excess travel cost dynamics, which corresponds to the excess payoff dynamics in evolutionary game [19]. The excess travel cost dynamics serves as a more general framework than the rational behavior adjustment process for modeling the travelers′ dynamic route choice behavior in the transportation network with fixed or elastic demand, homogeneous or heterogeneous users. The Lyapunov function method is commonly used to study the stability of the equilibrium solutions [8, 10]. LaSalle′s theorem addressing system stability over a set of equilibrium solutions rather than an isolated point [20] has been adopted by several researchers to study the stability of dynamic transportation network [6, 17, 21]. In this study, we use LaSalle′s theorem to study the stability of the excess travel cost dynamics.

The paper is organized as follows. Section 2 introduces the definition of the excess travel cost dynamics. The stability issue for the proposed dynamic system is addressed in Section 3. Finally, conclusions are given in Section 4.

2. Day-to-Day Dynamical Route Adjustment Process

3. Stability of the Excess Travel Cost Dynamics

The stability is a central issue for the dynamic system analysis. Peeta and Yang [17] investigated the system stability over a set of desirable states rather than an isolated point, applying LaSalle′s invariant set theorem for the dynamic traffic assignment problem with fixed demand by assuming the proportional-switch adjustment process, given by (2.5). The objective functions of the system optimum and user equilibrium problem are adopted as the Lyapunov functions to conduct the stability analysis, which is physically meaningful. Similar method of constructing Lyapunov function is also used by Jin [21] to examine the system stability of the dynamic traffic assignment problem under OD first-in-first-out violation situation. In this section, in a similar spirit of [17], the system stability of the excess travel cost dynamics proposed in Section 2 is addressed.

A set Π is an invariant set of dynamic system (2.3) if every system trajectory which starts from a point in Π remains in Π for all future time [20]. For instant, any equilibrium point of system (2.3) or, F(f) = 0, as a set is an invariant set. LaSalle′s invariant set theorem is stated as the follows.

The standard LaSalle′s invariant set theorem described above is in general not applicable in the case of discontinuous right-hand side, such as, projected dynamic system [11] and the network tatonnement process [10]. In this case, the generalized invariant set theorem [23] is applicable, only requiring the existence, uniqueness, and continuity of the solution of dynamic system that are guaranteed by assumption (A1). In this study, the standard LaSalle′s invariant set theorem is adopted to investigate the stability issues of dynamic system (2.3).

3.1. Stability Property of the Dynamic System with Homogeneous Users

It is well known that the user equilibrium path flow pattern with elastic (fixed) demand can be identified by solving the following typical elastic (fixed) demand traffic assignment problem

$$ (3.1)

or

$$ (3.2)

Under the assumptions that $$ is strictly decreasing and t_a(·) is strictly increasing, we know that the Wardrop user equilibrium link flow pattern is unique for the case with fixed demand, and the UE demand level is also unique for the case with elastic demand. Denote the set of user equilibrium path flow patterns as

$$ (3.3)

where $$ and $$ are unique UE link flow pattern and corresponding OD demand vector, respectively. It is must be pointed out that, for the case with fixed demand, $$ is the OD demand matrix, and thus, definition (3.3) is suit for both cases with fixed and elastic demand. We first prove that the set (3.3) is an invariant set of system (2.3), that is to say, if any solution with an initial state in set Π will reside in Π for ever, which is depicted in the following lemma.

Lemma 3.2. The set Π, defined by (3.3), is an invariant set of system (2.3), namely, f(0) ∈ Π implies that f(s) ∈ Π, for all s ≥ 0.

Proof. From assumptions (A2)-(A3), we know that F(f) ≠ 0⇒ETC(f)∘F(f) < 0 and, conversely, ETC(f)∘F(f) = 0⇒F(f) = 0, which implies that f is an equilibrium point. It is clear that Π = {f ∈ Ω : ETC(f) = 0} = {f ∈ Ω : F(f) = 0} is an invariant set of system (2.3). The proof is completed.

From Lemma 3.2, we now investigate the stability of system (2.3).

Theorem 3.3. Under assumptions (A1)–(A3), any solution of system (2.3) converges to the invariant set, Π, defined by (3.3), and, thus, the dynamic path flow pattern with any initial state induces the user equilibrium link flow pattern of static traffic assignment problem.

Proof. Consider the following continuously differentiable function (we only consider the case with elastic demand):

$$ (3.4)

where L is the objective function of mathematical programming problem (3.1); q_w, w ∈ W, and v_a, a ∈ A, are functions of path flow pattern f. Let $$, and from Lemma 3.2, the largest invariant set contained in S is Π. In fact, Π = S since S is the solution set of the minimization problem (3.1). Furthermore, note that V(f) > 0 for all f ∈ Ω∖S, and V(f) = 0 for all f ∈ S. Therefore V(f) is a Lyapunov function candidate of system (2.3). Taking derivative of V(f) in day-to-day time, and from assumption (A2), we get, for all f ∈ Ω,

$$ (3.5)

which implies that V(f) is a Lyapunov function of system (2.3). According to the LaSalle′s invariant set theorem, we know that all solutions of system (2.3) converge to Π, which induces the UE link flow pattern. For the case with fixed demand, we can also show that the derivative of V(f) is nonpositive since $$ according to the flow conservation condition. The proof is completed.

The rational behaviour adjustment process proposed by Yang and Zhang [15] is a useful concept frame to model the rational behaviour of the travellers under which the route adjustment process must reduce the aggregate total travel cost of the whole network day by day. However, the definition is suitable only for the case with fixed demand. More generally, the excess travel cost dynamics, or, excess payoff dynamics introduced by Sandholm [19] can incorporate the cases with fixed and elastic demand. Theorem 3.3 depicts that for the excess travel cost dynamics satisfying assumptions (A1)–(A3), any dynamic path flow pattern must move to a certain UE path flow pattern, which induces the UE link flow pattern. Therefore, the set of all UE path flow patterns is a stable invariant set.

Furthermore, for any given link toll pattern, τ = {τ_a, a ∈ A}, the travel cost of path r ∈ R_w between OD pair w ∈ W is the full travel cost (the time cost plus the monetary cost), and the excess travel cost can be defined similarly as the case τ = 0, namely, $$. Then the set of the UE path flow patterns corresponding to the toll vector τ = {τ_a, a ∈ A} is a stable invariant set of system (2.3) or any dynamic path flow pattern must converge to the set. Specially, if the system optimal and fixed link toll pattern, $$ is imposed, where $$ is the SO path flow pattern for fixed- or elastic-demand case, then any dynamic path flow pattern converges to a certain SO path flow pattern, in this case, the invariant set is

$$ (3.6)

where $$ and $$ are unique SO link flow pattern and corresponding OD demand vector, respectively.

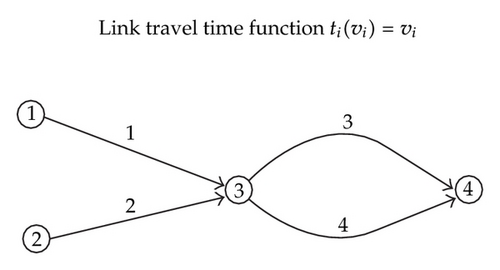
Example 3.4. Consider that the following simple network example, shown in Figure 1, consists of 4 links, 4 nodes, and 2 OD pairs. The OD pairs and the corresponding path are listed in Table 1. Each OD pair has one unit fixed demand. Since all links have the same link travel time function, t_i(v_i) = v_i, it is clear that the user equilibrium path flow pattern is not unique although there is a unique link flow pattern.

Table 1. OD pairs and path sets.

OD pair	Path
1→4	Path 1: {1,3},  f1
q1→4 = 1	Path 3: {1,4},  f3
2→4	Path 2: {2,3}, f2
q2→4 = 1	Path 4: {2,4},  f4

By simple calibration, we know that all nonnegative path flow pattern satisfying condition f₁ + f₂ = 1, f₁ = f₄ and f₂ = f₃ are user equilibrium path flow pattern, which induces the unique link flow pattern, v_i = 1 for all links, i ∈ {1,2, 3,4}. The proportional-switch adjustment process (2.5) is expressed as

$$ (3.7)

where

$$ (3.8)

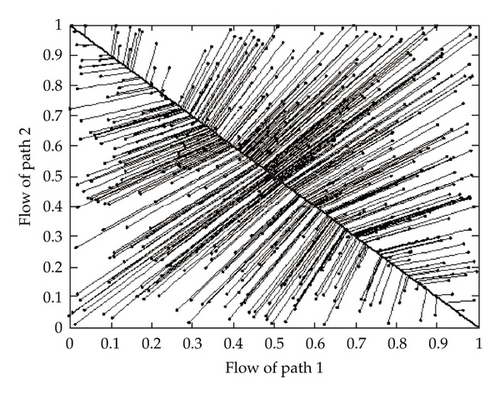
Using MATLAB Simulink, the behavior of the dynamic system (3.7) starting from 500 randomly selected initial states in the all feasible domain is shown in Figure 2. It is clear that, for the path flow dynamic system (3.7), the equilibrium states consist of a set rather than an isolated equilibrium point is an invariant set, and no equilibrium state is stable for path flow pattern in the sense of Lyapunov stability although the link flow is stable.

3.2. Stability Property of the Dynamic System with Heterogeneous Users

We now move to examine the system stability when the travelers are heterogeneous in valuation of travel time. It is well known [24] that the static multiclass traffic assignment problem with fixed demand can be formulated as the following equivalent minimization problem

$$ (3.9)

where the feasible path flow set Ω is given by (2.4). The objective function (3.9) is strictly convex in aggregate link flow v for monotone link travel time function t_a(v_a). Thus, under a given link toll pattern τ, the equilibrium aggregate link flow is unique. However, the class-specific link flow v^M is generally not unique (neither is the UE path flow).

Consider the following continuously differentiable function:

$$ (3.10)

From the proof of Lemma 3.2, we know that $$ is the largest invariant set of multiclass dynamic system (2.3), which is the solution of minimization problem (3.9). Note that V(f) > 0 for all f ∈ Ω, and V(f) = 0 for all f ∈ S. Therefore V(f) is a Lyapunov function candidate of system (2.3). Furthermore, from the assumption (A2′) and the flow conservation $$, we know, for all f ∈ Ω, that

$$ (3.11)

which implies that V(f) is a Lyapunov function of system (2.3). In (3.11), $$ is the excess travel cost of path r ∈ R_w between OD pair w ∈ W for user class m ∈ M defined in Section 2.2. Similar to (3.3), we still denote Π as the set of multiclass user equilibrium path flow patterns as

$$ (3.12)

where $$ and $$ are unique aggregate UE link flow pattern and class-specific OD demand vector, respectively. According to the LaSalle′s invariant set theorem, we know that all solutions of system (2.3) converge to Π, which induces the UE link flow pattern. Therefore, dynamic class-specific path flow pattern with any initial state induces the multiclass user equilibrium link flow pattern by the day-to-day route adjustment process.

Similar analysis can be conducted for the case with elastic demand. In this case, the static multiclass traffic assignment problem with elastic demand can be formulated as the following equivalent minimization problem [24]:

$$ (3.13)

where $$ is the inverse demand function for user class m ∈ M between OD pair w ∈ W. Define the candidate Lyapunov function as

$$ (3.14)

The multiclass UE path flow $$ is the largest invariant set. It is clear that, V(f) > 0 for all f ∈ Ω∖S, and V(f) = 0 for all f ∈ S. Therefore V(f) is a Lyapunov function candidate of system (2.3). By direct calibration, we know, for all f ∈ Ω,

$$ (3.15)

which implies that V(f) is a Lyapunov function of system (2.3). From LaSalle′s invariant set theorem, we have the following stability property for the dynamic system with heterogeneous users.

Theorem 3.5. Under assumptions (A1), (A2′), and (A3), for any given and fixed link toll pattern, any solution of system (2.3) with heterogeneous users converges to a certain user equilibrium path flow pattern, which results in the multiclass user equilibrium link flow pattern.

Although the route adjustment behavior assumption is relaxed to consider the heterogeneity of travelers, that is to say the individual traveler adjusts his/her route choice based on his/her own perception, the multiclass UE link flow pattern is obtained. Theorem 3.5 also provides a method to calculate the multiclass UE link flow pattern.

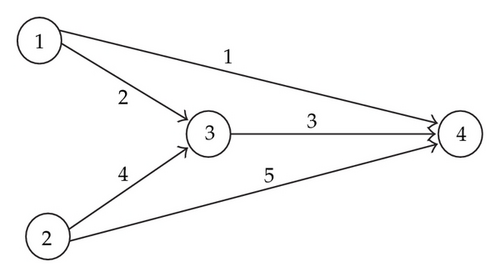
Example 3.6. Consider the network example [18], shown in Figure 3, consisting of 5 links, 4 nodes, and 2 OD pairs. The link cost functions are given by

$$ (3.16)

There are two classes of travelers with different values of time, class 1 consists of travelers with a lower value of time of β₁ = 1.0 (Yuan/min) and class 2 consists of travelers with a higher value of time of β₂ = 2.0 (Yuan/min). The OD pairs and the corresponding path are listed in Table 2. Let $$ denote the flow of path r ∈ {1,2, 3,4} between OD pair w ∈ {1,2}, with user class m ∈ {1,2}. The demand for each user class between each OD pair is $$, $$, $$, and $$. Given the link toll pattern of τ₁ = τ₃ = τ₄ = 0, and τ₂ = τ₅ = 10 Yuan, which results in the static multiclass user equilibrium link flow pattern, v₁ = 10, v₂ = 10, v₃ = 20, v₄ = 10 and v₅ = 20. Here we still adopt the proportional-switch adjustment process (PSAP) to model the multiclass path flow dynamics. From the flow conservation, we only consider four free variables, $$, $$, $$, and $$. The PSAP (2.5) is expressed as:

$$ (3.17)

where

$$ (3.18)

and $$ and $$ are the total travel time and toll of path r ∈ R_w between OD pair w ∈ {1,2}, respectively. Using MATLAB Simulink, the path flow pattern of the dynamic system (2.5) starting randomly from selected initial state converges to the unique solution, in which, $$, $$, $$ and $$. Denote $$ as the class-specific average travel cost in time unit between OD pair w ∈ {1,2}, such as, for m ∈ {1,2},

$$ (3.19)

The day-to-day aggregate excess travel cost in time unit can be calculated as

$$ (3.20)

which approaches zero. The behavior of the dynamic system (3.17), starting from 200 randomly selected initial states in all the feasible domain, is shown in Figures 4 and 5. Observed from the two figures for the multiclass case, the state trajectories become chaotic since the individual traveler adjusts his/her route choice based on his/her own value of time. However, the trajectories with any initial states solution for the path flow dynamic system (3.17) converge to the UE path flow pattern.

Table 2. OD pairs and path sets.

OD pair	Path
1→4	Path 1: {1}
q1	Path 3: {2,3}
2→4	Path 2: {4,3}
q2	Path 4: {5}

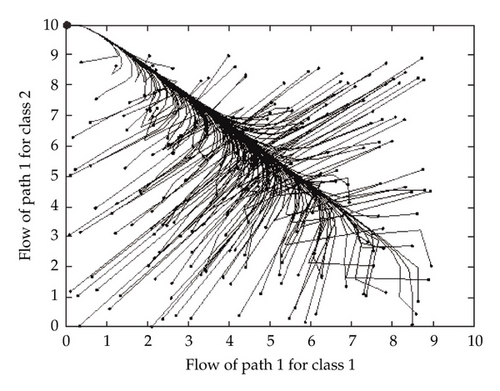
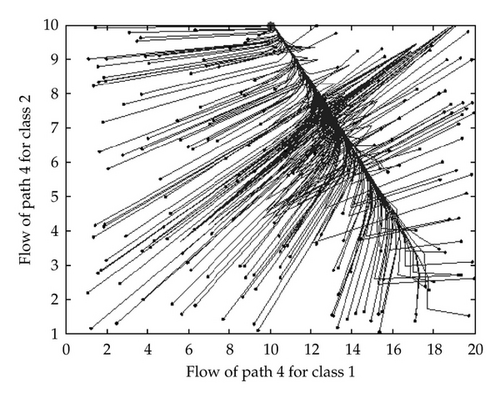
4. Conclusion

We presented an excess travel cost dynamics to model travelers′ route choice behavior in a transportation network with fixed or elastic demand and homogeneous or heterogeneous users. The excess travel cost dynamics is a natural extension of the rational behavior adjustment process proposed by Yang and Zhang [15], which corresponds to the excess payoff dynamics in evolutionary game [19]. The excess travel cost dynamics serves as a more general framework than the rational behavior adjustment process for modeling the travelers′ dynamic route choice behavior in the transportation network with fixed or elastic demand, homogeneous or heterogeneous users. LaSalle′s theorem is adopted to study the dynamic system stability. We proved that the trajectories of the excess travel cost dynamics with any initial state converge to the user equilibrium link flow pattern in various scenarios (fixed or elastic demand, homogeneous or heterogeneous users).

It is an interesting challenge to design the system optimum pricing scheme in a transportation network by taking into account both the hidden actions of travelers′ day-to-day route choice adjustment and the true but unknown demands, specially, with heterogeneous users. Another research direction is to model the heterogeneous behavior of the travelers on their perceived travel cost except the way valuing the monetary and time costs, which requires a stochastic dynamic route choice process incorporating the user heterogeneity.