Step Soliton Generalized Solutions of the Shallow Water Equations
Abstract
Generalized solutions of the shallow water equations are obtained. One studies the particular case of a generalized soliton function passing by a variable bottom. We consider a case of discontinuity in bottom depth. We assume that the surface elevation is given by a step soliton which is defined using generalized solutions (Colombeau 1993). Finally, a system of functional equations is obtained where the amplitudes and celerity of wave are the unknown parameters. Numerical results are presented showing that the generalized solution produces good results having physical sense.
1. Introduction
The classical nonlinear shallow water equations were derived in [1]. There exist several works devoted to the applications, validations, or numerical solutions of these equations [2–5]. These equations provide a significant improvement over linear wave theory to describe the wave-breaking process [6].
Shallow water equations have been submitted to numerous improvements to include several physical effects. In such sense, several dispersive extensions were developed. The inclusion of dispersive effects resulted in a big family of the so-called Boussinesq-type equations [7–10]. Many other families of dispersive wave equations have been proposed as well [11–13]. Other studies attempt to include the effect of different types of bottom shape [4, 14–19]. Also in [20, 21], the mild slope hypothesis is not required, and rapidly varying topographies was also considered. In these studies, the asymptotical expansion method was used. In [22] was included different geometry bathymetric by improving the shallow water equations by using variational principles.
However, there are a few studies which attempt to include the discontinuous or not differentiable bottom effect into shallow water equations [23–25]. One reason is that in its deduction procedure, assume certain restrictions on bottom type function as differentiability. In [3], a numerical method to studding the discontinuous bottom was used.
In this paper, we relaxedly completed this hypothesis allowing that the bottom function must be not differentiable by using the Colombeau algebra [26, 27] studying the shallow water equations with a discontinuous bottom. This algebra comes being used in several applications of the physics fields studying nonlinear partial differential equation. In this theory, the previous solutions are still valid because of the natural embedding of the distribution in the sense of Schwartz in this algebra. In particular the smooth functions are embedded as a constant sequence. However, this theory is specially useful when the product distribution is not allowed or when a formalism of continuous function is not more valid. Details of Colombeau algebra in the applications to hydrodynamics of can be found in [28].
The method presented in this paper is general, and it can be used for a wide class of nonlinear dispersive wave equations such as Boussinesq-like system of equations. In order to try the possibilities of this theory, we consider the equation deduced in [6] with the principles that the equality p − po = ρg(ho + η) holds; here, p is the pressure, ho is the depth, ρ is the density of the water, and η is the surface elevation. This equality for the discontinuous bottom case is not more valid in the classical sense. So, we embedded the classical distribution in the generalized function where the nonlinear operations are allowed. Also, we consider the dispersive equations deduced in [8] which is valid to variable smooth bottom. Similar formulas obtained in this paper were obtained in [29] by using the method of the lines.
To study the nonlinear and bottom irregularities effects, we consider the shallow water equations to simulate a generalized soliton passing by discontinuity in the bottom. The idea of taking a soliton to describe a traveling wave and singular solution as a soliton was developed by several works [30–35]. In [36], a generalized solution in the frame of Colombeau’s generalized functions was obtained. Solitons are used in coastal engineering to describe waves approximating to the coast with the presence of a vertical structure [37–41]. The evolution of a solitary wave at an abrupt junction was measured and discussed by [42] in detail. There exist a number of physical reasons to suppose that the propagation of a soliton wave over a discontinuity point in the bottom preserves the shape and the structure of an initial wave [43].
The starting point, that the bottom has a discontinuity, constitutes a generalization of submerged structure or coral reef representation. This situation is equivalent, in practical engineering, to the presence of a vertical hard structure that in some cases breaks the wave propagation. As a wave propagates over the structure, part of the wave energy is reflected back to the open ocean, part of the energy is transmitted to the coast, and part of the energy is converted to turbulence and further dissipated in the vicinity of the structures [39, 44]. These processes we approximated by using two generalized solitons traveling in opposite direction.
In this paper, we obtain generalized solutions of the shallow water equations in the one-dimensional case. The approximate solution is obtained as a singular solution. We suppose that in microscopic sense, when a wave crosses the discontinuity bottom point, one part continues its propagation to the shore, preserving the initial structure, while another part is reflected. We use a generalized soliton function which has macroscopic aspect in sense of Colombeau [27], that is, for a given τ1, for τ < −τ1, for −τ1 < τ < τ1 and for τ > τ1. We obtain a nice procedure that reduces the problem of finding a solution of nonlinear partial differential equation to the one of solving a system of algebraic equations. Since this attempt used this theory to obtain practical formulas, we prove that in the limit, the Step generalized solution agreement reasonably with previous classical solutions. Moreover, we prove that by fixing some parameter that appears in this theory, some nonlinear and dispersive effects are reproduced well.
This paper begins with a description of the Colombeau algebra. Some useful proposition including different product of generalized function was established to simplify some nonlinear operations. After that, generalized solutions are obtained for the flat bottom for two types of shallow water equations. In both cases the generalized solution is compared with previous formulas. Finally, we propose a method to obtain the generalized solution in the discontinuous bottom case. The accuracy of the numerical scheme for solving the shallow water equations was verified by comparing the numerical results with the theoretical solutions obtained by [45] and experimental data obtained in [46].
2. Colombeau Algebra
In this paper, we use a generalized solution deduced from the algebra of Colombeau [27, 47]. Such solution permits to construct a singular solution of the system of conservation law that preserves its structures and initial shape. These functions appear in the multiplication of distributions theory when nonlinear differential equations are studied.
Es(Ω) and EM(Ω) are algebras, and N(Ω) is an ideal of Es(Ω).
Definition 2.1. The simplified algebra of generalized functions is the quotient space ℑs(Ω) = Es(Ω)/N(Ω).
The elements G of ℑs(Ω) are denoted by G = R1(ϵ, x) + N(Ω). Distribution of compact support on ℝ can be embedded on ℑs(ℝ) by convolution with a mollifier ρϵ, defined as follows: let ρ ∈ S(ℝ) (Schwartz’s space) with the properties ∫ ρ(x)dx = 1, ∫ xαρ(x)dx = 0, for all α ∈ N2, | α | > 1, then we set ρϵ(x): = (1/ϵ) 2ρ(x/ϵ). Then the generalized function ∫ xαρɛ(x − y)w(x)dx + N(Ω) belongs to ℑs(ℝ) [28].
ℑs(Ω) is clearly an algebra with the usual pointwise operations of addition, inner multiplication, and exterior multiplication by scalars. In this algebra, there are two equalities, one strong ( = ) and one weak (~). The strong one is the classical algebraic equality. The weak one is called association and is denoted by the symbol ~; in other words, two simplified generalized functions are equal if the difference of two of their representatives belongs to the ideal N(Ω). Also, whereas multiplication is compatible with equality in ℑs(Ω), it is not compatible with association. Therefore, the distinction between ( = ) and (~) automatically ensures that the physically correct solution is selected, a distinction that can be made in analytical as well as in numerical calculations by using a suitable algorithm [27, 28].
Definition 2.2. Two generalized functions G1, G2 ∈ ℑs(Ω) are associated, G1 ~ G2, if there exists representatives R1, R2 ∈ Es(Ω) of G1, G2 respectively, such that: for all ψ ∈ D(ℝ), ∫ℝ (R1(ϵ, x) − R2(ϵ, x))ψ(x)dx → 0 when ϵ → 0.
In the interpretation of the generalized solution, we use that two different generalized functions associated with the same distribution differ by an infinitesimal.
It is well known from the classical asymptotical method that the several solutions depend on an infinitesimal ϵ. For example, in [6, page 470], the solution of the Korteweg de Vries is given in linear limit as ςϵ = λcos (ϵ(x − ct)), whereas in the solitary waves limit as ςϵ = λ sech (ϵ(x − ct)). In [36], similar solutions are obtained in the sense of Colombeau. These functions show that even in the classical sense, the solution is given by a family of functions. The idea to look for a generalized solution in the sense of Colombeau means to seek a solution like a family that depend of one infinitesimal, but this extension must guarantee that they keep valid the association by differentiation and nonlinear operations between them.
- (i)
C∞(Ω) ⊂ ℑs(Ω),
- (ii)
let ρ ∈ D(ℝ) be a C∞(ℝ) function such that ∫ℝ ρ(x)dx = 1. Then the class of R1(ϵ, x) = (1/ϵ)ρ(x/ϵ) is an element of ℑs(Ω) associated with the Dirac delta function, that is, for all ψ ∈ D(ℝ), ∫ℝ R1(ϵ, x)ψ(x)dx → ψ(0), when ϵ → 0, where D(ℝ) denotes the space of the infinitely smooth functions on ℝ with compact support.
- (iii)
it is possible to define the integral of generalized functions in the following way: let G ∈ ℑs(ℝ) and R1 ∈ Es(ℝ) a representative. The application R2 : (ϵ, x)∈(0,1) × ℝ → ℝ is defined by
(2.2)
The association ~ is stable by differentiation but not by multiplication, that is, if G1, G2, G ∈ ℑs(ℝ), and G1 ~ G2 then , but GG1 and GG2 are not necessarily associated.
Definition 2.3. A generalized function H ∈ ℑs(ℝ) is called a Heaviside generalized function if it has representative R ∈ Es(ℝ) such that there exists a sequence of real numbers A(ϵ) > 0, A(ϵ) → 0, when ϵ → 0 such that
- (i)
R(ϵ, x) = 0, for all ϵ > 0, and x < −A(ϵ),
- (ii)
R(ϵ, x) = 1, for all ϵ > 0, and x > A(ϵ),
- (iii)
sup | R(ϵ, x)|<+∞, ϵ > 0, and x ∈ ℝ.
The Heaviside generalized functions are associated between them. Moreover, Hn ~ H for n ∈ ℕ, n > 0.
Definition 2.4. A generalized function δ ∈ ℑs(ℝ) is called Dirac generalized function if it has a representative R ∈ Es(ℝ) such that there exists a sequence A(ϵ) > 0, A(ϵ) → 0, when ϵ → 0 such that
- (i)
R(ϵ, x) = 0, for all ϵ > 0, and |x | > A(ϵ),
- (ii)
∫ℝ R(ϵ, x)dx = 1, for all ϵ > 0,
- (iii)
∫ℝ | R(ϵ, x) | dx < C, for all ϵ > 0, where C is a constant independent of ϵ.
It is possible to check that the relation H′ ~ δ holds between Heaviside and Dirac generalized functions. Moreover, for a reasonable Heaviside and Dirac generalized function, there exists a constant M such that Hδ ~ Mδ.
Definition 2.5. For a given τ1 > 0, a generalized function is called a step soliton generalized function if it has a representative R ∈ Es(ℝ) defined by
- (i)
R(ϵ, x) = R1(ϵ, x − τ1) − R2(ϵ, x + τ1),
For instance, R1(ϵ, x) = 0 if x + τ1 ≤ 0, R1(ϵ, x) = 1 if x + τ1 ≥ ɛ, and R1(ϵ, x) > 0 if 0 < x + τ1ɛ (see Figure 1(a)). Besides, R1(ϵ, x) = 0 if x − τ1 ≤ 0, R1(ϵ, x) = 1 if x − τ1 ≥ ɛ, and R1(ϵ, x) > 0 if 0 < x − τ1ɛ (see Figure 1(b)). In Figure 1(c), the graph of R1(ϵ, x + τ1) − R1(ϵ, x − τ1) is shown.
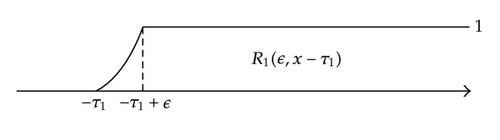
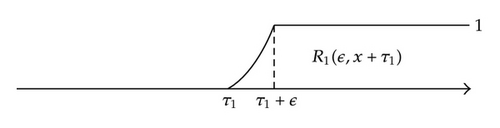
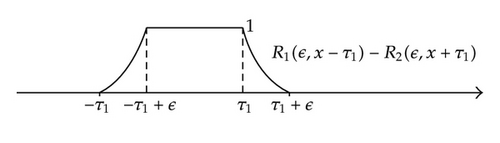
From Definition 2.5, we obtain that the equality holds. Moreover, the macroscopic aspect of the step generalized function is not necessarily symmetric (see Figure 1). A lesson from this application is that by assuming that physically relevant distributions such as Heaviside H and Dirac δ generalized function are elements of ℑs(ℝ); one gets a picture that is much closer to reality than if they are restricted to classical sense. This fact can be exploited in mathematical and physical modeling. We can verify that the step generalized soliton has one as the maximum value of its representatives. Thus, it is possible to verify that the generalized function has λ as the maximum values.
Definition 2.6. A generalized function δ1 ∈ ℑs(ℝ) is called a microscopic soliton generalized function if it has a representative R ∈ Es(ℝ) defined by
- (i)
R(ϵ, x) = 1 − R1(ϵ, x) − R1(ϵ, −x),
3. Some Useful Lemmas
Reviewing cases of the product of two step generalized functions, the product with function Heaviside generalized function, and the product derivatives of step generalized functions, as well as products with the microscopic generalized functions, it should be noted that the depth with a discontinuity is closer to the combination of the Heaviside generalized functions. In the calculations with generalized function on the shallow water equations arise the derivatives of Heaviside generalized functions which are reasonably approximated by delta generalized function. In short, in the upcoming paragraph, we show those useful lemmas of the product of generalized functions that allow to simplify the calculations and obtain in this way algebraic equations.
To prove the main results of this paper these lemmas of generalized functions are needed. Such lemmas consist in simplifing association between the product of several generalized functions that appears in the algebras of substitution of the proposal solution in the shallow water equations. Let us prove the following.
Lemma 3.1. Given τ1 > 0, let it be denoted by and H the step and Heaviside generalized functions respectively. Then the following relations hold:
Proof. We have that . From this there exists constant M such that for t > 0, c > 0, and ct − τ1 > 0, we have δ(x − ct + τ1)H(x) ~ Mδ(x − ct + τ1) and δ(x − ct − τ1)H(x) ~ Mδ(x − ct − τ1), then (3.1) holds.
It possible to check that for t > 0, c > 0, and −ct + τ1 < 0, (3.2) holds.
Lemma 3.2. Given τ1 > 0, let it be denoted by the step generalized functions. Then the following relations hold:
Proof. We have that , δ(x)H(x − ct + τ1) ~ 0, and δ(x)H(x − ct + τ1) ~ 0 for t > 0 and c > 0; thus, (3.3) holds. Analogously, it is possible to verify that (3.4) holds.
The following propositions are useful.
Lemma 3.3. Given τ1 > 0, c > 0, and t such that t > τ1/c, let it be denoted by and the step soliton and its derivative generalized functions, respectively. Then the following relations hold:
- (i)
,
- (ii)
,
- (iii)
.
Proof. We prove here that (ii) the others are similar. We have that and , where δ and H are the Dirac and Heaviside generalized function. It is possible to check that for t > τ1/c, the delta soliton of the stays in the null part of step soliton , so (ii) holds.
Lemma 3.4. Given τ1 > 0, c > 0, and t such that t > τ1/c, let it be denoted by and δ1 the step soliton and microscopic generalized functions, respectively. Then the following relations hold:
- (i)
,
- (ii)
.
4. The Flat Bottom Case
4.1. Nonlinear Effect
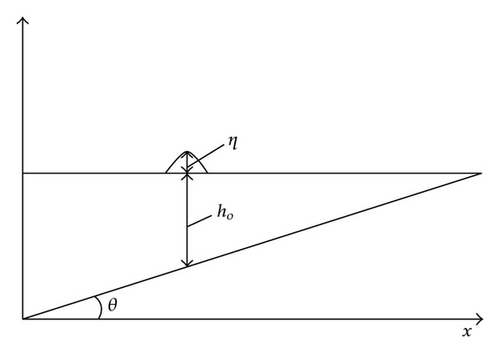
Assumption 4.1. Particles in a vertical plane at any instant always remain in a vertical plane, that is, the streamwise velocity is uniform over the vertical. Each vertical plane always contains the same particles; hence, the integration volume is moving with the fluid.
With the previous assumption, we have chosen a material reference frame to describe the motion of the soliton in the fluid.
For a given τ1, let us denote by the derivative of the step soliton generalized function . We interpret (4.1) and (4.2) in the sense of association, that is, we seek the analog of classical weak solutions (see [26, 27, 47, 50]). We are going to seek solutions of the system (4.1) and (4.2) in the form of where is a step soliton generalized function. The following theorem holds.
Theorem 4.2. It is assumed that solitons of the system (4.1) and (4.2) are given by
Proof. Using that h = ho + η and substituting (4.3a) and (4.3b) in (4.1) with ξ = x − X(t), we obtain
Remark 4.3. The choice of the particle velocity u as a product by the step generalized function (see (4.3b)) like the free surface stays in concordance which linear wave theory, see as an example [45, 51].
Remark 4.4. Taking off the amplitude wave λ from (4.4b) and substituting in (4.4a) we obtain
Theorem 4.2 has an immediate practical sense: the trajectory of the singularity is linear for the case of planar bottom with the system of (4.1) and (4.2).
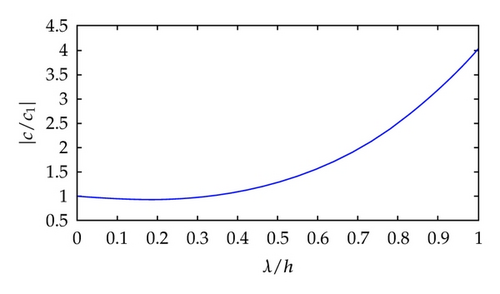
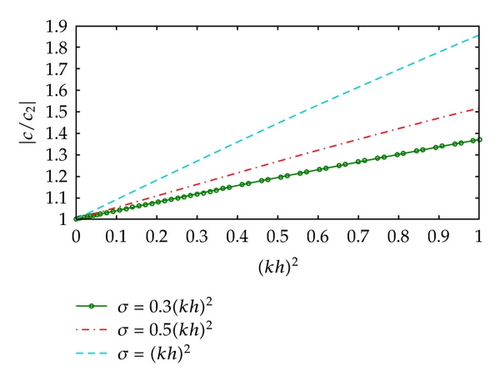
4.2. Nonlinear and Dispersive Effects
The following theorem holds.
Theorem 4.5. It is assumed that solitons of the system (4.20) are given by
Proof. Since the proof is similar to Theorem 4.2, we present a summary here. The idea of the proof consists in substituting the generalized function (4.21) in the system (4.20). By using the relations and , ξ = kx − ωt and after several operations, we obtain
Remark 4.6. Taking ν1 = ν2 = 0 in (4.25) and (4.26), that is, neglecting the dispersive effects, it is possible to verify that (4.22) and (4.23) are the same as that (4.4a) and (4.4b) in Theorem 4.2 (the nonlinear effect alone), which indicates that the calculations are consistent.
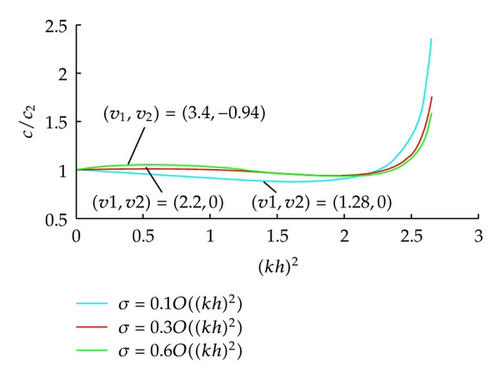
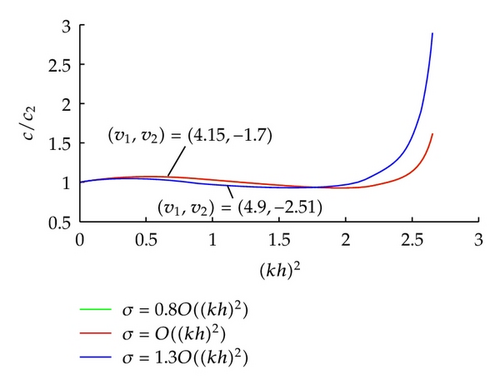
5. A Discontinuity Bottom Case
In this section, we studied the case in which a soliton crosses a bottom discontinuity (see Figure 5). Seeking the solution of shallow water equation requires some useful lemmas that were proved in Section 3. These propositions contain the key results of the product of generalized functions that appear in the algebraic operations when generalized solution is searched.
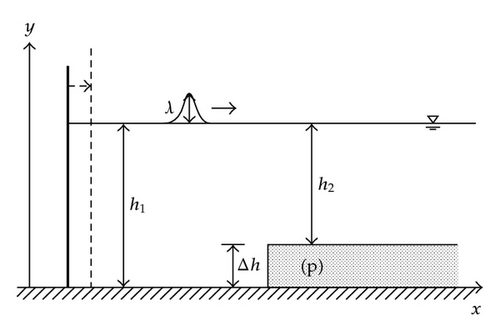
5.1. Generalized Solution
5.1.1. A Case of Single Soliton
Theorem 5.1. It is assumed that solitons of the system (5.3) and (5.4) are given by
Proof. Substituting (5.6) and (5.5) in (5.3) with ξ = x − X(t), we obtain
Remark 5.2. Theorem 5.1 indicates that the trajectory of the singularity of one soliton that passes by the discontinuity point in the bottom consist in a cone. Moreover, the velocity of the soliton is constant and different in both sides of the jump. This suggests from the physical point of view that happened, a rectification of the soliton and velocity only depends on the depth.
5.1.2. A Case of Two Solitons
Now, we obtain a solution of shallow water equation as two solitons which we assume are the propagate soliton, and reflected by the jump. Using the heuristic considerations despite in Remark 5.2, we assume that the velocity of the solitons is constant.
Theorem 5.3. For given τ1 > 0, let it be assumed that a generalized solution of (5.3) and (5.4) is given by (5.13) with bottom depth given in (5.5). Assuming that the amplitudes λ and uo are known, then the wave velocities c1 and c2, the amplitude of particle velocity uo2, and the amplitude λ2 of reflected wave satisfy on t > min {τ1/c1, τ1/c2} the following algebraic equations:
Proof. Denote that by ξ1 = x − c1t and ξ2 = x + c2t, we have
Remark 5.4. Although Theorem 5.3 was obtained for a discontinuity in the bottom, it is not difficult to generalize this result for any type of bottom. To do so, any geometric of the bottom can be approximated by step functions, and then theorem can be used locally.
Remark 5.5. In Theorem 5.3, we assume that t > min {τ1/c1, τ1/c2}. If we relax this hypothesis, that is, to obtain the generalized solution on 0 < t < min {τ1/c1, τ1/c2}, we have that, following relations hold:
6. Numerical Calculation of the Generalized Solution
In this section, we show a numerical procedure to find the unknown parameters λ2 and uo2 which are solution of the system of (5.15)–(5.18). In practical terms to determine those parameters means to calculate the amplitude of the step Soliton when it passes through a point of discontinuity in the bottom. The method consists in reducing the set of four equations to two by eliminating the unknowns c1 and c2. The following lemma holds.
Lemma 6.1. Let it be assumed that a generalized solutions of (5.3) and (5.4) is given by (5.13) with bottom depth given in (5.5). Assuming that λ and uo are known, then the amplitude of particle velocity uo2 and the amplitude λ2 of the reflected wave satisfy
Proof. Equation (6.1) follows from (5.18) minus (5.16). Equation (6.2) follows from (5.17) minus (5.15).
7. Numerical Examples
In this section, we show that the generalized solutions with physical sense can be obtained. To do so, the constant M in the system of (5.15)–(5.18) can be adjusted such that generalized solutions represent appropriately the theoretical and experimental data.
The initial values of quasi-Newton method for solving (6.1)-(6.2) are taken by using the formula for planar bottom case; that is, assuming the wave celerity is known from (4.4a) and (4.4b), we obtain . It is possible to check that the positive root of the above equation produces a wave amplitude with reasonable value.
We take the example described in [40] which considered the discontinuity bottom as h1 = 80 cm, h2 = 40 cm, and the initial amplitude λ = 4 cm. The theoretical result for this case using the formula (7.1) is compared with numerical solution of the system of (5.15)–(5.18). To approximate the theoretical solution, we present the generalized solution assuming that the constant M in system of (6.1)-(6.2) depends on x/h2, that is, M = M(x/h2). This assumption enables us to show that the solution of (5.15)–(5.18) can reproduce well several amplitude step soliton values above the break point. We seek the values of the M(x/h2) that better adjusted the theoretical amplitude in (7.1) (see Figure 6). To do so, we use the solver fmincon.m in MATLAB 7.0. In Figure 6 is shows the theoretical and predicted step soliton amplitude when pass on a discontinuous depth point (x = 0).

In [46] was performed experiments to investigate the harmonic generation as periodic waves propagate over a submerged porous breakwater. Their experimental data will be used to test the validation of the present model equations for the wave and discontinuous bottom point interaction. We check that the generalized solution can reproduce well this experimental values.
Although we have been adjusted the method well to both theoretic and experimental data, this result constitutes a first approximation of application of Colombeau’s algebra, because we consider as a constant in time and space the amplitude of step soliton generalized function. Also, we do not consider here the friction effect and the time dependency amplitude wave. An other facility is that the parameter M that appears in (5.15) can be estimated from several experimental runs looking for any regularity.
8. Conclusion
In this paper generalized solutions in the sense of Colombeau of Shallow water equations are obtained. This solution is consistent with numerical and theoretical results of a soliton passing over a flat or discontinuity bottom geometries. The method developed in this paper reduces the partial differential equation to determine the zeros of a functional equation. This procedure also will allow us to study a propagation of several types of singularities on several bottom geometries.
Acknowledgments
The authors are grateful to Herminia Serrano Mendez for their collaboration. They thank the oceanographist Alina Rita Gutierrez Delgado for helpful discussions and review of the paper. They are also very pleased of the reviewers who helped them improve the paper. The authors appreciate the help of Dan Marchesin and special thanks for Iucinara Braga. They also thank IMPA, Brazil and the University of Université des Antilles et de la Guyane.




