Discrete Dynamics in Nature and Society
Volume 2012, Issue 1 894207
Research Article
Open Access

Spatial Cluster Analysis by the Adleman-Lipton DNA Computing Model and Flexible Grids

Xiyu Liu, 

Corresponding Author

Xiyu Liu

School of Management Science and Engineering, Shandong Normal University, 250014 Jinan, China sdnu.edu.cn

Search for more papers by this author
Laisheng Xiang, 

Laisheng Xiang

School of Management Science and Engineering, Shandong Normal University, 250014 Jinan, China sdnu.edu.cn

Search for more papers by this author
Xin Wang, 

Xin Wang

School of Management Science and Engineering, Shandong Normal University, 250014 Jinan, China sdnu.edu.cn

Search for more papers by this author
First published: 23 April 2012
https://doi.org/10.1155/2012/894207
Citations: 8
Academic Editor: Bo Yang

Abstract

Spatial cluster analysis is an important data-mining task. Typical techniques include CLARANS, density- and gravity-based clustering, and other algorithms based on traditional von Neumann’s computing architecture. The purpose of this paper is to propose a technique for spatial cluster analysis based on DNA computing and a grid technique. We will adopt the Adleman-Lipton model and then design a flexible grid algorithm. Examples are given to show the effect of the algorithm. The new clustering technique provides an alternative for traditional cluster analysis.

1. Introduction

Deoxyribonucleic acid computing, or DNA computing in short, has attracted strong interests and wide focus recently. It is inspired by the similarity between the way DNA stores and manipulates information with traditional Turing machine. Although DNA computing is in a sense similar to evolutionary computing, but the significant difference between them lies in the computing medium, biomolecules rather than transistor chips. It is this difference that makes DNA computing a promising field with ultimate goal of making DNA computers [1].

The essential work to reveal the ability of DNA in computing is by Adleman’s experiment (Adleman [2]), which demonstrated that the tools of laboratory molecular biology could be used to solve computation problems. Adleman also proves the huge information storage capacity of DNA which is contained in the sequence of nucleotide bases that hydrogen bonds in a complementary fashion to form double-stranded molecules from single-stranded oligonucleotides. Adleman’s work was later generalized by Lipton [3] to the satisfiability problem. Based on Adleman and Lipton’s research, a number of applications of DNA computing in solving combinatorially complex problems such as factorization, graph theory, control, and nanostructures have emerged [1]. There appeared also theoretical studies including DNA computers which are programmable, autonomous computing machines with hardware in biological molecules mode, see [4–7] for references.

Adleman and Lipton’s original works include a basic computing model, often referred to as the Adleman-Lipton model. Later generalizations include the sticker model, the splicing model, and the insertion deletion model [1]. However, most applications in this area are restricted to problems of combinatory types due to searching nature of DNA computing. It is a challenge how to design applications of optimization types.

Spatial cluster analysis is a traditional problem in knowledge discovery from databases [8]. It has wide applications since increasingly large amounts of data obtained from satellite images, X-ray crystallography, or other automatic equipment are stored in spatial databases. The most classical spatial clustering technique is due to Ng and Han [9] who developed a variant PAM algorithm called CLARANS, while new techniques are proposed continuously in the literature aiming to reduce the time complexity, or to fit for more complicated cluster shapes.

For example, Bouguila [10] proposed some model-based methods for unsupervised discrete feature selection. Wang et al. [11] developed techniques to detect clusters with irregular boundaries by a minimum spanning tree-based clustering algorithms. By using an efficient implementation of the cut and the cycle property of the minimum spanning trees, they obtain a performance better than O(N2). In another paper, Wang and Huang [12] developed a new density-based clustering framework by a level set approach. By a valley seeking method data points are grouped into corresponding clusters.

Although DNA computing and cluster analysis receive much attention and rapid development, there have appeared rare combination of these two important research areas. Up to the authors knowledge, the combination of DNA computing and cluster analysis is found in a few researches such as Bakar et al. [7].

Inspired by the research of Bakar et al. [7], this paper focuses on the joint study of DNA computing with cluster analysis. We propose a new grid-based clustering technique which can be solved by DNA computing. Different with other researches, this can reduce the searching space significantly. Finally we present two examples to show the details of our technique.

2. DNA Computing and Operations

2.1. DNA Structures

Macromolecules of nucleic acids are composed of nucleotide building blocks. In DNA, the nucleotides are the purines adenine (A), guanine (G), the pyrimidines thymine (T), and cytosine (C). Single-stranded DNA molecules, or oligonucleotides, are formed by connecting the nucleotides together with phosphodiester bonds. The single strands of DNA can form a double-stranded molecule when the nucleotides hydrogen bonds to their Watson-Crick complements, and (Figure 1).

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
A double-stranded DNA structure diagram.

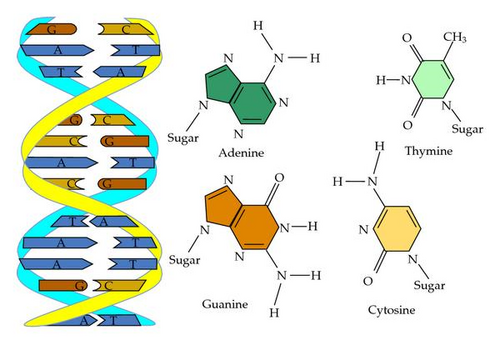
DNA stores information in nucleic acid and manipulates information via enzymes and interactions. A strand of DNA is encoded with four bases represented by the letters A, T, C, and G. Each strand has a 3′- and a 5′-end, and hence any single strand has a natural orientation. The cutting of certain strands of a DNA molecule is performed by the restriction enzymes. These enzymes catalyse the cutting operations at very specific DNA base sequences which are called recognition sites. Figure 2(a) shows a DNA molecule in which its four nucleotides in the left end and five in the right end are not paired with nucleotides from the opposite strand caused by cutting, or some other operations. In this case, the molecule is called to have sticky ends.

Details are in the caption following the image
Figure 2 (a)
Open in figure viewerPowerPoint
DNA molecules with sticky ends.
Details are in the caption following the image
Figure 2 (b)
Open in figure viewerPowerPoint
DNA molecules with sticky ends.
Details are in the caption following the image
Figure 2 (c)
Open in figure viewerPowerPoint
DNA molecules with sticky ends.
Here is an example which illustrates the process by the enzyme EcoRI as shown in Figure 2(b) where N represents some other arbitrary deoxyribonucleotide. EcoRI acts only at the six-term sequences which are exactly like the form
(2.1)

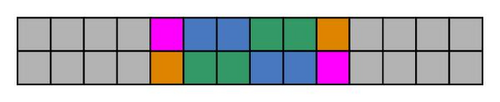
The effect is to cut the molecule into two pieces as shown in Figure 2(c).

There are over 100 different restriction enzymes, each of which cuts at its specific recognition site. A restriction enzyme cuts DNA into pieces with sticky ends. On the other hand, sticky ends will match and attach to other sticky ends of any other DNA that has been cut with the same enzyme. DNA ligase joins the matching sticky ends of the DNA pieces from different sources that have been cut by the same restriction enzyme.

2.2. DNA-Computing Models

There are several types of DNA-computing models among which the Adleman-Lipton model is the most traditional one. This model focuses on the hybridization between different DNA molecules as a basic step of computations. According to Adleman and Lipton’s original works [2, 3], this traditional DNA-computing strategy is based on enumerating all candidate solutions, and then using some selection process to choose the correct DNA. This technique requires that the size of the initial data pool increases exponentially with the number of variables in the calculation.

Apart from the Adleman-Lipton model, other DNA computing models appeared such as the sticker model, the splicing model. The Sticker model is based on a coding scheme called DNA complex. A DNA complex is a partially double DNA strand. Usually a double piece represents a bit with value one while a single-strand represents zero. Hence each complex is constructed by two single stranded DNA molecules referred to as memory strands and sticker strands. A memory strand contains n nonoverlapping substrands each of which is m bases long. Each sticker strand is m bases long and is complementary to exactly one of the n substrands in a memory strand.

The second model is the splicing model proposed by Tom [6] based on formal language theory. A splicing system S = (A, L, B, C) consists of a finite alphabet A, a finite set I of initial strings in A* (language over A), and finite sets B and C of triples (c, x, d) with c, d, x ∈ A*. Each such triple in B or C is called a pattern. For each such triple the string cxd is called a site, and the string x is called a crossing. Patterns in B are called left patterns, and patterns in C are called right patterns. The language L = L(S) generated by S consists of the strings in I and all strings that can be obtained by adjoining to Lucxfq and pexdv whenever ucsdv and pexfq are in L and (c, x, d) and (e, x, f) are patterns of the same hand. A language L is a splicing language if there exists a splicing system S for which L = L(S).

The next model is the k-armed model which is based on some more complicated molecule structures which have three-dimensional DNA architecture. In [13] the authors pointed out that it is natural to use the armed model to represent SAT problem in terms of contact network framework, and they gave theoretical solutions to this NP-complete problems. Like the splicing model, biological operations in the k-armed model include cleaving and connecting.

2.3. Operations of the Adleman-Lipton Model

The basic principle of DNA computing is to use the encoded information in the sequence of nucleotides and evolve them by breaking and making new bonds between them to reach the answer. The basic operations performed by enzymes are denaturing, replicating, merging, detecting, and so forth.

According to the DNA computing models proposed by Adleman [2] and Lipton [3], there are several basic DNA operations. One important operation is hybridization which is a main process in DNA computing to form all possibilities of solution strands in which the right answer lies. Hybridization is done by mixing strands in tubes with the help of some enzymes.

Apart form hybridization, the basic DNA operations available on DNA are mainly the following.
  • (i)

    Merge. m(N1, N2)≜N1 ∪ N2 = N.

  • (ii)

    Amplify. Duplicate (N1) = N.

  • (iii)

    Detect (N).

  • (iv)

    Separate or extract. N ← +(N, w),   N ← −(N, w). Given a word w consisting of strings from Σ = {A, G, C, T} and a tube N, generate two tubes +(N, w) and −(N, w) which contain and does not contains the string w.

  • (v)

    Length separate. N ← (N, ≤n). Given a tube N and an integer n, generate a tube containing stands with length less or equal to n.

  • (vi)

    Position separate. N ← B(N1, w), N ← E(N1, w). Given a tube and word generate a tube with stands beginning (ending) with the word.

3. Grid-Based Clustering

The grid-based clustering uses a multiresolution grid structure, called cells, which contains the data objects and acts as operands of clustering performance. Traditional approaches include STRING WaveCluster, and CLIQUE [8]. The most common grids are regular hypercubic grid. This requires that the grid construction covers all the data space with the same precision. The second method uses flexible grids, that is, multiresolution grids with hypercubic or hyperrectangular cells having randomly oriented borders [14].

3.1. A Flexible Grid Definition

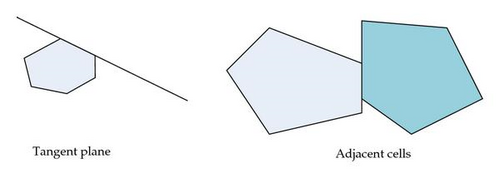
Suppose that the data set is Ω = {x1, …, xN} ⊂ Rn. It is bounded by a rectangle D0 in Rn. A grid is a undirected graph 𝒢 = (V, E) where each node of V is called a cell and is represented by a quad v = (D, c, p, σ), where D is a polyhedra, c is a center point of D, p = |ω∩D| is the number of points of Ω covered by the cell, and σ is the diameter of D. We will always assume that a cell is nontrivial; that is, D has interior points in Rn. For a cell v = (D, c, p, σ), its boundary is denoted by ∂D which is the set of hyperplane pieces bounding the polyhedra. If S ∈ ∂D and S is part of a hyperplane H, then H is called a tangent plane of the cell. Two nodes vi = (Di, ci, pi, σi), i = 1,2, are called adjacent if the two cells share a common tangent plane and D1∩D2 ≠ ∅. For two adjacent cells, define an edge between them. Hence, E = {uv : u  and  v  are  adjacent}. Figure 3 presents an illustration of tangent plane and adjacent cells.

Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Illustration of tangent plane and adjacent cells.

To construct the graph 𝒢, we need two parameters p0 and σ0 indicating the minimum number of points to be considered, and the minimum diameter. Then the graph is constructed iteratively. We start with the first node v1 = (D0, c1, N, σ1), where D0 is the original rectangle, c0 is the center of D0. Then at each step, the cell containing dense points (controlled by a threshold value p0), or with larger diameter (controlled by threshold value σ0), is split into two subcells by a hyperplane. A cell is sparse if it contains less points than p0. It is called a small cell if its diameter is less than σ0. If we reach a sparse or small cell, then add this cell to the node set of the graph. This step continues until no more cell left to be split. The resulting graph is called a flexible grid. Algorithm 1 gives the algorithm for the graph construction process.

    Algorithm 1: A flexible grid construction algorithm.

  • Inputs:   Ω = {x1, x2, …, xN} dataset of N points in Rn, D: hyper-rectangle containing Ω, p0:

  •    population threshold value, σ0: cell diameter threshold value

  • Outputs: V = {v1, v2, …}: set of vertices

  • Begin

  • V(1) = {v1 = (D0, c1, N, σ1)}. Let t = 1 and D1 = D0.

  • while V(t) ≠ ∅   do

  •   for each v = (D, c, p, σ) ∈ V(t)  do

  •    Choose a cutting hyperplane L passing c. Cut the current cell v into two subcells v′, v′′.

  •    For each v ∈ {v′, v′′} of the new cells, if pv < p0 or diam  (Dv) < σ0, add this new cell v

  •    to the node set V. Else add v to V(t + 1).

  •   endfor

  •   t = t + 1;

  • end

  • End

We present an example to show the data set and the flexible grid generated by the above algorithm (Figure 4).

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
An example of flexible grid with induced graph.
Next we define the weights on edges. A weight on an edge is the dissimilarity of the adjacent nodes. Suppose that the Euclidean distance in Rn is denoted by d(·, ·). Here and after, we will always assume that a data point x ∈ D means x ∈ D∩Ω. Then for two nodes vi = (Di, ci, pi, σi), i = 1,2, the weight is defined by
(3.1)

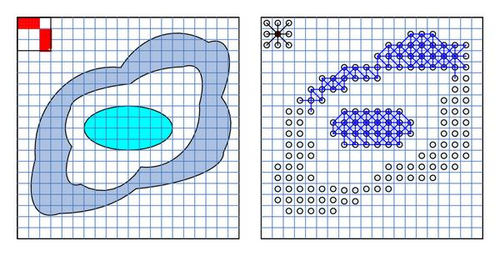
3.2. Clustering Problems

When the graph is constructed, the clustering problem is converted into grouping nodes of the graph into clusters. Traditional techniques include the hierarchical clustering [8] For the purpose of this paper, we will give a different approach for this problem. First it should be noted that nodes corresponding to sparse areas are outliers. Therefore, in order to reduce computing complexity, we first remove all sparse graph nodes with corresponding edges. We still use 𝒢 = (V, E) to denote the resulting graph, where V is the set of vertices, and E the set of weighted edges. An example is shown in Figure 4 with part of its edges.

Now we consider the problem of weight computation. By the graph construction procedure, we know that any node will correspond to a cell with diameter no larger than σ0. Therefore, the distance between cells can be approximated by d(c1, c2), and (3.1) will be
(3.2)
In this way we can significantly reduce the computing time without loss of much precision. Again we define a parameter 0 < ω0 ≤ ∞. We will eliminate those edges with weight ω > ω0. If this parameter ω0 = ∞, this means that no edges are eliminated. Now we use 𝒞 = {Vq : q = 1,2, …, k} to denote a clustering of the vertices set V of graph 𝒢 for threshold values p0 and σ0. Next we will use |Vq| to denote the number of its vertices. Define the energy of clustering as follows:
(3.3)

Then the clustering problem is a minimization of the energy functions. However, the optimization problem is hard to solve. We will present a variation in the following.

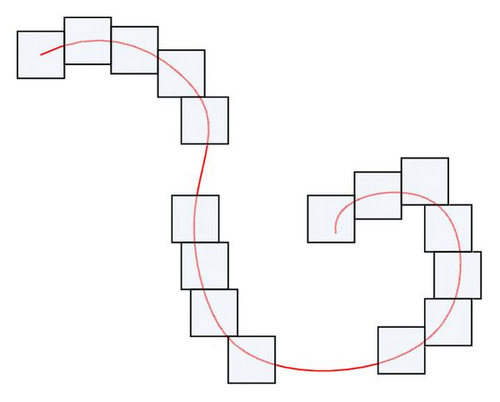
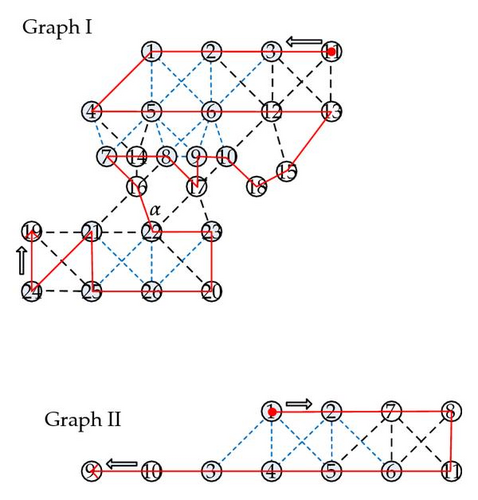
3.3. Path Clustering

Now we consider the graph 𝒢 = (V, E) with weight matrix W. Assume that the number k of clusters is a positive integer. A Hamiltonian path ℒ of 𝒢 is a path that visited each vertex exactly once. Now we remove k − 1 nonadjacent edges from ℒ and denote the result by ℒk. Define the energy E(ℒk) of Lk as the sum of its edge weights. The path with least energy E(ℒk) is called a path clustering
(3.4)

The first minimization of (3.4) is clustering for a fixed k, and the latter is clustering without fixing k. Path clustering is slightly different with distance-based clustering. The next example illustrates path clustering (Figure 5).

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
An example of path clustering with three clusters.

4. Clustering by DNA Computing

In this section we consider clustering of the graph 𝒢 = (V, E). We still use N to denote the number of nodes in V, and this will not cause any confusion. Suppose that the number of clusters is k which is a priori determined, or defined in the process of clustering. The problem is to partition the vertex set V into k clusters. Suppose that the original data set Ω is bounded by a constant M/2 > 0, that is, ∥x∥ ≤ M/2 for x ∈ Ω. Here we use the Euclidean distance for points in Rn and , where x = [a1, …, an]. Points in Ω are denoted by xi and Ω = {x1, …, xN}. A point in the data set Ω will be denoted by the lower case letter x.

For each point x ∈ Ω and a cluster C, define the distance between them as d(x, C) = min z∈Cd(c, z) where d(·, ·) is the Euclidean distance. If C1, C2 are two clusters, then define . Clearly these distances are bounded by the constant M. For u, v ∈ V define the dissimilarity measure as ρ(u, v) = ω(x, y)/M. Clearly these dissimilarity measures are in the interval [0,1].

Now we convert the dissimilarity measures into integers. First we need to define an acceptable error rate ε > 0. This means that we do not distinguish those measures where their difference is less than ε. Now we divide the interval [0,1] into I subintervals with equal width I−1 < ε. For z ∈ [0,1] let its corresponding integer be s(z) = [Iz] where operator [·] is the largest integer without exceeding it. Hence the dissimilarity measure lies in the set {1, …, I}.

Now we define the weight matrix on the graph 𝒢 by
(4.1)
A clustering of the graph 𝒢, denoted by 𝒞, is a partition . Thus any clustering can be taken as a rearrangement of the vertices v1, …, vN. For example, the vertex set {{v3, v2, v1}, {v5, v4}, {v6, v7, v8, v9}} with three clusters can be written as
(4.2)
Here we use the greed letter α as a separator between clusters. Therefore, we have k − 1 separators if we obtain k clusters. If we take dissimilarity measure into account, then a clustering will be as follows:
(4.3)

Now we have converted the clustering problem to a permutation problem. That is, any permutation of the set {1,2, …, N, α, …, α} (the number of α’s is k − 1) is a candidate solution. The string with minimum length is the optimal solution.

4.1. DNA Coding for Data

First we give the encoding of the dissimilarity measure, or the weights. In order to do this, we assume that 1 is coded by the string AG. And any integer i ∈ {1, …, I} is coded by seq (i):
(4.4)
Next we present the encoding of a vertex v ∈ V. This is done by using a fixed mer sequence as the following example (20-mer):
(4.5)

The separator α is also coded with a single-strand seq (α) of the same length with that of points. This is done exactly as the data point coding except that we need to distinguish separators with data points.

4.2. Encoding Scheme

Now we need to put everything together for a candidate solution (4.3). First we design a code for an edge uv ∈ E with weight w. This is done by linking the last half part of seq (u), seq (w), and the first half of seq (v) as shown in Figure 6(a). We need two special edges called the left half-edge and the right half-edge. The left half edge is a linking of seq (u), seq (w), and the first half of seq (v). The right half edge is a linking of the first half of seq (u), seq (w), and seq (v).

Details are in the caption following the image
Figure 6 (a) Designated DNA coding for an edge uv
Open in figure viewerPowerPoint
DNA-encoding architecture.
Details are in the caption following the image
Figure 6 (b) Designated DNA coding for an left half-edge
Open in figure viewerPowerPoint
DNA-encoding architecture.
Details are in the caption following the image
Figure 6 (c) Designated DNA coding for a centroid
Open in figure viewerPowerPoint
DNA-encoding architecture.

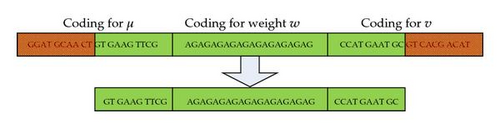
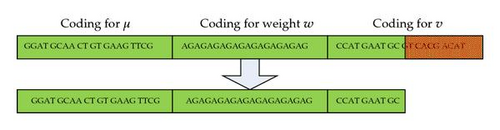
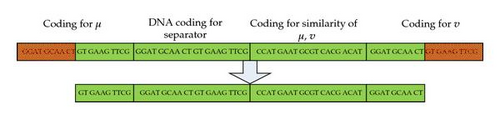
Next we define coding for a centroid which is a complementary form of a separator α. First for two vertices u, v ∈ V, we define its similarity as . One should notice the difference with dissimilarity measure defined in the matrix W. Now we define the code of a centroid as a linking of the last half part of seq (u), seq (α), , and the first half of seq (v) as shown in Figure 6(c). Here u, v are two vertices in V.

Finally, the code for a cluster 𝒞 is a permutation of the following string without changing the position of the left half-edge and the right half-edge:
(4.6)

4.3. DNA Program

Now we describe the biological operations for the clustering. First we put single strands in a tube T0 including complementary strands of all vertices, complementary strands of the separator α, and complementary strands of integers 1,2, …, I. These strands serve as splints. We also pour strands into T0 of all the left half-edges, right half-edges, strands of integers 1,2, …, I, all edges, and all centroids. Then hybridization and ligation can be executed. As a result, all combinations representing clustering schemes are obtained in the tube T0.

In order to select acceptable solutions among these combinations, we need to eliminate those strands which do not contain a separator α and those which do not contain all the vertices v1, …, vN. Finally, by counting the number of separators α as k of the strand with shortest length, we get the solution of the clustering problem. This final procedure can be implemented by direct observation to calculate the separator sequences by using special microscope such as atomic force microscope (AFM) to identify and calculate marking sequences [7].

The DNA program of biological operations is shown in Algorithm 2.

    Algorithm 2: The DNA program.

  • Step and Procedure

  • (1) Input (T0).

  •   All DNA sequences and complementary DNA sequences are placed in empty test tube T0.

  • (2) Amplify (T0).

  •   Make all sequences in T0 mixed together and execute ligation process. After hybridization

  •   process, all possible combinations of DNA sequences happen in T0.

  • (3) T1 ← +(T0, seq (α)).

  •  Select only those DNA strands which include at least one separator α from T0 and keep them

  •  into empty test tube T1.

  • (4) for i = 1  to  N  do  {begin  T1 ← +(T1, seq (vi))  end; }endfor; T2 ← T1.

  •   Select all DNA strands that contain all the N vertices v1, …, vN in test tube T1. Put them in

  •  empty test tube T2.

  • (5) Gel Electrophoresis.

  •  Find the shortest DNA sequence in test tube T2. Put them in an empty tube T3. This is the

  •  solution of clustering the problem.

  • (6) Count the number of separators α.

  •   Amplify and count the number of clusters in tube T3.

  • END

5. Examples and Discussions

In this section, we present some examples to illustrate the performance of our algorithm. Then we will show that our technique will give clusters more naturally.

5.1. Example One

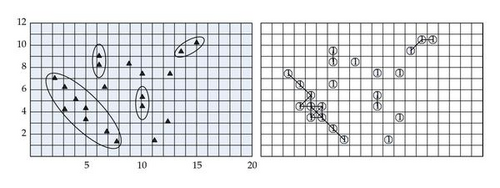
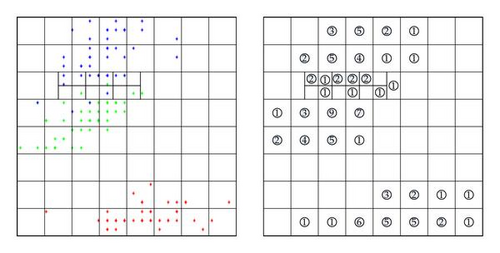
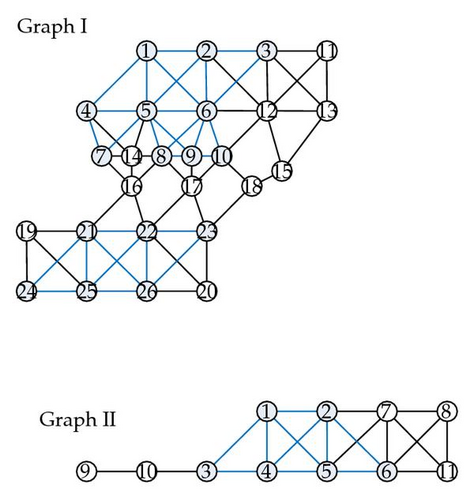
First we present an example with 20 points to be clustered that is discussed in [7]. First we construct a grid with interval 1 as shown in Figure 7. Then we take p0 = 1 as minimum points located in each grid. As a result, the induced graph is disconnected with 10 subgraphs. The final result shows four clusters with additional 6 outliers. This is different with result of [7] where they obtain four clusters with no outliers.

Details are in the caption following the image
Figure 7
Open in figure viewerPowerPoint
Data example one with graph generated with grid interval 1. Parameters p0 = 1.

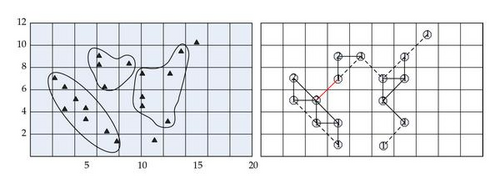
Now we change the grid into interval 2. Then we have only half the grids compared to grid with interval 1. We take p0 = 1 but we use another parameter ω0 = 1. This time we surprisingly obtain three clusters (Figure 8) with two outliers. This fact shows that the clustering method proposed here is sensitive to the construction of grids and parameters. Considering various definitions and measurements of clustering, this is not too surprising.

Details are in the caption following the image
Figure 8
Open in figure viewerPowerPoint
Data example one with graph generated with grid interval 2. Parameters p0 = 1 and ω0 = 1.

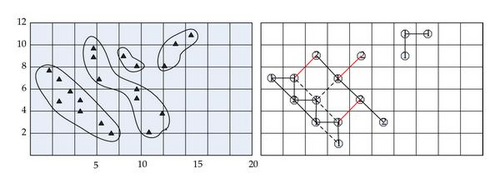
Now we construct a grid similar with Figure 8 but starting the first horizontal vertical lines not from coordinates (0,2) and (2,0). Identically, we can implement this case by moving the whole data set in the grid of Figure 8. With the same parameters as above, we obtain the third clustering result as shown in Figure 9. Now four clusters are generated without outliers. It is interesting to note that the three different grids induce one common cluster (left-bottom cluster). In fact, this common cluster is better organized than the other clusters. Hence we know that clustering is sensitive to the construction of grids especially for those bad clusters.

Details are in the caption following the image
Figure 9
Open in figure viewerPowerPoint
Data with different grid (interval 2). Parameters p0 = 1 and ω0 = 1.

5.2. Example Two

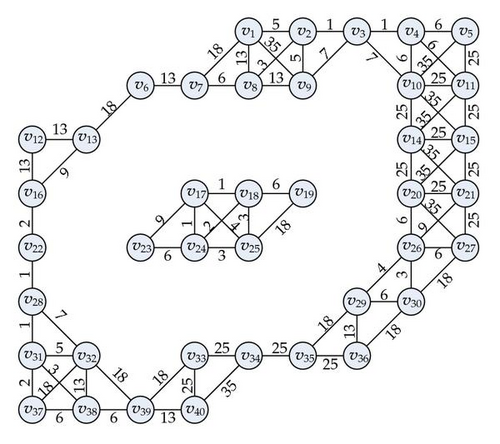
Now we consider another example as shown in Figure 10 with the data to be clustered and the graph constructed. For this example, we take p0 = 2. For adjacent cells, if they share a common edge, then we define their dissimilarity measure as 1. Otherwise if they share a common vertex, then define dissimilarity measure as 1.4. There are 40 nontrivial cells.

Details are in the caption following the image
Figure 10
Open in figure viewerPowerPoint
A data example with graph generated. The numbers in circles are the values of p in cells.
Since for any two cells p1p2 ≤ 100, we take I = 100 and by (4.1) the weight matrix is
(5.1)

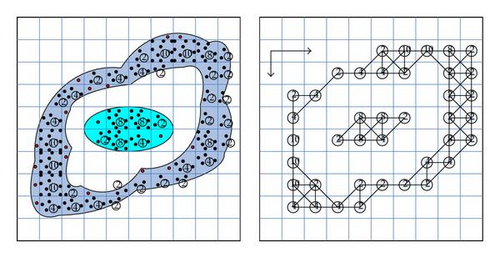
Here W1, W2, W3, and W4 are 20 × 20 matrices, and W is symmetric. The matrix W1, W3, W4 is shown in Table 1. The weighted graph is shown in Figure 11.

Table 1. Sample data weight matrix [W1, W3, W4].
0 5 0 0 0 0 18 13 35 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 3 5 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 7 7 0 0 0 0 0 0 0 0 0 0
0 6 0 0 0 0 6 6 0 0 0 0 0 0 0 0 0
0 0 0 0 0 35 25 0 0 0 0 0 0 0 0 0
0 13 0 0 0 0 0 0 0 0 0 0 0 0 0
0 6 0 0 0 0 0 0 0 0 0 0 0 0
0 13 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 25 0 0 25 35 0 0 0 0 0
0 0 0 35 25 0 0 0 0 0
0 13 0 0 13 0 0 0 0
0 0 0 9 0 0 0 0
0 25 0 0 0 0 25
0 0 0 0 0 35
0 0 0 0 0
0 1 0 0
0 6 0
0 0
0
0 0 0 0 0 0 0 0 0 0 0 0 0 35 25 0 0 0 0 25
0 0 0 0 0 0 0 0 0 0 0 0 0 0 2 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 9 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 1 2 0 0
0 0 0 0 0 0 0 0 0 0 0 0 4 3 18 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 6
0 0 0 0 0 0 0 0 0 0 0 0 0 35
0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0
0 0 0 0
0 0 0
0 0
0
0 0 0 0 0 9 25 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0
0 6 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 3 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 6 0 4 3 0 0 0 0 0 0 0 0 0 0
0 0 0 18 0 0 0 0 0 0 0 0 0 0
0 0 0 1 7 0 0 0 0 0 0 0 0
0 6 0 0 0 0 18 13 0 0 0 0
0 0 0 0 0 0 18 0 0 0 0
0 5 0 0 0 0 2 3 0 0
0 0 0 0 0 18 13 18 0
0 25 0 0 0 0 18 25
0 25 0 0 0 0 35
0 25 0 0 0 0
0 0 0 0 0
0 6 0 0
0 6 0
0 13
0
Details are in the caption following the image
Figure 11
Open in figure viewerPowerPoint
The constructed graph with weights on edges.
By the technique of this paper, the solution of clustering is a string. One of the clustering string as a clustering is as follows:
(5.2)

6. Clustering of the Iris Data

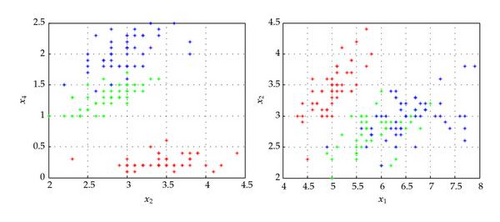
In this section, we present another detailed examples to illustrate the encoding of the DNA-based clustering technique proposed in previous sections. The new example is the well-known Iris flower data set problem. The Iris flower data set is introduced by Sir Ronald Aylmer Fisher as an example of discriminant analysis [15]. The data set consists of 50 samples from each of three species of Iris flowers, that is, Iris setosa, Iris virginica, and Iris versicolor. Four features were measured from each sample, and they are the length and the width of sepal and petal [15, 16].

6.1. Grids and Graph of the Problem

Now we use a matrix X|150  ×  4 to denote the data set. Then X is located in a rectangle [4.3,7.7] × [2.0,4.4] × [1.1,6.9] × [0.1,2.5] which is in the four-dimensional space R4. A grid cell (rectangle) D in R4 has 24 + 4 × 23 + 4 × 22 + 4 × 2 adjacent cells. If we choose D0 = [4.01,8.01] × [1.81,5.01] × [1.01,7.01] × [0.01,3.01] for instance, then the grids are defined as follows:
(6.1)

Then the cells can be denoted by 𝒟 = {Dpqrs∣20  ×  16  ×  30  ×  15} with 144000 cells which is a huge number. Due to this reason, we choose x2x4 among the four dimensions as shown in the first image in Figure 12 as cluster feature variables. The second figure in the same image shows the other two dimensions x1x2 which is studied in Qu et al. [16].

Details are in the caption following the image
Figure 12
Open in figure viewerPowerPoint
The Iris data figures for dimensions x2 − x4 and x1 − x2.
Next we design a flexible grid structure as shown in Figure 13. Choose parameter p0 = 0. Then the induced graph is shown in Figure 14. By (3.2) and direct computation, we obtain dissimilarities as matrices of the graph. Now we define the error rate ε = 0.001 and I = 1000. We cut the weight value by a maximum value 999. Then the weight matrices of 𝒢 are shown as in Tables 2 and 3. Here we write the matrix as
(6.2)
Table 2. Dissimilarity weight matrices W11, W12, W22 of subgraphs I.
0 67 236 67 118
0 100 56 50 283
0 177 500 500 707
0 100 198
0 50 106 79 106
0 133 99 99 250
0
0 125
0 125
0 395
0 999 999
0 999
0
0
0
0
530 0
158 0
0
250 354 0
250 354 354 0
250 0
354 354 0
0
999 0
999 0
0 500
0 354
0 354 88
0 118 113
0 152
0 333 500 354
0 157 143 200
0 37 236 83 94
0 16 39 22
0 40
0 125
0 50
0
Table 3. Dissimilarity weight matrix of subgraphs II.
0 167 79 67 94
0 141 100 354 500
0 33 167
0 40
0 100 183
0 500 707 500
0 999 999
0 999
0 999
0
0
Details are in the caption following the image
Figure 13
Open in figure viewerPowerPoint
The Iris data figure for dimension x2 − x4 and with grids and candidate graph nodes.
Details are in the caption following the image
Figure 14 (a) The number in node is its ID, and the number on edges is the weight value
Open in figure viewerPowerPoint
The induced graph with weight.
Details are in the caption following the image
Figure 14 (b) The number in the circled nodes is the population of each cell
Open in figure viewerPowerPoint
The induced graph with weight.
For the two subgraphs as in Figure 14, we can find Hamiltonian paths easily. For subgraph two, the path is
(6.3)
There exists many paths for subgraph one. One shortest path with indicator α along the edge v16v22 as shown in Figure 15(a) is
(6.4)
Details are in the caption following the image
Figure 15 (a) The shortest Hamiltonian path obtained
Open in figure viewerPowerPoint
A short Hamiltonian path for the induced graph.
Details are in the caption following the image
Figure 15 (b) The three clusters DNA method
Open in figure viewerPowerPoint
A short Hamiltonian path for the induced graph.

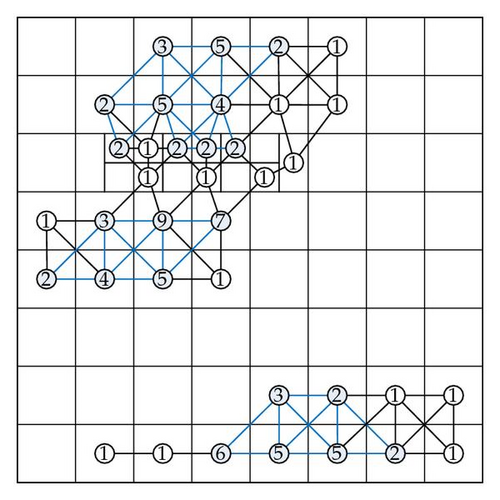
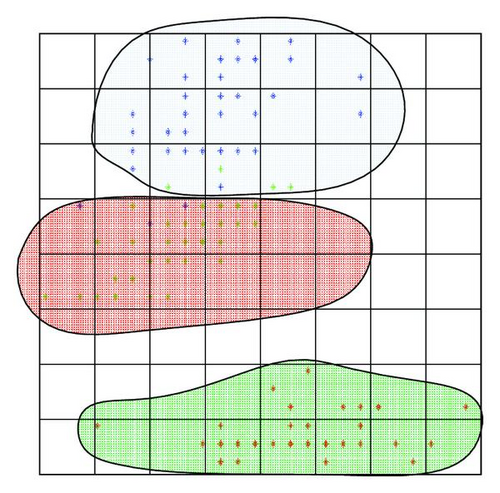
The detailed encoding scheme is shown in the Appendix. The final clustering result is shown in Figure 15(b). The number of points which is not correctly clustered is 7. Clearly this is much better than other methods such as CEPSO of [16] where the error number is more than 20.

6.2. Discussions

Now we present some discussions about the time and computational costs of the proposed technique in this section. According to Algorithms 1 and 2, the computational costs consist of two main procedures, that is, the grid construction and biological operations, and we will show that the complexity is roughly linear.

First we check Algorithm 1 for the construction of flexible grids. The time complexity is the total searching counts where |V(t)| is the cardinality of V(t) and T is the final t that V(t) reaches null. Clearly |V(t)| ≤ 2t. Now we estimate the upper bound of T. In the worst case when V(t) consists of 2t cells, and each cell has a data population larger than p0, we have
(6.5)
There we obtain the estimate T ≤ log (N/p0). And the total time upper bound is a linear time as follows:
(6.6)

Next we analyze the complexity of DNA program as proposed in Algorithm 2. It is clear that the DNA program consists of three searching procedures. Step 3 selects those strands which contain at least one marker α which is a O(1) operation. Step 4 checks if we get a sequence containing all the vertices with a complexity of O(Nv), where Nv is the number of vertices and Nv ≤ N. The final Step 6 counts the number of α′s and splits the sequence into clusters. For the shortest sequence which contains all the vertices, the maximum number of markers α is Nv. Hence the total DNA complexity of the program is O(N) which is linear.

Finally we make some comments about experiments. By Adleman [2] and Păun et al. [1], when we design a DNA program for solving the problem, a test tube (as taken in the laboratory) is considered a multiset of words (finite strings) over the alphabet {A, C, G, T} with basic operations proposed as in [1, 2]. These basic operations are standard and biologically implementable.

However, when we want to simulate the algorithm with personal computers, there will appear some tricky complexity that lay behind the biological operations. Again we analyze the steps in Algorithm 2. First we consider Step 2, and we only consider generating sequences containing each vertex exactly once. The time complexity here will be . By examining other steps, we find the total time is O(2N).

7. Conclusion

In this paper we presented a new DNA-based technique for spatial cluster analysis. Two examples are given to show the effect of our algorithm. We do not need the number of clusters in advance. By a flexible grid method we can reduce the size of searching space significantly. This is different with other DNA-based applications in that they enumerate all solutions which will produce a large search space. This is especially useful for large database even through DNA computing that has large parallel ability. Also by changing the grid and corresponding parameters, we can get various clusters.

Finally we will point out that nonconvex clusters can be easily obtained by the technique of this paper. Comparing to research in [7] where only convex clusters can be generated, this is useful for complex database to be clustered. Up to the authors knowledge, this is, the first research in cluster analysis by DNA computing for nonconvex clusters. It provides an alternative solution for this traditional knowledge-engineering problem, which is not a combinatorial in nature. Comparing the many applications of DNA computing mainly in combinatorial problems, this is still interesting.

Acknowledgments

Research is supported by the Natural Science Foundation of China (no. 61170038, 60873058), the Natural Science Foundation of Shandong Province (no. ZR2011FM001), the Shandong Soft Science Major Project (no. 2010RKMA2005). The authors are indebted to the referee for important suggestions and the supplement of Section 6 and Appendix of the Iris Data Set Problem. We are also indebted to Dr. Qi Feng and Dr. Xue Jie for help in the design of DNA coding.

    Appendix

    DNA Encoding of the Iris Data

    In this appendix, we present a DNA-coding scheme for the Iris data problem. By Tables 2 and 3 the weight values range from 16 to 999. Therefore, we need a maximum length of 999 mer to code the weights.

    First we present one coding scheme for vertices of Subgraph I.

    VERTEX CODING: 1. GGCCCATT GTCGACGA 2. AAGCATCC GAACGTCT 3. ATTTAGTA ACTGTCAT 4. CCACTAGG CATTTACT 5. TAACTGAA TAGCCTAA 6. CCCATCCT GACTGCAT 7. GATGTGCT CGTAGCCT 8. AACCCTTA CGTGCATC 9. ATGCCCAA CATATAGG 10. TATTTAGT TGAAGCAT 11. TTCAGGAG GTGCACTA 12. CGTTTAGC CACCTTAG 13. TGTATACA CTTTATGT 14. CAACCATA GCCGCCGT 15. TCCCCGTC ATACCTTG 16. TAGGTATG ACTCGGCG 17. AGAAATCG GCCGCAAT 18. GAGCGACT TCCTGGGT 19. CAATCATT TGCGGAGT 20. GCCGTGAT ACCCTCAG 21. AATGCACA GAGTTTAA 22. TAGACTGT GTAAATCG 23. TCTACCGC CGTCCTTG 24. AATGAACA TTAGTGGC 25. TCTGCATA CGCCCCGT 26. AGCGTTGT GTCCTTCT

    Since the edge coding of vjvi is similar to those of vivj, we next only present coding for one edge between each two vertices as follows.

    EDGE CODING:   1-2: CAGCTCGT  GGCCCAACGCCCATTTCGTACCACGAGAACCCAAATAACGGAGCATAGAAGGGCATCTTACTTGGAG  TTGCTAGC 1-4: CAGCTCGT AGCTACACGAGCTTCCGTATCGCTGTGTCGAATGGTGGGCCTTCTGTGGGAGTTAGGGGG  CCGCTCAGACCCAGAATCGACCTGTTTATGCTGCCAGCTGTCAATGAATCTTAGAGTGTG  AACGACATATCCTGTCGATTGTAG   ATTGTTATCCTTGAAGAGATATACTTCGGCTTAGGC   CTAGTTCGAAGGATCAAAACTACGCGTCAAAATCGGTCGCCGTTTATACCCCGTCC GGTGATCC 1-5: TTGCTAGC AACGCGCGGCCACCCTTAACTACCCAGTACCCACATCTCCTCTGGCATGTTGGG  AAACTCGGGCTAT  ATTGACTT 1-6: TTGCTAGT  TACAAGAAAGCATTAGACCACAAATATCACGCGATTAAATCAATGGCTTAA   AATCGCTGATTCATCGGTTAACAGACAGCGCTAGGTTACCGTGATACCGTAGCACTCGATCTTAGTC   TCCTAGGA

    2-3: GTTGCAGA AAACTTGAAGAAGCGTCAACGAGTCGGACCTTGGCACTGCTGGCGAGATCGCCGGACAAAATATGCATGTGCCCCCTACTTAAGGTAATCCGATTAGAGC TAAATCAT 2-5: GTTGCAGA CCACAGGAGATATGATATATCCTCGGCCACTGAGCCCTAGGCAACCCTGGTCTAAT ATTGACTT 2-6: GTTGCAGA GTAACCGCGAGCCCTAACGCTTACTCTTTGACGGGAGTCACGAACTGACG TCCTAGGA 2-12: GTTGCAGA GGCACTTTGA GATGTCGGTG AAACTGTCCT CCGATCTCAA CACTAGTGTG GAGTCTTCAC ATCACAATGG AACTCATACG GATAAGTCAG TCTGCCATGC CACAGGTAAA ATATGAGGCG AGGGCAG CTC TGGGCCTTTG TATCAGCCAG GTTCTATTGT TTCAGGGCCC TGGTTAGGCT GCAATCAAAT ACCCATAGTA TTTCTGAGCA CAATTCCAAA TGACGCCCAA ACAGACGTGG ATAAATTGGT ATGAAGTCTA TGACCGTTAA ACGGAGTTAC TTC GCAAATCG

    3-6:  TGACAGTA  GTTTGGACAA  TGCGAACTGC  GAGGTATTCA  GTTAGCAGGG  TACCGACAGA  ATATGTCCAG  AAGCTT  TGTT  GGTCTAAAAA  GTCACGGCCA  ATTTGCTAGC  GCGGGCTGTT  ATACGCTCAA  GATGGGCACC  AGATGATATC  CTCATCATTC  GGCCGCAAGT  GACTCTTCGA  TTATACT  TCCTAGGA  3-11:  TGACAGTA  GTCCAGGAAC  CCCTTATTTT  TTTGAAAGTT  AACGACCGTT  CTACCCGACG  TTAGGGCTGA  CGCCTTCCGT  ATACCAACAG  CAAGATTACG  TGATGACGGA  CCAAATATA  G  CTCGTTGCCA  CAAGGGTACA  ACTAGGCTTC  GACAATGTAG  AGGAACGCAA  CGGGTCTGTG  TCCTTCACAA  ACCTACCTTT  GGGAGGGTAG  TGCTTGTTTT  TATATCTTTC  TATGAGCCAG  AGAGTCGATG  GCCTGATAAG  GCTGCCATCG  GCTAATTGGG  TACTTCGGCG  CTCCCGAATA  GCCCAATTGT  GTCAGCGAGA  TACGGCCCTT  GTGTTCAGCA  TTGCCCTGTG  ACAATTCATT  GTACGACCGA  CGCCCATCTA  TGGGTGCGGG  GGTGGTTTAA  AGAATTCTAG  GTGCTACCTG  CGACTCACCA  CCGCTGTTAT  GACGGGGATA  GTCGATACTA  AAACTACCAT  CATATTCATG  CTCCGGAAGA  GCCGGCCAGT  ATAGGTATTC  AAGTCCTC  3-12:  TGACAGTA  CTCAACTACG  TTTAATTTAT  GCGAAGCGAG  TGATTAACCG  AAGCGAAGGG  TAGTACGGCT  TCTACCGCCA  GAACACGTAG  ACAGCGTGG  G  AAAGCGATAG  TTGACAGCTA  AGTCGGTTGA  GGCTGCACCC  TGATGAACT  C  GTAATACATA  GCTCAAGCTT  CCATTGGTGG  ATTCTTTACC  GTAGTACGAC  TCACCCACAG  GAGTCGACAC  TGTTGGCTTC  ACTTCATCTA  TCCCAGGGCT  TTCCCGTTAG  CAAGGCATTA  TTAGACAGGG  TATTGCCGGA  CTAGCTAGCC  TTAGCTATAA  CAGGAAATAA  TGCTGATTGG  ACTGAACAGC  GATGTGATTC  CTCCAATAGC  ATATATCCAT  CGCCGAGTAT  TCTTCGGTTG  TTCGCGCATA  CTTCCTAGGA  ATACCGCCGA  TTATGAATTC  GCCCCAGGGA  GAGTCCGTTC  CGACCCATGA  ATGATTTCAC  CGGTCGCTGC  GCTCGGTTCG  TCATCTTGTG  GCGAAAGGTC  GCAAATCG  3-13:  TGACAGTA  AAGAAGCTGG  CCACATTCGT  CACCTAGCAT  TGATTGGCGA  TGTCGGTGAG  GGAAATTGCC  GCGGTACCAA  GGCAGAACTT  GCGGAGTCCG  GTGAAGTATG  GAACGCGGAA  CACGAGCCGT  AGCTAGTTTG  ATGCTTTAAA  AGCTTGAGAA  ACAATACAAC  CTGCCTGAAC  CACGCTGCAG  CAAGACGCGA  GGCGCATTTA  ATGGCGAGGT  AACCAAGTAT  GGTCCCCACC  AGCTAACGAG  ATTAGCCGAC  AGAGCATTTC  TTTGATGCAA  CGATTAACGC  GCTGGTCGCA  ATGGTCCCAA  GGGCGAGGGA  AGCCCGGTTA  TCAATGAAGG  CCATTATGGG  TAATCCCATA  GACCAGGCTT  GGTCAGAACC  CTATCCTAGT  AAGTCGGACG  TTGGACGTTG  CAAGAGTGCG  AAACATGTCC  GCATAGCGTT  TGTAAGAACT  ATCGAGGAAC  TACCTTTGTC  GATTGTCTAG  AACATGCCCA  TGAAGAGAGC  ACAGACATGC  CAACCCCAAA  TTATGTAGGA  AGGGTACGGT  TCTAAGGTAT  AGTTTTGAGG  TTGTTCTTTT  CGTCTACAGA  AAAGATCCCC  TCCGGGAGTA  TAGTGCAAAA  TCCATGGAAG  AGCCCACAAA  AGTCAGAAAT  AGACTAATAT  TCCATGTTAT  CAATCAAGTT  AATGCTTCAA  CAAACCCTGA  GCGTGCGCGA  AGAAAAGTAG  AGATTTA  ACATATGT

    4-5:  GTAAATGA  GAGAGGATTC  CTGAGCTGTT  CAGGCGGCGA  GGCATCTAGG  TGGTGCGGCA  AAGAGATCTT  CTTGTGTCCC  ATCCCGCCCC  TACCACTTAG  ACCAAGACGA  ATTGACTT  4-7:  GTAAATGA  TAGTGTGCTA  GACATCTGGC  CGCCGGCGCC  AGCTCGTGGA  TGCTCATAAG  GCTTAACTTG  ACGTCTTAGG  AAGAAACTCA  AGCCCAATCG  CATTCTTCTT  CACTGCAACA  CGCGGTTGTT  ACCGGCCTTT  GAGTATCTTT  TACTTCGCTT  TAGGCCCACC  TGCAGTAACC  ATCGCTGTCA  GAAT  TAGCTG  AACTTTTG  CTACACGA  4-14:  GTAAATGA  TGCGGGTGTC  TAAGAAATTT  GCATGAATAA  GTGCTGACTA  AGTTATACCG  AAAAAGTCTT  GCGGGACGCA  GGTTGCTGTC  TCGTATCTCT  GAGAGCTCGT  GTCCGTTCGG  CCGGGACGAT  AGGATGCCCC  CGACAATGAA  CATGATCTTC  GACCCACAAC  GTACAAGACC  CGAGCTAACA  CTGCTCTAGT  CATCCACGTA  TTATTATTAC  TACCACTAGC  CAACGTGCAT  CCCGCGTTGT  AGTACGCAGG  CTGTTTCACG  ATGGCGATTT  CCAACGGAAA  GTTCTAACTT  GACAGCGTAC  CACTAAAGGA  CGGCCAGGCA  TGGGCATCGC  AGTTTTGAGT  ATTCACTCCG  TGCACAACCG  GACCTGACGT  ACGTGAGGAC  GAGGTCACCG  GAACTAGACT  CTATCCTCCG  CGGGCACGAA  CTATTGACTT  CAAACGTACG  GACACCTATC  TTAATAGAGG  ATTTGACGCA  TACTCGCTAG  CTGCCGGTTG  CCTCGGCGGC  GTTGGTAT  

    5-6:  CCGGGTAA  CGCGAATCGC  GGGTAGTTCG  TATCGTTGGA  TGACTGCACT  GCACATTTGC  TCCTAGGA  5-7:  CCGGG  TAA  ATGTCAATTC  GGTAAGGACG  TGGTGACATT  GATGCATCTG  CTCAGTGTGC  CATATTCGTG  CTCACTTCTT  GCGCTATCTT  TCGAGGGGTG  TCACACACCT  CTCAAG  CTACACGA  5-8:  CCGGGTAA  GTCGCCCAGC  TATCTGCCGC  AGACAGGCAT  ATAA  CGGAAG  GTATGGTGCC  GTGCAGAGCT  TTTGCGCAAT  ACGCATGCA  TTGGGAAT  5-9:  CCGGGTAA  GGCTCAGGCA  CAACTGAAGA  TTGACACACG  TATAGCCAGC  CGACCAACTA  ATCACCACCG  CGTGGGCTGT  CTCGATTTTG  CCCACTATTT  GCCGGGTAGA  ACGCGT  TACGGGTT  5-14:  CCGGGTAA  TTTCTAGCGG  GCCGCCATCT  TACTGAGTAG  ACAAGGAGGG  CATTCTGAAC  TTTACTTCAC  TATCGAAGCG  AGCGCCGCGG  GCTGACAGCG  ACAGTACACA  TAAACGTAGT  ACGTATATTC  CACCACAATG  CCTTGCCACC  GTCACCGCGA  GTCTAGAC  GTTGGTAT  

    6-8:  GGGTAGGA  TGTACCCTCG  CGAGGGCGCC  AATTGCTAAG  TACAATAACC  CCACTGCTAG  GCTATACACG  ACGATCTAGC  GTTCCAGTCG  ACTCGCCCAG  CTCACGATAA  TGTGTACGCA  ACAACGCCGC  TGTCGAGCTC  CAT  TTGGGAAT  6-9:  GGGTAGGA    GCGCAAGACT  TGATGAGTGA  TCGTCCGTTC  TGCCCGTGGA  GATGCTGAAG  CTCATACAGT  ATGGCGCGCG  ACAATCACTA  TGCGGTGAAG  TGTGGCCCC  TACGGGTT  6-10:  GGGTAGGA  GTGGCCGGCT  CCGCCAATCA  GTCCACACGT  TGATGCCTCG  GGACGACTCT  CGCGTAGAAG  AGTATGTACT  GGGACCCAAA  AAGCTTGAGA  GGATTTCGA  ATAAATCA  6-12:  GGGTAGGA  AAGGAGAGCT  CGGGGGGGAT  GTTTATGAAG  AAATGCAGTC  AATACACTCT  AACATCCTAC  CCGAACAATC  ATGATTAAAC  GTAGTAGTTT  ATCCTATAAT  TCGCTCCGCC  CTTGCCCCAG  AAGCGATCAC  CACCCACTAC  AGTATACTGG  GCTAACATAC  GACGATTAAG  TACCTTGTGC  TAACCTCAAT  TTCGCTACGC  TCGTTGGGCT  TATACCTACT  AAAGCGAGGT  CTACCACCTA  CCCTAAAAAA  GCAAATCG  

    7-14:  GCATCGGA  AGTAAATCAC  GCCTTCATCT  GAAGGCGAGT  CGACCTACTT  TCAGGTCGCT  TTAGAATGCT  ATATGAGATG  ACGGAGGCAT  TGGTTAAGTA  CAACCTGACC  AGCAACAACG  AGTGGAACGG  AGAGCGCGTA  CAACTATATG  TCACCTCATC  TAAAAGAGCT  TACGAGTTAC  TAATGTACGG  TGGGGAAACG  GCTGAGTCGC  CCCTCCGGTT  GCTCCCGGGT  AGAAGCCGGA  GACGAGCACC  GTCCACAGGG  GTTGGTAT  7-16:  GCATCGGA  TGAGCCAGGG  ACTGAAACGG  TACCACCCAG  TCGTGTGTTC  TGGTATCTTG  GGGCCGCCCT  TATCGCAGCG  ATGTCTCCAA  GAAGGTCGTC  AAAAGCAGAT  GGAAG  TTGAT  GCATTCTCTG  GCCGTAATGT   ATGTAGGATA  ACCCCTTAGT  TCCAAACTGC  AATCACCCAT  TGATAGTTCC  ACATGTCCTG  GAATTAAAAA  GGACCCTTAC  ATCCTTAGCT  TATGAGGTGC  AGAATCCTTC  TCTGGCGGCT  ATGTAGTAAG  GTCACGAACG  TAGGTAGAGA  CAAATCCGAG  TTGATTCGCC  ACACGTTGGC  CGAGGCTCCG  AGAAGGGGAC  TTCAGACTGT  TCTGGTTACC  GCTG  ATCCATAC

    8-9:  GCACGTAG  GAATGAGCTT  AAACTAATCA  GTAAGGACCA  GTCGGGGAAA  CTCTAGCCCA  TTGACCACCA  GTTATTCTCG  TCGGGTCGAG  AGGCTCACAG  ATAATTTAGA  TACCGAGAAG  CGAGTCTTAG  GGGAA  TACGGGTT  8-14:  GTATAT  CC  CGGTACGATC  AGAGACCCTC  ACGCAGCAAC  ATATAACAAT  GCGGAAAATC  TCGTGTCTCA  AATGCGTACT  ATTCATATCT  GTTGAACACT  ACTAGGCCGA  ACGCAATGTT  GTCAGGCCAA  GCCACCGGCT  ATAGGGATTT  ATTTTACCCT  CTTAGGCAG  G  ATTAAATAGG  GGCCAACCAG  TTGCTGGGCC  TGGGTATATG  TAATGCCTAA  CCATAAACAG  GAGGGAACCT  GGGTTCAGCC  ACACCATGCA  GTCCACAGGG  8-16:  GTATATCC  GGAGAAGCGT  GGCACCCTTG  GGGGTAACTC  TACATTCACC  CAGGAGG  GCC  TCTCCGCTTT  CAACTGGGCA  ATCTAACATG  TGTCCACCGT  GTACCGGTAG  CGCTACTGCC  CGCTTCAAGA  TGTAAGCGAG  TACGCGTCAT  CTGTTAGCGA  TGAGCGATTC  TAGCGGGACG  AGAACAATAG  TAGAGTCAAA  CGGCTTGGAG  CTAGAC  AGCT  TGTTTCTAAA  CAACACTTAT  CATTGCAACG  GTGGGGGTAA  GATATTCTTT  AATGGACTCG  CTAATATATG  GGCCTGTTTA  TGAGGACGCG  GAACGTAAAT  CCACCAAGGT  CCGCCGAGTC  ACATTCTTGC  CTATCGTAAG  CACT  ATCCATAC  8-17:  GTATATCC  ACCTCGATGG  ATTTCTGGTC  TACCCAGGCA  ATCGTTGATT  CCCCAATGGC  AACTCCAGTA  GGGTGTTACC  AATTCGACAC  CTCGCAGATC  ACACTGGCAC  GGTGAGGCTC  TCCGGCCGAT  GATGGCAAAT  CGGGTAATTC  AGATGGGTAC  AATTTGTTGG  AGAAAATCGT  GGCGCTTTGC  TTCGACACCT  CGGGATCGGC  AAATCCAGTA  GCGTGTATGC  TTCGCATCCA  GCGATGTAAC  CATCCTTGAT  TAGACGCAAA  AGAAGATCAT  GGACCGGTGC  GGCGGGGATA  CAATCGGTGT  CTGGTGTCGA  CCGACTGGTC  CACCATCCCC  CGGTGAGGGT  ACGCGGTTGA  TGAA  TCTTTAGC

    9-10:  GTATATCC  TGGGAGCTGA  AACGAAGTCG  ACACACTCAG  CTCACCGCTA  AGCTAGAGGG  GGAAGTACCT  TTGTATGATT  CGGCTTGTCA  GACTATCGAC  CAGGGCTAGG  ATACTGACGG  TGCAGATCAG  GTAGC  ATAAATCA  9-17:  GTATATCC  GTACACAGCA  GCGAGTCACA  GACTCACCCC  CACCCCAAAA  GCATCGTGAT  CTGTTGCCGA  CTTGCGTTTA  GCGCGTAAAG  TTTTTACTTA  GTATCTTACT  CTCATGTAGC  GTTATAGATA  GACAATTCAT  AGATCAGTAC  TACAACGGCC  CAGTTCT  TGC  AGCGGATTGC  CTATTAAATT  CGGACTTGTG  AGATTTGATG  ACCAAGTTAT  AAAGGGTTCG  TATTTGCAAT  TCGCTGGTCT  ACACCAAGCG  TCTTTAGC

    10-12:  TCCTAGGA  AATGTCCGTT  CGGCAGGTTC  TACGTTTAAT  AGGTACGTCG  GGTGATTTCA  CTATCCGCGC  TCACCCTAGC  CATATCGATC  TCACATCGAT  CCGGTTAACT  CGTTGCCCGT  GCGGGAGGCT  GCCGTTTCGG  TAGGGTAGCA  CTTTG  AGGAA  GAAGCAGACC  GAACACTGAG  TGTCGAGACC  CATAGCTGAA  TTAAAGCGAG  CTTAGGGTAG  GTGACAGCTG  CGG  GCCAATT  TGGCAGCGTC  GGACTGAATG  ACATGGAACC  GGCCTGAATC  TGCGTGATTA  TGAAGCTATC  GCTTCTGGTT  TCTCAAAACA  AACTCTCAGA  TGTGTTGCAC  CCACAGGTCG  TCCTTGGTCC  CGAATCCAGC  CTCATTCTTG  GGATCGACTT  AGAGGTCCAA  AGCTT  GCAAATCG  10-17:  TCCTAGGA  CCCAACTTAC  ATAGGGATCA  GAGTAACTTC  ACCTGCTACT  CTAGAGCTGT  CAGGTACGCC  CACTCACGTG  AAGCACACCA  GTTTACTCGT  CTGAACGTTC  GACGAGATAT  TCGCCGGTAT  AGATCGCGCC  CTTTGATTTC  TGTGCTCCCA  AAAAGGATTT  AGGTGTCAGA  ACTGGTACTC  CCGTAACGTT  GGCTTTTAAG  AGAGGTGCGG  CTGTTCGGGA  CCGTTCGTCG  TGTCGCTCCA  GGGTTCCTGG  GTCGACATTC  AGGGAGAAGC  AAACAAAA  CG  TGGAAAAATG  AAATCGCATG  ACTTGCATGT  TACTTATTTG  CGGGACGAGA  TTTTAAGGAA  ATTGGTACCT  CTAG  TCTTTAGC  10-18:  TCCTAGGA  GATTACACCA  CACGTACACA  TAGCTTCCCA  GATCCCTCAG  GTCAGCTAAA  TGACGCCCCC  ACAAGACGGC  TACGCTTACC  ACCAATCGTA  TCCGCGTGCA  GTCCAGATGC  GGCCCACACA  GGCATCCAGA  AACTAATTTG  ACGGTTCTAC  CACGACTGTC  GAAAATTGCG  ACGCCCAATT  AGAACAATAC  CGTAGACCGC  GCGTTCTTGT  CTAATTCTGT  TTCCTCCGGA  AATTCCATAC  CGTTGGATAC  TCCGCCGTTA  AAGGGGTATG  CTTCCGAACC  AACAAAGGTA  GATAAACGCG  ACACCACGGT  CTATTATACA  TCCCCTGGCA  ACCCCGGGCA  CATCGCTCGT  TTGA  CTCGCTGA

    11-12:  CACGTGAT  TAATATACAA  AGACAACACT  GGCATTCCAA  GTTCAGTTCG  GTCAACAATC  CTAGATGGGG  CGAG  TTCATG  ACGTGGAAGC  CCATCAACAG  CTGCACTTCG  GGCAAATATG  GTGCCCAAGG  CTAGTCGCAC  ATTACGACGA  GAG  AGGCACT  GCCCTAGACC  CAGGCACAGG  CGAAGGAAAG  CGCTCTGCCG  GCGACCATAT  ATAAATGACG  GCTTAAGGTG  GAATGACATA  AAGCCGTCCC  CCCAATCGGC  TTATATGCAA  GAGTACTGGC  ATCAATCCTT  TAGAGGCGTG  TGGGACTGGC  CGGTAAAATG  GCATTTAGCC  GAACTGACTA  CCGCACCAGA  AATGACTAGT  CTTCAGTAAT  CGTTTTCTTT  ATCACAGGAC  GTTCCTCTGG  GCAGATTTGT  CACGGTCCGC  GACGCGCACT  TCTGGTATAA  TACTATGATA  TTGGAAACAA  CATGCCAGCC  TCTACGCGCA  CTTGGGCAAA  CAAGGCTTAG  GTCCAGATGA  TTTCTCTCCA  CGAGCACACC  TGCCGTAAAT  GAGAGATGCG  TTTAGGAGTC  GCACCTATAG  GTCCTCTGCC  GCACGAGAGT  GTTTATTCCT  CGCTCTGATT  TCGAAATATT  TCACAAATGT  TCTAAGCTGC  TTATGCTTCG  TGATTTGACC  CCCGTTGGTT  AGCAGAATCT  GCAGTCAATG  AAGCTATTCC  TCCATTCACC  TGCAAAGTAA  ACAGCGGGGT  GATTCAGGGA  TGCAAGTCGA  TGGCCTAGTA  ATGTGAGGTT  TGATAAGTCA  ATACTTAT  CG  GAGTATCATT  ATTGCTTTTT  GACCCCTTGG  GCGGACAAGA  ATCTACAACG  ACGAACCGCA  AGATAACGTT  TAACTTACAT  TGTTCACGTG  CGCGGCCGGC  AAAATATACG  CGAGAAAGTC  AGCTGTGTTG  GGCAACCGGC  CAAGGACTTG  GACGCACCTC  ATCGCAGCTT  CGCACGTAAT  TGGAGCGACT  GTCAACTCAA  TAGGTGCCCG  TAACTCTGC  GCAAATCG  11-13:  CACGTGAT  TGTATCTCGC  ACACCGTTTA  ACGTCTACCT  TAGAACCCCC  TGCTTTGCAT  CATTTGTCTG  AATGGCGGGC  GCGATTGGGA  GTTCGTGTTA  TATAATTGCA  GTCTGGCAAT  AGAGATTTCG  CGCAAGAAGG  TACAGGCGCC  CGACGCCCGC  ACGCCCTCAC  ATACCTTCTC  TGTAATAGCA  ACTGTCGCTC  CGGAGCTCGG  GATTGTACCC  ACATGGTTGT  GGTCTCTATG  GCGGGGAAGA  GAACATGACC  TTTGACCTGT  GTCCCGTAGC  ATCTTGGCGT  TCCTACTTGA  GTGGATATTG  ACCGAATTAA  GACATACAGG  TAATCTCGGC  CGTTTGGAGC  GCAATCCGCC  GCTTACATTA  TCAAAAATGA  ATGCCCGGTA  CCACATATTC  GTCCCAGGGT  CTTCTAGACC  CCGTCCTGTG  TATAACCGAA  CCTCAGAACC  AAGACCGCCT  ACTACTGACA  ATCCTGCGCC  CAGAGCATCC  CTAAAAGTGG  TATTCTAAGG  ACGCCGCGCT  TTACGATTAG  CGCTCATCGT  TGTATTTAGT  TTAAAATACT  CTTAAGCGGT  TGATGCGTAG  GCCGCAATGG  TTTCGCAAAG  GCGTGGCACT  GAGCTGCTGA  ATAGTTGGGA  GAGGCAAA  GT  GGAATTTCTG  TTCCAAGCGC  CAGGAGACCG  CCAATGGAGC  TTTCATTCCC  AATAGGGACT  TGATAATAGT  CGGCGGCATA  GAACGCTGGA  TACAGCCATA  TCGCCTGGCC  TCCAGCCAGA  AATCGTGCGC  CAGTAGTTAG  GCAACTCACG  TTCGAAGAAT  TGGACCTCTA  GTGTGGCTGA  AAGCTCGGCG  CCACCAACAT  GCAATTACTC  TGCCCATATG  CAGTCCGCCA  TTGGCCCTCA  ATATACCCAA  GACAAGGGGA  CGGAGATGAA  CTCCACTGGT  CGGCCACGTT  CGAGGGGGGG  CATTGCCGTG  TGGCATCCGA  TGGGTTCGCT  TCTACCCTCG  AGTGTTTACC  CAACGCTGTA  CTGGGGTTC  ACATATGT

    12-13:  GTGGAATC  AGGACCGCAC  GGTCATTTGT  TATTGTAACA  CCTTGACAGG  CGGCAACGGC  TCGCCGGCAA  GATACGCGAA  GAGGAAATGG  CGATTGAGGA  TCTCAATTCA  CTGGCCCCGA  CTCCAGTTAC  TGCCTCGATT  TAGCTATGTT  GCGAACTACA  CGCGCTAGAG  CAGCGTAGAT  ACAGCTGACT  CCCCTAAGCT  GTTCCCGCGA  AGCGTTATAG  CGAATTTATA  GC  TCGGGCAT  GGTGGATGGA  CACCGCCCGG  CTGACGCGTG  CCAGGCCATG  CAAGTCAGGC  TTCTTGTTTG  AGAACTAAAT  AGCATCACAC  CAAAGCTAAA  CGGTCGGTGG  GGTGGTCGCA  TGTGCCTAGT  CCTTCATGAA  TGGATTCAGG  CTATTTCAAG  AGTTCCCGCG  CACGAGGTCG  CGATGTATAG  GGGTTAGCAC  CCATCACACG  GAATCGGTGT  TCTGACTACT  GGAACGGTCG  CCAGATATTC  GTTGTACCGT  TGATAACGCT  ACCGTAATCA  CCATTACCCG  CACCACTACG  ACAGGGGTTG  GTTTTGCTCC  CAGGTTTGTC  CGGGGCGTCT  GCTAATAGCG  GCCTGGCAGT  TGTCTAGTTA  CTAGTAGCAT  GGATACGTTT  GGAGTTACGC  GGCGTTAAGC  TTTATTGGTC  GTGGGCTCAA  CATCGGTACC  ACTGCGGCCC  CACCAGGCGC  CGTATAGCCG  TGGGGGGATG  AGGATTCTGC  ACTACTGTAG  TCCGACAGGC  AGTGCGGAGG  AATAGGATGA  AGGGCGACCC  GAGTTCGTCA  AAATCCGCAC  ACTATCAACT  GTCCCCCGTC  CCTTGCTACG  GTGGAGGGGG  TAATTCATCC  CTGAGAGCAT  AAGCAGTCAG  TCAGGC  TCGG  GCCGGATATC  GCATCGATGT  ATTCCGCATT  CTTGCTTCGC  GGGGTGTCTG  AAACATCTTG  CGCCCCCAGC  GACAGAACAT  TATTCAAGTG  GAAGCGGGCT  CCAACCAGAA  AGCAAACGGA  ACGAAGGGCC  AGCTATAGG  ACATATGT  12-15:  GTGGAATC  ATACTAAGCA  CCCTAGTTTA  AAGAGTACCG  CCGAAAACAT  TGTTGAGGAT  ACACTGCGAA  TGCTGATTGA  GACGGGAACC  TGCGACATAC  GGAACCAAGG  GATCTCTATT  AAAGCCGCTC  GCTACTGACT  AGATCCCGTA  GATGTTACGC  GACCTTAACT  CGCTGATAGG  GGATTCGCCG  TGGGCGTTGT  ACCACTGCGC  CGACTTCTCT  GCCGGCGCCG  CCTCGGGTAA  GTAACGGTTA  GTAAGTGCAG  TTGGTTTGGG  CCGCATTGAG  TGAGGTGCCT  GCATGGTTTG  ACTCTCATAT  GCCTTGGGAG  GACAAATTGA  TCCCAGCAGA  ACCAGATTTG  TAGGATGATA  GTTTGATAAA  CACGTGAACA  CTCCTCTATA  AGTGCGCTGA  GGGTGTCAAC  AGACTTGTAT  TAGGACCGGG  GGCACACATC  CGTTCATATG  GCGTGGACCT  AGCCCGAGGT  TTTAGGTTAG  TTACCCAACT  AAACGCCTCA  CATCTGATGA  TACTTACGCA  TTGCCTGACG  AGTTGCGAGT  TCTAGGCTAA  AATAAAGATG  TCGACAGTCG  GTGGGATAAC  ACTTTGGTGT  GAGCGGATAT  ATCAGAATGG  CGGGACCATC  TGGGATAAGC  CCTCATGTTG  GGACCTGGGC  TGTCGAGGCC  ACCTGCATGA  ACTGCAAGTT  TGACTACGTA  GGCATTTGCC  GCCCGTTTGA  ACCAAACCGG  CACTTACTAC  TTGCGAAAAA  AAACGAGTCC  GAACCCAGCA  TCGATCCGTT  GCTACGGTCG  AGTACTCAAT  AATGGCGCTA  AAATAGGTAC  CGGCATCGTA  GCCCCCTCGG  TTAGCAATTC  TGCAGTAATT  ATAATATGGC  AATTGAGGTT  GAACACTTGC  TATGCGGACC  TTTACGAAGT  TATGGCAGCG  TGCGGGTCAG  CTATTTTGGT  AATCGCCCGC  TGGTGTCTGA  CCGCTACACA  AACCGAATAC  CGCACAATAC  ACTGCCACAG  CACTACTATC  AGACTAAGA  AGGGGCAG

    13-15:  GAAATACA  CCGCGTTCGC  CTGTGCGTAA  GTCTAACAAG  GCCCCGCGAA  CAAACTATAT  CCAGAAGATA  GGTTCCCAGC  GTCTGCTAAC  GAATGTGTTT  TATTGACATA  CCAGGCAAGA  GCTACTCCCC  CTCAGGCCTA  TTGGGGTAAC  GATGATTCGC  CATTAGGCAC  CCGATGACTA  TCGTAGACGC  ACACCGTCGT  TCGTCTACTA  GGACAGTTTT  AAGATGCTCC  TTGGTACCAA  TTGTGCAATG  GGCTGAATCT  ACACTTCCTG  ATCATGGACG  CAAGTTATTC  CAATTAGACG  ATTGGTCGAA  ATCCTTCCAT  TGACGACCTA  AAGTGAATGC  GGGTACCTGT  ACGAACCTGT  CCCCCAGATC  AATAGGACGA  ACTCCGCGAG  ATACCTAAAC  CAAGTTGTCC  GCCGCGGCTC  TTGGAACCGG  GTTTTAGGTG  CGCCAATACG  TTCGCCGACA  GCGAGTTCTC  TTAGAGCAAA  GACAACAATG  CGTTGTGCAT  ACCGAGCCAA  GACTCCGAGG  ACCACGCGTG  CGTCAAAGGT  CAAGATAGAT  GCGACGTTTT  TGACGTCTAC  CAGAATCGTG  GAAAGACACA  TCCCGTGGCT  GTTCGCCCTA  GTTGATCGCC  TCCTGCATCA  TGGGATAATC  TCTTTCAGCA  CCACGCCGCC  GCTACACTAA  GCGCCTCACA  GCCTGAATAC  CCGTCTTTAA  GCTTTATATG  GTAAAATTAG  TAGGCTTTAG  ACTGCTTATT  GCGCGCCGCG  CCTCGCTGAA  CCACCGACAA  TTACTGCCGC  TGAGATCATT  TGTGTTACTT  GAACCCAAAC  ACAGAGAGGG  ATGCCAATGT  ACCTATAAGC  AGTGATCATT  ACGCATAGCA  GGTAACGAGG  ATACTGGACT  TCCCAATTCA  CACCCTTCAA  GCGTTGGCGT  GGGGGATGCG  GCCTATGCAG  GGCTGAAGTC  TGGAACCCAA  GAGAATTCCA  AAGGGTATTG  AATTGAGCGG  TCGCGATCAA  TAGTTTGTTA  TTCAGGCGC  AGGGGCAG

    14-16:  CGGCGGCA  ACCTACGCAT  CAATCCACCC  AGTGCCTATT  CGTACATGAC  AGTTATCGTT  TAAGATTCCG  ATAAGTACCC  ACATAGGGGG  GGTTTGCCGA  TACACGCCGG  TTGCTATCGT  CTAACATAAC  TGTAATAATT  GACCCCTCAG  TGAGCCGTAT  GCACGACTTC  GAACATTTTT  CGTGTTTTAG  GTTTTGTCAC  GACACGAAAA  CCTGCAGAAC  CACATGGTGG  CAGAGCTTGC  ATACACCCCT  TGATGGGAAA  GGACTCTAGC  TCTTTATCTT  GCTACGGCAC  GATTCCCGTT  TACCGTAGAT  TTAGACCGCT  TGACCTTGAG  TTCCTTGATT  TAGCAGGTGA  ATCCATGCGA  AACCCATGCA  CGATTCCGTT  CGTATCCCTA  TATTTGTGTT  ATGACACAAG  TTACTCAGTT  GTCGGGGATA  CCGGATATCG  AAGACACGAA  AATCGTAGGC  CTTCGTTTTC  TGCTGACTTG  TGAGCATGGC  AGACCACAGT  GAGGAGTGCC  ATCCATAC

    15-18:  TATGGAAC  TGACCTAGCA  CTTCGTTGTC  GTTAGCACGA  GGGCTGGTCC  CCTATTTTGA  GCGACCGTGC  GGCATGCGAA  GAGACCTCAA  GGGGTAGTTC  GAAACGGCTT  TAAGTTGAGT  CTGGATTTGT  TCCTCGGTAA  TGTGACCGGG  TTTATCATCG  GTTTTACCGG  ATTAGAGTTA  ATGAAGAGCC  AGTTCAAACC  TGCTTTCACG  AAAGTGTGGG  AGGGCGCTAG  AGAATAAAAG  CCCTGAGTAT  AGCCTTCGCG  CGAAATTAGT  TGCACCACTC  GTCTACGCCA  TTTCAACAGA  TTAGGATCGT  ATCCTTTAAT  GGGGGATGGA  GGTTTCATTC  ACCGTTTTGC  AAATGGCGGT  CCGG  CTCGCTGA

    16-21  TGAGCCGC  AACGACATAG  CAGAAATTAA  CCCCCTTAAA  CGGCAAAACG  AGAGAGCATT  TTTTAAGTAC  GAGCACGTAT  TGTTATACTG  TTAACGACTA  AAGGCAGAGC  ATCGTGCTCC  ACTAGTCATA  GGGTGCCAGT  GTTCACACCA  CTC  GTGTGCA  TTAAACGTCG  CGAGATAATC  CAGACTAGCA  GTGTAAGCAG  AGCCACGCTA  GGGGCGGGTT  CCGCGGTGAA  GCGCTACCAG  GTCGACCTGT  CTACGAAAAT  AAGTAGAATG  GTGTGTCGTA  TAAGACCATT  TTGTAGAACG  CCGGGAACGA  AGGACAGCGA  CAGAGGGGTA  TGCTACGTTA  ACTGCATTGG  TATCGGAACC  TGAG  TTACGTGT  16-22:  TGAGCCGC  TAGTAGAACA  TGCCCTAAGC  TATGCATGCG  CGCCAATGCG  GCGACGGAAA  CCACGTCGCC  AGCTCAATAG  AGAAAACCGT  CCTCCGCC  ATCTGACA

    17-22:  CGGCGTTA  GAAGAATAGG  GCTTATTCGC  GGAGGGACGC  TGGGATACCG  TTGCGGGTAG  CGGTTACGCC  TACA  ACAACA  CATCTTGAAG  TGGGATGGCT  TGATGAGCGC  TGGTGAAATT  GTTTAGTA  ATCTGACA  17-23:  CGGCGTTA  GGTGGAATGA  GGTTTTTTGA  GTAAGTCGTA  CAGTGCCCTA  GCGTTCGGCG  TACGCCCGTT  CAGCCACCAA  CCAACTTTAC  GGACCTCCAA  ACTAGCAGCG  TGGTCTTCAC  GTT  AGATGGCG

    18-23:  AGGACCCA  GGTGGCGATG  ATCCCCCTAT  CCGCAGAACT  CTCGCGCTTA  AGACAGTCGA  TTGGGCAGCA  CAAA  GTCAGG  TCGACTAAAT  CCGCGGCGGC  ACCAACATAA  GGAATTAAAA  ATTTGCATGG  TTCGGTATTA  GGAATACCTA  CATGATGAGT  AA  AGATGGCG

    19-21:  ACGCCTCA  AAATCTAACG  CCATTCGGGG  TAATCGAAGC  CGAAAGACAA  TCAGCACCAA  TCGGCAAAAA  GTTG  ATCCCT  CAAACATACG  AGCTGTGGAA  ACGACTAAGG  CGGTGCCCCG  ATGGCATACT  CCTCTTTAGA  AGGTAAACGT  TGAGCTAGCC  TCGTTGGGAT  TTGCCGTTTT  TAAAAGGGGA  GACTGTGTAC  CAGTTTAACT  CGTTGGTCGT  AGTACTCCAT  CCTCGGGGCA  TCTTCCATGT  GTGAGAATAT  GGAGGAATGA  GAGTACTAGG  TCACTTTGGG  AAGCAGCACC  CTACAGAAGA  GTCGATCGGC  TCTGGACATA  TTGTTGTGAA  TAT  TTACGTGT  19-24  ACGCCTCA  GTCGACACTG  CGTCTGAACG  GGTTCTGGCC  ACCACCGAAT  CATTTTAATA  AGCACACTCC  ACCTGCGAAG  TATCGATGCC  CACCAGCTAG  AACGACTCGC  ATCAGTGAGT  GTAGGGCCGC  ACCGACCGAG  TGGAAGTTCA  GGCAGCTTTG  CACCAAATCC  CCTCCCCTGA  CTGCGGCAGT  CGAG  CGCGTC  ACCAGCTACC  CATTTATATA  AGCAGGGAGA  CGATTATATG  CGGATTCTCA  TAATGCGACT  TCCCCCGTAC  ACCCTCGGAG  ATAGGATCGG  AGACTTGGGA  AGCGTAGTCG  TCTACAATAG  ACGTTGTACA  TGGTCGTCCG  TTGAAGAGGA  TA  AACAATCC  CTATACCTTA  CTTGGCCAAA  TGCGTTCATT  GCGGGCCAAT  TCGCGACCGA  GCAAATAAGT  AGTGGAATGA  TCTCGTCCCG  GTATTATCCC  AGCCTAGCTT  CCGTCTAGAA  CGATTTGTTA  GGTTCAACGT  TAGTTCGCTA  GTAGGTTATA  TTACTTGT  19-25:  ACGCCTCA  TCGGCCCTTT  GCGTACCGAA  ACCTCCCGTT  TTAATCTCGC  AGTTCGGCCC  GCGAAGGACA  TCCTTCCCGG  GGGTTCTATA  GAACCTCATC  AAGAACCGGC  TCTGTGTAAG  TCTCCTTGGT  CTGGGCGACG  AGTTACGGGT  TGGCTTATGT  CCGGTATACA  AAAGTCTCCG  ATGATGAGTC  TTCCCTTGGT  AGTAACTCCA  TTCGGGGTCT  ACCGTCGGTC  ACAGCTATAT  TGGCATTAGT  TACGATCTCA  CATGTCGCGT  TCGTACGTTC  AATATGGCGG  ATCGAAGTAT  TGCACCTTAC  CGCAGACAGC  GCAGGCAGAA  GGGACATTGC  CAATATACGC  CACAATAGGC  AATA  AGACGTAT

    20-22:  TGGGAGTC  ACAACGCCTC  GAAAGTGGTA  TTTCCAGTTG  TTACGGAGCT  TCGGTAGTAA  AAGGGGTGGC  CTGCTCAAGG  TGACCCATGC  GTTTATACGG  AACAAGGACC  AATGGTTAAA  CAATGGGCCA  GACGTGTATT  TCGCGATTGT  CCTAGAAGAG  GGAGCCA  ATCTGACA  20-23:  TGGGAGTC  CTTACACCCC  CTCTACTACT  CGGCTGAACA  GCTATTCGGG  AGGTGCATGA  AGGAATCCAC  TTTGGATAAG  TCCGGACCCC  CCGACAAGGC  TGGTTCCACG  CTACATGCGC  TGACGTTCTT  ATAGCATTTC  GGCTACTGAA  GGA  AGATGGCG  20-26:  TGGGAGTC  AGGTGCGCGG  ACAGATGGAG  ATTTTGGCAC  TGCCGTACCT  ACTGCAGCCC  CGTGTGCCAG  AACTATTTTA  TTGCGCAATC  AGATATTACA  ATTTAACGGG  GCGAAGGAGG  GTTCTTTCCC  CCAAAAGTGG  ACGAGATGAT  TGAATTCTTA  GGCTCCATCG  GACGACACTC  TTGACGCATA  TGAACGCCTG  TAGAAGAGAC  TCGCAACA

    21-22:  CTCAAATT  CCAACGACAT  TAGGGTAATA  TCCAATACTC  TCATCGT  ATCTGACA  21-24:  CTCAAATT  TTTGGTAA  AG  GCACCACCGG  GACGTGAGAG  TCCCCGAAAT  AGAAGCTTGT  TGTGGTGGGA  TCCCTGCCCC  GTGAGTATTG  TGGCGAACTC  GGCCTATGTG  CTAGTACGCT  TGTATCCCAG  AGGGTTCCTT  AACTGCCCAC  TTGGAATGCC  GAGCGAACCC  CCTTATCTCC  TGGATTGAGG  AAACATCACA  GGCATTGCGG  GATAGGGTGA  GATCAAGCGA  TCCTTATGCG  AGCCCA  TTACTTG  T  21-25:  CTCAAATT  AGGTACTCGG  TTCTGACTTG  GTAATAGCAT  CGTACAATTT  AGGTGGGAGA  CAGTGGAGCT  GTCTTTG  CGC  GAGAGGGTGT  TGT  AGACGTAT  21-26:  CTCAAATT  CAAGATCACG  AAGTCCATGT  TTAAATCCCA  TTCCCTCTAG  TTGC  GCACTA  AGCAAAAACA  GGCAAAGGCT  CAGCAAGACG  AGATTGTCGC  TCTG  TCGCAACA

    22-23: CATTTAGC TGGAATAAAT ATGTAT AGATGGCG 22-25: CATTTAGC TGAGGATCAT AGCGGCACCC AAGAAAGAAT AAGGAATGA AGACGTAT 22-26: CATTTAGC TGGGCTGAAC TGTGCGTTCT CG TCGCAACA

    23-26: GCAGGAAC GACGTGGATG GAGTGCGACA CTTCGTTGAT CAGTTATTCG TCGCAACA

    24-25: AATCACCG CGCGGCTATG GATTGTGGGT AGAAATAAGA AGTTGCCACG GGCATCAACC AATACTCCTC AAGGACAATT TCGGGTCGTA GCTCTTGGTA TAGCTGACGA ACTAACCGTG TATCCCACGT AAAAG AGACGTAT

    25-26: GCGGGGCA ATATAAGGAT GTGGGTAGCA CCAAAGACCG CAACTTGCAA CGCCTCCCTC TCGCAACA

    Next we present coding for Subgraph II.

    VERTEX CODING: 1. GTTTTACC TGGACAAT 2. CGCGTAAT CACACCCA 3. TAATGAGG ACCTGGCC 4. ATTACGGA ATAGCTAA 5. TCAAAACG CGTGCGTG 6. TGTTTATG TGTTTACT 7. TTTGACCT CGTAGCTG 8. TACCACGT GGATGAGG 9. GGTGTCGC CCAGCTTT 10. TAAACGGT GCACCTCC 11GGGAGCAT AGCCATTA

    Finally the edge coding for Subgraph II.

    EDGE CODING: 1-2:  ACCTGTTA  ACTGGAAACA  TCATGGGTCC  AGTCCCCACG  GGACAGAACC  GAGGGACGGT  ATGAAGTTTC  GCCAAGACGA  GTCTTGCATC  AGCTGATCTT  GTAATGTTGA  CCTATGTTAT  GGGTCCATGG  ATCACTACGA  CCCCGAAGTG  GA  TTTGTTTT  TGTGGCGTGC  CGGTGTA  GCGCATTA  1-3:  ACCTGTTA  TTGCGAACTT  GGAATACGTC  AATGTCTACG  GGCATTGGTA  ACTGTTAGCG  CACCGTCCGC  GACAGCAGCA  TACGGGTGG  ATTACTCC  1-4:  ACCTGTTA  GGGTTCGAAT  ACCCCTATGT  AGTCATGAAT  CGTTTATCTA  TTGTACCCTG  AGTACGTATG  GTAAAAC  TAATGCCT  1-5:  ACCTGTTA  GGGTCGGTCA  GAAGGTTTTT  GTTTGCTGGT  TCTGCCGCGT  GCCCCCGTTG  TTATACACAC  TGGTGGACGC  ATGTGCGCAT  GAATGTTCAG  CAGA  AGTTTTGC

    2-4:  GCGCATTA  TGGATAACGC  GACTGTAGGA  GCTGCAGGTT  GACACGTTCT  TACGGCTGCA  CATATACTTA  CCCTTTT  CTC  TAGAAGGCTA  GAAATAGCTC  CGTTAGCGCC  GTCTCGTCAC  GTAGTAACGA  TGTCCGCATC  TTAAACGCAT  T  TAATGCCT  2-5:  GCGCATTA  CATACCGATA  CGGTCAAATC  TGGCAGATGG  CCGGCTCATA  TCCTGAGGCC  GCTCGAGCAT  CCCACGCACA  ATTGTGACCG  AACGGCGTTC  CCACGGCGAT  AGTTTTGC  2-6:  GCGCATTA  GTGACACGCG  AATAGGAAGA  GGGCACCTTA  CTGCGGCTTG  GACAAGTCGT  GACTCGTAAT  GTTCTAATAA  CCTAATTTTC  CTCATGAGTG  AGTTGCTGTT  ATAAAACTTA  CCGAATAGAA  GCTATGTGCT  GGGAACGGCG  TGAGTATAGA  GACCACTTTC  CGGCGCATAC  GTCCGCCGCG  CTATTTATTC  ACCGAAGACA  CGGGGCATTT  AGCCCGGAAT  AACGCGATGA  CAGGATAGTG  TATGGGCTCT  CACATTGCAT  CGCAATGTTC  ACATCGCGTG  TCCCGTCAAG  TAGGGTGCGA  ACGCCATAAA  CGGCTGACAC  ATACCCGGTA  CTAGATCACC  GATTCATACT  AGCT  ACAAATAC  2-7:  GCGCATTA  ATCCGCAAGA  ACGTAAGTCG  AGATTGAGCG  TAGATAACAC  CGCAACGATT  CGGCTGTTAC  AACTTAGGAC  AGTTTCTGGT  TTCCAAGTAT  TGTGCTCAGG  TCATCGGATG   GGACAGTCCT  GGCGTCGAGG  CACCTGGTTT  CCTGCTGATC  GACATAACGT  GACTTGCTGA  TGGGCTAAAA  TCAGTACCAA  GTACAAATGA  TGCCAAAAAC  GATTCAGTCA  CTATGCCTTG  AAGCATTACG  CCCCCGAACG  GGGTACAGAG  ACCTCGGACA  AGTGTTACAC  GTCCAGTCCT  GCGGGGACGT  CAGTCTAGGG  GCCCCTTCAG  GCTTCGACCG  TACTCAGTGA  GATGAACTCA  ACTGAA  TTTG  TATTCCCCGC  TAGTCGCTAT  GGCGAGACTA  GTAGGTTCCT  CTGGCCATAC  GTCGATACTA  AGCATAGGAA  TCAAACCCGC  CGCCTACGCT  CGGTATGCAA  GAACCCGCAG  CTCTATGAAC  AAGCTCAAAG  CCTGAGCGGC  AAACTGGA

    3-4:  TGGACCGG  GCAAATCTCA  CCAACTTGAC  TTACATTGCT  GGG  TAATGCCT  3-10:  TGGACCGG  GATTGAAACA  TTTAGTGACT  AACGGCGTTC  GTCTTCATCT  AAGACTCAGG  TGTGTGTAGC  AAGTTACTGC  GTTTGAACGG  CGGAAACCAA  CAGCTGAACG  TGTGTTTTGA  ATGGTTCGCG  ATATCACCCT  TCCACAGTGA  TCCCTTTTTG  ACGAGTGGAC  GGTACCC  ATT  TGCCA

    4-5:  TATCGATT  GGAAGTCGTG  GGCAGGTTCT  CCATAGGATC  CTTAATGAGG  AGTTTTGC

    5-6:  GCACGCAC  AGCCTTTAAC  CATCAAGTAA  AGAACAGTGG  CGTCATGGCC  GGCGGCTGGG  TGTCCATGAG  TTCGTACCGT  GCTAGTAAAA  AATCCTCGCG  CCATGCACGT  ACAAATAC  5-7:  GCACGCAC  TCTTATCAAT  CAGAAGGGTT  GGGCTGTGGC  TCAATTAATC  AATAACGTTG  CTATCACCTG  AGCCATTCTA  AATGTGAACC  AGGTCGCTAG  CTAGATCCTG  CCTCATGTAG  CATTTACACC  CCTAACAGCA  TAGCCCGCTG  TCGGGTGACG  ACGGCCGTAA  ACGCGTGCCA  AGAACGGTAG  GCT  AAACTGGA

    6-7:  ACAAATGA  CCTGGGCGTC  TTCGGCATAA  CAGCGGGGAG  CGCATACTAT  TGAGGGTACA  ATCAGGATCC  TTTCTGGTTT  TCTCCGAGTC  CCCTGGTGCC  GTGGTCCCGC  ACGGGGGTAG  TGCCGGAATG  TCGCATAGGA  ACGTCAGTAT  CTGGG  ACCGC  CCCTAGGTCG  GTGAGTCCAC  CGTGTATCGA  GTGACCAACC  AGGCCCTTTT  TACTAAACGG  GTGACATTGT  TGCCAGATAC  CTTCATGTTG  GGTTCAGCGC  AAGCGGCGTA  ATTGCAAATG  TTGCCAGATC  AATCTAAGAT  CACGTAGTGA  GTACG  TCCAG  CTCTAGAGCT  ACCCTTCGGC  TCTAGGAGCA  CGTTGGACGC  AGGCCGGAAT  TACGCTATTA  ACCTTGTCGT  CCTCCAATTA  CGAGCACCTC  TCAAGGCTGA  GTCGTCAGGA  GGTGCGCTTT  CCCTGGCTAC  TGTGTCGGCT  CGCTGAGCTT  GTCTATTCGC  CTGACTAAGC  CCCCGTCTAA  CTCAATATGG  AAACTGGA  6-8:  ACAAATGA  GGAGCCAACC  CGTATCAGGT  TGAGATGTGG  TATACTTACG  GCTGCACTCG  TAGTTCCTAA  GTATACTCGC  TAACTTTGTC  TCACGGAATC  CACTTTGCCG  AAGGAATATG  CCTTGTAAGA  CTCCCTTATA  TTGAAGGGTA  GAGAAGATTC  TTCTCAGGAT  AACCCGGAGG  TACAACGCAT  CGGTCGGCAA  CCTAGGGGTC  GACGACTTAC  TACCGCTGGT  ATCCTCTGCG  CGTGGAATGG  TAGCCCCTCG  GCCGGCATAA  GCAGACTACG  GCAAACGGTA  ACGTTCTACT  TCGGGCGGAT  GTCCATTGGA  GCCATTTAGG  CTAGAAAGGG  CCCAGCTTTA  GATAGAACCC  GTTGCATATG  ACCTTCTCCT  TCTAACGAAA  TCTAAGGTTC  ACGGGCCCCC  CCTCAGCGAA  CATGTCCCGC  CATTACTACA  AGAGGCATGT  TCGCAAGATC  CAATTATTGG  TGTTAACCTG  GATTGGTGCC  TAATGTATGT  GGCCGATTTA  CTTCGTTTCT  TGCTTGCTGA  GTGTGGTCCC  CCCCGACTTC  CGCGCGAAGT  CAGATATCAA  CATACGGCCC  CCTGTGCCAC  CACTGGTGAC  GTAATTAGAG  GTCTAAGACT  TTTGTGTTAC  GCTCTCAGTT  AGGGCCGACG  CGGCATTTAA  ACTTGGGAGG  ATCGACGCAT  CTATATCTGG  CTCCTAATAC  CATATTAGAA  TACACAG  ATGGTGCA  6-11:  ACAAATGA  TCACGCAAGG  CAACCACGGA  CCCAAATTGC  GAACCACCTC  TGGCGAAGAC  AAACATACAC  AATAATTCCA  TTCGCATGAA  ACCCGAGCTT  CGCGCCGAAT  TAGCTGTAAG  AGCAAAAATA  ACGCAGGCAG  AGGGCGTGTA  CCGGGGGCGT  CCGAATTCTG  GAGGCAGAAG  TAGAGGTATG  TCGAAAATCC  ATTACCTCCG  TATATTCACT  TCCAAATAAA  TAAGGAATCT  AAAACTCGCA  CCACGTGCTT  TTTAGGTCTA  CATATGTGGG  CCGCCGAACG  ACCTGGTTCG  TAGAATCGAA  GTCGTCGCAG  CAAAGACGCT  CTGTT  CGGGA  ATGGTAGCAG  GCCCTTTATA  CGGTACTTTT  ACTTAGGGGG  ATATTGGCCG  AGATGAGGTC  CTGGCTTAGC  ACCCCTAAAA  GCAAACACGT  GGCGGAAGAC  AGCAAACAGG  GGGGTCCCAG  TGAGATCCCG  GGACTGCGTT  AAGCGGGTCC  CGGACTATCA  ATCTAGTAAC  CCCTCGTA

    7-8:  GCATCGAC  GTTGTTTGCC  AGCCGGAAAT  CAAGGCAAAA  AAGTTAGAGC  CTGTATGTCA  GTGTTATTCG  TTATAT  CTGC  CTAAGCTTTT  CTCCTTCGTA  TGTCAAGATC  CGAATAACCA  AATGATTTAC  TAAGTCTTCG  CCGTTCTAAC  ATGCTCCGCT  TGACGTGAAC  TTAGGCGTCG  AACGAGTTGG  CGACAGAGTG  GATGGTTACT  ATCAGTGTGT  AGTCGTCGCC  CCGTAGGACC  CCATCATCAA  TCCTCCCCTC  GCGTAGCGAA  CGCACCGTCG  GGGAACGGGG  ATTGCGGAAG  CTTGCAGCCT  AAATGCATCT  AGGCCATTCA  CGAAAGATGG  GGAGATGTAA  ATGGCCTCAA  CACAGTACCT  GCATTGTGCT  AAGGCAAATC  GTCATTGGAA  TACTCGTAAA  GGCTAACGAC  AGTGAGCAAC  AAGGATTTTA  TCGGACCTTT  GTGCTGTGAC  AATCTGAACG  TTTCAAGCAA  GAACGTAGGC  GCGTCATGGA  TTAGGTCCGA  CTGTTCTATC  GTACGCCGAT  GTGAGTGGAA  TTACGCCAGG  ATGGCAGGCG  CGAGCCGAAT  TACTCGTTAC  GCGATCCGTC  CCAAATTGAT  TGAATAACCT  GCATGTAGAC  CCACGTCCTC  TCGGCAAGCC  TGTTACGTGT  TATATCTTTC  TTTTCAGCAT  CCTAGACAGA  TCGTTAACCG  TATAGGGATA  CTACAAACTC  TGATTCATCA  AGACCGATGA  AGTTGCTATC  CCACGTTGCA  CATATAAAGA  GTTTCAAAGA  GGCCCAACCT  CTTCCTCCGT  ATTCGCGCCA  GTAACGGTCG  TTTTACGCCG  AATGTAATAT  TGTCCGCGCT  CCTACCACGG  GTTTTACTCA  AATCGAGCAC  CGACTACGTC  AACAAAGCTA  ACTATGTGGA  TAATCATAGC  GACGCCCAAA  GATCATAGTA  TTAACTCCTT  AACTTTTTGC  GGTGTCTGAA  CACAATTGGG  ATACGACTAT  GGAGAGGCTC  GGAGCGGAAA  ACATAGCGG  ATGGTGCA  7-11:  GCATCGAC  CAATGCATAT  ACCTAACCTA  AGGCCGATAT  CCCGTCTGTT  CCTCAGCCCT  GGCTGACCTC  CGCCCTGCTG  GAGTTGCAAT  TGGCACTAAT  CCTTCATCGG  AGAGAAGCGG  CCCGGGTGTA  GTATAGATGC  GCTGCGAGTC  ACAGGCTGCC  CGTCGTAGAT  GACGATCTTA  TATATAGTCT  TTCAGTGAAC  GGTTCGCATG  TGAGTTAGAC  CCGTTTCAGC  GCGCGGCACA  TCAGTTTAGA  ATGGCGCCTT  TGGCTCGTAA  CCCAGGTTGA  GAGTATACTC  AGGTTTTACA  ATTCGACATC  TTAACTGATA  CGTGATGGAT  TGCCGCGCTG  TTTTCGTTAA  GCTCGATATT  TCACGACTCC  TATACTAGTT  CGAAATTCAA  TCACTGGGAA  GGGTACTGGG  CATTTCCTAT  TATACCTCTA  AGAAGTACGC  TAACAGGCGC  AAGTATTGGC  CTACAGACTT  TAGGCGCCTG  ATGACAAGCC  GACTCCCCGT  TTATTTAGGA  CGCAGAAGAG  TTAAGTCACT  TCCCCCTCAT  CTTAATAGTG  TATGATTGAC  ACTGAGCACT  TTACAGCGGT  TACCGAGTTA  GTGAGATACG  GGAATACTGC  TATCTTGGTG  GTCTCGGGCG  TTGACATGCC  ACCCCGACTA  TGACGAAAAA  CCATAGAAAC  TAAGGAAGCA  TGTTTTTTGG  GACGACGGCA  TCGTTGTGGC  TCCATATCGT  TCTTTCTGTA  GATAAGCTGA  GGCCCAGCGG  CACGGGGTAG  TTGGGGAGTA  ATCCCAGTTC  ACGTTACATC  GGTTCTCTGG  ACACGATTGC  CCTGGCGACG  ACAGCTCACA  AACTCTGGCT  TCAGAACGGG  CTACTCCCTT  CCGTAGTAAC  TTACGTTCCC  TCCGCGTGGG  CGAGCCGAAT  GAGTAGAATT  TTCCCCGTAG  ACAAAGCCTG  TGAGCTGGCT  TACAGTGACA  GGCTTTCGCT  ACTTGATGTA  CGATTCTTTT  AGGAGCCTCA  GTTCGGAGAG  TTAACTTAT  CCCTCGTA

    8-11:  CCTACTCC  TGAACAACCA  TCAGCGATAC  TAATTGGCGT  GTGTCTCGTA  TGAACACCTG  GCTCATCTAC  CTCTTT  GTTA  GAACTATAAT  AAGGTTCTGA  AATCTGTGTC  TTACGCTCCT  CGTCGCGGAT  TAGGCCGGAG  CAGAATCGGT  CGAATT  CAGA  TCATTTCGAT  ATATGACGAG  TCCTCCATGC  TACAAAGAGC  GCATGGGGCG  AAAATACCCG  ATAATACTTG  GGCCAATATG  GGCGCTGACT  AAAAGTTGAG  GTGGGACGCG  CCCCTTGATA  TAGCCCGACG  CGGATAAAAT  GCCTACCTAT  CTC  GCGAGCC  TACATGCCCG  TTTGGCGAAT  TTAACGCCAT  TTAAACTGAA  AAAACATAAC  AGCCCCGGTG  ACGGATGCTG  GA  ATCAAGGT  AAATACGCAA  TGCGAACAGA  TAGCCCTCAG  CATGACCGCA  GTGCGTACCC  CCCGAGTCCA  ATCCTGCTAT  TTATCGCTCA  GAGCACCGTC  GTCGGCTAAC  CACTCACTTG  TCAAAATCGC  AACACCGATA  TATCGTGCAA  CCTATACTCA  ATTCACACGG  TCGTTCGCGG  ACTCGCTGTT  GCCGGATTGC  GTGTGGGATG  CATCGGGTAC  TCAGGCTACG  TAAGGACAGT  GTTCTCCCTT  TCGGACCGCT  TTTAGAGACG  CTACAGCGGT  TTAGTTGGAA  GCACGGCCTC  CGACTCCGGA  CCCTTCTCAT  AGGAAGGTGT  TCTTTTACTT  CTAGAACTGA  ATAGGCAGCT  TAAAATTTAG  TTACAAGCAT  TTCGGAAATG  GCTACGTAAC  AGCACAGGAC  TTATACGGCG  CGGTAGTCGG  AAGTAACGCT  TTGGTCAAGG  CCCCACAAAA  GCAACCAAAC  CAGAAAAC  AG  GACGAGATAA  GTTTTTCCAT  CGAATGTAAC  GGAATGACCT  TAGTTCGCTT  AGGTGATGAT  CGCACGAGTC  TACGATAGTA  TGGTGGGTAC  CACGGCCGGC  TACTCAGGCC  CCGCACGGCG  GAGTGGATGT  CATCAATGA  CCCTCGTA

    9-10:  GGTCGAAA  AAAAGTGTCG  GCATCGTCCT  AGCAAACAGG  CCTACTCGTG  TTTTACGTCC  AAAGGAAACG  CACT  GGACAT  AGAAAGTGCT  CCTTTTACGA  GACATGCGTG  TCTTCCCACG  ATAGTCCCGC  GGGAAGCTCA  CGGAACTTAG  GGTCTGTAAC  AAATTCCGTA  ACTCGGCTAC  CCGAGGACAC  GATTTACGAG  GGGCGGTGGC  CGGGGAAATA  GCCCCACCAC  GGCCGGGGAC  CGGGTTAGTA  CTCGTGGCGA  GGGAAGGGCT  CCAAAAGCCG  TCGATCGCAC  GATTCCGTCG  GTCCGAGTCG  CAGAAGGAGA  CCAGACAGTC  AGCGGCCGTA  CCCAGAATGG  CCAAAGCAAA  GCCTAATTGC  AGCACTGAAA  GTAGCGGCGC  GCCACCTGTT  GGGGGATCTT  ATTTCCTGTT  GTCTGTCCTC  GGAAATCAGA  TTATGGAAAT  CAGCATTATT  CAAACACTTG  CCTCAAGTGG  ACACGGTGTA  TCTCTCATCA  TGACCGAAAA  CGGGCTTTTA  TACGTACATG  CATATCGCGT  ACCCACATTT  GACGTAGTAC  TCGTCTTCAA  TTCGTGGTTC  GACTTGTAAG  CCAGGCAGAG  CCGCACCCTG  GGTGTCAGTT  TGCTGAAACT  GGCCACTGCT  AGCATATGCA  CGAGCTTGTA  TCTTCTCTCA  ACCACCGGTG  CCGCGGGGAG  CAACGGGGA  T  CCTCGCTAAC  TCAAGGCAAT  TGCGGGGTGA  GGGCCAGGCG  TGACCTGGGT  AGAGAACACA  TTCACCAACA  GAGCGCACAT  CACATCATTA  TACTTGTTTG  TACTTCTTAA  AAAATTGCAC  GGCGCTCCCT  ACGTTAGTAT  CTAGTCTTGA  AATCTGTGGG  CAGGCGGGGT  GATCAACCGC  TTCTAACGGA  GCGAGATGCT  AAAAGCATGA  TTCACATTCT  AGGGCAGGAA  GGTATTGTTC  ATAGAACTCC  CTGGTCGTCG  AGAAAAGATG  TAACACTATC  TGATCAAGCG  ATGGATGAGC  GATGGTATC  ATT  TGCCA

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.