Journal of Atomic and Molecular Physics
Volume 2012, Issue 1 854693
Research Article
Open Access

Phase-Conjugate-State Pairs in Entangled States

Ryo Namiki, 

Corresponding Author

Ryo Namiki

Department of Physics, Graduate School of Science, Kyoto University, Kyoto 606-8502, Japan kyoto-u.ac.jp

Search for more papers by this author
First published: 08 November 2012
https://doi.org/10.1155/2012/854693
Academic Editor: Alan Migdall

Abstract

We consider the probability that a bipartite quantum state contains phase-conjugate-state (PCS) pairs and/or identical-state pairs as signatures of quantum entanglement. While the fraction of the PCS pairs directly indicates the property of a maximally entangled state, the fraction of the identical-state pairs negatively determines antisymmetric entangled states such as singlet states. We also consider the physical limits of these probabilities. This imposes fundamental restrictions on the pair appearance of the states with respect to the local access of the physical system. For continuous-variable system, we investigate similar relations by employing the pairs of phase-conjugate coherent states. We also address the role of the PCS pairs for quantum teleportation in both discrete-variable and continuous-variable systems.

1. Introduction

The spooky action induced by the entangled particles at a distance is an interesting starting point in studies of quantum entanglement [1–5]. For the singlet state, the spins are always antiparallel to each other independently of the measured spin angle. Another familiar example is the Einstein-Podolski-Rosen (EPR) state. For the EPR states, not only the positions of the two particles but also the momentums of the two particles have perfect correlation. When we consider the standard form of the maximally entangled state in two d-level (qudit) systems , an interesting property is the appearance of a phase-conjugate state |ψ*〉: = ∑n 〈ψ | n〉|n〉 when a subsystem is projected onto a local state |ψ〉, namely, for any state |ψ〉, we have the relation
()
An example with two spin systems is schematically shown in Figure 1. A natural question is whether this coherent appearance of the phase-conjugate-state (PCS) pairs {|ψ〉|ψ*〉} can be a signature of entanglement.
Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
The pair of phase-conjugate states in the Bloch sphere when the fixed basis is the Z basis with the parameterization |ψ〉 A = cos (θ/2) | 0〉+eiφcos (θ/2) | 1〉. In this representation the phase-conjugation changes the sign of the y-coordinate and the phase-conjugate state vector of the system B is given by |ψ*〉 B = cos (θ/2) | 0〉+e−iφcos (θ/2) | 1〉. The directions of the Bloch vectors are in the reflection relation with respect to the z-x plane. The maximally entangled state is a coherent superposition of these pairs and produces the phase-conjugate pairs associated with the local projection in any direction as described in (1).

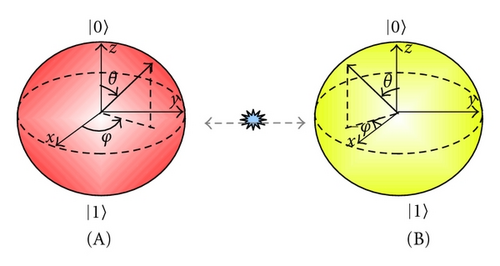
It has been known that the use of PCS pairs {|ψ〉|ψ*〉} is more efficient than the use of identical-state pairs, {|ψ〉|ψ〉}, in the transmission of unknown quantum states. Gisin and Popescu showed that the set of antiparallel spins stores the quantum information better than the set of parallel spins [6]. Zhou et al. provided a generalization of this relation by exploiting unknown PCS and identical-state pairs for two-qudit systems [7]. Similar relations have been found in the continuous variable system in which a set of phase-conjugate coherent-state pairs, say {|α〉|α*〉}, is employed [8]. Other insightful properties of the pairs of coherent states have been investigated from the aspect of the optimal cloning [9]. A scheme of continuous variable cloning of phase-conjugate coherent states is proposed in [10] and an experimental demonstration has been reported in [11].

In this paper we define the probabilities that PCS and/or identical-state pairs appear in bipartite quantum states. We investigate physical limits of these probabilities and their relations to quantum entanglement. In Section 2, we define the fraction of the PCS and/or identical-state pairs on a two-qudit system and investigate their properties. For the case of the uniform distribution, the fractions determine the symmetry of bipartite quantum states in the sense of [12]. It is shown that the fraction of the PCS pairs corresponds to the average fidelity of quantum teleportation. We consider similar relations with respect to two mutually unbiased bases in Section 2.5. We also consider the phase-conjugate pairs of coherent states for a two-mode continuous-variable system in Section 3. The results are summarized in Section 4.

2. Two-Qudit System

2.1. Phase-Conjugate-State Pairs in Two-Qudit States

Let us write a maximally entangled state (MES) in two-qudit (two d-level) system composed of subsystems A and B as . This state has an interesting property associated with a local projection (see Figure 1): if a subsystem A is projected onto a pure state ψ then the state of the other subsystem B becomes the phase conjugate of the pure state . In equation, we have the relation for any pure state ψ. Here, the factor comes from the probability that the subsystem A is in ψ, that is, Tr (A〈ψ| | Φ0,0〉〈Φ0,0| | ψ〉 A) = 1/d. Note that the phase conjugation is defined with respect to a fixed basis. Any maximally entangled state has the same property up to local unitary operation.

In order to find the role of entanglement in such phenomena, we may define the fraction of the PCS pairs by
()
where dψ is the uniform (Haar) measure which satisfies , and {dψ | ψ〉〈ψ|} corresponds to the positive operator valued measure (POVM) elements of the random projective measurement of a subsystem. The integrand implies the probability that a bipartite state contains the state pair |ψ〉|ψ*〉. Hence the fraction represents the probability that the local states of the system are in phase-conjugate relation. For the MES , the PCS pair appears for any outcome of the random measurement as in (1), and we have the unit probability
()
Now, we would like to ask two questions. (i) How high one can attain the probability of the pair appearance without entanglement? (ii) Does the unit probability f = 1 uniquely determine the MES? Is there another state that yields the pair appearance, unconditionally? In order to answer the question (i) we estimate the maximum value of the fraction under the constraint that the state is not entangled. We call a bipartite state classically correlated or separable if the state can be written in the form with the probability distribution pi ≥ 0 and ∑ pi = 1. If the state is not separable we call the state entangled. We define the classical limit fraction of the PCS pairs as the maximum value of the fraction f achieved by classically correlated states
()
where the maximization is taken over separable states .
Since any state being invariant under the unitary operation U ⊗ U* (isotropic state) can be decomposed into the form [13] we can write the isotropic operator in (2) as follows:
()
where we use (3) in order to calculate the corresponding term . Then, we have
()
The second term is the maximally entangled fraction achieved by separable states, which is known to be [13] (see Appendix A for a formal proof). This implies
()
From the definition of the classical limit fraction, any separable state must satisfy
()
and is a signature of entanglement (see Figure 2).
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
The probability of phase-conjugate-state-pair appearance f(ρ) defined in (2) must be no smaller than 1/(1 + d) where d is the dimension of each of the two subsystems. For separable states, 1/(1 + d) ≤ f ≤ 2/(1 + d) holds, and thus the state which satisfies f > 2/(1 + d) must be entangled. The probability of identical-state-pair appearance g(ρ) defined in (22) must be no larger than 2/(1 + d). For separable states, 1/(1 + d) ≤ g ≤ 2/(1 + d) holds, and thus the state which satisfies g < 1/(1 + d) must be entangled. This type of diagram was already presented in [12] where the maximally entangled fraction and the fraction of the flip operator are used to specify the conditions.
From (5), we can verify that
()
where the minimum is achieved by the states in the orthogonal subspace of . A notable feature is that there is no physical state that achieves the probability f smaller than 1/(d + 1). In other words, any bipartite state must contain PCS pairs with probability no smaller than 1/(d + 1). This is a sort of inequality to generally limit the capability of the physical process similar to the case of the optimal cloning [9]. It gives a physical limit on the probability that concerns the pair appearance of local states with respect to the local measurement. The physically possible regime and classically possible regime for f are summarized in Figure 2.

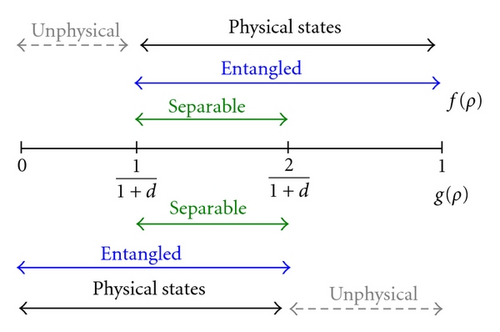
From (5), it is also clear that the MES maximizes the probability of the pair appearance and f = 1 uniquely determines . We thus have positive answers to the question (ii) and obtain the separable condition from the classical limit on the fraction of the PCS pairs associated with the question (i).

2.2. Phase-Conjugate-State Pairs and Average Fidelity of Quantum Teleportation

In this section we consider the process of quantum teleportation and show that the teleportation fidelity corresponds to the fraction of the PCS pairs introduced in the previous section (see (2)).

Let us define the generalized Pauli Z and X operators:
()
()
with |d〉: = |0〉 and ωd : = 2π/d. They satisfy
()
By using , , and MES , we define the Bell states as follows:
()
Note that 〈Φl,m | Φl′,m′〉 AB = δl,l′δm,m′, and the set of states {|Φl,m〉 AB} with (l, m)∈{0,1, 2, …, d − 1}, forms an orthonormal basis (Bell basis) on the two-qudit system. The process of the quantum teleportation [14] which transfers the state |ψin〉 in system A′ to system B by using a pre-shared entangled state is described by
()
where we defined the Kraus operator
()
which satisfies
()
If the shared entangled state is , we have
()
and the state on A′ is perfectly transferred into the state on B so that
()
If the shared resource is a maximally entangled state but not , we can redefine the local basis so that it becomes the standard form. Then, the teleportation procedure can be proceeded in the same manner.
For a given quantum channel Λ, we define the average fidelity as the probability that the state of the channel output corresponds to the state of the channel input averaged all over the input states [13],
()
For the teleportation channel of (14) the average fidelity becomes as follows:
()
where we used the relations such as
()
and changed the variable of the integration as in the last line. Then, we use ∑l,m  = d2 and (2) to reach the final expression.

Equation (20) shows that the teleportation fidelity is determined by the fraction of the PCS pairs. Hence, we can understand that the role of the entangled state in quantum teleportation is to generate the phase-conjugate state in a (remote) local system when the state of the other local system is projected onto a pure state. Note that the classical boundary of the fidelity achieved by the entanglement breaking channel [13] corresponds to the classical limit fraction of the PCS pairs defined in (4).

2.3. Identical-State Pairs in Two-Qudit States

In this section we consider the probability that a two-qudit state contains identical-state pairs {|ψ〉|ψ〉}. We show its physical limits and relation to entanglement.

The probability that a state contain an identical-state pair can be written by . We define the fraction of the identical-state pairs by
()
This is the probability that an identical-state pair appears subject to the random local measurement. It is defined parallel to the fraction of the PCS pairs of (2).
In order to see the property of g we give a diagonal expression of the operator ∫ dψ | ψ〉〈ψ | ⊗|ψ〉〈ψ|. Let us write the transposition of the second subsystem with respect to the fixed basis by Γ : (|l〉〈m | ⊗|j〉〈k|)→(|l〉〈m | ⊗|k〉〈j|). Since Γ(|ϕ〉〈ϕ | ⊗|ψ〉〈ψ|) = |ϕ〉〈ϕ | ⊗|ψ*〉〈ψ*| we can write from (5)
()
where we use (5) and is the flip operator defined as
()
The operator ∫ dψ | ψ〉〈ψ | ⊗|ψ〉〈ψ| is invariant under the unitary operations U ⊗ U [15]. The quantum state being invariant under these operations is called the Werner state, and such a state is characterized by the coefficients of the identity 〈1〉 and flip operators as the form of (23). We can see that the so-called singlet state with i ≠ j is the eigenstate of the flip operator belong to the eigenvalue ±1. The superscript (±) corresponds to the sign of the eigenvalue ±1, respectively. It is also clear that the product states {|j〉|j〉} are the eigenstates of belong to the eigenvalue 1. The set of the eigenstates {|j〉|j〉} and forms an orthonormal basis in the d2 space. Therefore, we have decompositions of the identity operator
()
and the flip operator:
()
From these relations and (23) we obtain a diagonal form of the Werner-type operator:
()
This expression implies , and we have
()
This relation is parallel to the relation on f in (9) as in Figure 2. Similar to the case of f, it gives another physical limitation: the probability of the identical-pair appearance cannot be higher than 2/(1 + d) for any physical state. As one can see from (27) the separable states {|j〉|j〉} can achieve the maximum of g = 2/(1 + d). Thereby, any higher value of the identical-state-pair fraction cannot be a signature of entanglement different from the case of the PCS-pair fraction.
Next, we determine the minimum value of the fraction attained by separable states. Since the expectation value of a partial transposed operator for a product state corresponds to a expectation value of the original operator for another product state [16], we have . Using this relation we obtain
()
where we use (9). This implies that the state is entangled if
()
From (27) we can see that the left equality g = 0 is achieved by with j ≠ k. For such states, there is no possibility of the identical-state-pair appearance.
To show a physical meaning of the identical-pair appearance, let us consider the following quantity:
()
Since the operator 1d−|ψ〉〈ψ| filters out the state ψ, the fraction of the orthonormal pairs |ψ〉|ψ⊥〉 contributes to this quantity (and reduces the value of g). Hence, the identical-pair appearance g negatively quantifies the appearance of orthogonal-state pairs. The appearance of orthogonal-state pairs is characteristics of the singlet state in which the local states are antiparallel to each other as mentioned in the introduction. Our result implies that such a phenomena cannot occur for the case of separable states and is a signature of entanglement.

Note that the unconditional appearance (the appearance with unit probability) of the orthogonal pairs is the unique property of the states in the antisymmetric subspace. This can be proven as follows: the condition g = 0 implies Tr ρ(|ψ〉〈ψ | ) ⊗2 = 0 for any state |ψ〉 since |ψ〉〈ψ | ≥ 0. Suppose that ψ is a “qubit” state so that |ψ〉 ⊗2 = (α | i〉+β | j〉)(α | i〉+β | j〉) with |α|2+|β|2 = 1. Then, the condition Tr ρ(|ψ〉〈ψ | ) ⊗2 = 0 for any α and β yields that ρ is the singlet state . Since this relation must hold for any choice of i and j, the states have to be in the antisymmetric subspace spanned by the singlets .

2.4. Summary of the Statements for the Uniform Average over the d-Level Local States

Here, we summarize the main statements in Sections 2.1, 2.2, and 2.3. We have defined the fraction of the PCS pairs (see (2)) and the fraction of the identical-state pairs (see (22)) in bipartite quantum states. We have shown that, for the probability f, the following statements hold (see also Figure 2).
  • (i)

    for any bipartite state .

  • (ii)

      is entangled if  .

  • (iii)

      iff  .

  • (iv)

      corresponds to the teleportation fidelity.

We have shown that, for the probability g, the following statements hold (see also Figure 2).
  • (i)

     for any bipartite state .

  • (ii)

      is entangled if .

  • (iii)

      is in antisymmetric subspace iff .

2.5. Two Mutually Unbiased Bases

In the previous sections the pair appearances are considered with respect to the uniform distribution that includes arbitrary PCS/identical-state pairs. In this section we consider the appearance of the PCS pairs with respect to the elements of two mutually unbiased bases.

The two orthonormal bases of a d-level system, say {|j〉} and , are said to be mutually unbiased if they satisfy the relation for any k and j [17]. Here we use a fixed Z basis {|j〉} and its Fourier basis defined by with . We refer to as the X basis since they are eigenstates of defined in (11). By definition, the elements of the Z basis are unchanged under the phase conjugation |j*〉 = |j〉 whereas the elements of the X basis changes under the phase conjugation as .

Suppose that the subsystem A is randomly measured on either the X basis or the Z basis. We are interested in the probability that the state of the subsystem B is the phase-conjugate state. Let us define the positive operator as follows.
()
The partial trace of this operator corresponds to the POVM of the random measurement of the two mutually unbiased bases (it satisfies the condition for the POVM on a local system ). We define the fraction of the PCS pair with respect to two mutually unbiased bases as follows:
()
Using the completeness of the Bell basis of (13) we have
()
From this expression we can verify 0 ≤ fm ≤ 1, where the maximum is achieved by and the minimum is achieved by any of in the last summation. Hence we could not find the physical limitation on the appearance of PCS pairs with respect to the mutually unbiased bases.
Since the last term in (34) satisfies we have . Using this relation and [13] we obtain
()
The equality is achieved by the state |0,0〉. Equality in (35) gives the classical limit of fm. Consequently, we have the inseparable condition [18] associated with the PCS-pair appearance with respect to the two mutually unbiased bases: is entangled if
()
Next, we consider the lower bound of fm for classically correlated states. Interestingly, we can find that fm = 0 is achieved by separable states when the dimension d is not a prime number. For the separable state we have
()
Suppose that d = pq with integers p ≥ 2 and q ≥ 2, that is, d is not a prime number. Then we can verify is achieved by the separable state |ϕ〉|φ〉 with and . Thus, fm = 0 is achieved by a separable state if d is not a prime number. This implies that can be achieved by separable states. Hence, a smaller value of the fraction of the identical-state pairs, which can be defined by , cannot be a signature of entanglement when d is not a prime number in contrast to the case of g in Section 2.3.

Let us consider some cases of prime numbers. For d = 2 we have and min ρ∈Sep.  fm(ρ) = (1/2)(1 − 1/d) = 1/4. The equality is achieved by |0,1〉. Therefore we obtain another inseparable inequality for the regime of smaller fm: is entangled if . Note that, in the case of d = 2, we have and , and there is no difference between the fraction of PCS pairs and the fraction of identical state pairs. This gives a different structure from f and g in the diagram of Figure 2.

For d = 3, it is found that , and a numerical calculation suggests that this value is the lower bound. For d ≥ 5, an upper bound of is given by the minimum eigenvalue of the (d + 1)/2 × (d + 1)/2 matrix:
()
The minimum eigenvalue of M corresponds to a minimum of achieved by the separable state of the following form: . Figure 3 shows the minimum eigenvalues for the first 20th prime numbers. For d ≥ 5, it is observed that is at least smaller than d−2. Unfortunately, we could not have found nontrivial lower bound on this minimization problem for the prime dimensions d ≥ 5. However, it is likely that there is a such lower bound to give a separable condition for each prime number of d and that a smaller value of the identical-state-pair fraction becomes a signature of entanglement when we employ two mutually unbiased bases for the prime dimensions.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
The upper bounds of for the case that the dimension d is a prime number between 2 and 100. The solid line is the curve of d−2 for a reference. It indicates that decreases much faster than d−2.

3. Two-Mode Continuous-Variable System

In the following sections we will consider continuous-variable analog of the pair appearance of phase-conjugate states. The analysis in Sections 3.1 and 3.2 is continuous-variable counterpart of the analysis on the two-qudit system described in Sections 2.1 and 2.2.

3.1. Conjugate-State Pairs on Continuous-Variable Systems

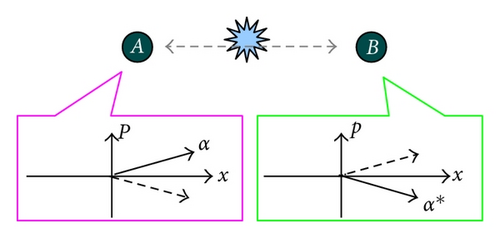
The EPR state is defined as a simultaneous eigenstate of the relative position and total momentum of a two-particle system. The EPR state thus has strong correlation on the positions and strong anticorrelation on the momentums. This suggests that the complex amplitudes of the two particles maintain the complex conjugate relation as in Figure 4. To be concrete, let us consider the form of the EPR state |EPR〉 = ∫  | x〉|x〉dx = ∫  | p〉| − p〉dp [1]. Here, |x〉 and are the eigenkets of the canonical operators and belong to the eigenvalues x and p, respectively. Here and in what follows we assume the commutation relations for canonical operators . We can verify and . We can also rewrite this state in the coherent state basis by using the over completeness relation π−1∫  | α〉〈α | d2α = 1 as |EPR〉 = π−1∫  | α〉|α*〉d2α. This expression demonstrates the pair appearance of the complex conjugate coherent states, {|α〉|α*〉}.

Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
If one of the EPR particles is projected onto a coherent state |α〉, the other particle turns out to be in the conjugate state |α*〉. This is a continuous-variable analog of the phase-conjugate-pair appearance of Figure 1.
As an experimental implementation of the EPR state in the quantum optics, we usually work with the two-mode-squeezed states (TMSS):
()
where |ζ|2 < 1 and we use the number states {|n〉} as the fixed basis. The TMSS is a simultaneous eigenstate of
()
where (, ) and (, ) are the annihilation and creation operators of mode A and mode B, respectively [19]. We can verify the conditions for the simultaneous eigenstate as and . The eigenvalue zeros for and imply and . This suggests the existence of strong correlations on the complex amplitudes of the two modes. We can see that and in the limit |ζ | → 1. Hence, in this limit, the TMSS approaches the EPR state.
In what follows we assume that ζ is real and positive. One may define the fraction of TMSS as an analog of the maximally entangled fraction in finite dimension systems. Since the TMSS |ψζ〉 of (39) has as its largest Schmidt coefficient, using the result of Appendix A we have and obtain the separable condition: Any separable state must satisfy
()
For the TMSS of (39), we can see the following pair appearance phenomena. When one find that the local state of A is a coherent state , the local state of B turns out to be another coherent state |ζα*〉. Similar to (1), the following relation holds for any complex amplitude α:
()
In order to see the role of entanglement in such pair appearance we may define the fraction of the phase-conjugate coherent-state pairs as follows:
()
where we introduced the real parameter λ ≥ 0 and the probability density
()
In the limit λ → 0, we have λ/pλ(α) → 1/π, and (pλ(α)/λ) | α〉〈α | d2α corresponds to the POVM elements of the double homodyne measurement on mode A (It satisfies ∫  | α〉〈α | d2α/π = 1). For notation convention we define the normalized state
()
which satisfies . Then, we can write the fraction as
()
For the TMSS of (39) we have
()
This quantity takes the maximum value of
()
when
()
Note that, in the limit λ → 0, we have the unit probability fmax  = 1 and ζ′ → ζ.

In what follows we show that (i) the maximum value of f in (43) for physical states is actually given by fmax  of (48) and determine (ii) the maximum value of f for classically correlated states.

Let us show that (i) λfmax (λ, ζ) corresponds to the operator norm of , that is, . To proceed, we determine the covariance matrix of and diagonalize this matrix.

Proof. Let us define the covariance matrix of

()
where is the set of the canonical operators of mode A and mode B. From (45) the covariance matrix of the operator is given by
()
where 1 is the identity operator of 4-by-4 matrices.

In order to diagonalize this matrix we define another matrix U(r) corresponding to the two-mode squeezing operator that transforms the canonical operators as follows:

()
The covariance matrix is diagonalized as follows:
()
where
()
and the squeezing parameter r is determined by
()
which is equivalent to tanhr = ζ′. Therefore, the operator is diagonalized by the two-mode squeezer as the product of thermal states:
()
Thus, we have the maximum eigenvalue
()
corresponding to the eigenstate U(r) | 0,0〉 = |ψζ′〉. Equation (57) proves the first statement (i) .

Note that in the limit λ → 0, we have fmax  → 1 for any ζ > 0. This means that with nearly unit probability, the TMSS assigns the complex-conjugate pair of coherent states as the EPR state does (see Figure 4). Note also that the maximum eigenvalue can be associated with the physical limit of the amplification task in [20].

Now, our question is the limit of the pair appearance f in (43) for classical correlated states. We can prove the following statement: (ii) When the state has no entanglement the maximum value of the operator becomes
()

Proof. In order to show this, let us write the partial transposition of the operator in the diagonal form:

()
where V is the beam-splitter transformation act on the coherent states as and we used the fact that the thermal state is diagonalized on the number-state basis in the final expression. From the diagonal form the maximum eigenvalue (operator norm) of is given by . Since an expectation value of a partial transposed operator for a product state corresponds to a expectation value of the original operator for another product state [16], we have . Using this relation we have
()
The equality holds when ρ0 = |0,0〉〈0,0|. This proves (58).

Consequently, it has turned out that the pair appearance of the phase-conjugate coherent states can be a signature of entanglement, and we obtain the following statement: the state ρ is entangled if there exist λ > 0 and ζ > 0 such that [21] (see Figure 5).

Details are in the caption following the image
Figure 5
Open in figure viewerPowerPoint
The fraction of the state pairs fR(0, ζ, ρ) defined in (43) cannot exceed 1/(1 + ζ2) for separable states, and the observation of the fraction beyond this limit is a signature of entanglement. This diagram is a continuous-variable analog of Figure 2. A counterpart of the identical-state-pair fraction g may be defined by lim λ→0[Γ(Ξ)/λ)]. Its classical limit is essentially zero.

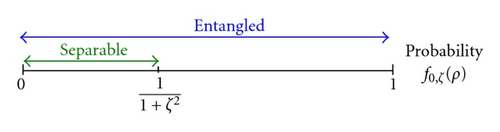
In Section 2.3, it is shown that the fraction of the identical-state pairs vanishes for the antisymmetric states and a smaller value of g can be a signature of entanglement on the two-qudit system. For the fraction of the identical-coherent-state pairs {|α〉|ζα〉} with the prior distribution pλ(α), it is clear that one can lower the expectation value less than any given positive number by choosing a product of number states with a sufficiently large photon number. Hence, the fraction of the identical-coherent-state pairs is not useful as a signature of entanglement in this regard.

3.2. Teleportation Fidelity and the Pair Appearance of Phase-Conjugate Coherent States

In this section we consider the process of continuous-variable quantum teleportation and investigate the equivalence between the teleportation fidelity and the fraction of the phase-conjugate coherent-state pairs.

Let us consider the process of continuous-variable quantum teleportation [22, 23] for a coherent state |α〉 from mode A′ to mode B by using a possibly entangled state ψ on the joint mode AB as in Figure 6. The teleportation process consists of the following two steps: (i) a Bell measurement of the joint mode AA′ and (ii) a feedforward displacement operation on mode B associated with the Bell-measurement outcome (x, p). The first step is accomplished by a half-beamsplitter transformation and two homodyne measurements. Suppose that the state of the joint mode AA′ is a product of coherent states |γ〉 A | α〉 A′. Then, the joint probability density that the Bell-measurement outcome is (x, p) can be written as
()
where the beam-splitter transformation is given by , and the complex amplitude is defined by . With this measurement outcome z and a gain parameter g′ ≥ 0, the second step can be described by the displacement operation on mode B. By using (61) and the P representation ψBA = ∫ d2βd2γP(β, γ) | β〉〈β|B⊗|γ〉〈γ|A, we can express the state after the teleportation process as
()
where we define
()
Note that ψBA′ is not a normalized density operator while 〈α* | ψBA′ | α*〉 A is a normalized density operator on mode B.
Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
A continuous-variable quantum teleportation process ℰ of an input coherent state |α〉 from mode A′ to mode B by using a possibly entangled state ψ on modes A and B. The outcome z of the Bell measurement on the joint mode AA′ is forwarded to make a displacement on mode B, where g′ ≥ 0 is the teleportation gain.
For the case of continuous-variable quantum channels [24] we may define the average gate fidelity as
()
The factor ζ is essential to describe the effect of loss or amplification [20, 21, 24]. Such an effect is inherent concept in the class of Gaussian operations [25].
If we set the gain parameter g′ = ζ we can write
()
with β = α + z*. From this expression we have
()
where we performed the integration of z with a change of the integration variable d2β = d2α. Hence, we have shown that the teleportation fidelity (64) is equivalent to the fraction of the phase-conjugate coherent-state pairs with λ = 0. Note that the final expression of (66) no more includes the parameter λ. This is because the displacement all over the phase space eliminates the information about the phase-space position of ψ (see (63)).

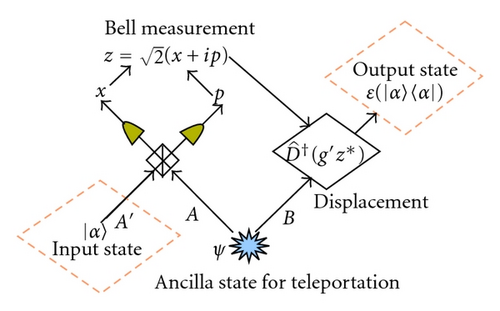
4. Summary

We have considered the probability that a bipartite quantum state contains the PCS pairs and/or identical-state pairs. We determine the physical limits and classical limits of these probability for the case of uniform distribution on qudit states. The classical limits give the separable conditions. We have also shown the equivalence between the average fidelity of quantum teleportation process and the probability of the PCS pairs on the resource state of the teleportation. A summary of the obtained statements in Sections 2.1–2.3 is given in Section 2.4.

For the case of uniform distribution on two mutually unbiased bases, a part of the problems becomes highly dependent on the dimension d. We have shown that the probability of the identical-state-pair appearance is useless for the entanglement verification when d is not a prime number. We have conjectured that the probability can be a signature of entanglement when d is a prime number. It is true when d = 2 and is numerically confirmed when d = 3.

We have also considered the probability that a two-mode continuous-variable state contains the phase-conjugate coherent-state pairs. We determine its physical limit and classical limit. We have also addressed its role in the process of continuous-variable quantum teleportation.

Acknowledgments

This work was supported by the Grant-in-Aid for the Global COE Program “The Next Generation of Physics, Spun from Universality and Emergence” from the Ministry of Education, Culture, Sports, Science and Technology (MEXT) of Japan. R. Namiki acknowledges support from JSPS.

    Appendices

    A. Maximum Separable Eigenvalue of Pure Entangled States

    In the main text, we have considered the maximum expectation value of certain observables under the constraint that the state is separable. This optimization problem is called the separable eigenvalue problem [26]. If the observable is an entangled pure state, the maximum value is the square of the largest Schmidt coefficient. Here we provide a formal proof.

    Proof. Any pure entangled state can be written in the Schmidt decomposed form as follows:

    ()
    with and . For any pure separable state |s〉 = ∑i ui | i〉∑j vj | j〉 with ∑j  | uj|2 = 1 and ∑j  | vj|2 = 1, we have ∑j  | ujvj|2 ≤ ∑i  | ui|2∑j  | vj|2 = 1 from Schwarz inequality and obtain
    ()
    The equality is achieved when uk = vk = δk,0. Since any separable state can be written as a convex combination of pure separable states, we can verify
    ()
    The convexity also implies that the optimization over the pure separable states is always sufficient for the separable eigenvalue problem.

    B. Another Expression of the Flip Operator

    Here, we give another diagonal expression of the flip operator defined in (24). In the main text we use the diagonal expression of (26).

    The matrix elements of with respect to the Bell basis of (13) is given by . From this relation we can diagonalize the flip operator:
    ()
    where
    ()

    C. Generation of the Fraction in a Symmetric Form

    In the expression of fR of (43), the systems A and B are not equivalently treated as the parameter ζ is only put on the states of B. Here, we will consider a symmetric formula and present a related separable condition. Let us define the operator, in which the position of ζ is moved from B to A on (45),
    ()
    Then, from the same procedure done on , we obtain the separable condition (see (60))
    ()
    We can verify the following relation for the convex combination of operators, with χ > 0:
    ()
    The bound can be achieved by ρ0 = |0,0〉〈0,0| again. Using this inequality we can obtain the following separable criterion. For any ξ > 0, and λ1, λ2, ζ1, ζ2 > 0, separable states must satisfy the following:
    ()

      The full text of this article hosted at iucr.org is unavailable due to technical difficulties.