We develop a generalized monotone method using coupled lower and upper solutions for Caputo fractional differential equations with periodic boundary conditions of order q, where 0 < q < 1. We develop results which provide natural monotone sequences or intertwined monotone sequences which converge uniformly and monotonically to coupled minimal and maximal periodic solutions. However, these monotone iterates are solutions of linear initial value problems which are easier to compute.

1. Introduction

The study of fractional differential equations has acquired popularity in the last few decades due to its multiple applications, see [1–5] for more information. However, it was not until recently that a study on the existence of solutions by using upper and lower solutions, which is well established for ordinary differential equations in [6], has been done for fractional differential equations. See [3, 7–16] for recent work.

In this paper we recall a comparison theorem from [3] for a Caputo fractional differential equation of order q, 0 < q < 1, with initial condition. We will use coupled lower and upper solutions combined with a generalized monotone method of initial value problems to prove the existence of coupled minimal and maximal periodic solutions. The results developed provide natural sequences and intertwined sequences which converge uniformly and monotonically to coupled minimal and maximal periodic solutions. Instead of the usual approach as in [6, 17] where the iterates are solutions of linear periodic boundary value problems we have used a generalized monotone method of initial value problems. This idea was presented in [18] for integrodifferential equations. The advantage of this method, compared to what was developed in [3, 15], is that it avoids computing the solution of the linear periodic boundary value problem using the Mittag-Leffler function at every step of the iterates. We also modify the comparison theorem which does not require the Hölder continuity condition as in [3].

2. Preliminary Definitions and Comparison Results

In this section we state some definitions and recall some results for a Caputo initial value problem which we need in our main results. Consider the initial value problem of the form:

()

Here,

is the Caputo derivative of order n − 1 < q ≤ n for t ∈ [a, b], which is defined in [1–3, 5] as

()

In this paper we will denote .

The relation between the Caputo fractional derivative and the Riemann-Liouville fractional derivative, D^q, is given by

()

Throughout this paper we consider the Caputo derivative of order q, for 0 < q < 1 and t ∈ [0,1]. We start by showing some comparison results relative to initial value problems with the Caputo fractional derivative of order q.

Lemma 2.1. Let m(t) ∈ C¹([0, T], ℝ). If there exists t₁ ∈ [0, T] such that m(t₁) = 0 and m(t) ≤ 0 on [0, T], then it follows that

()

Proof. Let t₁ ∈ [0, T], the using the relation (2.3) we have that

()

Since this lemma was proven in [8] for the Riemann Liouville derivative, we have that D^qm(t₁) ≥ 0 implies , and the proof is complete.

Remark 2.2. In [3] they proved the above result by assuming that m(t) is Hölder continuous of order λ > q. Although the proof is correct, it is not useful in the monotone method or any iterative method because we will not be able to prove that each of those iterates are Hölder continuous of order λ > q.

Now we are ready to establish the following comparison theorem.

Theorem 2.3. Let J = [0, T], f ∈ C[J × ℝ, ℝ], v, w ∈ C¹[J, ℝ], and for t ∈ J the following inequalities hold true,

()

Suppose further that f(t, u) satisfies the following Lipschitz condition,

()

then v(0) ≤ w(0) implies that

()

Proof. Assume first without loss of generality that one of the inequalities in (2.6) is strict, say , and v₀ < w₀, where v(0) = v₀ and w(0) = w₀. We will show that v(t) < w(t) for t ∈ J.

Suppose, to the contrary, that there exists t₁ such that 0 < t₁ ≤ T for which

()

Setting m(t) = v(t) − w(t) it follows that m(t₁) = 0 and m(t) ≤ 0 for t < t₁. Then by hypothesis and Lemma 2.1 we have that ^cD^qm(t₁) ≥ 0. Thus

()

which is a contradiction to the assumption v(t₁) = w(t₁). Therefore v(t) < w(t).

Now assume that the inequalities (2.6) are nonstrict. We will show that v(t) ≤ w(t).

Set w_ϵ(t) = w(t) + ϵλ(t), where ϵ > 0 and λ(t) = E_q[2Lt^q], where E_q is the one parameter Mittag-Leffler function. This implies that w_ϵ(0) = w₀ + ϵ > w₀ and w_ϵ(t) > w(t) for t ∈ (0, T].

Using (2.6) and the Lipschitz condition (2.7), we find that

()

Here we have utilized the fact that λ(t) is the solution of the initial value problem

()

Clearly there is no assumption on the growth of L > 0. Applying now the result for strict inequalities to v(t), w_ϵ(t), we get that v(t) < w_ϵ(t) for t ∈ J, for every ϵ > 0 and consequently making ϵ → 0, we get that v(t) ≤ w(t) for t ∈ J.

The following corollary will be useful in our main results.

Corollary 2.4. Let m ∈ C¹[J, ℝ] be such that

()

Then we have from the previous theorem the estimate

()

The result of the above corollary is still true even if L = 0, which we state separately and prove it.

Corollary 2.5. Let ^cD^qm(t) ≤ 0 on [0, T]. Then m(t) ≤ 0, if m(0) ≤ 0.

Proof. By definition of ^cD^qm(t) and by hypothesis,

()

which implies that m′(t) ≤ 0 on [0, T]. Therefore, m(t) ≤ m(0) ≤ 0 on [0, T].

Note that the above result may not be true for the Riemann Liouville derivative.

We recall a comparison result from [3] for periodic boundary conditions. As in Theorem 2.3, the proof does not require Hölder continuity.

Theorem 2.6. Let J = [0, T], f ∈ C[J × ℝ, ℝ], v, w ∈ C¹[J, ℝ], and for 0 < t ≤ T,

()

Suppose further that f(t, u) is strictly decreasing in u for each t, then

()

Proof. If the conclusion is not true; that is, if there exists t₀ ∈ [0, T] such that v(t₀) > w(t₀), then there exists an ε > 0 such that

()

Setting m(t) = v(t) − w(t) − ε we find that if t₀ ∈ (0, T], then

()

By Lemma 2.1 we have that ^cD^qm(t₀) ≥ 0. Thus, ^cD^qv(t₀) ≥ ^cD^qw(t₀). We now obtain by hypothesis and by the strictly decreasing nature of f(t, u) in u,

()

which is a contradiction.

If t₀ = 0, then

()

so v(T) > w(T), and by the above argument we also get a contradiction.

Hence v(t) ≤ w(t) for 0 ≤ t ≤ T and the proof is complete.

Two important cases of this theorem are the following which are useful to prove the uniqueness of the solution of a Caputo fractional differential equation with periodic boundary conditions.

Corollary 2.7. Let m ∈ C¹[J, ℝ] be such that

()

for 0 ≤ t ≤ T and M > 0. Then m(t) ≤ 0 for 0 ≤ t ≤ T.

Similarly, if

()

for 0 ≤ t ≤ T and M > 0. Then m(t) ≥ 0 for 0 ≤ t ≤ T.

Remark 2.8. It is to be noted that in the proof of these equivalent results from [3] we use Lemma 2.1 which does not require the Hölder continuity assumption.

A generelized monotone method for periodic boundary value problems was recently developed in [3, 15]. However it uses the approach established in [6] for ordinary differential equations where the iterates are solutions of the linear periodic boundary value problem,

()

where M > 0 and h ∈ C[J, ℝ].

The explicit solution of this equation is given by

()

where E_q and E_q,q are Mittag-Leffler functions with one and two parameters, respectively.

This poses a problem to compute the linear iterates since it involves Mittag-Leffler functions. The advantage of our method is that it does not require the Mittag-Leffler function in our computations.

Pandit et al. used the initial value problem to obtain a generalized monotone method in [18] for nonlinear integrodifferential equations with periodic boundary conditions. In the next section we develop a monotone method using this idea.

3. Generalized Monotone Method for the Nonlinear Periodic Boundary Value Problem via Initial Value Problem

In this section, we will develop a generalized monotone method for the nonlinear periodic boundary value problem (3.2), given below, by using coupled upper and lower solutions and the corresponding initial value problem (2.1), where f does not depend on u,

()

For that purpose consider the nonlinear periodic boundary value problem of the form:

()

where f, g ∈ C[J × ℝ, ℝ] and u ∈ C¹[J × ℝ].

If u ∈ C¹[0, T] satisfies the fractional differential equation

()

and u is such that u(0) = u(T) for t ∈ J, then u is a periodic solution of (3.2).

Furthermore, throughout this paper, we will assume that f is increasing in u and g is decreasing in u for t ∈ J.

Here below we provide the definition of coupled lower and upper solutions of (3.2).

Definition 3.1. Let v₀, w₀ ∈ C¹[J, ℝ]. Then v₀ and w₀ are said to be,

(i)
natural lower and upper solutions of (3.2) if
()
(ii)
coupled lower and upper solutions of Type I of (3.2) if
()
(iii)
coupled lower and upper solutions of Type II of (3.2) if
()
(iv)
coupled lower and upper solutions of Type III of (3.2) if,
()

We will state the following four theorems related to coupled lower and upper solutions of Type I and Type II, respectively. We develop the generalized monotone method for the periodic boundary value problem via the initial value problem approach. We obtain natural sequences and intertwined sequences which converge uniformly and monotonically to coupled minimal and maximal periodic solutions of (3.2).

In the next theorem, we use coupled lower and upper solutions of Type I and obtain natural sequences which converge uniformly and monotonically to coupled minimal and maximal periodic solutions of (3.2).

Theorem 3.2. Assume that

(A1)
v₀, w₀ are coupled lower and upper solutions of Type I for (3.2) with v₀(t) ≤ u(t) ≤ w₀(t) on J;
(A2)
f, g ∈ C[J × ℝ, ℝ], f(t, u(t)) is increasing in u and g(t, u(t)) is decreasing in u.

Then the sequences defined by

()

are such that v_n(t) → ρ(t) and w_n(t) → r(t) in C¹[J, ℝ] uniformly and monotonically, such that ρ and r are coupled minimal and maximal solutions of (3.2), respectively, provided that v₀ ≤ u ≤ w₀, where u is any periodic solution of (3.2). That is, ρ and r satisfy the coupled system

()

such that ρ ≤ u ≤ r.

Proof. By hypothesis, v₀ ≤ u ≤ w₀. We will show that v₀ ≤ v₁ ≤ u ≤ w₁ ≤ w₀.

It follows from (3.5) that

()

and by (3.8), we get that

()

Therefore, v₀(0) ≤ v₀(T) = v₁(0). If we let p = v₀ − v₁, then p(0) ≤ 0 and,

()

Since ^cD^qp ≤ 0 and p(0) ≤ 0, by Corollary 2.5 we have that p(t) ≤ 0 and, consequently, v₀(t) ≤ v₁(t) on J. By a similar argument we can show that v₁(t) ≤ u, u ≤ w₁(t), and w₁(t) ≤ w₀(t). Thus, v₀ ≤ v₁ ≤ u ≤ w₁ ≤ w₀.

Now we will show that v_k ≤ v_k+1 for k ≥ 1.

Assume that

()

for k > 1.

Let p = v_k − v_k+1. Then

()

so p(0) ≤ 0. By the increasing nature of f and the decreasing nature of g it follows that

()

Similarly, by Corollary 2.5 we have that p(t) ≤ 0 and consequently v_k(t) ≤ v_k+1(t).

By a similar argument we can show that w_k+1 ≤ w_k. Using the hypothesis that v₀(t) ≤ u(t) ≤ w₀(t) on J, the above argument and induction we can show that v_k+1 ≤ u ≤ w_k+1. Therefore for n > 1,

()

Now we have to show that the sequences converge uniformly. We will use Arzela-Ascoli theorem by showing that the sequences are uniformly bounded and equicontinuous.

First we show uniform boundedness. By hypothesis both v₀(t) and w₀(t) are bounded on [0, T], then there exists M > 0 such that for any t ∈ [0, T], |v₀(t)| ≤ M, and |w₀(t)| ≤ M. Since v₀(t) ≤ v_n(t) ≤ w₀(t) for each n > 0, it follows that

()

and consequently {v_n(t)} is uniformly bounded. By a similar argument {w_n(t)} is also uniformly bounded.

To prove that {v_n(t)} is equicontinuous, let 0 ≤ t₁ ≤ t₂ ≤ T. Then for n > 0,

()

Since {v_n(t)} and {w_n(t)} are uniformly bounded and f(t, u(t)) and g(t, u(t)) are continuous on [0, T], there exists independent of n such that

()

Thus, for any ε > 0 there exists δ > 0 independent of n such that for each n,

()

provided that |t₁ − t₂ | < δ.

Similarly we can prove that {w_n(t)} is equicontinuous and uniformly bounded.

This proves that {v_n(t)} and {w_n(t)} are uniformly bounded and equicontinuous on [0, T]. Hence by Arzela-Ascoli’s theorem there exist subsequences and which converge uniformly to ρ(t) and r(t), respectively. Since the sequences are monotone, the entire sequences converge uniformly.

We have shown that the sequences converge in C[0, T]. In order to show that they converge in C¹[0, T], observe that since each v_n is constructed as follows

()

we get that

()

Taking limits when n → ∞, we obtain by the Lebesgue dominated convergence theorem that

()

Hence v_n(t) → ρ(t) in C¹[0, T]. Furthermore, the above expression is equivalent to

()

By a similar argument w_n(t) → r(t) in C¹[0, T] and it can be shown that

()

Since v_n ≤ u ≤ w_n on [0, T] for all n, we get that ρ ≤ u ≤ r on [0, T] which shows that ρ and r are minimal and maximal periodic solutions of (3.2), respectively. This completes the proof.

Remark 3.3. In [3] the uniqueness is shown by making additional assumptions to Theorem 3.2 and using Corollary 2.7. However the iterates are solutions of the form (2.25). In our result, we have proved the existence of coupled minimal and maximal periodic solutions of (3.2), in particular if g ≡ 0 we get minimal and maximal periodic solutions of (3.2).

The next result also uses coupled upper and lower solutions of Type I. However, we obtain intertwined sequences which converge to coupled minimal and maximal periodic solutions of (3.2). The proof is similar to Theorem 3.2, hence we do not provide the proof.

Theorem 3.4. Assume that conditions (A1) and (A2) of Theorem 3.2 are true. Then the iterative scheme given by

()

give alternating monotone sequences {v_2n, w_2n+1} and {v_2n+1, w_2n} satisfying

()

for each n ≥ 1 on J, provided that v₀ ≤ u ≤ w₀.

Furthermore {v_2n, w_2n+1} → ρ and {v_2n+1, w_2n} → r in C¹[J, ℝ], where ρ and r are coupled minimal and maximal periodic solutions of (3.2), respectively; that is, if v₀ ≤ u ≤ w₀ then ρ ≤ u ≤ r, and ρ and r satisfy the coupled system

()

In the previous two theorems we assumed the existence of coupled lower and upper solutions of type I. We can state two more results involving coupled lower and upper solutions of Type II, however they require an additional assumption in order to obtain natural or intertwined sequences converging to coupled minimal and maximal periodic solutions of problem (3.2).

Theorem 3.5. Assume that

(B1)
v₀ and w₀ are coupled lower and upper solutions of Type II for (3.2) with v₀(t) ≤ w₀(t) on J,
(B2)
f, g ∈ C[J × ℝ, ℝ], f(t, u(t)) is increasing in u, and g(t, u(t)) is decreasing in u.

If u(t) is a solution of (3.2) such that v₀(t) ≤ u(t) ≤ w₀(t). Then the sequences defined by (3.27) give alternating monotone sequences {v_2n, w_2n+1} and {v_2n+1, w_2n} satisfying

()

for each n ≥ 1 on J, provided that v₀ ≤ w₁ ≤ u ≤ v₁ ≤ w₀.

Furthermore {v_2n, w_2n+1} → ρ and {v_2n+1, w_2n} → r in C¹[J, ℝ], where ρ and r are coupled minimal and maximal solutions of (3.2), respectively; that is, if v₀ ≤ u ≤ w₀ then ρ ≤ u ≤ r, and ρ and r satisfy the coupled system

()

Theorem 3.6. Assume that conditions (B1) and (B2) of Theorem 3.5 are true. Then the sequences defined by (3.8) and (3.9) are such that v_n(t) → ρ(t) and w_n(t) → r(t) in C¹[J, ℝ] uniformly and monotonically, provided that v₀ ≤ v₁ ≤ u ≤ w₁ ≤ w₀, where ρ and r are coupled minimal and maximal solutions of (3.2), respectively; that is, ρ ≤ u ≤ r and ρ and r satisfy the coupled system

()

Remark 3.7. The proof of Theorems 3.5 and 3.6 follow on the same lines as Theorem 3.2. However, it is easy to compute coupled lower and upper solutions of Type II.

4. Numerical Examples

In this section we present some numerical examples which are application of Theorem 3.5.

Example 4.1. Consider the problem

()

Clearly u ≡ 0 and u ≡ 1 are solutions of the equation.

Since H(u) = u − u² is increasing in u for u ≤ 0.5 and decreasing for u ≥ 0.5, we let

()

and v₀ = 1/2 and w₀ = 3/2 be lower and upper solutions of type II, respectively, because

()

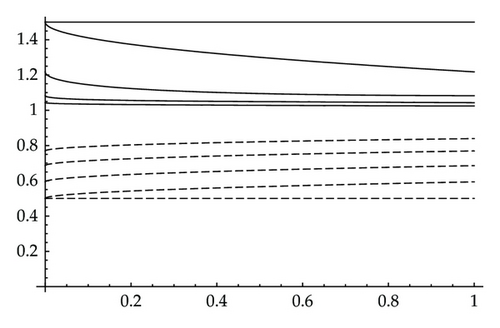
We construct our sequences according to Theorem 3.5 and show graphically in Figure 1 that {w_2n, v_2n+1} → 1.

Details are in the caption following the image — **Figure 1**
Open in figure viewer PowerPoint

Dashed: {v_2n, w_2n+1}. Solid: {w_2n, v_2n+1}.

Example 4.2. Consider the problem

()

Since H(t, u) = (u/8)−(u²/2)+(t/2) is increasing in u for u ≤ 0.125 and decreasing for u ≥ 0.125, we let

()

and v₀ = 1/8 and w₀ = 1 be lower and upper solutions of type II, respectively, because

()

where 0 ≤ t ≤ 1/2.

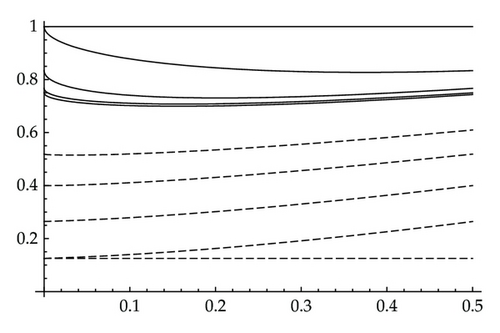
Using Theorem 3.5 we show in Figure 2 four steps of {v_2n, w_2n+1} and four steps of {w_2n, v_2n+1}. Observe that {w_2n, v_2n+1} converges more quickly to the periodic solution.

Example 4.3. Consider

()

Since f(t, u) = −(u²/2) + t(1 − t) is increasing in u for u ≤ 0 and decreasing for u ≥ 0,

()

and v₀ = 0 and w₀ = 1 are lower and upper solutions of type II, respectively, because

()

where 0 ≤ t ≤ 1/2, which implies that 0 ≤ t(1 − t) ≤ 0.25

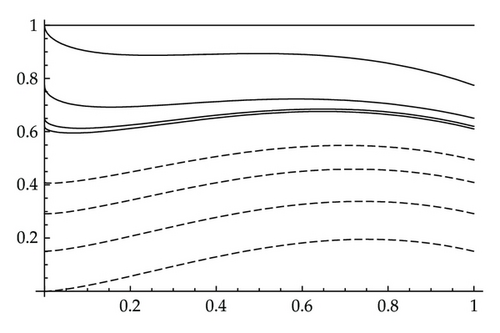
Once again using Theorem 3.5 we computed in Figure 3 four steps of {v_2n, w_2n+1} and 4 steps of {w_2n, v_2n+1}. As in the previous examples {w_2n, v_2n+1} converges more quickly to the periodic solution.

5. Concluding Remarks

In our main results as well as in our numerical results we have not used the assumption needed to obtain unique solution of (3.2). If we make appropriate uniqueness assumption on the nonlinear terms f(t, u) and g(t, u) then our linear iterates will require the computation of the Mittag-Leffler function. We plan to take up this work in the near future.

References

1 Diethelm K., The Analysis of Fractional Differential Equations, 2004, Springer, Braunschweig, Germany, https://doi.org/10.1007/978-3-642-14574-2, 2680847.
Google Scholar
2 Kilbas A. A., Srivastava H. M., and Trujillo J. J., Theory and Applications of Fractional Differential Equations, 2006, 204, Elsevier, Amsterdam, The Netherlands, North-Holland Mathematics Studies, 2218073.
10.1016/S0304-0208(06)80001-0
Google Scholar
3 Lakshmikantham V., Leela S., and Vasundhara D. J., Theory of Fractional Dynamic Systems, 2009, Cambridge Scientific Publishers.
Google Scholar
4 Oldham K. B. and Spanier J., The Fractional Calculus, 1974, Academic Press, New York, NY, USA, 0361633.
Google Scholar
5 Podlubny I., Fractional Differential Equations, 1999, 198, Academic Press, San Diego, Calif, USA, Mathematics in Science and Engineering, 1658022.
Web of Science® Google Scholar
6 Ladde G. S., Lakshmikantham V., and Vatsala A. S., Monotone Iterative Techniques for Nonlinear Differential Equations, 1985, Pitman, Boston, Mass, USA, 855240.
Google Scholar
7 Denton Z. and Vatsala A. S., Fractional integral inequalities and applications, Computers & Mathematics with Applications. (2010) 59, no. 3, 1087–1094, https://doi.org/10.1016/j.camwa.2009.05.012, 2579473, ZBL1189.26044.
10.1016/j.camwa.2009.05.012
Web of Science® Google Scholar
8 Denton Z. and Vatsala A. S., Monotone iterative technique for finite systems of nonlinear Riemann-Liouville fractional differential equations, Opuscula Mathematica. (2011) 31, no. 3, 327–339, 2802898, ZBL1232.34012.
10.7494/OpMath.2011.31.3.327
Google Scholar
9 Lakshmikantham V. and Vatsala A. S., Theory of fractional differential inequalities and applications, Communications in Applied Analysis. (2007) 11, no. 3-4, 395–402, 2368191, ZBL1159.34006.
Google Scholar
10 Lakshmikantham V. and Vatsala A. S., Basic theory of fractional differential equations, Nonlinear Analysis: Theory, Methods & Applications. (2008) 69, no. 8, 2677–2682, https://doi.org/10.1016/j.na.2007.08.042, 2446361, ZBL1161.34001.
10.1016/j.na.2007.08.042
Web of Science® Google Scholar
11 Lakshmikantham V. and Vatsala A. S., General uniqueness and monotone iterative technique for fractional differential equations, Applied Mathematics Letters. (2008) 21, no. 8, 828–834, https://doi.org/10.1016/j.aml.2007.09.006, 2436173, ZBL1161.34031.
10.1016/j.aml.2007.09.006
Web of Science® Google Scholar
12 McRae F. A., Monotone iterative technique and existence results for fractional differential equations, Nonlinear Analysis: Theory, Methods & Applications. (2009) 71, no. 12, 6093–6096, https://doi.org/10.1016/j.na.2009.05.074, 2566513.
10.1016/j.na.2009.05.074
Web of Science® Google Scholar
13 McRae F. A., Monotone method for periodic boundary value problems of Caputo fractional differential equations, Communications in Applied Analysis. (2010) 14, no. 1, 73–79, 2662001, ZBL1208.34009.
Google Scholar
14 Ramírez J. D. and Vatsala A. S., Monotone iterative technique for fractional differential equations with periodic boundary conditions, Opuscula Mathematica. (2009) 29, no. 3, 289–304, 2551901, ZBL1197.26007.
10.7494/OpMath.2009.29.3.289
Google Scholar
15 Ramírez J. D. and Vatsala A. S., Generalized monotone method for Caputo fractional differential equation with periodic boundary condition, 4, Proceedings of Neural, Parallel, and Scientific Computations, 2010, Atlanta, Ga, USA, Dynamic, 332–337, 2762500.
Google Scholar
16 Ramírez J. D. and Vatsala A. S., Monotone method for nonlinear Caputo fractional boundary value problems, Dynamic Systems and Applications. (2011) 20, no. 1, 73–88, 2829459, ZBL1234.26019.
Web of Science® Google Scholar
17 West I. H. and Vatsala A. S., Generalized monotone iterative method for integro differential equations with periodic boundary conditions, Mathematical Inequalities & Applications. (2007) 10, no. 1, 151–163, https://doi.org/10.7153/mia-10-13, 2286701, ZBL1114.65159.
10.7153/mia-10-13
Web of Science® Google Scholar
18 Pandit S. G., Dezern D. H., and Adeyeye J. O., Periodic boundary value problems for nonlinear integro-differential equations, 4, Proceedings of Neural, Parallel, and Scientific Computations, 2010, Atlanta, Ga, USA, Dynamic, 316–320, 2762503.
Google Scholar

Citing Literature

All articles

Generalized Monotone Iterative Technique for Caputo Fractional Differential Equation with Periodic Boundary Condition via Initial Value Problem

Abstract

1. Introduction

2. Preliminary Definitions and Comparison Results

3. Generalized Monotone Method for the Nonlinear Periodic Boundary Value Problem via Initial Value Problem

4. Numerical Examples

5. Concluding Remarks

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Generalized Monotone Iterative Technique for Caputo Fractional Differential Equation with Periodic Boundary Condition via Initial Value Problem

Abstract

1. Introduction

2. Preliminary Definitions and Comparison Results

3. Generalized Monotone Method for the Nonlinear Periodic Boundary Value Problem via Initial Value Problem

4. Numerical Examples

5. Concluding Remarks

References

Citing Literature

Figures

References

Related

Information