Volume 2012, Issue 1 749847

Research Article

Open Access

A Matrix Method for Determining Eigenvalues and Stability of Singular Neutral Delay-Differential Systems

Jian Ma,

Jian Ma

Department of Mathematics, Harbin Institute of Technology, Harbin 150001, China hit.edu.cn

Department of Mathematics, Northeast Forestry University, Harbin 150040, China nefu.edu.cn

Search for more papers by this author

Baodong Zheng,

Corresponding Author

Baodong Zheng

[email protected]

Department of Mathematics, Harbin Institute of Technology, Harbin 150001, China hit.edu.cn

Search for more papers by this author

Chunrui Zhang,

Chunrui Zhang

Department of Mathematics, Northeast Forestry University, Harbin 150040, China nefu.edu.cn

Search for more papers by this author

Jian Ma,

Jian Ma

Department of Mathematics, Harbin Institute of Technology, Harbin 150001, China hit.edu.cn

Department of Mathematics, Northeast Forestry University, Harbin 150040, China nefu.edu.cn

Search for more papers by this author

Baodong Zheng,

Corresponding Author

Baodong Zheng

[email protected]

Department of Mathematics, Harbin Institute of Technology, Harbin 150001, China hit.edu.cn

Search for more papers by this author

Chunrui Zhang,

Chunrui Zhang

Department of Mathematics, Northeast Forestry University, Harbin 150040, China nefu.edu.cn

Search for more papers by this author

First published: 04 June 2012

https://doi.org/10.1155/2012/749847

Citations: 6

Academic Editor: Zhiwei Gao

Share a link

Email
Wechat
Bluesky

Abstract

The eigenvalues and the stability of a singular neutral differential system with single delay are considered. Firstly, by applying the matrix pencil and the linear operator methods, new algebraic criteria for the imaginary axis eigenvalue are derived. Second, practical checkable criteria for the asymptotic stability are introduced.

1. Introduction

Nowadays, the time-delay systems have became an important natural models in physics, engineering, multibody mechanics, computer-aided design, and economic systems. The theory on ordinary differential equations with delays have been discussed for decades in a wide range, so there are very many results for them. Especially, the eigenvalues and the stability analysis of time-delay systems have received much attention of researchers and many excellent results have been obtained, see [1–6]. Certainly most of them had been focused on the analytical methods or numerical methods, such as V-functional methods, Laplace transformation, Runge-Kutta methods, and linear multistep methods. In [7–9], the numerical techniques for the computation of the eigenvalues were discussed. In [10], Zhu and Petzold researched the asymptotic stability of delay-differential-algebraic equations by applying the θ-methods, Runge-Kutta methods, and linear multistep methods. These methods play the key roles at last. But in recent years, algebraic methods are developing fast, especially for the research on the more complex systems, such as the n-dimensional systems. Though the algebraic methods as a new and effective tool is also applied to analyze the time-delay systems [2, 3], the results are very few.

In this paper, we will discuss the differential-algebraic equations by the algebraic methods. Their dynamics have not been well understood yet.

Example 1.1. Consider the simple differential-algebraic system:

()

where t ≥ 0, τ ≥ 0, and x₁ and x₂ are given by continuous functions on the initial interval (−τ, 0]. So we have the solution:

()

where c is a constant. From the solution, we find that the solution depends on future integrals of the input f(t). This interesting phenomenon arrested many scholars to research. For a general n-dimensional differential equations with delay, we can note by

()

where B, A₀, A₁ ∈ R^n×n, Rank B ≤ n, t ≥ 0, τ ≥ 0, and X(t) ∈ Rⁿ is given by continuous functions on the initial interval (−τ, 0]. When Rank B = n, we called it the retarded differential equations. It can be improved as

()

Many scholars have widely researched the delay-independent or delay-dependent stability and asymptotic stability by analytic methods or numerical methods. When Rank B < n, it is called a singular (or degenerated) delay-differential equations. The imaginary axis eigenvalues are discussed by using matrix pencil, see [2]. But because of the complex nature of the singular differential systems with delay, the research is very difficult by using the analytical treatment. So few studies on the stability and the bifurcations have been conducted so far. Particulary, for the singular neutral differential systems with delays, there are hardly flexible and efficient verdicts.

In this paper, we will apply the algebraic methods to discuss the stability of a singular neutral differential system with a single delay, as follows:

()

where B₀, B₁, A₀, A₁ ∈ ℝ^n×n, x ∈ ℝⁿ, τ ≥ 0. For the system (1.5), if det B₀ ≠ 0, we can improve it as the form

()

It is a neutral differential equation with a single delay. The problem of computing imaginary axis eigenvalues on the system (1.6) has been previously studied in [11]. Here, we consider the state rank B₀ ≤ n. The solvability of the system (1.5), which is essentially the existence and the uniqueness of the solution, is determined by the regularity. The matrix pencil (B₀, A₀) is said to be regular if sB₀ + A₀ is not identically singular for any complex s. If (B₀, A₀) is regular, the zero s of det (sB₀ + A₀) is called the eigenvalue of the matrix pencil (B₀, A₀). From [12], we know that the system (1.5) is solvable if and only if (B₀, A₀) is regular. So, in this paper, we suppose that (B₀, A₀) is regular. In the following, we will analyze the eigenvalues and the stability of the system (1.5).

2. The Algebraic Criteria for Determining Imaginary Axis Eigenvalues

Firstly, we research an ordinary differential equation, which will motivate our analysis. Consider

()

where B₀, B₁, A₀, A₁ ∈ ℝ^n×n, X, Y ∈ ℂ^n×n. Let V denote the vector space V = ℂ^n×n × ℂ^n×n and E, F denote the operators on V, given by

()

With

, the system (2.1) can be written as

()

Supposing

is a matrix solution of the system (2.1), we have

()

For any complex s, let T = T(s) be the operator T = sE − F; then

()

For any complex s, let T⁺ = T⁺(s) : V → V, satisfying

()

For any complex s, let Λ = Λ(s), satisfying

()

By simple computations, we can get

()

Expressing by the operator language, that is,

()

In the following, we will convert matrix ordinary differential equation (2.3) to vector form. Let ξ be the elementary transform,

, that is,

()

Let

, and

()

Using the property of the Kronecker product, we have

()

where A, B, X ∈ ℂ^n×n. So (2.3) can be written as

()

Similarly, by denoting

as follows

()

we have

()

Lemma 2.1. For all complex s, , and so det T₀(s) = ±det Λ₀(s).

Proof. Let , where a = (sB₀ − A₀) ⊗ I, b = (sB₁ − A₁) ⊗ I, c = I ⊗ (sB₁ + A₁), and d = I ⊗ (sB₀ + A₀). Noting the Kronecker product identities (I ⊗ M)(N ⊗ I) = (N ⊗ I)(I ⊗ M) = N ⊗ M, we have db = bd, bc = cb. By regularity of (B₀, A₀), we know sB₀ + A₀ is nonsingular for enough complex s. So by the property of the polynomial and easy computations, we can get that for any complex s. Elsewhere,

()

Thus

()

Theorem 2.2. Any imaginary axis eigenvalue of the systems (1.5) is a zero point of det Λ₀(s) and thus also one of the eigenvalues of the matrix pencil (E₀, F₀).

Proof. The matrix polynomial for the system (1.5) is

()

Let s = iw be an imaginary axis eigenvalue of the system (1.5) and v is associated eigenvector, ∥v∥ = 1. We have p(s, e^−sτ)v = 0. By conjugating and transforming, we can get

()

Via the elementary transform ξ, we get

()

that is, Λ₀(s)u = 0, u = ξ(vv^*). We know that det Λ₀(s) = 0, and so

()

From Theorem 2.2, we know that all of the imaginary axis eigenvalues of the system (1.5) are zero points of the algebraic equation

()

Corollary 2.3. If det (B₀ ⊗ B₀ − B₁ ⊗ B₁) ≠ 0, then E₀ is invertible, and any imaginary axis eigenvalue of the systems (1.5) is the eigenvalue of .

Proof. By proof of Lemma 2.1, we have

()

The corollary follows immediately from Theorem 2.2.

Corollary 2.4. Any imaginary axis eigenvalue of the system with single delay

()

is an eigenvalue of

Proof. It follows immediately from Theorem 2.2.

In fact, the above result contains the system (1.6). For the system (1.6), we also have the following corollary.

Corollary 2.5 (see Jarlebring and Hochstenbach [2], Theorem 1.)For the system (1.6), the imaginary axis eigenvalues are the roots of the equation

()

Remark 2.6. In fact, (2.23) or (2.26) is usually called a polynomial eigenvalue problem. The classical and most widely used approach to research the polynomial eigenvalue problems is linearization, where the polynomial is converted into a larger matrix pencil with the same eigenvalues. There are many forms for the linearization: the companion form is most typically commission. The linearization method is also an important tool to research the characteristic equations in algebraic methods, see [2, 13].

From the above results, we find that the imaginary axis eigenvalues of the system (1.5) or (1.6) can be computed via the algebraic equation (2.23) and (2.26). The imaginary eigenvalues play an important role in the stability. Next, we will use the results to discuss the stability of the systems. At first, we will give the condition of the delay-independent stability on the system (1.5). Secondly, we will address the problem of finding the critical delays of the system (1.6), that is, the delay such that the system (1.6) has purely imaginary eigenvalues.

3. The Algebraic Criteria of the Asymptotic Stability

The stability of the delay ordinary differential equations has been widely discussed [14, 15]. It is well known that the Lyapunov-Krasovskii functional approach is the important analytic method to find the delay-independent stability criteria, which do not include any information on the size of delay. The main ideas for developing algebraic criteria of the stability analysis on the systems can be found in many works, such as “The Degenerate Differential Systems with Delay” (W. Jiang, 1998, [12]). The results for singular neutral differential equations are still very few, especially by algebraic methods.

Next we first research the delay-independent stability of the system (1.5). The characteristic equation for the system(1.5) is denoted again by

()

From [12], we known that the solution of the neutral time-delay systems is asymptotically stable if all roots of (3.1) have negative real part bounded away from 0, that is, there exists a number δ > 0, such that Re(s) ≤ −δ < 0 for any root s of (3.1). Especially for the system (1.5), Zhu and Petzold had found that there must exist the δ, if the condition |u^TB₀u| ≥ |u^TB₁u| for all u ∈ ℝⁿ holds, see [10]. So from [3, 10], we can get the following theorem.

Theorem 3.1. Let s be the zeros of (2.23). If the coefficient matrices of the system (1.5) satisfies the following conditions:

(i)
Reλ < 0, λ ∈ σ(B₀, −A₀),
(ii)
max _Res=0ρ((sB₀ − A₀) ⁻¹(sB₁ − A₁)) < 1,

then the system (1.5) is asymptotically stable for all τ ≥ 0, that is, the stability of the systems (1.5) is delay independent.

Proof. It follows immediately from [10].

In the following, we consider the neutral system (1.6), whose characteristic equation is denoted by

()

It is well known that the spectrum of the neutral delay systems exhibits some discontinuity properties, that is to say, an infinitesimal change of the delay parameter may cause the stability of the system to shift. These discontinuity properties are closely related to the essential spectrum of the system. The critical condition for a stability switch of a neutral delay system is that the rightmost eigenvalue goes from the left complex half-plane into the right complex half-plane by passing the imaginary axis. So the appearance of the imaginary axis eigenvalue is the critical condition. In Section 2, we find all of the imaginary axis eigenvalues. Let the delay be a parameter. In the following, we will find the critical value of the delay parameter such that the stability switch occurs. It is known that, if a neutral delay system is stable, it is necessary that its neutral part must be stable. For the system (1.6), this requirement concerns the stability of the difference equation:

()

The eigenvalues of (3.3) are called the essential spectrum of the system (1.6). We know that (3.3) is stable if ρ(B₁) < 1. It is important to point out that, under this assumption, the condition Re(s) ≤ −δ < 0 can be improved to Re(s) < 0. Our task is to find the critical delay where the system (1.6) becomes unstable. So we have the following theorem.

Theorem 3.2. Supposing all of the eigenvalues of matrix A₀ have negative real part and ρ(B₁) < 1, one has the following.

(i)
If for any root s of (3.2), Re(s) < 0, else if for any root s = iw, w > 0, z = e^−sτ, |z| < 1, then system (1.6) is asymptotic stability for any τ ≥ 0, that is, stability is delay independent.
(ii)
Otherwise, for each root s = iw, w > 0, |z| = 1, one can get the minimal critical value of delay parameter τ^*, such that if τ ∈ [0, τ^*), then system (1.6) is asymptotic stability, and when τ ≥ τ^*, the stability of system (1.6) changes, that is, the system (1.6) is delay-dependent stable and generates bifurcation in τ = τ^*.

Example 3.3. Consider a neutral neural networks with a single delay, see [16]:

()

Now we rewrite system (3.4) as the matrix equations:

()

The linearization of the system (3.4) around the origin is given by

()

where

()

Assume that a = −2, b = −1.5, a₂ = 0.3, b₂ = −0.3, and f(x) = g(x) = tanh(x). We carry out the numerical simulations for system (3.4). From (2.26), by MATLAB computation, we can get the imaginary eigenvalue s≐±0.445i, τ^*≐0.45. From Theorem (3.2), we know that the zero solution of the system (3.4) is delay-dependent stable. The direction of the Hopf bifurcation at τ = τ^* is supercritical and the bifurcating periodic solutions are asymptotically stable. The simulation results are shown in Figures 1 and 2.

Details are in the caption following the image — **Figure 1 (a)**
Open in figure viewer PowerPoint

For system (3.4), when τ = 0.44 < τ^*, the equilibrium is asymptotically stable.

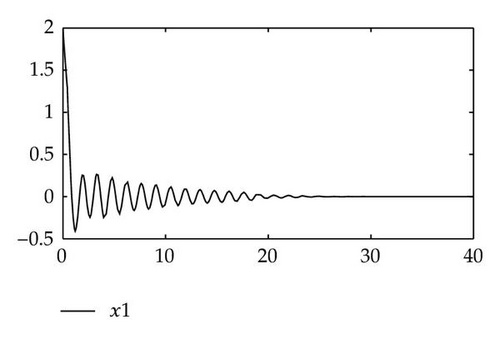
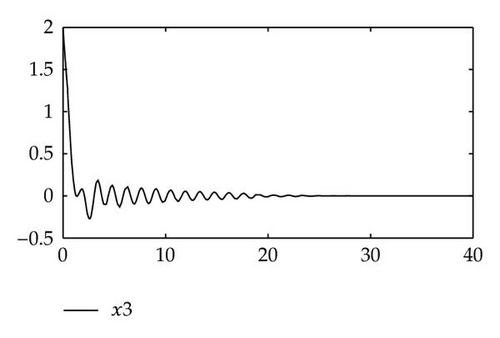
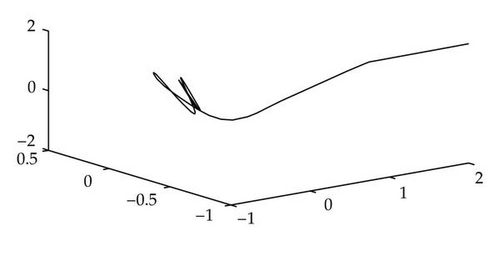
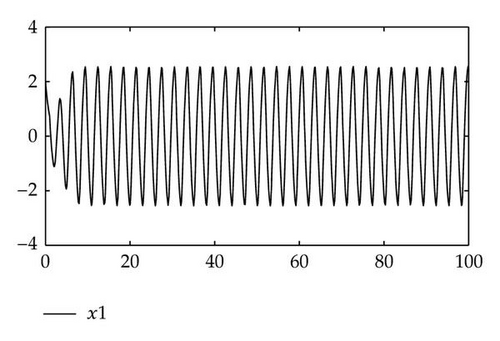
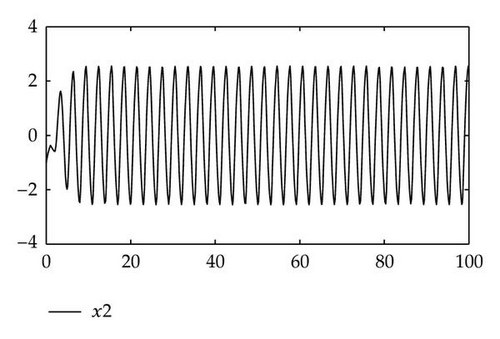
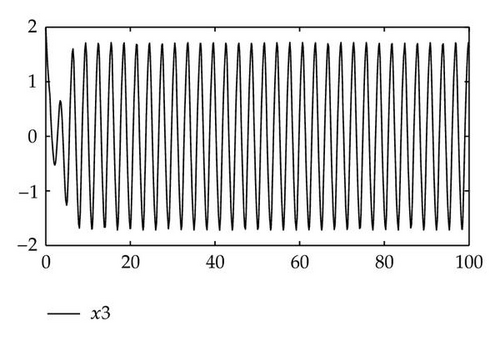
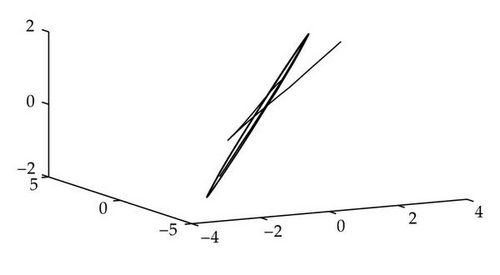
4. Conclusion

In this paper, we consider a singular neutral differential system with a single delay. Via applying the algebraic method, that is, the matrix pencil and the linear operators, we discussed the eigenvalues and the stability of the time-delay systems (1.5) and (1.6). By using MATLAB, we could easily compute imaginary eigenvalues from the algebraic equation (2.23) or (2.26). In fact, we only find the imaginary axis eigenvalues, which are the small part of the infinite eigenvalues. So compared with the analytic methods and the numerical methods, the algebraic methods are more simple and more explicit for some time-delay system. Certainly, applying the algebraic methods to analyze the dynamical properties of the singular neutral differential systems with delays is a new and immature field. So we believe that the algebraic methods used to research the stability of the dynamical systems would be more interesting in the future.

Acknowledgments

The National Natural Science Foundation of China (10871056) and the Fundamental Research Funds for the Central Universities (DL12BB24) are greatly acknowledged.

References

1 Hale J. K., Infante E. F., and Tsen F. S. P., Stability in linear delay equations, Journal of Mathematical Analysis and Applications. (1985) 105, no. 2, 533–555, https://doi.org/10.1016/0022%2D247X(85)90068%2DX, 778486.
10.1016/0022-247X(85)90068-X
Web of Science® Google Scholar
2 Jarlebring E. and Hochstenbach M. E., Polynomial two-parameter eigenvalue problems and matrix pencil methods for stability of delay-differential equations, Linear Algebra and its Applications. (2009) 431, no. 3-4, 369–380, 2528937, https://doi.org/10.1016/j.laa.2009.02.008, ZBL0569.34061.
10.1016/j.laa.2009.02.008
Web of Science® Google Scholar
3 Campbell S. L. and Linh V. H., Stability criteria for differential-algebraic equations with multiple delays and their numerical solutions, Applied Mathematics and Computation. (2009) 208, no. 2, 397–415, 2493832, https://doi.org/10.1016/j.amc.2008.12.008, ZBL1170.65063.
10.1016/j.amc.2008.12.008
Web of Science® Google Scholar
4 Gao Z., PD observer parametrization design for descriptor systems, Journal of the Franklin Institute. (2005) 342, no. 5, 551–564, https://doi.org/10.1016/j.jfranklin.2005.03.001, 2150731, ZBL1169.65079.
10.1016/j.jfranklin.2005.03.001
Web of Science® Google Scholar
5 Gao Z. and Ding S. X., Actuator fault robust estimation and fault-tolerant control for a class of nonlinear descriptor systems, Automatica. (2007) 43, no. 5, 912–920, https://doi.org/10.1016/j.automatica.2006.11.018, 2306739, ZBL1141.93317.
10.1016/j.automatica.2006.11.018
Web of Science® Google Scholar
6 Gao Z., Breikin T., and Wang H., Reliable observer-based control against sensor failures for systems with time delays in both state and input, IEEE Transactions on Systems, Man, and Cybernetics A. (2008) 38, no. 5, 1018–1029, https://doi.org/10.1109/TSMCA.2008.923050.
10.1109/TSMCA.2008.923050
Web of Science® Google Scholar
7 Simos T. E., Closed Newton-Cotes trigonometrically-fitted formulae of high order for long-time integration of orbital problems, Applied Mathematics Letters. (2009) 22, no. 10, 1616–1621, https://doi.org/10.1016/j.aml.2009.04.008, 2561745, ZBL1117.93019.
10.1016/j.aml.2009.04.008
Web of Science® Google Scholar
8 Stavroyiannis S. and Simos T. E., Optimization as a function of the phase-lag order of nonlinear explicit two-step P-stable method for linear periodic IVPs, Applied Numerical Mathematics. (2009) 59, no. 10, 2467–2474, https://doi.org/10.1016/j.apnum.2009.05.004, 2553148, ZBL1171.65449.
10.1016/j.apnum.2009.05.004
Web of Science® Google Scholar
9 Simos T. E., Exponentially and trigonometrically fitted methods for the solution of the Schrödinger equation, Acta Applicandae Mathematicae. (2010) 110, no. 3, 1331–1352, 2639174, https://doi.org/10.1007/s10440%2D009%2D9513%2D6.
10.1007/s10440-009-9513-6
Web of Science® Google Scholar
10 Zhu W. and Petzold L. R., Asymptotic stability of linear delay differential-algebraic equations and numerical methods, Applied Numerical Mathematics. (1997) 24, no. 2-3, 247–264, https://doi.org/10.1016/S0168%2D9274(97)00024%2DX, 1464727, ZBL1192.65111.
10.1016/S0168-9274(97)00024-X
Web of Science® Google Scholar
11 Louisell J., A matrix method for determining the imaginary axis eigenvalues of a delay system, Institute of Electrical and Electronics Engineers. (2001) 46, no. 12, 2008–2012, 1878231, https://doi.org/10.1109/9.975510, ZBL0879.65060.
10.1109/9.975510
Google Scholar
12 Jiang W., The Degenerate Differential Systems with Delay, 1998, Anhui University, Hefei, China.
Google Scholar
13 Mackey D. S., Mackey N., Mehl C., and Mehrmann V., Vector spaces of linearizations for matrix polynomials, SIAM Journal on Matrix Analysis and Applications. (2006) 28, no. 4, 971–1004, https://doi.org/10.1137/050628350, 2276550, ZBL1007.34078.
10.1137/050628350
Web of Science® Google Scholar
14 Michiels W. and Vyhlídal T., An eigenvalue based approach for the stabilization of linear time-delay systems of neutral type, Automatica. (2005) 41, no. 6, 991–998, https://doi.org/10.1016/j.automatica.2004.11.032, 2157698, ZBL1132.65027.
10.1016/j.automatica.2004.11.032
Web of Science® Google Scholar
15 Jarlebring E., On critical delays for linear neutral delay systems, Proceedings of the European Control Conference (ECC ′07), 2007, Kos, Greece.
Google Scholar
16 Li L. and Yuan Y., Dynamics in three cells with multiple time delays, Nonlinear Analysis. Real World Applications. (2008) 9, no. 3, 725–746, https://doi.org/10.1016/j.nonrwa.2006.12.015, 2392371, ZBL1091.93026.
10.1016/j.nonrwa.2006.12.015
Web of Science® Google Scholar

Citing Literature

All articles

A Matrix Method for Determining Eigenvalues and Stability of Singular Neutral Delay-Differential Systems

Abstract

1. Introduction

2. The Algebraic Criteria for Determining Imaginary Axis Eigenvalues

3. The Algebraic Criteria of the Asymptotic Stability

4. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

A Matrix Method for Determining Eigenvalues and Stability of Singular Neutral Delay-Differential Systems

Abstract

1. Introduction

2. The Algebraic Criteria for Determining Imaginary Axis Eigenvalues

3. The Algebraic Criteria of the Asymptotic Stability

4. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Related

Information