An integrable 2-component Camassa-Holm (2-CH) shallow water system is studied by using integral bifurcation method together with a translation-dilation transformation. Many traveling wave solutions of nonsingular type and singular type, such as solitary wave solutions, kink wave solutions, loop soliton solutions, compacton solutions, smooth periodic wave solutions, periodic kink wave solution, singular wave solution, and singular periodic wave solution are obtained. Further more, their dynamic behaviors are investigated. It is found that the waveforms of some traveling wave solutions vary with the changes of parameter, that is to say, the dynamic behavior of these waves partly depends on the relation of the amplitude of wave and the level of water.

1. Introduction

In this paper, employing the integral bifurcation method together with a translation-dilation transformation, we will study an integrable 2-component Camassa-Holm (2-CH) shallow water system [1] as follows:

()

which is a nonlinear dispersive wave equation that models the propagation of unidirectional irrotational shallow water waves over a flat bed [2], as well as water waves moving over an underlying shear flow [3]. Equation (1.1) also arises in the study of a certain non-Newtonian fluids [4] and also models finite length, small amplitude radial deformation waves in cylindrical hyperelastic rods [5], where m = u − (1/3)δ²u_xx + κ/2, σ = ±1 and

are two dimensionless parameters. The interpretation of (u, ρ), respectively, describes the horizontal fluid velocity and the density in the shallow water regime, where the variable u(x, t) describes the horizontal velocity of the fluid in x direction at time t, and the variable ρ(x, t) is related to the free surface elevation from equilibrium position (or scalar density) with the boundary assumptions. The parameter ℏ denotes the level of water, the parameter

denotes the typical amplitude of the water wave, and the parameter λ denotes the typical wavelength of the water wave. The constant κ denotes the speed of the water current which is related to the shallow water wave speed. The case σ = ±1, respectively, corresponds to the two situations in which the gravity acceleration points downwards and upwards. Especially, when the speed of the water current κ = 0 and the parameter σ = 1, (1.1) becomes the following form

()

where

. The system (1.2) appeared in [1], which was first derived by Constantin and Ivanov from the Green-Naghdi equations [6, 7] via the hydrodynamical point of view. Under the scaling

, (1.1) can be reduced to the following two-component generalization of the well-known 2-component Camassa-Holm (2-CH) system [1, 8–10]:

()

where m = u − (1/3)δ²u_xx + κ/2. The equation (1.3) attracts much interest since it appears. Attention was more paid on the local well-posedness, blow-up phenomenon, global existence, and so forth. When κ = 0, (1.3) has been studied by many authors, see [11–26] and references cited therein. Especially, under the parametric conditions δ = 1, ρ = 0, σ = −1, (1.3) can be reduced to the celebrated Camassa-Holm equation [27, 28],

()

In 2006, the integrability of (1.3) for σ = −1 was proved and some peakon and multikink solutions of this system were presented by Chen et al. in [9]. In 2008, the Lax pair of (1.3) for any value of σ was given by Constantin and Ivanov in [1]. In [29], by using the method of dynamical systems, under the traveling wave transformation u(x, t) = ϕ(x − ct), ρ(x, t) = ψ(x − ct), some explicit parametric representations of exact traveling wave solutions of (1.3) were obtained. But the loop solitons were not obtained in [29]. In [30], under σ = −1, one-loop and two-loop soliton solutions and multisoliton solutions of (1.3) are obtained by using the Darboux transformations.

Although (1.1) can be reduced to (1.3) by the scaling transformation , the dynamic properties of some traveling wave solutions for these two equations are very different. In fact, the dynamic behaviors of some traveling waves of system (1.1) partly depends on the relation () of the amplitude of wave and the level (deepness) of water. In the other words, their dynamic behavior vary with the changes of parameter ε, that is, the changes of ratio for the amplitude of wave and the deepness of water ℏ. In addition, compared with the research results of (1.3), the research results for (1.1) are few in the existing literatures. Thus, (1.1) is very necessary to be further studied.

It is worthy to mention that the solutions obtained by us in this paper are different from others in existing references, such as [9, 12–17, 29]. On the other hand, under different transformations, by using different methods, different results will be presented. In this paper, by using the integral bifurcation method [31], we will investigate different kinds of new traveling wave solutions of (1.1) and their dynamic properties under the translation-dilation transformation u(x, t) = v[1 + ϕ(x − vt)], ρ(x, t) = v[1 + ψ(x − vt)]. By the way, the integral bifurcation method possessed some advantages of the bifurcation theory of the planar dynamic system [32] and auxiliary equation method (see [33, 34] and references cited therein), it is easily combined with computer method [35] and useful for many nonlinear partial diffential equations (PDEs) including some PDEs with high power terms, such as K(m, n) equation [36]. So, by using this method, we will obtain some new traveling wave solutions of (1.1). Some interesting phenomena will be presented.

The rest of this paper is organized as follows. In Section 2, we will derive the two-dimensional planar system of (1.1) and its first integral equations. In Section 3, by using the integral bifurcation method, we will obtain some new traveling wave solutions of nonsingular type and singular type and investigate their dynamic behaviors.

2. The Two-Dimensional Planar System of (1.1) and Its First Integral Equations

Obviously, (1.1) can be rewritten as the following form

()

In order to change the PDE (2.1) into an ordinary differential equation, we make a transformation

()

where ξ = x − vt and v is an arbitrary nonzero constant. In fact, (2.2) is a translation-dilation transformation, it has been used extensively in many literatures. Its idea came from many existing references. For example, in [37], the expression u = λ^1/(m−l)U[λ^{(m−n)/2(m−l)}(x + λt)] is a dilation transformation. In [38], the expression U(x, t) = u(x − ωt) + ω is a translation transformation. In [39, 40], the expression z = (u − v)/|v| which was first used by Parkes and Vakhnenko is also a translation-dilation transformation.

After substituting (2.2) into (2.1), integrating them once yields

()

where the integral constant A ≠ 0 and ϕ^′ denotes ϕ_ξ. From the second equation of (2.3), we easily obtain

()

where ε ≠ 0. Substituting (2.4) into the first equation of (2.3), we obtain

()

where 𝔸 denotes (ε − 2 + εϕ).

Let ϕ^′ = dϕ/dξ = y. Thus (2.5) can be reduced to 2-dimensional planar system as follows:

()

where 𝔸 denotes (ε − 2 + εϕ).

Making a transformation

()

(2.6) becomes

()

where τ is a parameter. From the point of view of the geometric theory, the parameter τ is a fast variable, but the parameter ξ is a slow one. The system (2.8) is still a singular system through the system (2.6) becomes (2.8) by the transformation (2.7). This case is not same as that in [29]. Of course, as in [29], we can also change the system (2.6) into a regular system under another transformation dξ = (ε − 2 + εϕ) ³dτ. But we do not want to do that due to the following two reasons: (i) we need to keep the singularity of the original system; (ii) we need not to make any analysis of phase portraits as in [29].

Obviously, systems (2.6) and (2.8) have the same first integral as follows:

()

where h is an integral constant.

3. Traveling Wave Solutions of Nonsingular Type and Singular Type for (1.1) and Their Dynamic Behaviors

In this section, we will investigate different kinds of exact traveling wave solutions for (1.1) and their dynamic behaviors.

It is easy to know that (2.9) can be reduced to four kinds of simple equations when the parametric conditions satisfy the following four cases:

Case 1. A = ε − 2, h = 12σ(ε − 2)/ε²δ² and ε ≠ 0,2, v ≠ εκ/4(1 − ε).

Case 2. v = εκ/4(1 − ε), h = 12σ(ε − 2)/ε²δ² and ε ≠ 0,1, A ≠ ε − 2.

Case 3. A = ε − 2, h = 12σ(ε − 2)/ε²δ², v = εκ/4(1 − ε) and ε ≠ 0,1, 2.

Case 4. h = 12σ(2A+2−ε)²/ε²δ²(ε − 2).

We mainly aim to consider the new results of (1.1), so we only discuss the first two typical cases in this section. The other two cases can be similarly discussed, here we omit them.

3.1. The Exact Traveling Wave Solutions under Case 1

Under the parametric conditions A = ε − 2, h = 12σ(ε − 2)/ε²δ², v ≠ εκ/4(1 − ε) and ε ≠ 0 or 2, σ = ±1, (2.9) can be reduced to

()

where c = 3ε²/δ² ≥ 0, b = (3ε/δ²)[4(ε − 1) + εκ/v], a = (3/δ²)[4(1 − σ) + ε(3ε − 8) + εκ(ε − 2)/v]. Substituting (3.1) into the first expression in (2.8) yields

()

Write

()

The Δ = 0 if only if

. By using the exact solutions of (3.2), we can obtain different kinds of exact traveling wave solutions of parametric type of (1.1), see the following discussion.

(i)
If a > 0, then (3.2) has one exact solution as follows:
()
Substituting (3.4) into (2.7), and then integrating it yields
()
Substituting (3.4) into (2.2) and (2.4), then combining with (3.5), we obtain a couple of soliton-like solutions of (1.1) as follows:
()

()
(ii)
If a > 0, c > 0, Δ > 0, then (3.2) has one exact solution as follows:
()
Similarly, by using (3.8), (2.7), (2.2), and (2.4), we obtain two couples of soliton-like solutions of (1.1) as follows:
()
(iii)
If a > 0 and Δ < 0, then (1.1) has one couple of soliton-like solutions as follows:
()
(iv)
If a > 0 and c ≠ 0 (i.e., ε ≠ 0), then (1.1) has one couple of soliton-like solutions as follows:
()
(v)
If a > 0 and Δ = 0 (i.e. ), then (1.1) has one couple of kink and antikink wave solutions as follows:
()
(vi)
If a > 0 and b = 0 (i.e. κ = 4v(1/ε − 1)), then (1.1) has one couple of soliton-like solutions as follows:
()

In order to show the dynamic properties of above soliton-like solutions and kink and antikink wave solutions intuitively, as examples, we plot their graphs of some solutions, see Figures 1, 2, 3, and 4. Figures 1(a)–1(h) show the profiles of multiwaveform to solution the first solution of (3.6) for fixed parameters ϵ = 1, σ = −1, κ = 4, v = 4, δ = 5 and different ε-values. Figures 2(a)–2(d) show the profiles of multiwaveform to solution (3.7) for fixed parameters ϵ = 1, σ = −1, κ = 4, v = 3, δ = 5 and different ε-values. Figures 3(a)–3(d) show the profiles of multiwaveform to solution (3.9) for fixed parameters ϵ = −1, σ = −1, κ = −2, v = −4, δ = 3.5 and different ε-values. Figures 4(a)-4(b) show the profiles of kink wave solution (the first formula of (3.12)) for fixed parameters ϵ = 1, σ = −1, v = 0.4, δ = 3.5 and different (ε, κ)-values.

Details are in the caption following the image — **Figure 1 (a) Antikink wave**
Open in figure viewer PowerPoint

The profiles of multiwaveform of (3.6) for the given parameters and different ε-values: (a) ε = 1.2; (b) ε = 1.26; (c) ε = 1.4; (d) ε = 1.99; (e) ε = 2; (f) ε = 2.2; (g) ε = 3; (h) ε = 5.

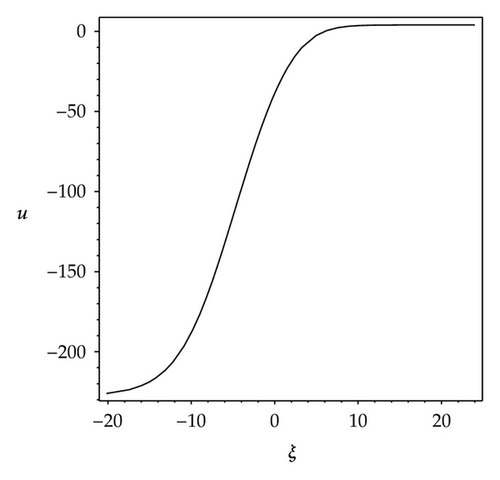
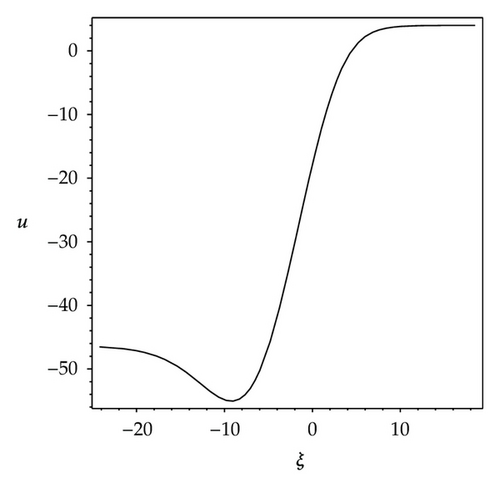
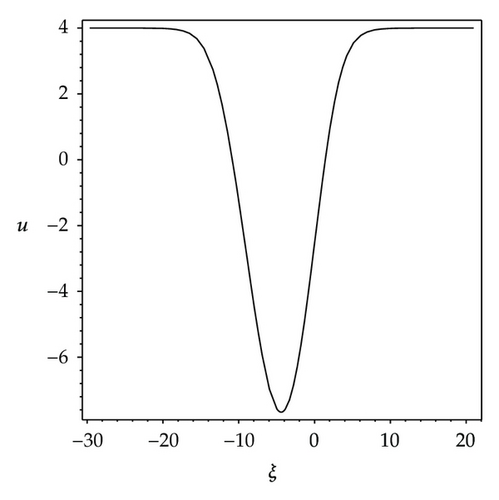
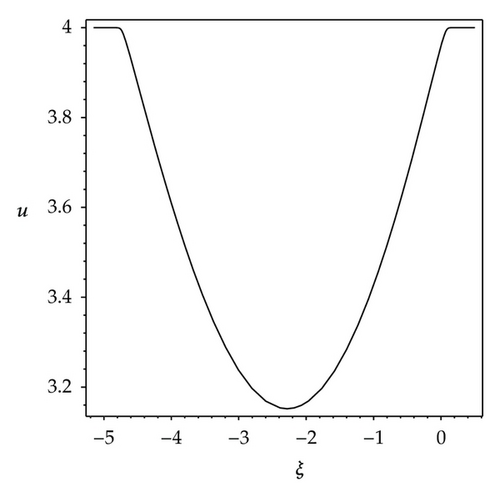
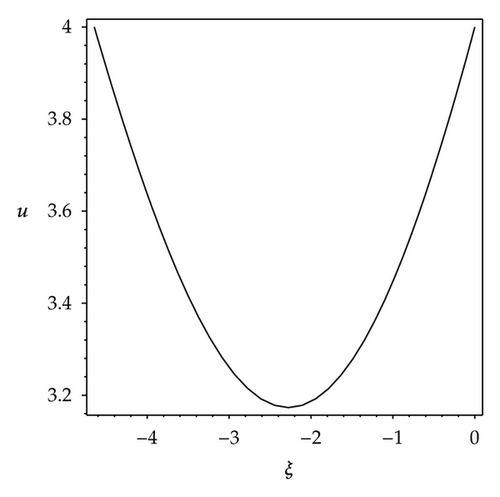
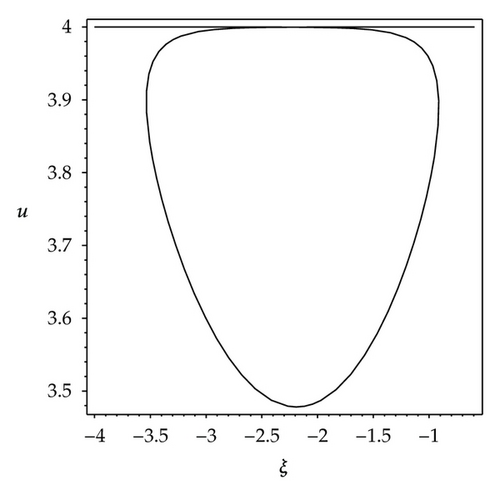
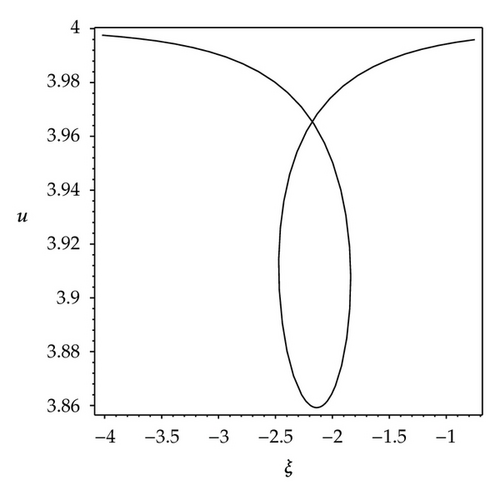
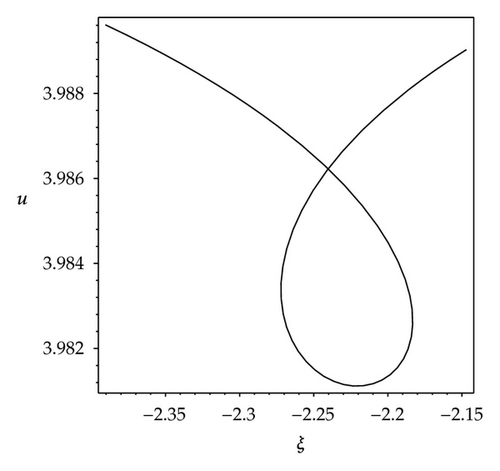
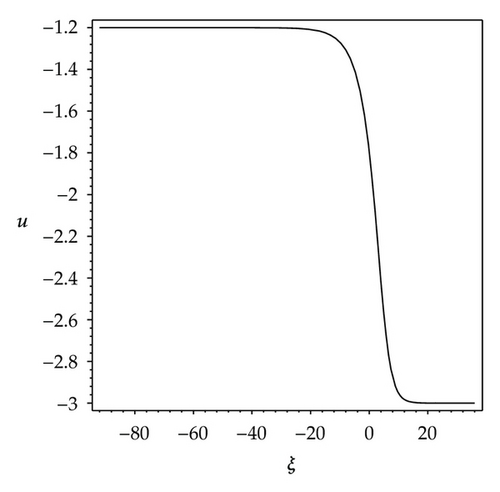
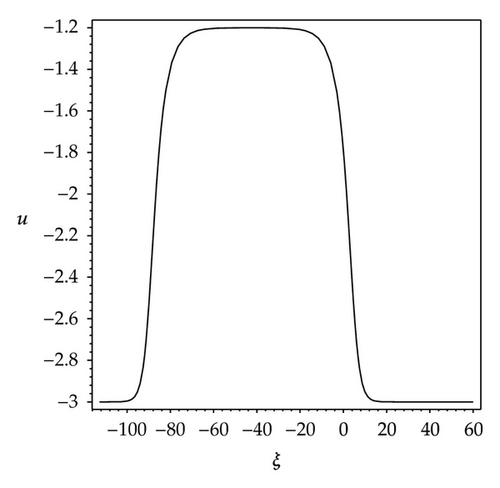
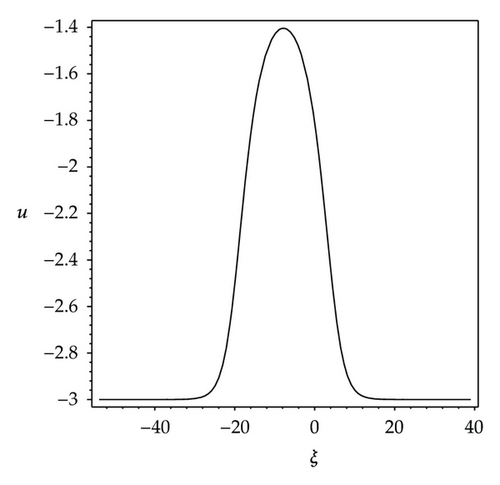
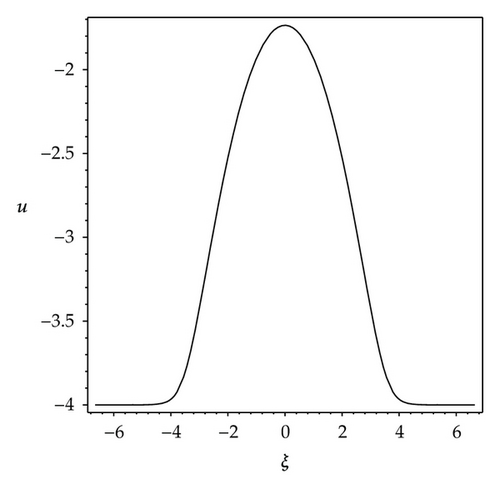
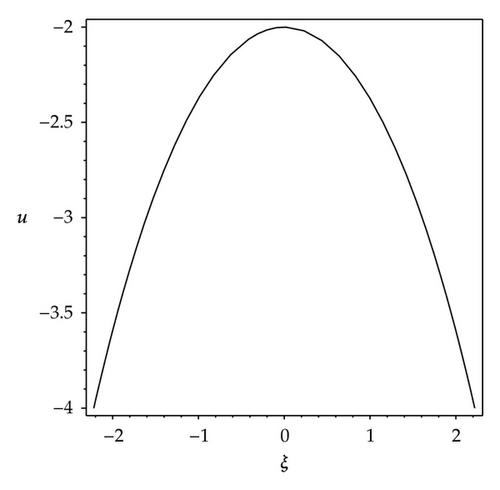
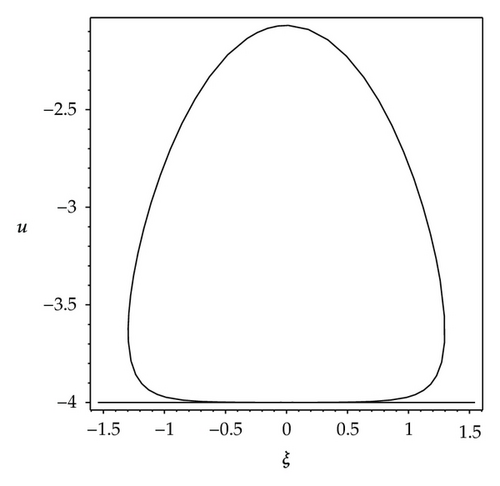
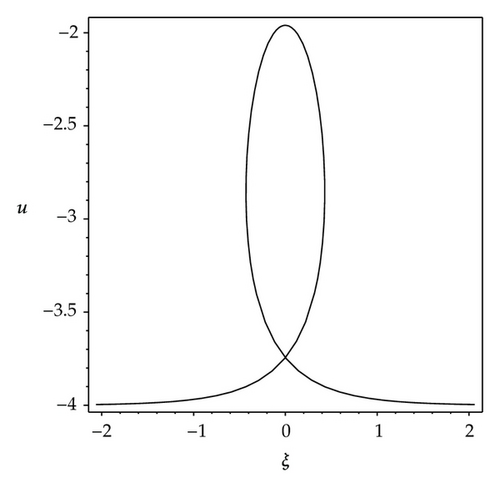
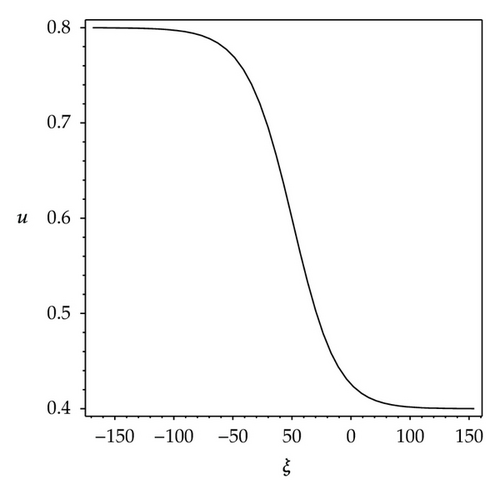
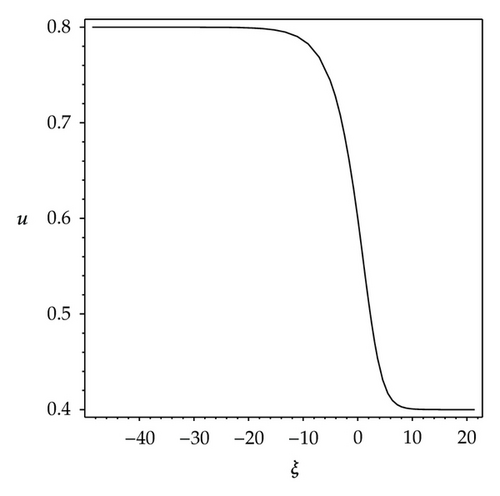
We observe that some profiles of above soliton-like solutions are very much sensitive to one of parameters, that is, their profiles are transformable (see Figures 1–3). But the others are not, their waveforms do not vary no matter how the parameters vary (see Figure 4). Some phenomena are very similar to those in [41, 42]. In [41], the waveforms of soliton-like solution of the generalized KdV equation vary with the changes of parameter and depend on the velocity c extremely. Similarly, in [42], the properties of some traveling wave solutions of the generalized KdV-Burges equation depend on the dissipation coefficient α; if dissipation coefficient α ≥ λ₁, it appears as a monotonically kink profile solitary wave; if 0 < α ≤ λ₁, it appears as a damped oscillatory wave.

From Figures 1(a)–1(h), it is easy to know that the profiles of solution (3.6) vary gradually, its properties depend on the parameter ε. When parametric values of ε increase from 1.2 to 5, the solution (3.6) has eight kinds of waveforms: Figure 1(a) shows a shape of antikink wave when ε = 1.2; Figure 1(b) shows a shape of transmutative antikink wave when ε = 1.6; Figure 1(c) shows a shape of thin and dark solitary wave when ε = 1.4; Figure 1(d) shows a shape of fat and dark solitary wave when ε = 1.99; Figure 1(e) shows a shape of compacton wave when ε = 2; Figure 1(f) shows a shape of fat loop soliton when ε = 2.2; the Figure 1(g) shows a shape of thin loop soliton when ε = 3; Figure 1(h) shows a shape of oblique loop soliton when ε = 5.

Similarly, from Figures 2(a)–2(d), it is also easy to know that the profiles of solution (3.7) are transformable, but their changes are not gradual, it depends on the parameter ε extremely. When parametric values of ε increase from 1.2 to 2.4, the solution (3.7) has four kinds of waveforms: Figure 2(a) shows a shape of smooth kink wave when ε = 1.2; Figure 2(b) shows a shape of fat and bright solitary wave when ε = 1.20000001; Figure 2(c) shows a shape of thin and bright solitary wave when ε = 1.22; Figure 2(d) shows a shape of singular wave of cracked loop soliton when ε = 2.4. Especially, the changes of waveforms from Figure 2(a) to Figure 2(b) and from Figure 2(c) to Figure 2(d) happened abruptly.

As in Figure 1, the profiles of the first solution of (3.9) in Figure 3 vary gradually. When parametric values of ε increase from 1.8 to 2.8, the waveform becomes a bright compacton from a shape of bright solitary wave, then becomes a shape of fat loop soliton and a shape of thin loop soliton at last.

Different from the properties of solutions (3.6), (3.7) and (3.9), the property of the first solution of (3.12) is stable. The profile of the first solution of (3.12) is not transformable no matter how the parameters vary. Both Figures 4(a) and 4(b) show a shape of smooth kink wave.

3.2. The Traveling Wave Solutions Under Case 2

Under the parametric conditions v = εκ/4(1 − ε), h = 12σ(ε − 2)/ε²δ² and ε ≠ 0 or 1, (2.9) becomes

()

where P = 3ε²/δ² > 0, Q = (−3/δ²)[4(σ + 1) + ε(ε − 4)], R = 48σA(ε − 2 − A)/ε²δ². Substituting (3.14) into the first expression in (2.8) yields

()

We know that the case σ = −1 corresponds to the situation in which the gravity acceleration points upwards. As an example, in this subsection, we only discuss the case σ = −1. The case σ = 1 can be similarly discussed, but we omit them here. Especially, when σ = −1, the above values of P, Q, R can be reduced to P = 3ε²/δ² > 0, Q = −3ε(ε − 4)/δ², R = 48A(A + 2 − ε)/ε²δ².

(i) If

then the P = m², Q = −(1 + m²), R = 1. Under these parametric conditions, (3.15) has a Jacobi elliptic function solution as follows:

()

where

is the model of Jacobi elliptic function and 0 < m < 1.

Substituting (3.16) and (3.17) into (2.7), respectively, we obtain

()

Substituting (3.16) into (2.2) and (2.4), using (3.18) and the transformation ξ = x − vt = x − (εκ/4(1 − ε))t, we obtain a couple of periodic solutions of (1.1) as follows:

()

Substituting (3.17) into (2.2) and (2.4), using (3.19) and the transformation ξ = x − vt = x − (εκ/4(1 − ε))t, we also obtain a couple of periodic solutions of (1.1) as follows:

()

(ii) If

, then the P = 1, Q = −(1 + m²), R = m². In the case of these parametric conditions, (3.15) has a Jacobi elliptic function solution as follows:

()

As in the first case (i) using the same method, we obtain a couple of periodic solutions of (1.1) as follows:

()

Especially, when m → 1 (i.e.,

), ns(τ, m) → coth(τ), sn(τ, m) → tanh(τ), cn(τ, m) → sech(τ), dn(τ, m) → sech(τ). From (3.23) and (3.24), we obtain a couple of kink-like solutions of (1.1) as follows:

()

(iii) If

, then the P = 1 − m², Q = 2m² − 1, R = −m². In the case of these parametric conditions, (3.15) has a Jacobi elliptic function solution as follows:

()

As in the first case (i), similarly, we obtain a couple of periodic solutions of (1.1) as follows:

()

where

(iv) If

, then the P = 1 − m², Q = 2 − m², R = 1. In the case of these parametric conditions, (3.15) has a Jacobi elliptic function solution as follows:

()

Similarly, we obtain a couple of periodic solutions of (1.1) as follows:

()

where

(v) If

, then the P = 1, Q = 2 − m², R = 1 − m². In the case of these parametric conditions, (3.15) has a Jacobi elliptic function solution as follows:

()

As in the first case (i) using the same method, we obtain a couple of periodic solutions of (1.1) as follows:

()

In order to show the dynamic properties of above periodic solutions intuitively, as examples, we plot their graphs of the solutions (3.20), (3.23) and (3.24), see Figures 5 and 6.

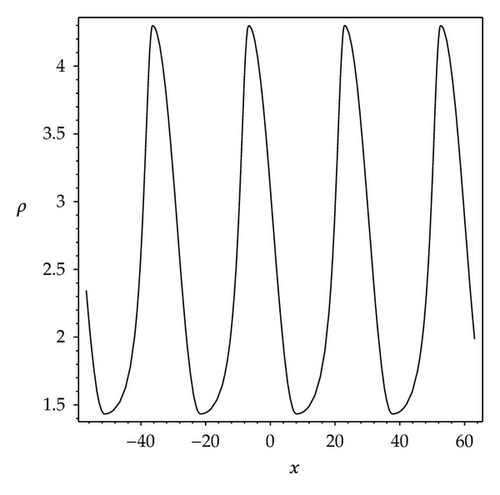
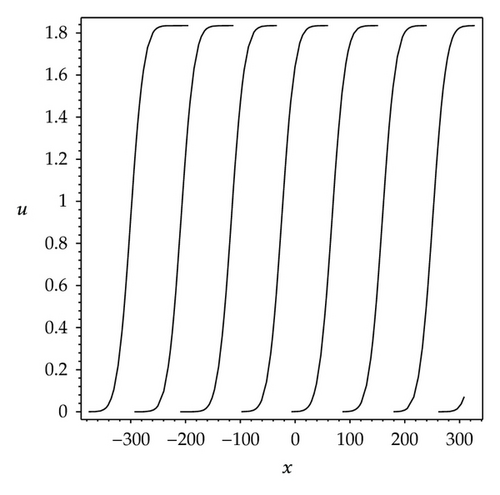
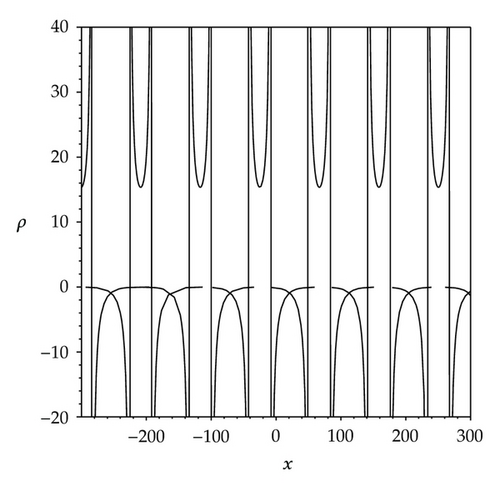
Figures 5(a) and 5(b) show two shapes of smooth and continuous periodic waves, all of them are nonsingular type. Figure 6(a) shows a shape of periodic kink wave. Figure 6(b) shows a shape of singular periodic wave. Both Figures 6(a) and 6(b) show two discontinuous periodic waves, all of them are singular type.

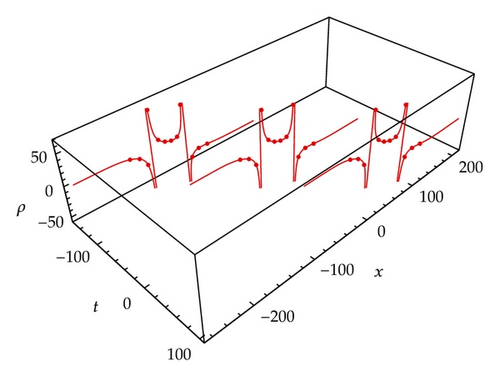
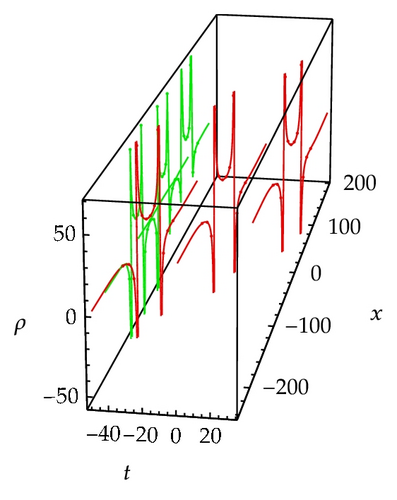
From the above illustrations, we find that the waveforms of some solutions partly depend on wave parameters. Indeed, in 2006, Vakhnenko and Parkes’s work [43] successfully explained similar phenomena. In [43], the graphical interpretation of the solution for gDPE is presented. In this analysis, the 3D-spiral (whether one loop from a spiral or a half loop of a spiral) has the different projections that is the essence of the possible solutions. Of caurse, this approach also can be employed to the 2-component Camassa-Holm shallow water system (1.1). By using the Vakhnenko and Parkes’s theory, the phenomena which appeared in this work are easily understood, so we omit this analysis at here. However, it is necessary to say something about the cracked loop soliton (Figure 2(d)) and the singular periodic wave (Figure 6(b)), what are the 3D-curves with projections associated with two peculiar solutions (3.7) and (3.24) which are shown in Figure 2(d) and Figure 6(b)? In order to answer this question, by using the Vakhnenko and Parkes’s approach, as an example we give the 3D-curves of solution (3.24) and their projection curve in the xoρ-plane, which are shown in Figure 7. For convenience to distinguish them, we colour the 3D-curves red and colour their projection curve green. From Figure 7, we can see that the 3D-curves are not intersected, but their projection curve is intersected in xoρ-plane.

4. Conclusion

In this work, by using the integral bifurcation method together with a translation-dilation transformation, we have obtained some new traveling wave solutions of nonsingular type and singular type of 2-component Camassa-Holm equation. These new solutions include soliton solutions, kink wave solutions, loop soliton solutions, compacton solutions, smooth periodic wave solutions, periodic kink wave solution, singular wave solution, and singular periodic wave solution. By investigating these new exact solutions of parametric type, we found some new traveling wave phenomena, that is, the waveforms of some solutions partly depend on wave parameters. For example, the waveforms of solutions (3.6), (3.7), and (3.9) vary with the changes of parameter. These are three peculiar solutions. The solution (3.6) has five kinds of waveforms, which contain antikink wave, transmutative antikink wave, dark soliton, compacton, and loop soliton according as the parameter ε varies. The solution (3.7) has three kinds of waveforms, which contain kink wave, bright soliton, and singular wave (cracked loop soliton) according as the parameter ε varies. The solution (3.9) also has three kinds of waveforms, which contain bright soliton, compacton, and loop soliton according as the parameter ε varies. These phenomena show that the dynamic behavior of these waves partly depends on the relation of the amplitude of wave and the level of water.

Acknowledgments

The authors thank reviewers very much for their useful comments and helpful suggestions. This work was financially supported by the Natural Science Foundation of China (Grant no. 11161020) and was also supported by the Natural Science Foundation of Yunnan Province (no. 2011FZ193).

References

1 Constantin A. and Ivanov R. I., On an integrable two-component Camassa-Holm shallow water system, Physics Letters A. (2008) 372, no. 48, 7129–7132, https://doi.org/10.1016/j.physleta.2008.10.050, 2474608, ZBL1227.76016.
10.1016/j.physleta.2008.10.050
CAS Web of Science® Google Scholar
2 Dullin H. R., Gottwald G. A., and Holm D. D., Camassa-Holm, Korteweg-de Vries-5 and other asymptotically equivalent equations for shallow water waves, Japan Society of Fluid Mechanics. (2003) 33, no. 1-2, 73–95, https://doi.org/10.1016/S0169%2D5983(03)00046%2D7, 1995028, ZBL1032.76518.
10.1016/S0169-5983(03)00046-7
Google Scholar
3 Johnson R. S., The Camassa-Holm equation for water waves moving over a shear flow, Fluid Dynamics Research. (2003) 33, no. 1-2, 97–111, https://doi.org/10.1016/S0169%2D5983(03)00036%2D4, 1995029, ZBL1032.76519.
10.1016/S0169-5983(03)00036-4
Web of Science® Google Scholar
4 Busuioc V., On second grade fluids with vanishing viscosity, Comptes Rendus de l′Académie des Sciences I. (1999) 328, no. 12, 1241–1246, https://doi.org/10.1016/S0764%2D4442(99)80447%2D9, 1701393, ZBL0935.76004.
10.1016/S0764-4442(99)80447-9
Web of Science® Google Scholar
5 Dai H.-H., Exact travelling-wave solutions of an integrable equation arising in hyperelastic rods, Wave Motion. (1998) 28, no. 4, 367–381, https://doi.org/10.1016/S0165%2D2125(98)00014%2D6, 1642422, ZBL1074.74541.
10.1016/S0165-2125(98)00014-6
Web of Science® Google Scholar
6 Johnson R. S., Camassa-Holm, Korteweg-de Vries and related models for water waves, Journal of Fluid Mechanics. (2002) 455, 63–82, https://doi.org/10.1017/S0022112001007224, 1894796, ZBL1037.76006.
10.1017/S0022112001007224
Web of Science® Google Scholar
7 Green A. E. and Naghdi P. M., Derivation of equations for wave propagation in water of variable depth, Journal of Fluid Mechanics. (1976) 78, no. 2, 237–246, 2-s2.0-0016876595, https://doi.org/10.1017/S0022112076002425, ZBL0351.76014.
10.1017/S0022112076002425
Web of Science® Google Scholar
8 Liu S.-Q. and Zhang Y., Deformations of semisimple bihamiltonian structures of hydrodynamic type, Journal of Geometry and Physics. (2005) 54, no. 4, 427–453, https://doi.org/10.1016/j.geomphys.2004.11.003, 2144711, ZBL1079.37058.
10.1016/j.geomphys.2004.11.003
Web of Science® Google Scholar
9 Chen M., Liu S.-Q., and Zhang Y., A two-component generalization of the Camassa-Holm equation and its solutions, Letters in Mathematical Physics A. (2006) 75, no. 1, 1–15, https://doi.org/10.1007/s11005%2D005%2D0041%2D7, 2207043, ZBL1105.35102.
10.1007/s11005-005-0041-7
Web of Science® Google Scholar
10 Ivanov R. I., Extended Camassa-Holm hierarchy and conserved quantities, Zeitschrift Fuer Naturforschung. (2006) 61, 133–138, ZBL1186.37079.
10.1515/zna-2006-3-404
CAS Google Scholar
11 Guan C. and Yin Z., Global existence and blow-up phenomena for an integrable two-component Camassa-Holm shallow water system, Journal of Differential Equations. (2010) 248, no. 8, 2003–2014, https://doi.org/10.1016/j.jde.2009.08.002, 2595712, ZBL1190.35039.
10.1016/j.jde.2009.08.002
Web of Science® Google Scholar
12 Guan C. and Yin Z., Global weak solutions for a two-component Camassa-Holm shallow water system, Journal of Functional Analysis. (2011) 260, no. 4, 1132–1154, https://doi.org/10.1016/j.jfa.2010.11.015, 2747018, ZBL1210.35209.
10.1016/j.jfa.2010.11.015
Web of Science® Google Scholar
13 Mustafa O. G., On smooth traveling waves of an integrable two-component Camassa-Holm shallow water system, Wave Motion. (2009) 46, no. 6, 397–402, https://doi.org/10.1016/j.wavemoti.2009.06.011, 2598637, ZBL1231.76063.
10.1016/j.wavemoti.2009.06.011
Web of Science® Google Scholar
14 Gui G. and Liu Y., On the global existence and wave-breaking criteria for the two-component Camassa-Holm system, Journal of Functional Analysis. (2010) 258, no. 12, 4251–4278, https://doi.org/10.1016/j.jfa.2010.02.008, 2609545, ZBL1189.35254.
10.1016/j.jfa.2010.02.008
Web of Science® Google Scholar
15 Guo Z., Asymptotic profiles of solutions to the two-component Camassa-Holm system, Nonlinear Analysis. Theory, Methods & Applications A. (2012) 75, no. 1, 1–6, https://doi.org/10.1016/j.na.2011.01.030, 2846775, ZBL1223.35275.
10.1016/j.na.2011.01.030
Web of Science® Google Scholar
16 Tian L., Xu Y., and Zhou J., Attractor for the viscous two-component Camassa-Holm equation, Nonlinear Analysis. Real World Applications. (2012) 13, no. 3, 1115–1129, https://doi.org/10.1016/j.nonrwa.2011.09.005, 2863941, ZBL1239.35143.
10.1016/j.nonrwa.2011.09.005
CAS Web of Science® Google Scholar
17 Yuen M., Perturbational blowup solutions to the 2-component Camassa-Holm equations, Journal of Mathematical Analysis and Applications. (2012) 390, no. 2, 596–602, https://doi.org/10.1016/j.jmaa.2011.05.016, 2890540, ZBL1236.35005.
10.1016/j.jmaa.2011.05.016
Web of Science® Google Scholar
18 Guo Z., Zhu M., and Ni L., Blow-up criteria of solutions to a modified two-component Camassa-Holm system, Nonlinear Analysis. Real World Applications. (2011) 12, no. 6, 3531–3540, https://doi.org/10.1016/j.nonrwa.2011.06.013, 2832990, ZBL1231.35200.
10.1016/j.nonrwa.2011.06.013
Web of Science® Google Scholar
19 Popowicz Z., A 2-component or N = 2 supersymmetric Camassa-Holm equation, Physics Letters A. (2006) 354, no. 1-2, 110–114, https://doi.org/10.1016/j.physleta.2006.01.027, 2220696.
10.1016/j.physleta.2006.01.027
CAS Web of Science® Google Scholar
20 Escher J., Kohlmann M., and Lenells J., The geometry of the two-component Camassa-Holm and Degasperis-Procesi equations, Journal of Geometry and Physics. (2011) 61, no. 2, 436–452, https://doi.org/10.1016/j.geomphys.2010.10.011, 2746128, ZBL1210.58007.
10.1016/j.geomphys.2010.10.011
Web of Science® Google Scholar
21 Escher J., Lechtenfeld O., and Yin Z., Well-posedness and blow-up phenomena for the 2-component Camassa-Holm equation, Discrete and Continuous Dynamical Systems A. (2007) 19, no. 3, 493–513, https://doi.org/10.3934/dcds.2007.19.493, 2335761, ZBL1149.35307.
10.3934/dcds.2007.19.493
Web of Science® Google Scholar
22 Guo Z. and Zhou Y., On solutions to a two-component generalized Camassa-Holm equation, Studies in Applied Mathematics. (2010) 124, no. 3, 307–322, https://doi.org/10.1111/j.1467%2D9590.2009.00472.x, 2655943, ZBL1189.35255.
10.1111/j.1467-9590.2009.00472.x
Web of Science® Google Scholar
23 Guo Z., Blow-up and global solutions to a new integrable model with two components, Journal of Mathematical Analysis and Applications. (2010) 372, no. 1, 316–327, https://doi.org/10.1016/j.jmaa.2010.06.046, 2672529, ZBL1205.35045.
10.1016/j.jmaa.2010.06.046
Web of Science® Google Scholar
24 Zhang P. and Liu Y., Stability of solitary waves and wave-breaking phenomena for the two-component Camassa-Holm system, International Mathematics Research Notices. (2010) 2010, no. 11, 1981–2021, https://doi.org/10.1093/imrn/rnp211, 2646352, ZBL1231.35184.
10.1093/imrn/rnp211
Web of Science® Google Scholar
25 Guo Z. and Ni L., Persistence properties and unique continuation of solutions to a two-component Camassa-Holm equation, Mathematical Physics, Analysis and Geometry. (2011) 14, no. 2, 101–114, https://doi.org/10.1007/s11040%2D011%2D9089%2Dz, 2802456, ZBL1245.35108.
10.1007/s11040-011-9089-z
Web of Science® Google Scholar
26 Guo Z. and Zhu M., Wave breaking for a modified two-component Camassa-Holm system, Journal of Differential Equations. (2012) 252, no. 3, 2759–2770, https://doi.org/10.1016/j.jde.2011.09.041, 2860639, ZBL1230.37093.
10.1016/j.jde.2011.09.041
Web of Science® Google Scholar
27 Camassa R. and Holm D. D., An integrable shallow water equation with peaked solitons, Physical Review Letters. (1993) 71, no. 11, 1661–1664, https://doi.org/10.1103/PhysRevLett.71.1661, 1234453, ZBL0972.35521.
10.1103/PhysRevLett.71.1661
CAS PubMed Web of Science® Google Scholar
28 Camassa R., Holm D. D., and Hyman J. M., A new integrable shallow water equation, Advances in Applied Mechanics. (1994) 31, 1–33, 2-s2.0-56349110516, https://doi.org/10.1016/S0065%2D2156(08)70254%2D0, ZBL0808.76011.
10.1016/S0065-2156(08)70254-0
Google Scholar
29 Li J. B. and Li Y. S., Bifurcations of travelling wave solutions for a two-component Camassa-Holm equation, Acta Mathematica Sinica. (2008) 24, no. 8, 1319–1330, https://doi.org/10.1007/s10114%2D008%2D6207%2D3, 2438303, ZBL1182.34064.
10.1007/s10114-008-6207-3
Web of Science® Google Scholar
30 Lin J., Ren B., Li H.-M., and Li Y.-S., Soliton solutions for two nonlinear partial differential equations using a Darboux transformation of the Lax pairs, Physical Review E. (2008) 77, no. 3, 036605, https://doi.org/10.1103/PhysRevE.77.036605, 2495450.
10.1103/PhysRevE.77.036605
Web of Science® Google Scholar
31 Rui W., He B., Long Y., and Chen C., The integral bifurcation method and its application for solving a family of third-order dispersive PDEs, Nonlinear Analysis. Theory, Methods & Applications A. (2008) 69, no. 4, 1256–1267, https://doi.org/10.1016/j.na.2007.06.027, 2426689, ZBL1144.35461.
10.1016/j.na.2007.06.027
Web of Science® Google Scholar
32 Li J. and Liu Z., Smooth and non-smooth traveling waves in a nonlinearly dispersive equation, Applied Mathematical Modelling. (2000) 25, no. 1, 41–56, 2-s2.0-0034317577, https://doi.org/10.1016/S0307%2D904X(00)00031%2D7, ZBL0985.37072.
10.1016/S0307-904X(00)00031-7
PubMed Web of Science® Google Scholar
33 Hu J., An algebraic method exactly solving two high-dimensional nonlinear evolution equations, Chaos, Solitons and Fractals. (2005) 23, no. 2, 391–398, https://doi.org/10.1016/j.chaos.2004.02.044, 2089566, ZBL1069.35065.
10.1016/j.chaos.2004.02.044
Web of Science® Google Scholar
34 Yomba E., The extended F-expansion method and its application for solving the nonlinear wave, CKGZ, GDS, DS and GZ equations, Physics Letters A. (2005) 340, no. 1–4, 149–160, 2-s2.0-19444369705, https://doi.org/10.1016/j.physleta.2005.03.066, ZBL1145.35455.
10.1016/j.physleta.2005.03.066
CAS Web of Science® Google Scholar
35 Rui W., Long Y., He B., and Li Z., Integral bifurcation method combined with computer for solving a higher order wave equation of KdV type, International Journal of Computer Mathematics. (2010) 87, no. 1–3, 119–128, https://doi.org/10.1080/00207160801965321, 2598729, ZBL1182.65161.
10.1080/00207160801965321
Web of Science® Google Scholar
36 Wu X., Rui W., and Hong X., Exact traveling wave solutions of explicit type, implicit type, and parametric type for K(m, n) equation, Journal of Applied Mathematics. (2012) 2012, 23, 236875, https://doi.org/10.1155/2012/236875, 2904530.
10.1155/2012/236875
Google Scholar
37 Rosenau P., On solitons, compactons, and Lagrange maps, Physics Letters A. (1996) 211, no. 5, 265–275, https://doi.org/10.1016/0375%2D9601(95)00933%2D7, 1377202, ZBL1059.35524.
10.1016/0375-9601(95)00933-7
CAS Web of Science® Google Scholar
38 Dai H.-H. and Li Y., The interaction of the ω-soliton and ω-cuspon of the Camassa-Holm equation, Journal of Physics A. (2005) 38, no. 42, L685–L694, https://doi.org/10.1088/0305%2D4470/38/42/L04, 2186197.
10.1088/0305-4470/38/42/L04
Google Scholar
39 Parkes E. J. and Vakhnenko V. O., Explicit solutions of the Camassa-Holm equation, Chaos, Solitons & Fractals. (2005) 26, no. 5, 1309–1316, https://doi.org/10.1016/j.chaos.2005.03.011, 2149316, ZBL1072.35156.
10.1016/j.chaos.2005.03.011
Web of Science® Google Scholar
40 Vakhnenko V. O. and Parkes E. J., Periodic and solitary-wave solutions of the Degasperis-Procesi equation, Chaos, Solitons & Fractals. (2004) 20, no. 5, 1059–1073, https://doi.org/10.1016/j.chaos.2003.09.043, 2029379, ZBL1049.35162.
10.1016/j.chaos.2003.09.043
Web of Science® Google Scholar
41 Rui W., Chen C., Yang X., and Long Y., Some new soliton-like solutions and periodic wave solutions with loop or without loop to a generalized KdV equation, Applied Mathematics and Computation. (2010) 217, no. 4, 1666–1677, https://doi.org/10.1016/j.amc.2009.09.036, 2727410, ZBL1203.35242.
10.1016/j.amc.2009.09.036
Google Scholar
42 Zhang W. and Li X., Approximate damped oscillatory solutions for generalized KdV-Burgers equation and their error estimates, Abstract and Applied Analysis. (2011) 2011, 26, 807860, https://doi.org/10.1155/2011/807860, 2835261, ZBL1228.35211.
10.1155/2011/807860
Google Scholar
43 Vakhnenko V. O. and Parkes E. J., The solutions of a generalized Degasperis-Procesi equation, Reports of the National Academy of Sciences of Ukraine. (2006) no. 8, 88–94, 2312520.
Google Scholar

Citing Literature

All articles

Integral Bifurcation Method together with a Translation-Dilation Transformation for Solving an Integrable 2-Component Camassa-Holm Shallow Water System

Abstract

1. Introduction

2. The Two-Dimensional Planar System of (1.1) and Its First Integral Equations

3. Traveling Wave Solutions of Nonsingular Type and Singular Type for (1.1) and Their Dynamic Behaviors

3.1. The Exact Traveling Wave Solutions under Case 1

3.2. The Traveling Wave Solutions Under Case 2

4. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Information

About Wiley Online Library

Help & Support

Opportunities

Connect with Wiley

Integral Bifurcation Method together with a Translation-Dilation Transformation for Solving an Integrable 2-Component Camassa-Holm Shallow Water System

Abstract

1. Introduction

2. The Two-Dimensional Planar System of (1.1) and Its First Integral Equations

3. Traveling Wave Solutions of Nonsingular Type and Singular Type for (1.1) and Their Dynamic Behaviors

3.1. The Exact Traveling Wave Solutions under Case 1

3.2. The Traveling Wave Solutions Under Case 2

4. Conclusion

Acknowledgments

References

Citing Literature

Figures

References

Related

Information