Journal of Applied Mathematics
Volume 2012, Issue 1 734521
Research Article
Open Access

Analysis of the Elastic Large Deflection Behavior for Metal Plates under Nonuniformly Distributed Lateral Pressure with In-Plane Loads

Jeom Kee Paik, 

Corresponding Author

Jeom Kee Paik

The Ship and Offshore Research Institute, The Lloyd’s Register Educational Trust Research Centre of Excellence, Pusan National University, Busan 609-735, Republic of Korea pusan.ac.kr

Search for more papers by this author
Ju Hye Park, 

Ju Hye Park

The Ship and Offshore Research Institute, The Lloyd’s Register Educational Trust Research Centre of Excellence, Pusan National University, Busan 609-735, Republic of Korea pusan.ac.kr

Search for more papers by this author
Bong Ju Kim, 

Bong Ju Kim

The Ship and Offshore Research Institute, The Lloyd’s Register Educational Trust Research Centre of Excellence, Pusan National University, Busan 609-735, Republic of Korea pusan.ac.kr

Search for more papers by this author
First published: 03 October 2012
https://doi.org/10.1155/2012/734521
Citations: 3
Academic Editor: Carl M. Larsen

Abstract

The Galerkin method is applied to analyze the elastic large deflection behavior of metal plates subject to a combination of in-plane loads such as biaxial loads, edge shear and biaxial inplane bending moments, and uniformly or nonuniformly distributed lateral pressure loads. The motive of the present study was initiated by the fact that metal plates of ships and ship-shaped offshore structures at sea are often subjected to non-uniformly distributed lateral pressure loads arising from cargo or water pressure, together with inplane axial loads or inplane bending moments, but the current practice of the maritime industry usually applies some simplified design methods assuming that the non-uniform pressure distribution in the plates can be replaced by an equivalence of uniform pressure distribution. Applied examples are presented, demonstrating that the current plate design methods of the maritime industry may be inappropriate when the non-uniformity of lateral pressure loads becomes more significant.

1. Introduction

Ships and ship-shaped offshore structures are composed of metal plate elements, and the accurate computation of nonlinear behavior of the plate elements in deck, bottom and side shells up to the ultimate limit state is a basic requirement for the structural safety assessment. The plate elements in ships and ship-shaped offshore structures are generally subjected to combined inplane and lateral pressure loads. Inplane loads include biaxial compression/tension, biaxial inplane bending and edge shear, as shown in Figure 1, which are mainly induced by overall hull girder bending and/or torsion of the vessel. Lateral pressure loads are due to water pressure and/or cargo. In rough weather, roll and/or pitch motions of vessels are typical as shown in Figure 2, and, subsequently, the distribution of lateral pressure loads often becomes non-uniform as shown in Figure 3. For simplicity, however, the maritime industry usually applies a simplified design method in which the non-uniform distribution of lateral pressure loads is replaced by an equivalence of uniformly distributed lateral pressure loads with an average magnitude of applied pressure loads.

Details are in the caption following the image
Figure 1
Open in figure viewerPowerPoint
In-plane load components applied in a plate element.
Details are in the caption following the image
Figure 2
Open in figure viewerPowerPoint
Roll motion of a vessel causing nonuniformity of lateral pressure load distribution in the hull cross-section.
Details are in the caption following the image
Figure 3
Open in figure viewerPowerPoint
Non-uniformly distributed lateral pressure loads in a plate element.

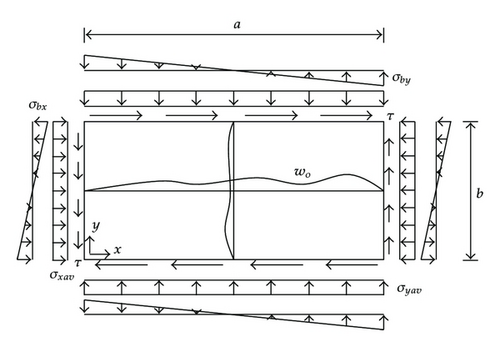
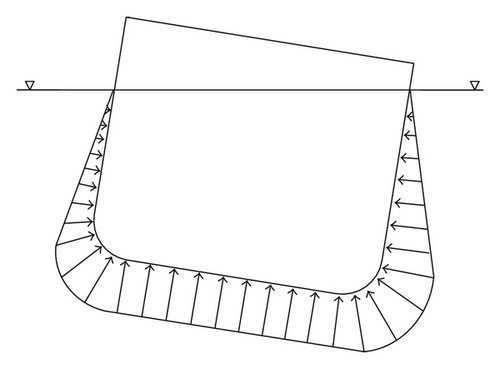
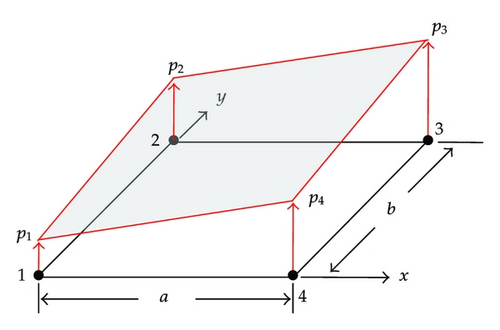
A large number of studies have been available in the literature, for example [1–6]. In the present paper, a mathematical algorithm is derived to analyze the elastic large deflection behavior, including buckling and postbuckling response, of plate elements under combined inplane and lateral pressure loads noted previously, with the emphasis on the non-uniformly distributed lateral pressure loads. The Galerkin method is applied to solve the nonlinear governing differential equations of elastic large deflection plate theory for plate elements. In the literature, the studies of metal plate buckling are also available, for example [7–13].

2. Elastic Large Deflection Analysis

The elastic large deflection behavior of a plate element with initial imperfections can be analyzed by solving two differential equations, one representing the equilibrium condition and the other representing the compatibility condition [5]:
()
()
Once the Airy stress function F is defined, the membrane stress components at a certain position inside the plate may be expressed as follows:
()
()
()
To apply the Galerkin method for solving the nonlinear governing differential equations, the added deflection w and initial deflection wo are assumed as follows:
()
()
where fm(x) and gn(y) are functions which satisfy the boundary conditions for the plate. Amn and Aomn are unknown and known deflection coefficients, respectively.
Equations (2.4) and (2.5) are substituted into (2.2) to obtain the stress function F. In this case, the particular solution FP of the stress function can be expressed as follows:
()
where the coefficients Krs will be second-order functions with regard to the unknown deflection coefficients Amn.
With the homogeneous solution FH of the stress function which satisfies the applied loading condition, the complete stress function F may be given by
()
To compute the unknown coefficients Amn, the Galerkin method is applied to the equilibrium equation (2.1), resulting in the following equation:
()
Equations (2.4), (2.5), and (2.7) into (2.8), and performing the integration over the whole volume of the plate, a set of third-order simultaneous equations with regard to the unknown coefficients Amn will be obtained.

3. Application to the Elastic Large Deflection Analysis of Simply Supported Plates

In the present paper, the procedure described in [5] is applied. It is assumed that the plate element is simply supported along the four edges where support members such as longitudinal stiffeners and transverse frames are located. The simply supported edge conditions for the plates should satisfy the following conditions
()
()
To satisfy the boundary condition, the added deflection function w and the initial deflection wo can be assumed in Fourier series:
()
()
where Amn and Aomn are the unknown and the known coefficients, respectively. The condition of combined loads, namely biaxial loads, biaxial inplane bending and edge shear and lateral pressure loads are given as follows:
()
()
()
()
()
For simplicity in expressing the various functions, the following abbreviations are involving sine or cosine terms:
()
To find the stress function F which should satisfy (2.2), (3.2) and (3.3) are substituted into (2.2) and the following equation yields:
()
A particular solution FP for the Airy stress function can be obtained as follows:
()
Equation (3.7) is substituted into (2.2), the coefficients B1, B2, B3 and B4, as follows:
()
Equation (3.8) is substituted into (3.7), and a particular solution FP is obtained as follows:
()
By considering the condition of load application, the homogeneous solution FH for the stress function is given by
()
The Airy stress function F is then expressed by the sum of the particular and homogeneous solution as follows:
()
To compute the unknown coefficientsAmn, the Galerkin method is applied to (2.1) as follows:
()
Substitution of (3.11) into (2.1) and then (2.1) to (3.12) after a derivation, a set of third order simultaneous equations for the unknown deflection coefficients Amn is obtained, as follows:
()
where q = lateral pressure loads, and the coefficients R1 to R16 and F1 to F5 are given in Appendix.
In (3.13), lateral pressure q will take the following form in general.
()
When uniform pressure loads are applied, that is, with p1 = p2 = p3 = p4, q = p1 is taken as constant value.

4. Applied Examples and Discussion

Some applied examples are now presented. A simply supported rectangular plate of a × b × t = 1660 mm × 830 × 16 mm under uniaxial compression and lateral pressure loads is considered, in which lateral pressure loads are applied first, followed by the monotonical application of axial compressive loads. The elastic modulus and Poisson’s ratio are E = 205.8 GPa and ν = 0.3. The elastic buckling strength σxE of this plate under uniaxial compression in the x direction is determined as follows:
()
where k = buckling coefficient which is taken as k= 4.
Also, the lateral pressure loads are taken as p1 = p2 = pa and p3 = p4 = pb in the present examples. The initial deflection of the plate is selected as follows (see Figure 4):
()
where A021 = 0.05t.
Details are in the caption following the image
Figure 4
Open in figure viewerPowerPoint
Configuration of the initial deflection in the plate.
The added deflection of the plate due to applied loads can be expressed as follows.
()
In the present study, the maximum number of amplitudes in the shorter direction of the plate is assumed as N = 1, but that in the longer direction of the plate is varied to investigate the best selection of M in terms of the accuracy and efficiency of the computations.

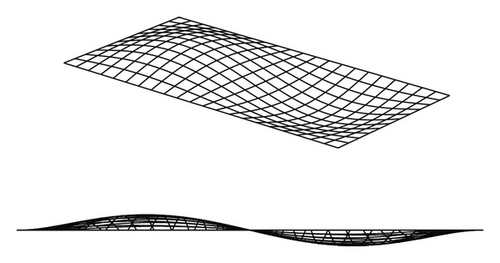
Figures 5(a) to 5(d) present the relation between the axial compressive loads versus total deflection at the center of the plate, that is, at x = a/2 and y = b/2, where the magnitude of lateral pressure loads and the maximum number of deflection amplitudes are varied. It is found that M = 5 may be sufficient enough in terms of accuracy and efficiency of the resulting computations. Table 1 represents the deformed shapes of the plate with different magnitudes or shapes of lateral pressure loads when σxav/σxE = 0 or 1.2 where M = 5 is taken. It is observed that the deflection modes of the plate are changed due to the application of axial compressive loads. This is because the plate tends to deflect as per the original buckling pattern associated with axial compressive loads.

Table 1. Deformed shapes of the plate when M = 5.

pa 

(MPa)

pb 

(MPa)

 σxav/σxE = 0.0 σxav/σxE = 1.2
0.1 0.1 image image
  
0.1 0.15 image image
  
0.1 0.2 image image
  
0.1 0.3 image image
  
0.1 0.4 image image
Details are in the caption following the image
Figure 5 (a)
Open in figure viewerPowerPoint
(a) The axial compressive load versus total deflection curves at pa = pb = 0.1 MPa. (b) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.15 MPa. (c) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.2 MPa. (d) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.3 MPa.
Details are in the caption following the image
Figure 5 (b)
Open in figure viewerPowerPoint
(a) The axial compressive load versus total deflection curves at pa = pb = 0.1 MPa. (b) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.15 MPa. (c) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.2 MPa. (d) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.3 MPa.
Details are in the caption following the image
Figure 5 (c)
Open in figure viewerPowerPoint
(a) The axial compressive load versus total deflection curves at pa = pb = 0.1 MPa. (b) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.15 MPa. (c) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.2 MPa. (d) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.3 MPa.
Details are in the caption following the image
Figure 5 (d)
Open in figure viewerPowerPoint
(a) The axial compressive load versus total deflection curves at pa = pb = 0.1 MPa. (b) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.15 MPa. (c) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.2 MPa. (d) The axial compressive load versus total deflection curves at pa = 0.1 MPa and pb = 0.3 MPa.

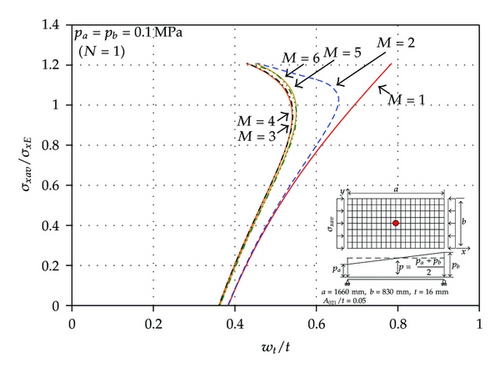
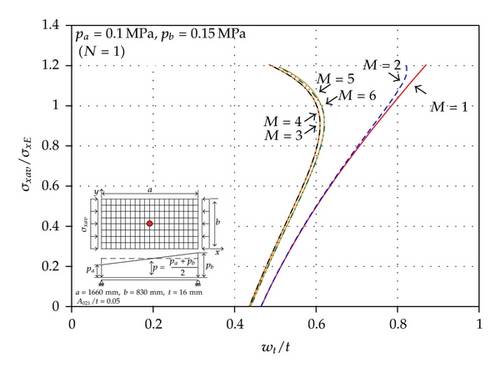
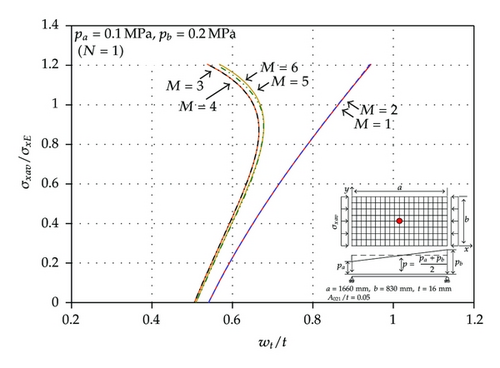
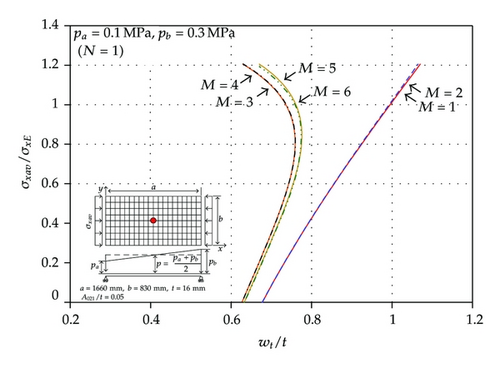
Figure 6 presents a comparison of the elastic large deflection responses of the plate between non-uniform and uniform pressure loads, the latter being taken as the average value of the pressure loads as per the current practice of the maritime industry.

Details are in the caption following the image
Figure 6
Open in figure viewerPowerPoint
The axial compressive loads versus total deflection at x = 3a/4 and y = b/2.

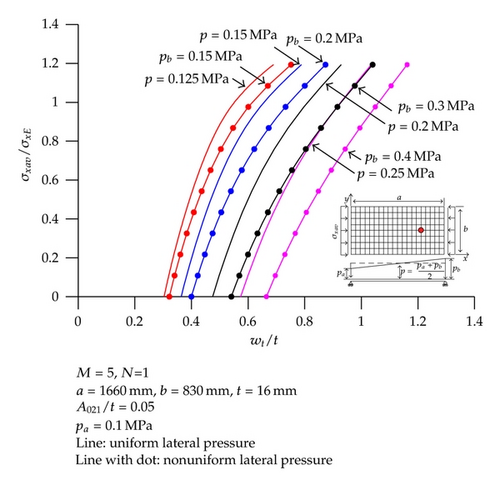
It is found that the current practice of the maritime industry with an average magnitude of applied pressure loads underestimates the lateral deflection of the plate compared to the real condition of the pressure load application, that is, with a non-uniform distribution. The difference between the two cases becomes larger and larger as the non-uniformity of lateral pressure loads becomes more significant.

The underestimation of the plate deflection due to external pressure loads gives rise to the overestimation of plate strength performance which may lead to unsafe design at optimistic side.

5. Concluding Remarks

The aim of the present paper has been to analyze the elastic large deflection behavior of metal plates subject to combined inplane and lateral pressure loads. When lateral pressure loads applied in plate elements are non-uniform, the current practice of the maritime industry applies some simplified design methods in which the non-uniform pressure distribution in the plates is replaced by an equivalence of uniform pressure distribution.

In the present paper, the Galerkin method was used to solve the nonlinear governing differential equations of plate elements under non-uniformly distributed lateral pressure loads in addition to inplane loads. Some applied examples are presented, demonstrating that the current practice of the maritime industry, that is, with an average magnitude of applied pressure loads as an equivalence, results in a great underestimation of lateral deflection calculations when the non-uniformity of lateral pressure loads becomes more significant. The underestimation of the plate deflection may lead to unsafe design of plates at optimistic side.

Thin plates buckle in elastic regime, while stocky plates may buckle in elastic-plastic or plastic regime. The present paper deals with elastic behavior only, and further studies are then recommended to take into account the effect of plasticity which is dominant in thick plates. Also, it is highly desirable for practical design purpose to develop a simpler method or design formulation.

Nomenclature

  • a:
  • Length of the plate
  • b:
  • Breadth of the plate
  • D:
  • Plate bending rigidity  ( = Et3/12(1 − ν2))
  • E:
  • Young’s modulus
  • F:
  • Airy’s stress function
  • M, N:
  • Maximum half-wave number of the assumed added deflection function in the x and y directions
  • Mx:
  • In-plane bending moment in the x direction ( = σbxt)
  • My:
  • In-plane bending moment in the y direction ( = σbyt)
  • p:
  • Lateral (out-of-plane) pressure load on the surface area
  • Px:
  • Axial force in the x direction ( = σxavbt)
  • Py:
  • Axial force in the y direction ( = σyavat)
  • t:
  • Thickness of the plate
  • w:
  • (Added) deflection of the plate due to the action of external loads
  • wo:
  • Initial deflection of the plate
  • wt:
  • Total deflection of the plate
  • z:
  • Axis direction normal to the xy plane
  • α:
  • Aspect ratio of the plate ( = a/b)
  • ν:
  • Poisson’s ratio
  • σbx,  σby:
  • Bending stresses in the x and y directions
  • σx, σy:
  • Normal stresses in the x and y directions
  • σxav,  σyav:
  • Mean stresses in the x and y directions
  • τ = τxy:
  • Shear stress.

    • Acknowledgments

    This research was supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Education, Science and Technology (Grant no. K20903002030-11E0100-04610).

      Appendix

      The coefficients R1 to R16 and F1 to F5 are given as follows:
      ()

        The full text of this article hosted at iucr.org is unavailable due to technical difficulties.