Data Reconstruction for a Disturbed Soil-Column Experiment Using an Optimal Perturbation Regularization Algorithm

1. Introduction

Soil and groundwater pollution has become a serious threat to sustainable development throughout the world. It is important to characterize physical/chemical reactions quantitatively for a solute transport process in the soils and groundwater (see [1–4], e.g.). To understand transport behaviors of the soil in the presence of infiltrating contaminants, soil column experiments are often performed in the laboratory. There are disturbed and undisturbed soil-column infiltrating experiments, and the soil-column in a disturbed experiment is often loaded uniformly and orderly with a lucite tube. The primary purpose of doing a disturbed soil-column experiment is to simulate and study transport behavior of the considered ion when it vertically penetrating through the column with artificial chemical liquid.

On the research of soil-column experiments in the known literatures we have, 1D case is often concerned with. In early studies, it is a main task to construct mathematical models for soil-column experiments. The typical works could belong to Nielsen and van Genuchten and their researching groups. Nielsen et al. (see [5], e.g.) gave a general advection-dispersion equation describing solute transport in unsaturated soils, and van Genuchten and Wagenet (see [6], e.g.) discussed solute transport models of two sites/two regions in the soils. With development of computational tools and techniques, numerical methods and software packages based on convection-dispersion equations are widely utilized in the research of soil-column infiltrating experiments (see [7–13], e.g.). Recently, the authors have ever considered an undisturbed soil-column experiment using a linear model (see [14]) and a nonlinear model (see [15]), respectively, and gave successful numerical inversions by utilizing the optimal perturbation algorithm based on the measured breakthrough data.

As we know, for a disturbed soil-column infiltrating experiment, there always has no more complicated physical/chemical reactions in the solute transport process, and then a mathematical model seems to be easy to establish due to linearity of the transportation. However, it is still a trouble on how to uniquely determine transport parameters in the model which can not be measured directly by the experiment. Another thing is how to work out the unknown parameters with high precision as much as possible. Thus, inverse problem and inversion analysis methods are often encountered with for solutes transport problems in soil-column infiltrating experiments.

In this paper, we will investigate a disturbed soil-column experiment carried out in Zibo, Shandong Province, China, and study transport behaviors of eight kinds of ions of Ca²⁺, Na⁺, Mg²⁺, K⁺, $$, $$, $$, and Cl⁻ by the inversion method. On the basis of advection-dispersion mechanism and hydrochemical analysis to the experimental data, two kinds of models describing their transport behaviors in the column are discussed respectively. By applying the optimal perturbation regularization algorithm, all unknown transport parameters for each ion are determined, and then the measured breakthrough data are reconstructed successfully. The inversion results show that the reconstruction data basically coincide with the measured breakthrough data, and the advection dispersion equation with suitable time-dependent reaction terms can be utilized to describe the experimental process and reconstruct the experimental data. The paper is arranged as follows.

Section 2 gives the soil-column experiment, breakthrough curves of the eight ions and preliminary analysis of their transport behaviors. In Section 3, two kinds of transport models are given respectively, one is suitable for $$, $$, and K⁺, and the other is for the rest. With the help of the models, the parameter identification problem for each ion is set forth based on the breakthrough data, and an optimal perturbation regularization algorithm is introduced. In Section 4, all the unknowns for each considered ion are determined by the inversion algorithm, and the breakthrough data are reconstructed. Finally, conclusions and discussions on the real problem here are presented.

2. Experimental Analysis

The disturbed soil-column experiment was carried out in a simple apparatus in a lab in Shandong University of Technology. The device is installed with three systems which are infiltrating system, soil-column system, and sample collector system, respectively. The soil column is composed by fine sands with diameter of 2 [mm], the diameter of the lucite tube loading the column is 18.6 [cm], and the height of the column is about 62 [cm]. After infiltrating the column with distilled water for 24 hours, the experiment was performed by infiltrating into the column with artificial coalmine water at the temperature of 20 centigrade.

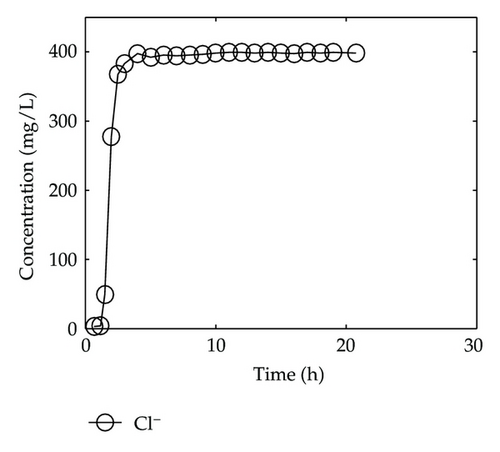
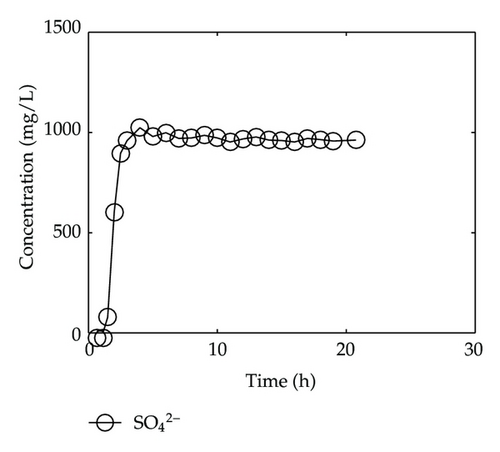
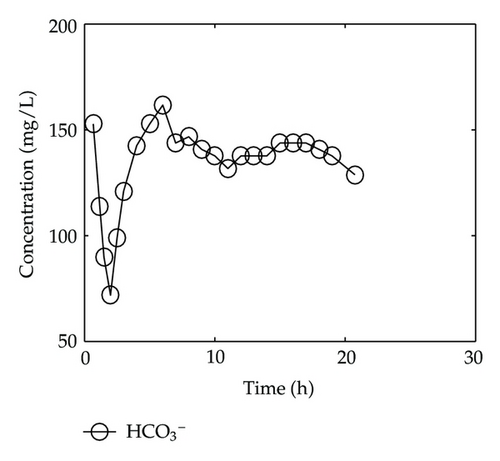
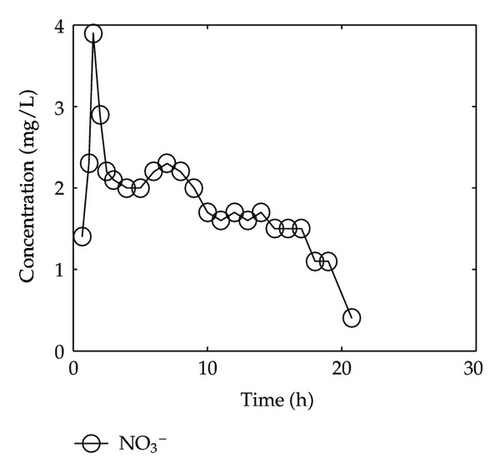
By collecting water samples at the bottom of the column, 23 samples were collected, and all of them were immediately sent to tested and analyzed in Shandong General Inspecting Station of Geology and Environment. Thus, we get the so-called breakthrough data of positive ions of Ca²⁺, Na⁺, K⁺, and Mg²⁺ and negative ions of Cl⁻, $$, $$, and $$, which are plotted in Figure 1 and Figure 2, respectively, where the transverse axis denotes the experimental time [h], and the vertical axis represents concentration of the solute ion at the bottom of the column [mg/L].

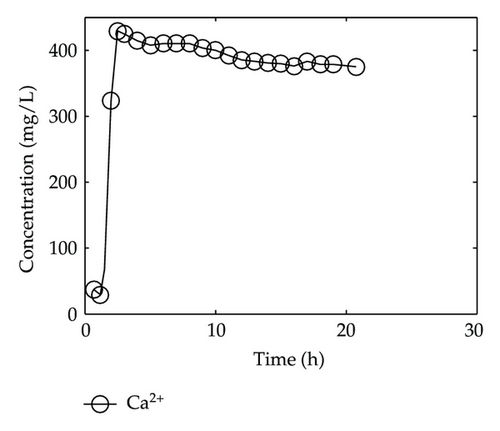
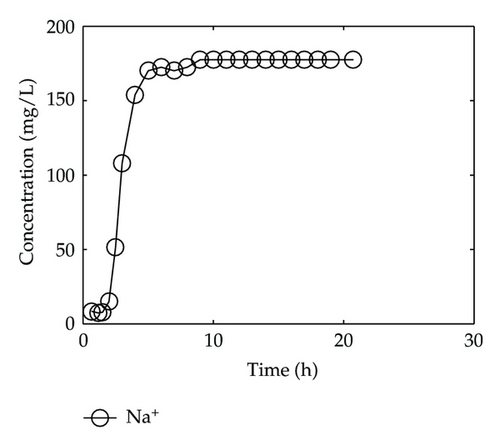
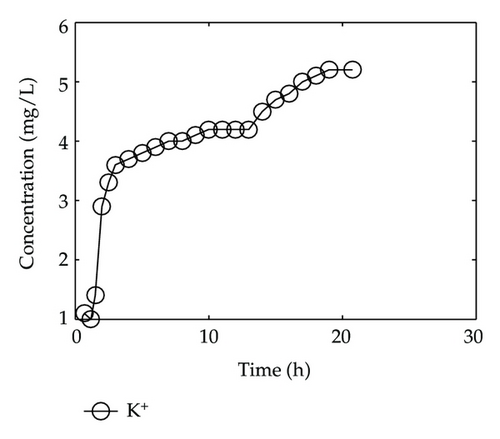
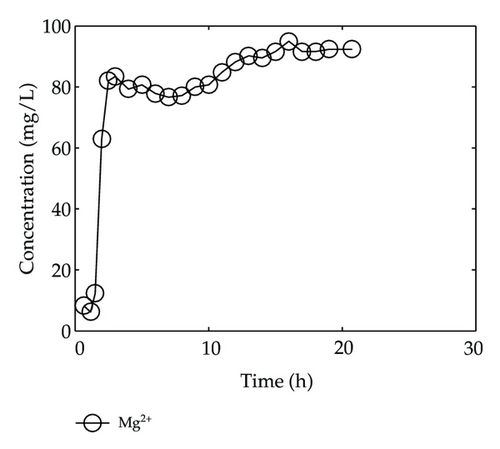
In Figure 1, we find that Ca²⁺, Na⁺, and Mg²⁺ in the liquid phase almost have same behaviors which go up quickly at the initial stage and then tend to steady situations gradually after 2-3 hours; however, there is a different performance for K⁺. Although K⁺ goes up rapidly during the initial stage of 3 hours, it is still in an increasing trend at a slow speed after t = 3 [h].

On the other hand, let us investigate behaviors of negative ions plotted in Figure 2. Cl⁻ and $$ have the same tendency with Ca²⁺, Na⁺, and Mg²⁺, but the situations are complicated for $$ and $$. It is noticeable that the measured initial concentration of $$ in the inflow is very small, and the first sample (at t = 2/3 [h]) gives a high concentration which is 152.7 [mg/L]. The reason may be ascribed to the actions of free CO₂ in the inflow. From t = 2/3 [h] to t = 2 [h], the concentration goes down rapidly, it goes up quickly from t = 2 [h] to t = 6 [h], and approaches to an equilibrium after t = 6 [h]. As for $$, its first breakthrough concentration at t = 2/3 [h] is 1.4 [mg/L], which is lower than that of 1.7 [mg/L] in the inflow, and after t = 2/3 [h], it goes up rapidly during t ∈ (2/3,3/2) [h], and then goes down rapidly until t = 3 [h]. It is surprising that it still goes down after t = 3 [h] but with small oscillations.

In the following, on the basis of the above analysis, two kinds of mathematical models describing the solutes transport behaviors in the column will be given respectively, and an optimal perturbation algorithm will be introduced to determine the unknown parameters in the models.

3. Mathematical Model and Inversion Algorithm

4. Inversion Results

Following the methods as used in paper [14, 15], we will implement the above optimal perturbation regularization algorithm to determine the unknown vector r given by (3.10) numerically, and then reconstruct the measured breakthrough data for the ions of $$, $$, K⁺, and $$, respectively. The reaction coefficient can be determined in different approximate space, and one needs to choose a suitable approximate dimension N so as to reconstruct the measured data with high accuracy. For the four kinds of ions, we will realize the inversion with different dimension. All computations are performed in a PC of Dell Dimension 9200.

4.1. Data Reconstruction for $$

Set N = 7 and choose regularization parameter as α = 0.08, initial iteration as r₀ = (0,0, 0,0, 0,0, 1), and numerical differential steps vector as τ = (1e − 1,1e − 2, …, 1e − 9), then by 100 iterations which cost CPU time 295.4 [s], we obtain the inversion parameters given as follows:

$$ (4.1)

that is,

$$ (4.2)

$$ (4.3)

and the relative inversion error is worked out as

$$ (4.4)

where η is the measured breakthrough data vector of $$ given in (3.15), and C₂(1, T; r^inv) is the reconstruction data. Furthermore, the inversion reconstruction data and the real measured breakthrough data are plotted in Figure 3.

4.2. Data Reconstruction for $$

Let us consider the solute ion of $$. As for (3.1) with corresponding initial boundary conditions, there is only one initial parameter m₁ to be determined. Therefore, the optimal perturbation algorithm can be simplified as done in paper [14]. By utilizing the optimal perturbation algorithm without regularization term (choosing regularization parameter α = 0), and taking initial iteration value as 1, numerical differential step as τ = 1e − 1, the initial index can be determined by 7 iterations costing CPU time 1.7 [s] which is m₁ = 3.7588, and the relative inversion error is Err = 0.0277. Figure 4 plots the measured breakthrough data and the reconstructed data of $$, respectively.

4.3. Data Reconstruction for $$

As for K⁺, similarly as done for $$, take N = 3 here and choose regularization parameter as α = 0.05, initial iteration as r₀ = (0,0, 0,0, 1), and numerical differential steps vector as τ = (1e − 2,1e − 3,1e − 4,1e − 5,1e − 6), the unknown reaction coefficient, and the initial index for K⁺ are worked out by 31 iterations which costing CPU time 24.0 [s] given as follows:

$$ (4.5)

and the relative inversion error is Err = 0.0141. Figure 5 plots the measured breakthrough data and the reconstructed data of K⁺, respectively.

Now let us deal with data reconstruction for $$ in which case the situation seems to be a little complicated. If still following the above method, there are no inversion results we need to appear. So, we perform the algorithm in a little different way as compared with the above computations by choosing a fixed initial index prescribed. Moreover, if setting an initial index in advance, then we only need to determine the time-dependent reaction coefficient.

On the concrete computations, taking m₄ = 3, N = 9, regularization parameter as α = 0.05, initial iteration as zero, and numerical differential steps vector as τ = (1e − 1,1e − 2, …, 1e − 10), an optimal reaction coefficient for $$ is worked out by 500 iterations which costing CPU time 1636.7 [s] given as follows:

$$ (4.6)

and the relative inversion error is Err = 0.0285. The measured breakthrough data and the reconstruction data for $$ are plotted in Figure 6, respectively.

5. Discussions and Conclusions

5.1. Discussions

5.1.1. On Reaction Coefficient

Firstly, let us investigate actions of the reaction coefficients. By the inversion result (4.2) for $$, and noting (3.2) (i = 2) and its dimensionless form (3.5), we can get

$$ (5.1)

which is the reaction coefficient with dimensional time t for $$. By (5.1) we can see that the expansion coefficients of β₁(t) become smaller and smaller as N goes to large.

Similarly, the reaction coefficients β₂(t) and β₃(t) in (3.2) (i = 2,3) can be worked out which are given as

$$ (5.2)

respectively. Furthermore, β_i(t) (i = 1, 2, 3) are plotted in Figure 7 so as to study their changes with the experimental time, respectively.

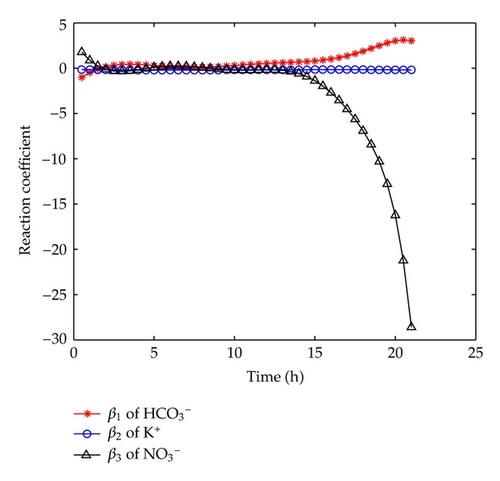
From Figure 7, we can find that the reaction to K⁺ almost has no change throughout the experiment; and the reaction to $$ goes up at the initial stage, and then keeps a little increase during t ∈ (5,15)[h]. As for the reaction to $$, it decreases during the initial stage, and then keeps unchanging during t ∈ (2,15)[h], and after t > 15 [h], it becomes decreasing quickly.

It is noticeable that the above arguments basically coincide with those hydrochemical analysis given in Section 2 except for $$ in the case of t > 15 [h]. In addition, we also find that β₂(t) and β₃(t) both have similar asymptotic properties as β₁(t), that is, the expansion coefficients of the reaction term go to zero as N becomes large.

5.1.2. On Space Distribution at the First Outflow

Now, look at the following figure which plots space distributions at the first outflow time of T = T₀ for the four kinds of solute ions.

From Figure 8, we can see that at the first outflow time of t = 2/3 [h], $$, $$, and K⁺ are in similar situations, and $$ has a special behavior.

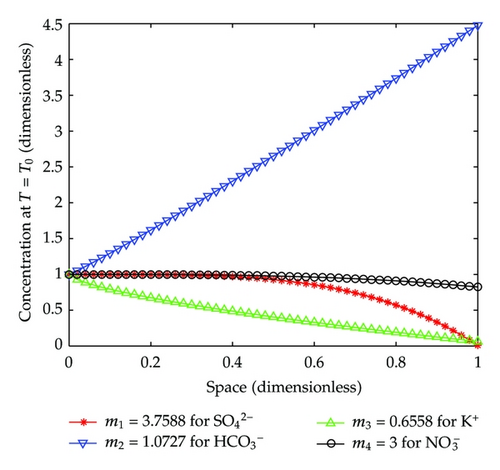
For $$, its concentration varies from 1 (t = 0) to 1.4/1.7 ≈ 0.8235 (t = 2/3 [h]), and goes down almost along with a straight line very slowly.

For $$, its concentration varies from 1 (t = 0) to 10.0/1023.2 ≈ 0.0098 (t = 2/3 [h]), and goes down with convexity but faster than $$.

For K⁺, its concentration varies from 1 (t = 0) to 1.1/17.2 ≈ 0.0640 (t = 2/3 [h]), and decreases also faster than $$, but with concavity.

As for $$, its concentration changes from 1 (t = 0) to 152.7/34.1 ≈ 4.4780 (t = 2/3 [h]), and goes up quickly with almost linearity.

In summary, during this interval of t ∈ (0,2/3)[h], hydrodynamical advection dispersion actions may be play dominating roles in the solutes transport through the column. However, there are some chemical reactions occurring in $$ except for mechanical advection and dispersion. For example, the free CO₂ in the inflow can produce $$ when penetrating through the column, and the amount of $$ reaches a maximum at the bottom of the column at t = 2/3 [h].